Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Форум, библиотека и блог: mathprofi

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

2. Дискретный вариационный ряд.
Полигон частот и эмпирическая функция распределения

На вводном уроке по математической статистике мы узнали, что такое математическая статистика, и теперь обо всём подробнее. Далее для удобства я буду нумеровать статьи и постараюсь делать их не слишком длинными. Потому что всё действительно просто, и главное, здесь научиться рациональной технике вычислений, на которую и будет сделан особый упор.

Интервальные и дискретные вариационные ряды почти сразу же встретились в предыдущей статье, и мы начинаем с дискретного случая, когда количественная эмпирическая величина  может принимать лишь отдельные изолированные значения.

…что-то не понятно по терминам? Срочно изучать первый урок! (ссылка выше)

Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант  (значений величины ) и соответствующих им частот либо относительных частот.

Частоты выборочной совокупности обозначают через , частоты генеральной совокупности – через . И сразу разбираемся с новым термином. Относительные частоты рассчитываются по формулам:

, где  – объем выборки, при этом, сумма всех относительных частот: .

Аналогично для совокупности генеральной:
, где  – её объем, и, очевидно:

И тут вспоминается Пример 2 об оценках по матанализу в группе из  студентов:

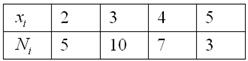
– пожалуйста, пример дискретного вариационного ряда, где варианты  – это оценки, а частоты  – количество студентов, получивших ту или иную оценку.

Для разминки найдём относительные частоты:

и непременно проконтролируем, что: .

Все вычисления обычно проводят на калькуляторе либо в Экселе, а результаты заносят в таблицу, при этом, в статистике данные чаще располагают не в строках, а в столбцах:

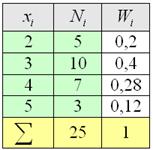
Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в строчку. Не редкость, когда их 10-20, а бывает, и 100-200, что тоже и неоднократно встречалось в моей практике. И это не какие-то супер-пупер расчёты, а учебные задачи!

После сей позитивной новости продолжаем :)

Откуда берутся дискретные вариационные ряды? Такие ряды появляются в результате учёта дискретной характеристики статистической совокупности, причём, варианты ряда не отличаются большим разнообразием. Например, оценки (коих не так много) в примере выше.

И сейчас мы примем непосредственное участие в этом процессе:

Пример 4

По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3. Требуется:

– составить вариационный ряд и построить полигон частот;
– найти относительные частоты и построить эмпирическую функцию распределения.

Чего томиться? – вся тема урока в одной задаче!

Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. В данном случае это легко сделать устно: .

Квалификационные разряды – есть величина дискретная, и поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).

Как это сделать?

Если у вас под рукой нет вычислительных программ, то вручную (Эксель разберём ниже). При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка:

и делать около соответствующих кружков засечки:

После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке:

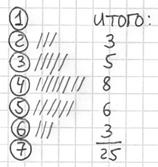
И обязательно проверяем, получается ли у нас в сумме объём выборки :
, отлично, искомый ряд составлен, заносим полученные значения в таблицу на чистовик:

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяют достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)

Построенный вариационный ряд также называют статистическим распределением выборки, причём, этот термин применИм не только для дискретного, но и для интервального ряда, который мы рассмотрим на следующем уроке.

Построим полигон частот. Это статистический аналог многоугольника распределения дискретной случайной величины (кто изучал). Полигон частот – это ломаная, соединяющая соседние точки :

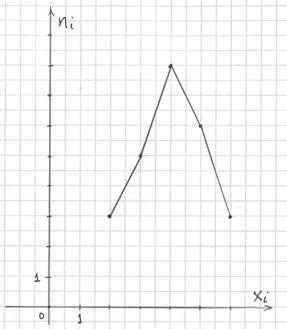
…эх, ностальгия. Но, пятилетку-другую, думается, так решать ещё будут.

Теперь современный способ:

Задание 1

Самостоятельно решить данную задачу в Экселе (прямо в открывшемся файле).

Решаем! – исходные данные с пошаговой инструкцией прилагаются.

Вторая часть задачи. Найдём относительные частоты , для этого каждую частоту  делим на  и результат заносим в дополнительный столбец, далее я перехожу к электронной версии:

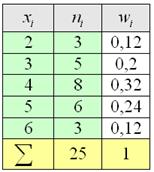
– обязательно проверяем, что сумма относительных частот равна единице!

Иногда требуется построить полигон относительных частот. Как вы правильно догадываетесь – это ломаная, соединяющая соседние точки . Но такое задание больше характерно для интервального вариационного ряда.

А теперь посмотрим на относительные частоты и задумаемся, на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что  – есть примерная вероятность того, что наугад выбранный рабочий цеха будет иметь 4-й разряд. «Примерная» – по той причине, что перед нами выборка.

А вот если учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты  – и есть в точности эти вероятности.

Построим эмпирическую функцию распределения . Это статистический аналог функции распределения из тервера. Данная функция определяется, как отношение:

, где  – количество вариант СТРОГО МЕНЬШИХ, чем ,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.

И процесс пошёл:

Очевидно, что на интервале , и, кроме того, функция равна нулю ещё и в точке . Почему? Потому, что значение  определяет количество вариант, которые СТРОГО меньше двух, а это количество равно нулю.

На промежутке  – и опять обратите внимание, что значение  не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх.

На промежутке   и далее процесс продолжается по принципу накопления частот:

– если , то ;

– если , то ;

– и, наконец, если , то  – и в самом деле, для ЛЮБОГО «икс» из интервала  ВСЕ частоты расположены СТРОГО левее этого «икс».

Накопленные относительные частоты удобно записывать в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева 1-е значение (красная стрелка), а каждое следующее получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения):

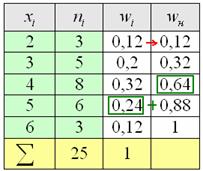
Вот, кстати, ещё один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.

Саму функцию принято записывать в кусочном виде:

а её график представляет собой ступенчатую фигуру:

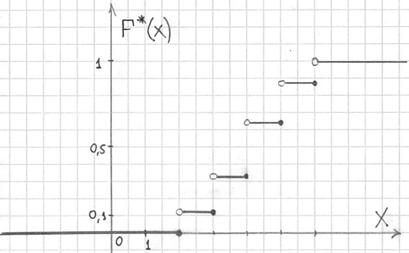
Эмпирическая функция распределения не убывает  и принимает значения из промежутка , и если у вас вдруг получится не так, то ищите ошибку.

И сейчас мы автоматизируем процесс; видео, к сожалению, не вписалось по ширине, посему смотрим его на Ютубе:

  Как построить эмпирическую функцию распределения?

Эмпирическая функция распределения  строится по выборке и приближает теоретическую функцию распределения . Легко догадаться, что последняя образуется на основании исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на небе – уже вряд ли. Вот поэтому и важнА именно эмпирическая функция, и ещё важнее, чтобы выборка была репрезентативна, дабы приближение было хорошим.

Миниатюрная задача для закрепления материала:

Пример 5

Дано статистическое распределение выборки

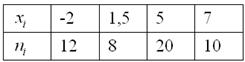
Составить эмпирическую функцию распределения, выполнить чертёж

Задание 2

Самостоятельно решить Пример 5 в Экселе, все числа и обозначения уже там.

Свериться с образцом можно ниже. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.

И я жду вас на третьем уроке, где речь пойдёт об интервальном вариационном ряде.

Решения и ответы:

Пример 5. Решение: заполним расчётную таблицу:

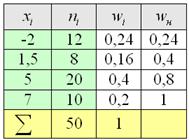
Составим эмпирическую функцию распределения:

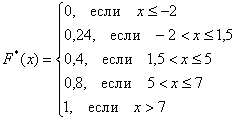
Выполним чертёж:

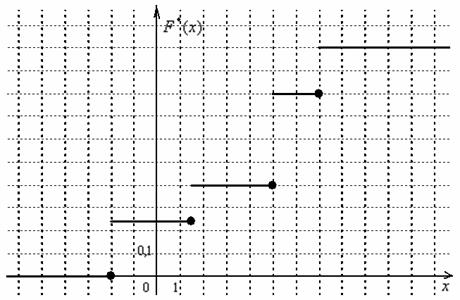
Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

© Copyright mathprofi.ru, Александр Емелин, 2010-2024. Копирование материалов сайта запрещено