Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Форум, библиотека и блог: mathprofi

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

6. Формула для вычисления дисперсии.
Среднее квадратическое отклонение. Коэффициент вариации

В первой части урока мы рассмотрели размах вариации, среднее линейное отклонение и дисперсию, и продолжение темы в заголовке. Многие из этих показателей фигурируют в теории вероятностей, и если вы зашли с поисковика именно за ними, то сразу ссылка на нужную статью: Дисперсия дискретной случайной величины – там же всё остальное.

Ну а здесь на повестке дня Математическая статистика (организационный урок для «чайников»), и мы продолжаем изучать показатели вариации:

• Формула для вычисления дисперсии
• Среднее квадратическое отклонение, которое также называют среднеквадратическим или стандартным отклонением. Тут же исправленное среднее квадратическое отклонение.
• Коэффициент вариации

Всё с формулами, примерами решений и техникой рациональных вычислений.

И снова о дисперсии.

На предыдущем занятии мы рассчитывали дисперсию по определению:
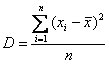 – для несгруппированных данных и
 – для дискретного либо интервального вариационного ряда.

Если известно, генеральная ли нам дана совокупность или выборочная, то хорошим тоном считается поставить подстрочные индексы:  либо .

Расчёт дисперсии по определению прост и реально используется на практике, но существует ещё более простой и удобный способ вычисления – по формуле, которую несложно вывести из определения:

 – дисперсия равна разности средней арифметической квадратов всех вариант статистической совокупности и квадрата средней самих этих вариант.

ОСМЫСЛЕННО повторяем ВСЛУХ и вникаем! … Карл украл у Клары кораллы, а Клара украла у Карла кларнет :)

Если что-то не очень понятно, то сейчас всё станет на свои места:

Для несгруппированных вариант  выборочной совокупности формула детализируется следующим образом:

и для готового вариационного ряда – так:
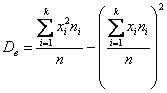, где  – кратные (одинаковые) варианты дискретного ряда либо середины интервалов интервального ряда, а  – соответствующие частоты.

Для генеральной дисперсии  формулы те же, только с буквами  вместо . Во многих случаях удобно использовать просто значок суммирования  – без переменной-«счётчика», поскольку в контексте той или иной задачи и так понятно, что суммируется.

И начнём мы со знакомой подопытной задачи:

Пример 15

В результате 10 независимых измерений получены опытные данные, которые представлены в таблице:

Это данные из Примера 13, и на этот раз нам требуется вычислить дисперсию с помощью формулы. Напоминаю, что там мы её рассчитали по определению и получили результат , таким образом, ответ известен заранее, и это всегда круто. Всегда, когда он правильный.

Решение: используем формулу .
Для этого нужно найти выборочную среднюю, повторим действие: ,
вычислить квадраты всех вариант:

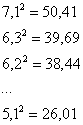
и их сумму:
Результаты вычислений удобно заносить в таблицу:

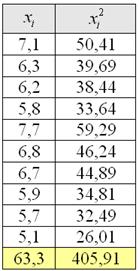
Осталось применить формулу:
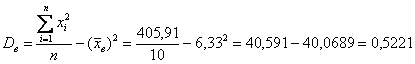, что и требовалось увидеть.

Ответ:

Теперь случай сформированного вариационного ряда. В Примере 14 мы потренировались на дискретном ряде, и сейчас очередь интервального:

Пример 16

С целью изучения вкладов в Сбербанке города проведено выборочное исследование, в результате которого получены следующие данные:

Вычислить выборочную дисперсию и среднее квадратическое отклонение, оценить соответствующие показатели генеральной совокупности.

Автор задачи заботливо подсчитал объем выборки , но не «закрыл» крайние интервалы. Такая вещь уже встречалась, и решение мы начинаем с этого закрытия. Поскольку длины внутренних интервалов составляют  д.е., то логично рассмотреть такую же длину и по краям, то бишь, интервалы от 200 до 400 и от 1000 до 1200 денежных единиц.

…Возможно, у вас возник вопрос, а как быть, если даны интервалы разной длины? В этом случае принимаем за «эталон» среднюю длину известных интервалов.

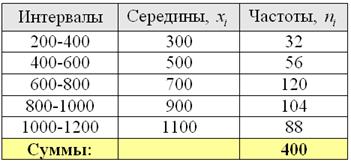
Для расчёта числовых характеристик перейдём к дискретному вариационному ряду, выбрав в качестве вариант  середины интервалов, которые здесь видны устно:

В тяжёлых случаях суммируем концы интервалов и делим их пополам, например: .

Кроме того, варианты целесообразно уменьшить в 1000 раз, поскольку в ходе дальнейших вычислений будут получаться гигантские числа. С современными вычислительными мощностями, это, конечно, не проблема, но смотреться будет некрасиво.

Сначала вычислим выборочную среднюю. Этот алгоритм уже обкатан: находим произведения , их сумму:

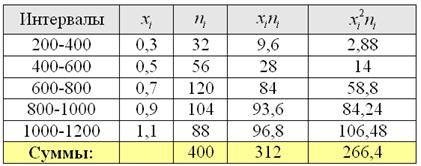
и по соответствующей формуле:
 тыс. д.е. или 780 д.е. – средний размер вклада.

Примечание: далее для компактной записи я буду использовать просто значок  – без переменной-«счётчика».

Теперь дисперсия. Её никто не запрещает рассчитать по определению , но заметьте, насколько легче формула  – для её применения всего-то лишь нужно рассчитать произведения  и их сумму  (правый столбец таблицы). Несмотря на то, что многие читатели уже освоили технику вычислений в Экселе, я продолжу записывать ролики – мало ли, кто что запамятовал:

Итак, по формуле вычисления дисперсии, получаем:
 тыс. д.е. в квадрате (т.к. по определению, дисперсия – есть величина квадратичная).

И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь квадратный корень:
 тыс. д.е. или 240 денежных единиц. Полученный показатель называется

среднее квадратическое отклонение

Или стандартное отклонение. Оно обозначается греческой буквой «сигма», и коль скоро у нас выборочная совокупность, то добавляем соответствующий подстрочный индекс:

 – выборочное среднее квадратическое отклонение.

Чем меньше стандартное отклонение (и дисперсия), тем меньше вариация – тем бОльшее количество вариант находится вблизи выборочной средней. Но у нас, как нетрудно «прикинуть на глазок», разброс довольно-таки велик – значительное количество вкладов расположено далековато от , и поэтому значение  получилось немалым.

Следующая часть задачи состоит в том, чтобы корректно оценить генеральную дисперсию  и генеральное среднее квадратическое отклонение .

В 1-й части урока я рассказал о том, что выборочная дисперсия  представляет собой смещённую оценку генеральной дисперсии. Это означает, что если мы будем проводить неоднократные выборки из той же генеральной совокупности, то полученные значения  будут систематически занижено оценивать . Обращаю ваше внимание, что это не значит, что  будет всегда меньше, чем .

И поэтому выборочную дисперсию, как намекает условие, нужно поправить:
 – исправленная выборочная дисперсия

и, соответственно:
 или 240,30 д.е. – исправленное среднее квадратическое отклонение.

 и  – это уже несмещённые оценки генеральной дисперсии  и генерального стандартного отклонения  соответственно.

Ввиду большого объёма выборки (более 100 вариант) этой поправкой можно пренебречь, но всё же мы не будем «разбрасываться» 30 «копейками».

Ответ: ; в качестве оценки соответствующих генеральных показателей принимаем  и .

Рассмотренные выше показатели (размах вариации, среднее линейное отклонение, дисперсия, стандартное отклонение) входят в группу абсолютных показателей вариации, которые обладают рядом неудобств. Так, если в прорешанной задаче не уменьшать варианты в 1000 раз, то дисперсия получится в миллион раз больше! Да-да, не , а . И возникает естественное желание привести результаты к некому единому стандарту.

Для этого существуют показатели относительные, и самым известным из них является

коэффициент вариации

– это отношение стандартного отклонения к средней, выраженное в процентах:

И вот теперь совершенно без разницы, в д.е. мы считали:

или в тысячах д.е.:

Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .

В статистике существует следующий эмпирический ориентир:

– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение  хорошо характеризует центральную тенденцию совокупности.

– если показатель вариации составляет существенно больше 30%, то совокупность неоднородна, то есть, значительное количество вариант находятся далеко от , и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть квартили, децили, а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.

Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей :)

Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.

И сейчас, конечно же, задачки для самостоятельного решения:

Пример 17, на отработку терминов и формул:

а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.

б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.

и Пример 18, творческий:

Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:

Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.

Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!

Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов.

Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке :)

Задание 8

Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.

Краткое решение и ответ в конце урока, который подошёл к концу.

Следующее занятие не за горами, а уже за кочкой:

Асимметрия и эксцесс эмпирического распределения

Решения и ответы:

Пример 17. Решение:

а) Используем формулу . По условию, , . Таким образом:

б) Используем формулу . По условию, , . Таким образом:

Ответ: а) , б)

Пример 18. Решение: вычислим сумму вариант и сумму их квадратов:

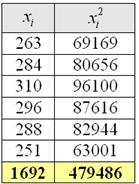
Найдём среднюю:
 тонны – среднемесячный объем производства за полугодие.
Дисперсию вычислим по формуле:

Среднее квадратическое отклонение:
 тонн.
Коэффициент вариации:

Ответ:  тонны,  тонн,

Краткие выводы: за первое полугодие среднемесячный объём производства труб составил  тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

© Copyright mathprofi.ru, Александр Емелин, 2010-2024. Копирование материалов сайта запрещено