Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Геометрическое распределение вероятностей

И геометрия тут ни при чём. Это один из особых видов распределения дискретной случайной величины, которое получается в следующей ситуации:

Пусть проводится серия испытаний, в каждом из которых случайное событие  может появиться с вероятностью ; причём, испытания заканчиваются при первом же появлении данного события. Тогда случайная величина , характеризующая количество совершённых попыток, как раз и имеет геометрическое распределение.

Рассмотрим, например, такое событие:  – при подбрасывании монеты выпадет орёл.

Начинаем подбрасывать монету. Совершенно понятно, что вероятность появления орла в любом испытании равна , и наша задача заключается в том, чтобы проанализировать – как скоро появится первый орёл (после чего серия закончится). Составим закон распределения случайной величины  – количества проведённых бросков.

Если , то это означает, что орёл выпал в первой же попытке. Вероятность этого события равна:

Если , то в первой попытке выпала решка (вероятность ), а во второй – орёл. По теореме умножения вероятностей зависимых событий:

Если , то в первых двух испытаниях появились решки, а в третьем – орёл. По той же теореме:

Если , то первый орёл появился лишь в четвёртом испытании:

…сколько же можно подбрасывать монету?  Теоретически – до бесконечности :)

И перед нами пример дискретной случайной величины, которая  принимает бесконечное и счётное количество значений. В общем виде её закон распределения записывается следующим образом:

Вероятности  представляют собой бесконечно убывающую геометрическую прогрессию с первым членом  и основанием . Отсюда и название – геометрическое распределение вероятностей. Как известно, сумма такой прогрессии равна:

, что полностью соответствует вероятностному смыслу задачи.

Однако жизнь такова, что всё когда-то заканчивается, и поэтому в практических задачах количество испытаний почти всегда ограничивается. На «грубую» такое распределение тоже можно считать геометрическим и сейчас мы разберём классический пример:

Задача

Стрелок производит несколько выстрелов в цель до первого попадания, имея всего 4 патрона. Вероятность попадания при одном выстреле равна 0,6. Найти закон распределения случайной величины , математическое ожидание , дисперсию , где  – количество произведённых выстрелов. Построить многоугольник и функцию распределения данной случайной величины. Найти .

…если встретилось много непонятных слов, то начните со статьи Случайные величины.

Решение: по условию, вероятность попадания в каждом испытании равна . Тогда вероятность промаха: .

Составим закон распределения случайной величины :

1)  
Это означает, что стрелок попал с 1-й попытки и на этом испытания закончились:

2)  – в первом испытании промах, во втором – попадание. По теореме умножения вероятностей зависимых событий:

3)  – попадание с третьей попытки:

И, наконец:

4)  

Здесь стрелок может промахнуться или попасть, но испытания заканчиваются в любом случае. Вместе с патронами. По теоремам умножения вероятностей зависимых и сложения несовместных событий:

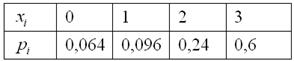
Таким образом, искомый закон распределения:

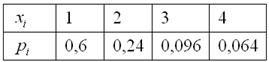
Обязательно выполняем проверку:
, что и требовалось проверить.

Построим многоугольник распределения:

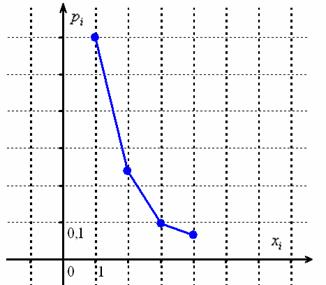
Вычислим  и . Для геометрического распределения существуют специальные формулы нахождения математического ожидания и дисперсии: , но нам ими воспользоваться не удастся – по той причине, что количество испытаний не бесконечно. Поэтому придётся использовать общий алгоритм. Заполним расчётную таблицу:

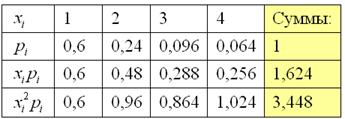
Математическое ожидание лежит готовенькое:   – это среднеожидаемое количество выстрелов (при многократном повторении таких серий из 4 выстрелов).

Дисперсию вычислим по формуле:
 – это мера рассеяния количества выстрелов относительно математического ожидания.

Очевидно, что чем ниже квалификация стрелка (значение ), тем больше будут эти значения. И, наоборот – с увеличением  матожидание приближается к единице, а дисперсия к нулю, ибо снайпер в подавляющем большинстве случаев выбивает цель с первой попытки да с малой погрешностью относительно «центра мишени».

Этот факт хорошо виден из теоретических формул для бесконечного количества выстрелов. Давайте, кстати, ради интереса вычислим:

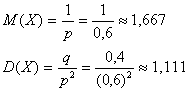
Ну что же, значения нашей «реальной» задачи весьма близкИ к этим результатам.

Составим функцию распределения вероятностей:

Выполним чертёж:

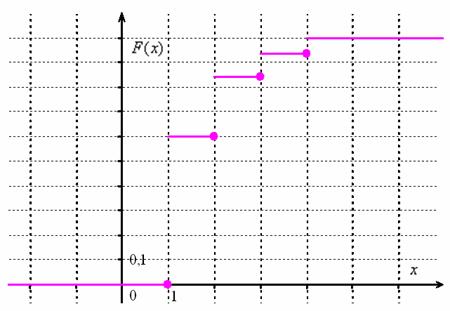
Найдём  – вероятность того, что значение случайной величины отклонится от математического ожидания не более чем на .

Сначала вычислим среднее квадратическое отклонение:

затем – требуемую вероятность:

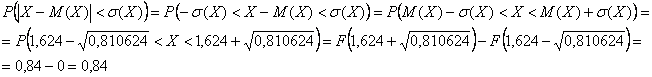
напоминаю, что на интервале  концентрируются «основные события», и поэтому такой высокий результат неудивителен.

Готово!

Но при всей кажущейся простоте, у этого задания существуют подводные камни. Главное коварство состоит в том, условие может быть сформулировано по такому же шаблону, но случайная величина быть ДРУГОЙ. Например:

 – количество промахов.

В этом случае закон распределения вероятностей примет следующий вид:

Здесь  – вероятность того, что будет 3 промаха (в 4-й попытке попадание);  – вероятность того, что стрелок совершит 4 промаха.

Естественно, что все числовые характеристики и содержательный выводы будут другими, однако сам закон распределения сохранит свой «геометрический» характер.

Вот ещё одна хитрая вариация, которая мне встречалась на практике:

 – количество неизрасходованных патронов.

Закон распределения этой величины таков:

Проанализируйте данный случай самостоятельно.

Кстати, в примере, который мы прорешали, случайную величину  можно эквивалентно сформулировать, как «количество израсходованных патронов».

Но и это ещё не всё – случайная величина может вообще иметь другой вид распределения!

Таким образом, к решению подобных задач нельзя подходить формально – во избежание ошибок, ВСЕГДА ДУМАЙТЕ ГОЛОВОЙ, анализируйте реалистичность полученных результатов. И тогда математическое ожидание  в разобранной задаче вас явно насторожит :)

Дополнительные примеры по теме, в том числе весьма творческие, можно найти в решебнике по теме. Далее рекомендую изучить биномиальное, пуассоновское и гипергеометрическое распределения вероятностей.

Желаю успехов!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте