
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Квадратичные формы.
Знакоопределённость форм. Критерий Сильвестра
Прилагательное «квадратичный» сразу наталкивает на мысль, что что-то здесь связано с квадратом (второй степенью), и очень скоро мы узнаем это «что-то» и что такое форма. Прямо скороговоркой получилась :)
Приветствую вас на своём новом уроке, и в качестве незамедлительной разминки мы рассмотрим форму в полосочку линейную. Линейной формой ![]() переменных называют однородный многочлен 1-й степени:
переменных называют однородный многочлен 1-й степени:
![]() , где:
, где:
![]() – какие-то конкретные числа* (предполагаем, что хотя бы одно из них отлично от нуля), а
– какие-то конкретные числа* (предполагаем, что хотя бы одно из них отлично от нуля), а ![]() – переменные, которые могут принимать произвольные значения.
– переменные, которые могут принимать произвольные значения.
* В рамках данной темы будем рассматривать только действительные числа.
С термином «однородный» мы уже сталкивались на уроке об однородных системах линейных уравнений, и в данном случае он подразумевает, что у многочлена нет приплюсованной константы ![]() .
.
Например: ![]() – линейная форма двух переменных
– линейная форма двух переменных
Теперь форма квадратичная. Квадратичной формой ![]() переменных называют однородный многочлен 2-й степени, каждое слагаемое которого содержит либо квадрат переменной, либо парное произведение переменных. Так, например, квадратичная форма двух переменных
переменных называют однородный многочлен 2-й степени, каждое слагаемое которого содержит либо квадрат переменной, либо парное произведение переменных. Так, например, квадратичная форма двух переменных ![]() имеет следующий вид:
имеет следующий вид:
![]()
Внимание! Это стандартная запись, и что-то менять в ней не нужно! Несмотря на «страшный» вид, тут всё просто – двойные подстрочные индексы констант сигнализируют о том, какие переменные входят в то или иное слагаемое:
![]() – в этом слагаемом находится произведение
– в этом слагаемом находится произведение ![]() и
и ![]() (квадрат);
(квадрат);
![]() – здесь произведение
– здесь произведение ![]() ;
;
![]() – и здесь произведение
– и здесь произведение ![]() .
.
Далее будем полагать, что хотя бы одна из констант не равна нулю, и вот, пожалуйста, «неполный» пример: ![]() , в котором:
, в котором:
![]() – сразу упреждаю грубую ошибку, когда теряют «минус» у коэффициента, не понимая, что он относится к слагаемому:
– сразу упреждаю грубую ошибку, когда теряют «минус» у коэффициента, не понимая, что он относится к слагаемому: ![]()
Иногда встречается «школьный» вариант оформления в духе ![]() , но то лишь иногда. Кстати, заметьте, что константы
, но то лишь иногда. Кстати, заметьте, что константы ![]() нам тут вообще ни о чем не говорят, и поэтому запомнить «лёгкую запись» труднее. Особенно, когда переменных больше.
нам тут вообще ни о чем не говорят, и поэтому запомнить «лёгкую запись» труднее. Особенно, когда переменных больше.
И квадратичная форма трёх переменных содержит уже шесть членов:
![]()
…почему в «смешанных» слагаемых ставятся множители-«двойки»? Это удобно, и скоро станет понятно, почему.
Далее ситуация начинает усугубляться:
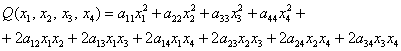
и усугублять мы её дальше не будем, т.к. формы с бОльшим количеством переменных встречаются довольно редко.
Однако общую формулу запишем, её удобно оформить «простынёй»:
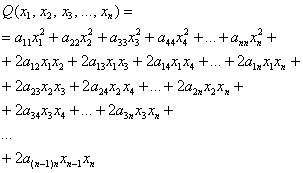
– внимательно изучаем каждую строчку – ничего страшного тут нет!
Квадратичная форма содержит ![]() слагаемых с квадратами переменных и
слагаемых с квадратами переменных и ![]() слагаемых с их парными произведениями (см. комбинаторную формулу сочетаний). Больше ничего – никаких «одиноких иксов» и никакой приплюсованной константы (тогда уже получится не квадратичная форма, а неоднородный многочлен 2-й степени).
слагаемых с их парными произведениями (см. комбинаторную формулу сочетаний). Больше ничего – никаких «одиноких иксов» и никакой приплюсованной константы (тогда уже получится не квадратичная форма, а неоднородный многочлен 2-й степени).
Матричная запись квадратичной формы
Как насчёт матриц? :) Знаю, знаю, соскучились. В практических задачах широко распространенная матричная запись квадратичных форм. Объяснения опять начну с формы линейной, например, от трёх переменных: ![]() . Её можно записать, как произведение двух матриц:
. Её можно записать, как произведение двух матриц:
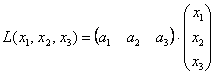
И действительно, выполняя матричное умножение, получаем матрицу «один на один»: 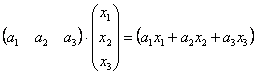 , единственный элемент которой можно эквивалентно записать вне матрицы:
, единственный элемент которой можно эквивалентно записать вне матрицы: ![]() .
.
Легко понять, что линейная форма «эн» переменных записывается в виде:

Квадратичная форма представима в виде произведения уже трёх матриц:
![]() , где:
, где:
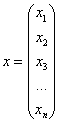 – столбец переменных;
– столбец переменных;
![]() – его транспонированная строка;
– его транспонированная строка;
 – матрица квадратичной формы.
– матрица квадратичной формы.
Это так называемая симметрическая матрица, на главной диагонали которой расположены коэффициенты ![]() при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например,
при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например, ![]() – в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке).
– в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке).
Определитель ![]() называют дискриминантом квадратичной формы, а ранг матрицы
называют дискриминантом квадратичной формы, а ранг матрицы ![]() – рангом квадратичной формы.
– рангом квадратичной формы.
Если перемножить три матрицы ![]() , то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае
, то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае ![]() . Согласно общей формуле, матричная запись данной формы имеет следующий вид:
. Согласно общей формуле, матричная запись данной формы имеет следующий вид:
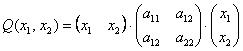
И в самом деле:
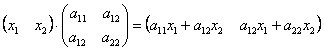
далее:
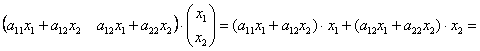
![]() , в чём и требовалось убедиться.
, в чём и требовалось убедиться.
Как вариант, сначала можно было перемножить правые матрицы, и затем первую матрицу умножить на полученный результат.
Вам понравилось так же, как и мне? Ну тогда пример для самостоятельного решения =)
Пример 1
Записать квадратичную форму в матричном виде и выполнить проверку. Определить дискриминант и ранг формы.
![]()
…что-то смущает? ;) Краткое решение и ответ в конце урока! Статьи об определителе и ранге матрицы – в помощь.
После чего разберём аналогичную задачу с формой трёх переменных:
Пример 2
Записать матрицу квадратичной формы, найти её ранг и дискриминант
![]()
Решение: сбросим тяжёлую ношу лишних формул, и будем ориентироваться на сами члены:
– слагаемое ![]() дважды содержит 1-ю переменную, поэтому
дважды содержит 1-ю переменную, поэтому ![]() ;
;
– из аналогичных соображений определяем ![]() и сразу записываем результаты на главную диагональ симметрической матрицы:
и сразу записываем результаты на главную диагональ симметрической матрицы: 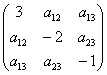 .
.
Так как в слагаемое ![]() входят 1-я и 2-я переменная, то
входят 1-я и 2-я переменная, то ![]() (не забываем поделить на 2) и данный коэффициент занимает свои законные места:
(не забываем поделить на 2) и данный коэффициент занимает свои законные места: 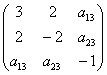 .
.
Поскольку в форме отсутствует член с произведением ![]() (а точнее, присутствует с нулевым множителем:
(а точнее, присутствует с нулевым множителем: ![]() ), то
), то ![]() , и на холст отправляются два нуля:
, и на холст отправляются два нуля: 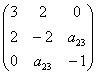 .
.
И, наконец, из слагаемого ![]() определяем
определяем ![]() , после чего картина завершена:
, после чего картина завершена:
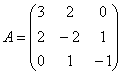 – матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений»
– матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений» ![]() , но и заставили их работать на себя!
, но и заставили их работать на себя!
По условию не требовалось записывать матричное уравнение, однако науки ради:
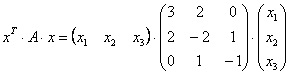
Желающие могут перемножить три матрицы, в результате чего должна получиться исходная квадратичная форма.
Теперь определим ранг формы. Он равен рангу матрицы ![]() . Так как в матрице есть хотя бы один ненулевой элемент, например,
. Так как в матрице есть хотя бы один ненулевой элемент, например, ![]() , то ранг не меньше единицы. Теперь вычислим минор
, то ранг не меньше единицы. Теперь вычислим минор ![]() , значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке:
, значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке:
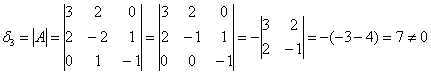 , значит,
, значит, ![]()
Если не очень понятно, что к чему, обязательно изучите статью о ранге матрицы – это довольно замысловатая задачка, и перед нами оказался лишь простой случай, когда угловые миноры не равны нулю.
Дискриминант квадратичной формы получен автоматом.
Ответ:  , ранг равен трём, дискриминант
, ранг равен трём, дискриминант ![]()
Следующее задание для самостоятельного решения:
Пример 3
Восстановить квадратичную форму по её матрице

При этом не нужно вспоминать никаких формул! Решение почти устное:
– сначала смотрим на главную диагональ и записываем слагаемые с квадратами переменных;
– затем анализируем симметричные элементы 1-й строки (или 1-го столбца), и записываем все слагаемые, в которые входит 1-я переменная (не забывая удвоить коэффициенты);
– далее смотрим на оставшиеся симметричные элементы 2-й строки (справа от диагонали) либо 2-го столбца (ниже диагонали) и записываем соответствующие парные произведения (с удвоенными коэффициентами!).
– и, наконец, анализируем правую нижнюю пару симметричных чисел.
Подробное решение и ответ в конце урока.
Знакоопределённость квадратичной формы. Критерий Сильвестра
До сих пор мы рассматривали «внешнее устройство» форм и пришло время изучить их функциональное назначение. Да, по существу, они работают, как функции. Вернёмся к простенькой линейной форме ![]() .
.
Как отмечалось в начале урока, переменные ![]() могут принимать произвольные действительные значения (мы ограничились ими), и каждой такой паре соответствует определённое значение
могут принимать произвольные действительные значения (мы ограничились ими), и каждой такой паре соответствует определённое значение ![]() , например:
, например:
![]()
![]() , и так далее.
, и так далее.
Говоря языком науки, перед нами скалярная функция векторного аргумента, в которой каждому вектору 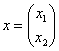 ставится в соответствие определённое число
ставится в соответствие определённое число ![]() . Обращаю ваше внимание, что сейчас идёт речь не о геометрическом векторе, а о векторе в его алгебраическом понимании.
. Обращаю ваше внимание, что сейчас идёт речь не о геометрическом векторе, а о векторе в его алгебраическом понимании.
В зависимости от значений ![]() рассматриваемая форма может принимать как положительные, так и отрицательные значения, и то же самое касается любой линейной формы
рассматриваемая форма может принимать как положительные, так и отрицательные значения, и то же самое касается любой линейной формы ![]() – если хотя бы один из её коэффициентов отличен от нуля, то она может оказаться как положительной, так и отрицательной (в зависимости от значений
– если хотя бы один из её коэффициентов отличен от нуля, то она может оказаться как положительной, так и отрицательной (в зависимости от значений ![]() ).
).
Такая форма называется знакопеременной. И если с линейной формой всё прозрачно, то с формой квадратичной дела обстоят куда более интересно:
![]()
Совершенно понятно, что данная форма может принимать значения любого знака, таким образом, квадратичная форма тоже может быть знакопеременной.
А может и не быть:
![]() – всегда, если только
– всегда, если только ![]() одновременно не равны нулю.
одновременно не равны нулю.
![]() – для любого вектора
– для любого вектора 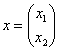 , кроме нулевого
, кроме нулевого ![]() .
.
И вообще, если для любого ненулевого вектора 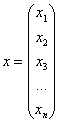 ,
, ![]() , то квадратичную форму называют положительно определённой; если же
, то квадратичную форму называют положительно определённой; если же ![]() – то отрицательно определённой.
– то отрицательно определённой.
И всё бы было хорошо, но определённость квадратичной формы виднА лишь в простых примерах, и эта видимость теряется уже при небольшом усложнении:
![]() – ?
– ?
Можно предположить, что форма определена положительно, но так ли это на самом деле? Вдруг существуют значения ![]() , при которых она меньше нуля?
, при которых она меньше нуля?
На этот счёт существует теорема: если ВСЕ собственные числа матрицы квадратичной формы положительны*, то она определена положительно. Если все отрицательны – то отрицательно.
* В теории доказано, что все собственные числа действительной симметрической матрицы действительны
Запишем матрицу вышеприведённой формы:
![]() и из уравнения
и из уравнения ![]() найдём её собственные значения:
найдём её собственные значения:
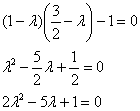
Решаем старое доброе квадратное уравнение:
![]()
![]() , значит, форма
, значит, форма ![]() определена положительно, т.е. при любых ненулевых значениях
определена положительно, т.е. при любых ненулевых значениях ![]() она больше нуля.
она больше нуля.
Рассмотренный метод вроде бы рабочий, но есть одно большое НО. Уже для матрицы «три на три» искать собственные числа – есть занятие долгое и неприятное; с высокой вероятностью получится многочлен 3-й степени с иррациональными корнями.
Как быть? Существует более простой путь!
Критерий Сильвестра
Нет, не Сильвестра Сталлоне :) Сначала напомню, что такое угловые миноры матрицы. Это определители ![]() которые «разрастаются» из её левого верхнего угла:
которые «разрастаются» из её левого верхнего угла:

и последний из них в точности равен определителю матрицы.
Теперь, собственно, критерий:
1) Квадратичная форма определена положительно тогда и только тогда, когда ВСЕ её угловые миноры больше нуля: ![]() .
.
2) Квадратичная форма определена отрицательно тогда и только тогда, когда её угловые миноры знакочередуются, при этом 1-й минор меньше нуля: ![]() ,
, ![]() , если
, если ![]() – чётное или
– чётное или ![]() , если
, если ![]() – нечётное.
– нечётное.
Если в 1-й или 2-й последовательности есть нулевые миноры, то это два особых случая, которые я разберу чуть позже, после того, как мы перещёлкаем более распространённые примеры. При любой другой комбинации плюсов-минусов (и опционально нулей) форма знакопеременна.
Проанализируем угловые миноры матрицы ![]() :
:
![]() , и это сразу говорит нам о том, что форма не определена отрицательно (отпал пункт 2).
, и это сразу говорит нам о том, что форма не определена отрицательно (отпал пункт 2).
![]()
Вывод: все угловые миноры больше нуля, значит, форма ![]() определена положительно.
определена положительно.
Есть разница с методом собственных чисел? ;)
Запишем матрицу формы ![]() из Примера 1:
из Примера 1:
![]()
первый её угловой минор ![]() , а второй
, а второй ![]() , откуда следует, что форма знакопеременна, т.е. в зависимости от значений
, откуда следует, что форма знакопеременна, т.е. в зависимости от значений ![]() , может принимать как положительные, так и отрицательные значения. Впрочем, это и так очевидно.
, может принимать как положительные, так и отрицательные значения. Впрочем, это и так очевидно.
Возьмём форму ![]() и её матрицу из Примера 2:
и её матрицу из Примера 2:

тут вообще без озарения не разобраться. Но с критерием Сильвестра нам всё нипочём:
![]() , следовательно, форма точно не отрицательна.
, следовательно, форма точно не отрицательна.
![]() , и точно не положительна (т.к. все угловые миноры должны быть положительными).
, и точно не положительна (т.к. все угловые миноры должны быть положительными).
Вывод: форма знакопеременна.
Разминочные примеры для самостоятельного решения:
Пример 4
Исследовать квадратичные формы на знакоопределенность
а) ![]()
б) ![]()
В этих примерах всё гладко (см. конец урока), но на самом деле для выполнения такого задания критерия Сильвестра может оказаться не достаточно.
Дело в том, что существуют «краевые» случаи, а именно: если для любого ненулевого вектора ![]() , то форма определена неотрицательно, если
, то форма определена неотрицательно, если ![]() – то неположительно. У этих форм существуют ненулевые векторы
– то неположительно. У этих форм существуют ненулевые векторы 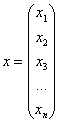 , при которых
, при которых ![]() .
.
Здесь можно привести такой «баян»:
![]()
Выделяя полный квадрат, сразу видим неотрицательность формы: ![]() , причём, она равна нулю и при любом векторе с равными координатами, например:
, причём, она равна нулю и при любом векторе с равными координатами, например: ![]() .
.
«Зеркальный» пример неположительно определённой формы:
![]()
и ещё более тривиальный пример:
![]() – здесь форма равна нулю при любом векторе
– здесь форма равна нулю при любом векторе ![]() , где
, где ![]() – произвольное число.
– произвольное число.
Как выявить неотрицательность или неположительность формы?
Для этого нам потребуется понятие главных миноров матрицы. Главный минор – это минор, составленный из элементов, которые стоят на пересечении строк и столбцов с одинаковыми номерами. Так, у матрицы  существуют два главных минора 1-го порядка:
существуют два главных минора 1-го порядка:
![]() (элемент находится на пересечении 1-й строки и 1-го столбца);
(элемент находится на пересечении 1-й строки и 1-го столбца);
![]() (элемент находится на пересечении 2-й строки и 2-го столбца),
(элемент находится на пересечении 2-й строки и 2-го столбца),
и один главный минор 2-го порядка:
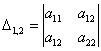 – составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца.
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца.
У матрицы «три на три»  главных миноров семь, и тут уже придётся помахать бицепсами:
главных миноров семь, и тут уже придётся помахать бицепсами:
![]() – три минора 1-го порядка,
– три минора 1-го порядка,
три минора 2-го порядка:
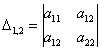 – составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца;
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца;
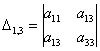 – составлен из элементов 1-й, 3-й строки и 1-го, 3-го столбца;
– составлен из элементов 1-й, 3-й строки и 1-го, 3-го столбца;
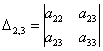 – составлен из элементов 2-й, 3-й строки и 2-го, 3-го столбца,
– составлен из элементов 2-й, 3-й строки и 2-го, 3-го столбца,
и один минор 3-го порядка:
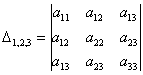 – составлен из элементов 1-й, 2-й, 3-й строки и 1-го, 2-го и 3-го столбца.
– составлен из элементов 1-й, 2-й, 3-й строки и 1-го, 2-го и 3-го столбца.
Задание на понимание: записать все главные миноры матрицы  .
.
Сверяемся в конце урока и продолжаем.
Критерий Шварценеггера:
1) Ненулевая* квадратичная форма определена неотрицательно тогда и только тогда, когда ВСЕ её главные миноры неотрицательны (больше либо равны нулю).
* У нулевой (вырожденной) квадратичной формы все коэффициенты равны нулю.
2) Ненулевая квадратичная форма с матрицей ![]() определена неположительно тогда и только тогда, когда её:
определена неположительно тогда и только тогда, когда её:
– главные миноры 1-го порядка неположительны (меньше либо равны нулю);
– главные миноры 2-го порядка неотрицательны;
– главные миноры 3-го порядка неположительны (пошлО чередование);
…
– главный минор ![]() -го порядка неположителен, если
-го порядка неположителен, если ![]() – нечётное либо неотрицателен, если
– нечётное либо неотрицателен, если ![]() – чётное.
– чётное.
Если хотя бы один минор противоположного знака, то форма знакопеременна.
Посмотрим, как работает критерий в вышеприведённых примерах:
![]()
Составим матрицу ![]() формы, и в первую очередь вычислим угловые миноры – а вдруг она определена положительно или отрицательно?
формы, и в первую очередь вычислим угловые миноры – а вдруг она определена положительно или отрицательно?
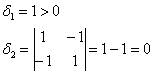
Полученные значения не удовлетворяют критерию Сильвестра, однако второй минор не отрицателен, и это вызывает надобность проверить 2-й критерий (в случае ![]() 2-й критерий будет не выполнен автоматически, т.е. сразу делается вывод о знакопеременности формы).
2-й критерий будет не выполнен автоматически, т.е. сразу делается вывод о знакопеременности формы).
Главные миноры 1-го порядка:
![]() – положительны,
– положительны,
главный минор 2-го порядка:
![]() – не отрицателен.
– не отрицателен.
Таким образом, ВСЕ главные миноры не отрицательны, значит, форма неотрицательна.
Запишем матрицу ![]() формы
формы ![]() , для которой, очевидно, не выполнен критерий Сильвестра. Но и противоположных знаков мы тоже не получили (т.к. оба угловых минора равны нулю). Поэтому проверяем выполнение критерия неотрицательности / неположительности. Главные миноры 1-го порядка:
, для которой, очевидно, не выполнен критерий Сильвестра. Но и противоположных знаков мы тоже не получили (т.к. оба угловых минора равны нулю). Поэтому проверяем выполнение критерия неотрицательности / неположительности. Главные миноры 1-го порядка:
![]() – не положительны,
– не положительны,
главный минор 2-го порядка:
![]() – не отрицателен.
– не отрицателен.
Таким образом, по критерию Шварценеггера (пункт 2), форма определена неположительно.
Теперь во всеоружии разберём более занятную задачку:
Пример 5
Исследовать квадратичную форму на знакоопределенность
![]()
Данную форму украшает орден «альфа», который может равняться любому действительному числу. Но это ж только веселее будет, решаем.
Сначала запишем матрицу формы, наверное, многие уже приноровились это делать устно: на главную диагональ ставим коэффициенты при квадратах, а на симметричные места – споловиненные коэффициенты соответствующих «смешанных» произведений:

Вычислим угловые миноры:
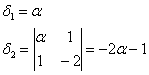
третий определитель я раскрою по 3-й строке:
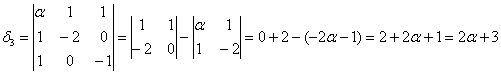
Кстати, в силу симметрии, по 3-му столбцу он раскрывается точно так же.
Дальнейшее решение удобно разбить на 2 пункта:
1) Выясним, существуют ли значения «альфа», при которых форма определена положительно или неотрицательно. Согласно критерию Сильвестра, условию положительности формы соответствует следующая система линейных неравенств:
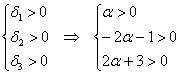
В соответствии с поставленной задачей, сначала разберёмся со 2-м неравенством:
![]()
умножим обе его части на ![]() , сменив у неравенства знак:
, сменив у неравенства знак:
![]() , что противоречит первому неравенству системы.
, что противоречит первому неравенству системы.
Таким образом, система несовместна, а значит, форма не может быть положительно определённой ни при каких «альфа», из чего логически и автоматически следует, что она не может быть и неотрицательной.
2) Проведём исследование на отрицательность / неположительность. По Сильвестру, условию отрицательности формы соответствует следующая система линейных неравенств:
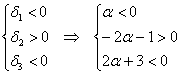
Второе неравенство уже решено: ![]() , и оно не противоречит первому. И третье неравенство тоже «вписалось в рамки»:
, и оно не противоречит первому. И третье неравенство тоже «вписалось в рамки»: ![]() .
.
Таким образом, имеем совместную систему:
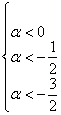
из которой следует, что форма определена отрицательно при ![]() . Например, если
. Например, если ![]() :
:
![]() – то при любом ненулевом векторе
– то при любом ненулевом векторе 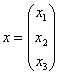 данная форма будет строго отрицательна.
данная форма будет строго отрицательна.
Осталось исследовать «пограничный» случай. Если ![]() , то:
, то:
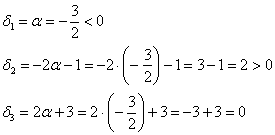
Последнее значение не удовлетворяет 2-му пункту критерия Сильвестра, однако оно равно нулю, что позволяет предположить неположительность формы. Запишем матрицу 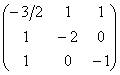 формы и проверим критерий Шварценеггера. Главные миноры первого порядка:
формы и проверим критерий Шварценеггера. Главные миноры первого порядка:
![]() – отлично, все миноры неположительны, поэтому проверка продолжается.
– отлично, все миноры неположительны, поэтому проверка продолжается.
Рассчитываем миноры 2-го порядка. Если хотя бы один из них окажется отрицательным, то форма будет знакопеременной:
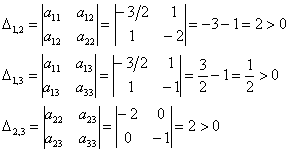
Нет, все миноры неотрицательны, и минор 3-го порядка уже рассчитан:
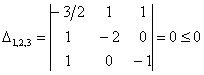
Таким образом, по критерию Шварценеггера (пункт 2), имеет место неположительность формы, иными словами, ![]() , причём, нулю она равна и при некоторых ненулевых значениях
, причём, нулю она равна и при некоторых ненулевых значениях ![]() .
.
Ответ: при ![]() форма определена отрицательно, при
форма определена отрицательно, при ![]() неположительно, в остальных случаях форма знакопеременна.
неположительно, в остальных случаях форма знакопеременна.
И творческое задание для самостоятельного решения:
Пример 5*
Исследовать квадратичную форму на знакоопределенность
![]()
И в заключение статьи хочу выразить благодарность Сергею Хохлову, некогда ст. преподавателю МПГУ – за важные замечания и интересные дополнительные примеры, а также Арнольду Шварценеггеру, который сыграл в непривычном для себя амплуа и помог мне ярче объяснить материал :)
Как сказал актёр, I’ll be back, и я жду вас на следующем уроке – о каноническом виде квадратичной формы.
Решения и ответы:
Пример 1. Решение: сначала приведём подобные слагаемые:
![]()
Квадратичная форма двух переменных имеет вид ![]() , в данном случае:
, в данном случае: ![]() . Запишем форму в матричном виде:
. Запишем форму в матричном виде:
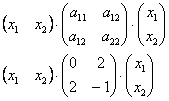
Проверка:

что и требовалось проверить.
Вычислим дискриминант формы:
![]()
Поскольку ![]() , то ранг формы равен двум.
, то ранг формы равен двум.
Ответ: 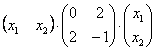 ,
, ![]() , ранг формы равен двум.
, ранг формы равен двум.
Пример 3. Решение: симметрическая матрица 4*4 определяет квадратичную форму 4 переменных. Коэффициенты главной диагонали ![]() , следовательно:
, следовательно:
![]()
Симметричные коэффициенты 1-й строки: ![]() , таким образом:
, таким образом:
![]()
Оставшиеся симметричные элементы 2-й строки: ![]() , и:
, и:
![]()
И, наконец, ![]()
Ответ: ![]()
Пример 4. Решение:
а) запишем матрицу формы:
![]()
и вычислим её угловые миноры:
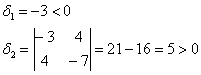
Таким образом, по критерию Сильвестра, форма определена отрицательно.
б) запишем матрицу формы:
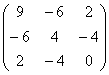
и вычислим её угловые миноры:
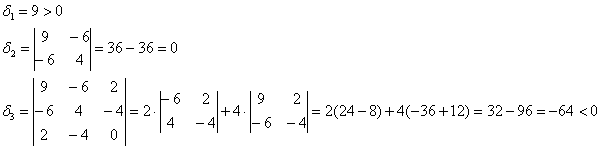
Вывод: форма знакопеременна.
Задание на понимание: у данной матрицы четыре главных минора 1-го порядка:
![]() ,
,
шесть главных миноров 2-го порядка:
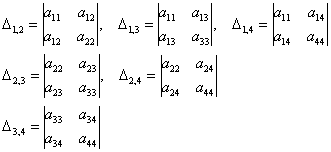
четыре главных минора 3-го порядка:
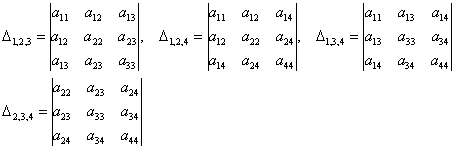
и один главный минор 4-го порядка, равный определителю матрицы.
Пример 5*. Решение: запишем матрицу формы 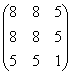 и вычислим её угловые миноры:
и вычислим её угловые миноры:
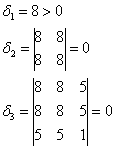
Таким образом, форма не удовлетворяет критерию Сильвестра, однако, может оказаться неотрицательной (т.к. ![]() и остальные миноры нулевые). Для этого все главные миноры должны быть неотрицательны. Главные миноры 1-го порядка:
и остальные миноры нулевые). Для этого все главные миноры должны быть неотрицательны. Главные миноры 1-го порядка:
![]() .
.
Вычислим главные миноры 2-го порядка:
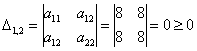
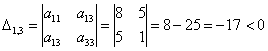 – среди главных миноров встретился отрицательный, следовательно, форма не удовлетворяет критерию неотрицательности.
– среди главных миноров встретился отрицательный, следовательно, форма не удовлетворяет критерию неотрицательности.
Ответ: форма знакопеременна.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
