
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить математическое ожидание и дисперсию
непрерывной случайной величины?
Ответ на этот вопрос состоит всего лишь из 2 слов: с помощью интегралов. Приветствую тех, кто подтянулся с поисковика – вы попали на 2-ю часть урока о непрерывной случайной величине (НСВ), и если что-то будет не понятно, милости прошу по ссылкам.
Сам смысл математического ожидания и дисперсии мы уже разбирали ранее (но, конечно, повторим), и сейчас настало время узнать, как они определяются для НСВ. Всё очень просто: по аналогии с ДСВ. Математическое ожидание непрерывной случайной величины ![]() определяется, как несобственный интеграл:
определяется, как несобственный интеграл:
![]() , где
, где ![]() – функция плотности распределения этой случайной величины.
– функция плотности распределения этой случайной величины.
Примечание: несложный вывод этой формулы можно найти, например, в учебном пособии В.Е. Гмурмана
Дисперсия тоже имеет «знакомые очертания»: ![]() (по определению), но в практических задачах гораздо удобнее применять формулу:
(по определению), но в практических задачах гораздо удобнее применять формулу:
![]()
Как и в случае с дискретной случайной величиной, она не может быть отрицательной!
И среднее квадратическое отклонение вычисляется точно так же:
![]()
Итак, все инструменты в руках и мы с энтузиазмом приступаем к работе учёбе любимому делу:
Пример 7
…нет, это не опечатка – пример уже 7-й!
Непрерывная случайная величина ![]() задана функцией распределения вероятностей:
задана функцией распределения вероятностей:
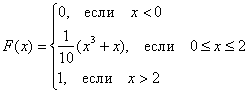
Вычислить ![]() . И построим ещё графики
. И построим ещё графики ![]() и
и ![]() , ну а куда же без них?
, ну а куда же без них?
Решение начнём с графика функции распределения. При его ручном построении удобно найти промежуточное значение ![]() и аккуратно провести кусок кубической параболы
и аккуратно провести кусок кубической параболы ![]() :
:
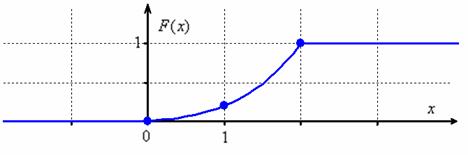
Повторяем: функция распределения ![]() описывает вероятность того, что случайная величина
описывает вероятность того, что случайная величина ![]() примет значение, МЕНЬШЕЕ, чем переменная
примет значение, МЕНЬШЕЕ, чем переменная ![]() , «пробегающая» все значения от
, «пробегающая» все значения от ![]() до
до ![]() . Данная функция изменяется в пределах
. Данная функция изменяется в пределах ![]() и не убывает (т. к. «накапливает» вероятности), а также является непрерывной (для НСВ).
и не убывает (т. к. «накапливает» вероятности), а также является непрерывной (для НСВ).
Очевидно, что случайная величина ![]() принимает случайные значения из отрезка
принимает случайные значения из отрезка ![]() , и какие из них более вероятны, а какие – менее, наглядно показывает функция ПЛОТНОСТИ распределения вероятностей:
, и какие из них более вероятны, а какие – менее, наглядно показывает функция ПЛОТНОСТИ распределения вероятностей:
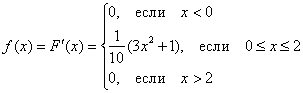
И снова опорные точки: ![]() с немедленным чертёжом:
с немедленным чертёжом:
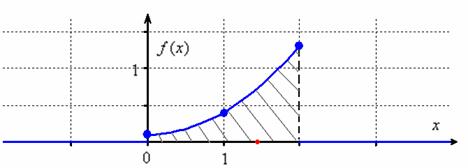
В отличие от ![]() функции плотности может быть разрывна и может принимать значения бОльшие единицы (как в нашем случае); может, как убывать, так и возрастать и даже иметь экстремумы (наш кусок параболы растёт). Однако, она неотрицательна:
функции плотности может быть разрывна и может принимать значения бОльшие единицы (как в нашем случае); может, как убывать, так и возрастать и даже иметь экстремумы (наш кусок параболы растёт). Однако, она неотрицательна: ![]() и обладает свойством
и обладает свойством ![]() , которое лучше всегда проверять (а то мало ли, опечатка или ошибка). В силу аддитивности интеграла:
, которое лучше всегда проверять (а то мало ли, опечатка или ошибка). В силу аддитивности интеграла:
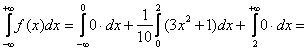
![]() – данный результат равен заштрихованной площади и с вероятностной точки зрения означает тот факт, что случайная величина
– данный результат равен заштрихованной площади и с вероятностной точки зрения означает тот факт, что случайная величина ![]() достоверно примет одно из значений отрезка
достоверно примет одно из значений отрезка ![]() . Причём, по чертежу хорошо видно, что значения из правой части отрезка гораздо более вероятны, чем значения слева.
. Причём, по чертежу хорошо видно, что значения из правой части отрезка гораздо более вероятны, чем значения слева.
И эти вероятности оцениваются кусками площади, а не значениями функции ![]() !!! (окончательно избавляемся от распространённой иллюзии)
!!! (окончательно избавляемся от распространённой иллюзии)
Ради интереса вычислим:
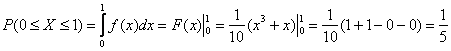 – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение из промежутка
примет значение из промежутка ![]()
Теперь числовые характеристики. Очевидно, что математическое ожидание (среднеожидаемое значение) случайной величины ![]() должно находиться в «живом» отрезке
должно находиться в «живом» отрезке![]() , причём – ближе к его правому концу (поскольку там выше плотность вероятности). Убедимся в этом аналитически. По формуле вычисления математического ожидания, и в силу того же свойства аддитивности:
, причём – ближе к его правому концу (поскольку там выше плотность вероятности). Убедимся в этом аналитически. По формуле вычисления математического ожидания, и в силу того же свойства аддитивности:
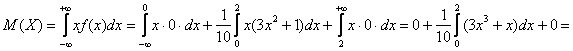
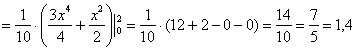 – ну что же, вполне и вполне правдоподобно, результат я отметил красной точкой на чертеже.
– ну что же, вполне и вполне правдоподобно, результат я отметил красной точкой на чертеже.
! Примечание: в общем случае (и в этом, в частности) ![]() не делит площадь на 2 равные части!
не делит площадь на 2 равные части!
Если промежуток конечен, то можно сразу записывать, что матожидание равно определённому интегралу:
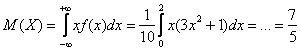
Дисперсию (меру рассеяния случайных значений относительно ![]() ) вычислим по формуле:
) вычислим по формуле:
![]()
Сначала удобно разобраться с интегралом, здесь я не буду расписывать подробно:
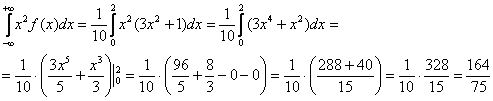
Таким образом:
![]()
И, наконец, среднее квадратическое отклонение:
![]()
Самостоятельно по чертежу оцените, что на интервале ![]() сконцентрирована значительная часть площади – образно говоря, тут находится «гуща событий».
сконцентрирована значительная часть площади – образно говоря, тут находится «гуща событий».
Вот такое вот у нас получилось захватывающее повторение-изучение-исследование!
И коль скоро спрашивалось немного, запишем:
Ответ: ![]()
Строго говоря, ответ следовало записывать и в предыдущих задачах, но когда пунктов много, то итоговые результаты вполне допустимо помечать по ходу решения, например, подчёркивать или обводить карандашом. Однако на моей памяти встречались и строгие рецензенты, которые требовали всё оформлять «по высшему разряду».
Следующее задание для самостоятельного решения:
Пример 8
Дана функция:
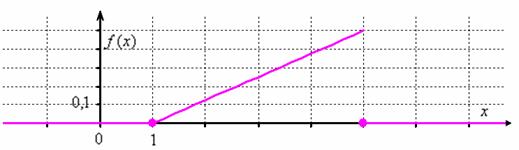
Представить ![]() в аналитическом виде и показать, что она может служить плотностью вероятностей непрерывной случайной величины
в аналитическом виде и показать, что она может служить плотностью вероятностей непрерывной случайной величины ![]() . Вычислить
. Вычислить ![]() и
и ![]() .
.
Да, бывает и так! – вспоминаем уравнение прямой на плоскости. Краткое решение и ответ в конце урока.
Зачастую вычисление математического ожидания и дисперсии сопряжено с техническими трудностями, и заключительные примеры урока будут посвящены их преодолению:
Пример 9
Непрерывная случайная величина ![]() задана функцией плотности распределения
задана функцией плотности распределения 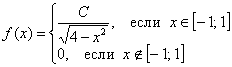 .
.
Найти: ![]() …, прямо так и хочется добавить ещё, но в жуткой борьбе с самим собой я остановился, чтобы сосредоточиться на главном =)
…, прямо так и хочется добавить ещё, но в жуткой борьбе с самим собой я остановился, чтобы сосредоточиться на главном =)
Решение: найдём коэффициент ![]() . Согласно свойству
. Согласно свойству ![]() :
:
![]()
Выносим константу и пользуемся чётностью подынтегральной функции на симметричном промежутке:
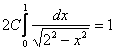
интеграл здесь табличный, и значения арксинуса «хорошие»:
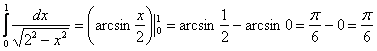
Таким образом:
![]() и функция плотности распределения:
и функция плотности распределения:
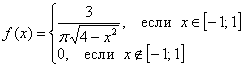
Проверочка: 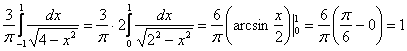 , ч.т.п., и не забываем проконтролировать, что
, ч.т.п., и не забываем проконтролировать, что ![]() .
.
Вычислим математическое ожидание:
![]() , как интеграл от нечётной функции по симметричному промежутку.
, как интеграл от нечётной функции по симметричному промежутку.
Но, в принципе, тут можно не полениться и подвести функцию под знак дифференциала:
![]()
Интересно отметить, что математическое ожидание ![]() «разделило» вероятности (единичную площадь под функцией плотности) на 2 равные части:
«разделило» вероятности (единичную площадь под функцией плотности) на 2 равные части:
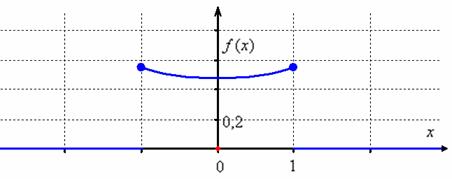
Но, как я примечал выше, в общем случае это не так. Здесь это получилось по причине чётности ![]() и «симметричных» вероятностей. Также обратите внимание на то, что наша функция достигает минимума в точке
и «симметричных» вероятностей. Также обратите внимание на то, что наша функция достигает минимума в точке ![]() и около этого значения сконцентрированы наименее вероятные значения случайной величины. Впрочем, распределение вероятностей близкО к равномерному.
и около этого значения сконцентрированы наименее вероятные значения случайной величины. Впрочем, распределение вероятностей близкО к равномерному.
Поскольку математическое ожидание равно нулю, то дисперсию удобно вычислить «одной строкой». Используем формулу и чётность подынтегральной функции:
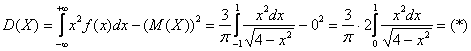
Здесь сразу же удобно провести замену переменной, о которой я рассказывал в Примере 4 урока об эффективных методах решения интегралов:
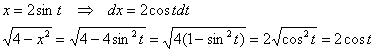
Найдём новые пределы интегрирования. Если ![]() , то
, то ![]() и:
и:
![]()
…мда, хороший вышел каламбур на счёт одной строки :), продолжаем:
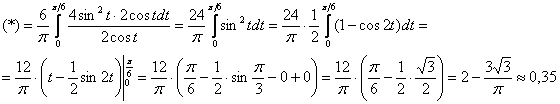
Результат получился положительным, и это уже хороший знак. Тем не менее, не помешает выполнить косвенную проверку и вычислить среднее квадратическое отклонение:
![]() – ну что же, вполне и вполне реалистично, ещё раз взгляните на чертёж и мысленно отмерьте от
– ну что же, вполне и вполне реалистично, ещё раз взгляните на чертёж и мысленно отмерьте от ![]() влево/вправо 0,6.
влево/вправо 0,6.
А вот если бы отклонение вышло равным 1, 2 или бОльшему числу, то это говорило бы о явной ошибке.
Ответ: ![]()
Существует более трудная вариация рассмотренной функции
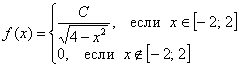
– с двумя вертикальными асимптотами в точках разрыва и сходящимся несобственным интегралом. Такие задачи предлагают даже студентам-заочникам, но я не стал маньячить, и поместил похожий пример в библиотеку для самостоятельного изучения.
Всё хорошо в меру:
Пример 10
Непрерывная случайная величина ![]() задана своей функцией распределения:
задана своей функцией распределения:
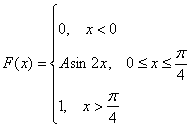
Вычислить математическое ожидание, дисперсию и стандартное отклонение.
Вспоминаем интегрирование по частям, при этом, чтобы не запутаться, лучше придерживаться известного алгоритма: сначала находим неопределенный интеграл, затем проверяем первообразную дифференцированием, и только потом используем формулу Ньютона-Лейбница.
В целях самоконтроля полезно построить график плотности и отложить на чертеже математическое ожидание, затем найти дисперсию и оценить «правдоподобность» стандартного отклонения.
И задача с несобственными интегралами:
Пример 11
Непрерывная случайная величина ![]() задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
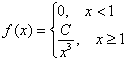
Найти ![]() и
и ![]() . Составить функцию распределения и построить графики
. Составить функцию распределения и построить графики ![]() . Вычислить вероятность того, что случайная величина
. Вычислить вероятность того, что случайная величина ![]() примет значение, бОльшее, чем её математическое ожидание.
примет значение, бОльшее, чем её математическое ожидание.
Нахождение функции распределения как-то так затерялось в последних задачах, и поэтому самое время освежить в памяти формулу ![]() . И, кстати, перед вами пример непрерывной случайной величины с бесконечной дисперсией. Да, так бывает! Но удивляться тут не нужно – потому что бывают и более интересные случаи. …Я знал, что вы соскучились =)
. И, кстати, перед вами пример непрерывной случайной величины с бесконечной дисперсией. Да, так бывает! Но удивляться тут не нужно – потому что бывают и более интересные случаи. …Я знал, что вы соскучились =)
Решения и ответы совсем близко. Для желающих предлагаю более трудное задание с функцией ![]() , где нужно расписать модуль (свериться можно здесь же).
, где нужно расписать модуль (свериться можно здесь же).
И предчувствие вас не обмануло! Точно так же, как и в дискретном случае, у непрерывной случайной величины есть особые виды распределений, самые популярные из которых рассмотрены в следующих статьях:
равномерное распределение;
показательное распределение;
нормальное распределение.
+ тематический pdf-решебник с десятками готовых задач, но это уже когда нагуляете аппетит :)
В добрый путь!
Решения и ответы:
Пример 8. Решение: представим ![]() в аналитическом виде. Составим уравнение прямой по точкам
в аналитическом виде. Составим уравнение прямой по точкам ![]() и
и ![]() :
:
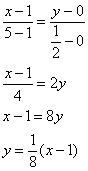
Таким образом:
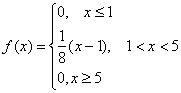
Примечание: верхние неравенства можно записать и так: ![]() , в условии нет однозначной инструкции на этот счёт.
, в условии нет однозначной инструкции на этот счёт.
Покажем, что ![]() может служить плотностью вероятностей НСВ
может служить плотностью вероятностей НСВ ![]() :
:
1) функция ![]() на всей числовой прямой;
на всей числовой прямой;
2) 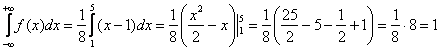
Таким образом, ![]() может служить плотностью вероятностей непрерывной случайной величины
может служить плотностью вероятностей непрерывной случайной величины ![]()
Вычислим математическое ожидание:

Дисперсию вычислим по формуле:
![]()
В данном случае:
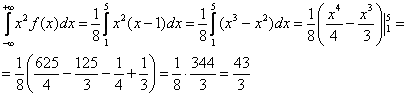
Таким образом:
![]()
Среднее квадратическое отклонение:
![]()
Пример 10. Решение: найдем коэффициент ![]() . В силу непрерывности функции распределения:
. В силу непрерывности функции распределения:
![]()
Таким образом:
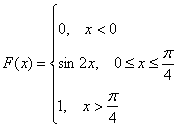
Найдем функцию плотности распределения![]() :
:
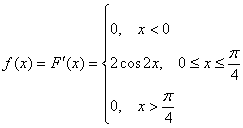
Вычислим математическое ожидание:
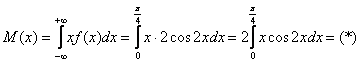
Интегрируем по частям:

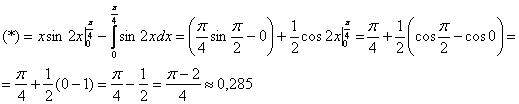
Построим график плотности распределения и отметим на оси математическое ожидание, значение которого получилось весьма правдоподобным:
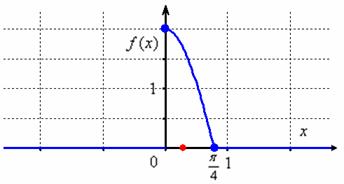
Дисперсию вычислим по формуле:
![]()
В данном случае:
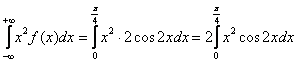
Сначала найдём неопределённый интеграл:
![]()
Дважды интегрируем по частям:
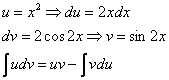
![]()
![]()
![]()
Проверка:
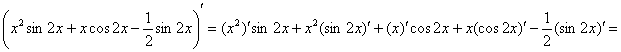
![]() – исходная функция, ч.т.п.
– исходная функция, ч.т.п.
Вычислим определённый интеграл:
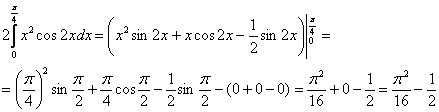
Дисперсия:
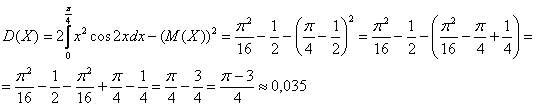
Вычислим среднее квадратическое отклонение:
![]()
По чертежу хорошо видно, что на интервале ![]() сконцентрирована значительная плотность вероятности, что служит косвенным подтверждением правильности вычислений.
сконцентрирована значительная плотность вероятности, что служит косвенным подтверждением правильности вычислений.
Ответ: ![]()
Пример 11. Решение: найдём коэффициент ![]() . Используем свойство
. Используем свойство ![]() .
.
В данном случае:
![]()
Вычислим несобственный интеграл:
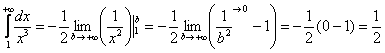
Таким образом:
![]()
и функция плотности распределения:
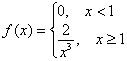
Вычислим математическое ожидание:
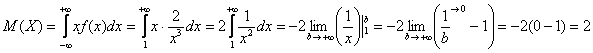
Дисперсию вычислим по формуле:
![]()
в данном случае:
![]() , откуда следует, что
, откуда следует, что ![]() .
.
Функцию распределения вероятностей найдём по формуле ![]() :
:
1) на интервале ![]() и
и ![]() ;
;
2) на промежутке ![]() , следовательно:
, следовательно:
![]()
Таким образом:
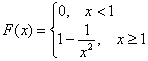
Выполним чертежи:
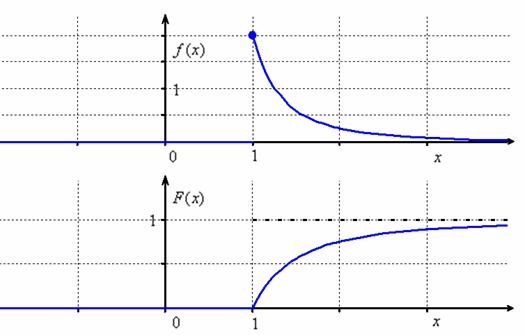
Вычислим ![]()
![]() – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение, бОльшее, чем её математическое ожидание.
примет значение, бОльшее, чем её математическое ожидание.
Примечание: так как случайная величина теоретически может принимать сколь угодно большие значения, то такое смещение ![]() вполне закономерно.
вполне закономерно.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
