
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
10. Оценка генеральной средней и генеральной доли
по повторной и бесповторной выборке
Продолжаем тему статистических оценок, и сразу разбираемся в новых словах, которые следовало бы озвучить ещё на первом уроке :)
Повторная и бесповторная выборка. Что это значит? Слова говорят сами за себя:
– Если случайно отбираемые объекты не возвращаются в генеральную совокупность, то это бесповторная выборка. Если же выбранный объект возвращается обратно (перед выбором следующего), то это повторная выборка, т.е. здесь один и тот же попугай может быть выбран неоднократно.
И те и другие примеры уже встречались ранее, но, конечно, нам привычнее и понятнее бесповторный отбор. Вспоминаем основной метод статистики и Фёдора с помидорами. Совершенно понятно, что после случайного выбора помидора нет никакого смысла возвращать его обратно в коробку, более того, в этом даже есть вредный смысл – ибо овощ может попасться снова, что ухудшит репрезентативность выборки. Или исследование успеваемости студентов ВУЗа. Однозначно и лучше бесповторный отбор. Другой пример, это телефонный опрос, давайте под праздник: «Верите ли вы в Деда Мороза?», как вариант, анкетирование: «да / нет / по праздникам». Здесь тоже вредно спрашивать каждого респондента дважды :), и поэтому опрос проводится без повторов.
Но вот в иных случаях это полезно, например, при статистическом исследовании прогулов в университете. Очевидно, что один и тот же студент может попасть в выборку неоднократно, и было бы неправильно не учитывать его повторные прогулы. Или количество обращений в поликлинику – то же самое, один тот же человек может обратиться несколько раз. Другой распространённый пример – многократное измерение некоторой величины. Теоретически генеральная совокупность бесконечна, и из неё мы «выбираем» несколько значений, которые могут повторяться, причём, не только теоретически, но и практически, по причине округления измерений.
А теперь к теме. На данном уроке мы рассмотрим детализированную задачу о доверительном интервале генеральной средней и о доверительном интервале доли; последняя только что встретилась в предновогодней статье об оценке вероятности биномиального распределения (Пример 29). Детализация состоит в том, что построение доверительного интервала зависит от того, бесповторная была проведена выборка или повторная. Как и прежде, полагаем, что во всех нижеследующих задачах генеральная совокупность распределена нормально, либо её распределение близкО к таковому. Этот факт может быть известен и / или подкреплён статистическими методами.
Для опытных читателей мини-оглавление и быстрая ссылка:
Оценка генеральной средней (заголовок ниже)
Оценка генеральной доли
и для всех – большой и приятный путь:
Оценка генеральной средней
Итак, записываем: пусть из нормально распределенной (или около того) генеральной совокупности объёма ![]() проведена выборка объёма
проведена выборка объёма ![]() и по её результатам найдена выборочная средняя
и по её результатам найдена выборочная средняя ![]() и исправленная выборочная дисперсия
и исправленная выборочная дисперсия ![]() .
.
Тогда доверительный интервал для оценки генеральной средней ![]() имеет вид:
имеет вид:
![]() , где
, где ![]() («дельта») – точность оценки, которую также называют предельной ошибкой репрезентативности выборки.
(«дельта») – точность оценки, которую также называют предельной ошибкой репрезентативности выборки.
Точность оценки рассчитывается как произведение ![]() – коэффициента доверия
– коэффициента доверия ![]() на среднюю ошибку выборки
на среднюю ошибку выборки![]() («мю»). Для бесповторной выборки она составляет
(«мю»). Для бесповторной выборки она составляет 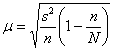 , а для повторной:
, а для повторной: ![]() . В том случае, если изначально известна генеральная дисперсия
. В том случае, если изначально известна генеральная дисперсия ![]() , то используют, конечно, её.
, то используют, конечно, её.
Если объём выборки ![]() , то коэффициент доверия определяется с помощью распределения Стьюдента (см. также Пункт 11б для
, то коэффициент доверия определяется с помощью распределения Стьюдента (см. также Пункт 11б для ![]() ). Если
). Если ![]() , то чаще пользуются соотношением
, то чаще пользуются соотношением ![]() , где
, где ![]() – функция Лапласа, а
– функция Лапласа, а ![]() – доверительная вероятность. Если известна генеральная дисперсия, то второй вариант.
– доверительная вероятность. Если известна генеральная дисперсия, то второй вариант.
Значение «гамма» показывает, с какой вероятностью построенный интервал ![]() накрывает истинное значение
накрывает истинное значение ![]() .
.
С конспектом отмучились, теперь задачи :) Есть у меня тут на выбор несколько штук: про вклады в банке, про токарей на заводе, …но, вот, пожалуй, самая зимняя – как говорится, у кого подснежники в марте, а у кого и подсолнухи в декабре:)
Пример 30
С целью изучения урожайности подсолнечника в колхозах области проведено 5%-ное выборочное обследование 100 га посевов, отобранных в случайном порядке, в результате которого получены следующие данные:
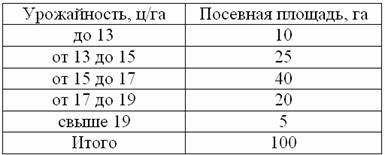
С вероятностью 0,9973 определить предельную ошибку выборки и возможные границы, в которых ожидается средняя урожайность подсолнечника в области.
Решение: в условии не указан тип отбора, но исходя из логики исследования, положим, что он бесповторный. Поскольку выборка 5%-ная, то она составляет 1/20-ю часть генеральной совокупности, стало быть, общая посевная площадь области составляет:
![]() гектаров – не знаю, насколько это реалистично, оставим этот вопрос на совести автора задачи.
гектаров – не знаю, насколько это реалистично, оставим этот вопрос на совести автора задачи.
По условию, требуется найти предельную ошибку выборки ![]() , где
, где ![]() – коэффициент доверия, соответствующий доверительной вероятности
– коэффициент доверия, соответствующий доверительной вероятности ![]() , и коль скоро выборка бесповторна и генеральной дисперсии мы не знаем, то средняя ошибка рассчитывается по формуле
, и коль скоро выборка бесповторна и генеральной дисперсии мы не знаем, то средняя ошибка рассчитывается по формуле 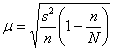 . Далее нужно найти интервал
. Далее нужно найти интервал ![]() , который с вероятностью 99,73% накроет генеральную среднюю
, который с вероятностью 99,73% накроет генеральную среднюю ![]() урожайность подсолнечника по области.
урожайность подсолнечника по области.
И если с коэффициентом «тэ» трудностей никаких, то коэффициент «мю» здесь трудовой – по той причине, что нам не известна ни сама выборочная средняя, ни исправленная выборочная дисперсия. Ну что же, хороший повод освежить пройденный материал.
Смотрим на таблицу выше и приходим к выводу, что нам предложен интервальный вариационный ряд с открытыми крайними интервалами. Поскольку длина частичного интервала составляет ![]() га, то вопрос закрываем так: 11-13 и 19-21 га.
га, то вопрос закрываем так: 11-13 и 19-21 га.
Находим середины ![]() интервалов (переходим к дискретному ряду), произведения
интервалов (переходим к дискретному ряду), произведения ![]() и их суммы:
и их суммы:
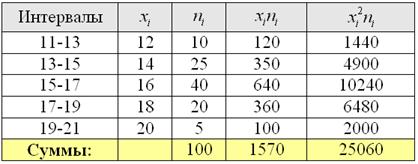
С порядком заполнения таблицы и техникой вычислений можно ознакомиться на предыдущих уроках, даже кино на эту тему есть.
Вычислим выборочную среднюю:
![]() – центнеров с гектара.
– центнеров с гектара.
Выборочную дисперсию вычислим по формуле:
![]()
Этим частенько пренебрегают, но я призываю поправлять дисперсию:
![]() – мелочь, а приятно.
– мелочь, а приятно.
И составляем доверительный интервал ![]() для оценки генеральной средней урожайности подсолнечника по области.
для оценки генеральной средней урожайности подсолнечника по области.
Вычислим предельную ошибку ![]() .
.
Так как объём выборки ![]() , то коэффициент доверия ищем из соотношения
, то коэффициент доверия ищем из соотношения ![]() (но можно использовать и распределение Стьюдента). Поскольку
(но можно использовать и распределение Стьюдента). Поскольку ![]() , то:
, то:
![]()
По таблице значений функции Лапласа или с помощью Экселя (Пункт 5*), определяем, что этому значению функции соотвествует аргумент ![]() .
.
Вычислим среднюю ошибку бесповторной выборки:
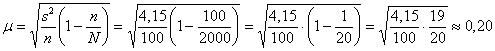 ц/га, таким образом, предельная ошибка составляет
ц/га, таким образом, предельная ошибка составляет ![]() ц/га, и искомый доверительный интервал:
ц/га, и искомый доверительный интервал:
![]()
![]() (ц/га) – границы, в которых ожидается средняя урожайность подсолнечника в области с вероятностью
(ц/га) – границы, в которых ожидается средняя урожайность подсолнечника в области с вероятностью ![]() .
.
Кстати, такое «странное» значение вероятности не случайно, дело в том, что оно соотвествует правилу «трёх сигм», т.е., практически достоверным является тот факт, что построенный интервал накроет истинное значение ![]() средней урожайности по области.
средней урожайности по области.
Ответ: ![]() ц/га,
ц/га, ![]() (ц/га)
(ц/га)
Теперь распишем интервал в развёрнутом виде:
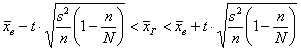
и проанализируем дробь ![]() . Очевидно, что при увеличении объёма выборки
. Очевидно, что при увеличении объёма выборки ![]() эта дробь будут увеличиваться до единицы, и, соответственно, разность
эта дробь будут увеличиваться до единицы, и, соответственно, разность ![]() будет уменьшаться до нуля. Таким образом, предельная ошибка
будет уменьшаться до нуля. Таким образом, предельная ошибка 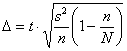 уменьшается, и доверительный интервал становится меньше, что вполне логично – ведь чем больше выборка, тем точнее оценка. И в предельном случае, когда мы исследовали всю генеральную совокупность
уменьшается, и доверительный интервал становится меньше, что вполне логично – ведь чем больше выборка, тем точнее оценка. И в предельном случае, когда мы исследовали всю генеральную совокупность ![]() , ошибка
, ошибка ![]() становится нулевой и доверительный интервал вырождается в генеральную среднюю
становится нулевой и доверительный интервал вырождается в генеральную среднюю ![]() .
.
Исходя из вышесказанного, можно рассмотреть две обратные задачи:
1) Предположим, что нам хочется уменьшить доверительный интервал, например, в два раза, т.е. споловинить предельную ошибку до ![]() ц/га (вместо 0,6). Но высокую доверительную вероятность и соответствующий коэффициент
ц/га (вместо 0,6). Но высокую доверительную вероятность и соответствующий коэффициент ![]() мы сохранить хотим. Тогда ничего не остаётся, как увеличивать объём выборки. Из соотношения
мы сохранить хотим. Тогда ничего не остаётся, как увеличивать объём выборки. Из соотношения 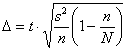 выведем формулу для нахождения этого объёма, для этого возведём обе части в квадрат:
выведем формулу для нахождения этого объёма, для этого возведём обе части в квадрат:
![]() и разрешим уравнение относительно
и разрешим уравнение относительно ![]() :
:
![]() , откуда следует:
, откуда следует:
![]()
Таким образом, для того чтобы с доверительной вероятностью ![]() обеспечить точность
обеспечить точность ![]() , следует организовать выборку объёмом:
, следует организовать выборку объёмом:
![]()
![]() гектара – округляем в бОльшую сторону, что составляет
гектара – округляем в бОльшую сторону, что составляет ![]() генеральной совокупности. Таким образом, трудозатраты возросли примерно в 3,5 раза. Тоже логично.
генеральной совокупности. Таким образом, трудозатраты возросли примерно в 3,5 раза. Тоже логично.
И обращаю ОСОБОЕ внимание, что найденный ранее интервал ![]() уменьшать в два раза НЕЛЬЗЯ:
уменьшать в два раза НЕЛЬЗЯ: ![]() . Почему? Потому что в новой выборке мы почти наверняка получим другое значение
. Почему? Потому что в новой выборке мы почти наверняка получим другое значение ![]() и интервал
и интервал ![]() «сдвинется», да и точность
«сдвинется», да и точность ![]() будет выдержана лишь примерно (т.к. значение
будет выдержана лишь примерно (т.к. значение ![]() тоже изменится).
тоже изменится).
Примечание: некоторые читатели вполне справедливо замечают, что использовать исправленную выборочную дисперсию – не есть хорошо, но за неимением лучшего сойдёт и она. Полученные результаты, разумеется, менее точнЫ, по сравнению с теми, которые получились бы, если бы мы знали генеральную дисперсию.
2) Теперь обратная ситуация – когда оценка ![]() нас устраивают, но нет возможности или времени проводить большую выборку. Да чего тут, исследовали
нас устраивают, но нет возможности или времени проводить большую выборку. Да чего тут, исследовали ![]() гектаров из
гектаров из ![]() , и нормально. В этом случае пострадает доверительная вероятность, давайте выясним насколько:
, и нормально. В этом случае пострадает доверительная вероятность, давайте выясним насколько:
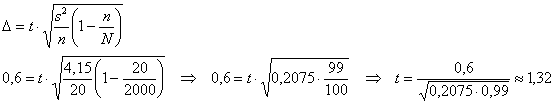
и с помощью расчётного макета (Пункт 10а) для количества степеней свободы ![]() находим соответствующую доверительную вероятность:
находим соответствующую доверительную вероятность:
![]() , что, конечно, «на гране фола».
, что, конечно, «на гране фола».
Впрочем, это было очевидно – ведь такая малая выборка явно не репрезентативна (плохо представляет генеральную совокупность).
Поэтому нужно найти возможность, время, желание и провести нормальное исследование :) А также решить следующую задачу:
Пример 31
По результатам 10%-ной бесповторной выборки объёма ![]() , найдены выборочная средняя
, найдены выборочная средняя ![]() и дисперсия
и дисперсия ![]() .
.
а) Найти пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение генеральной совокупности.
б) Выборку примерно какого объёма нужно организовать, чтобы с той же доверительной вероятностью улучшить точность оценки в три раза?
В пункте «бэ» можно использовать готовую формулу (см. выше), хотя я и противник такого подхода, но во многих источниках предлагается именно она.
Краткое решение и ответ в конце урока.
Если выборка повторная, то почти всё то же самое, с той поправкой, что средняя ошибка выборки определяется без множителя ![]() :
:
![]() , таким образом, предельная ошибка составляет
, таким образом, предельная ошибка составляет ![]() и соответствующий доверительный интервал для оценки генеральной средней:
и соответствующий доверительный интервал для оценки генеральной средней:
![]() – не что иное, как интервал, который был рассмотрен и неоднократно построен в 1-й части урока о статистических оценках.
– не что иное, как интервал, который был рассмотрен и неоднократно построен в 1-й части урока о статистических оценках.
Примечание: если известна дисперсия генеральной совокупности ![]() , то, разумеется, используется она.
, то, разумеется, используется она.
Теперь поставим предельные ошибки рядом:
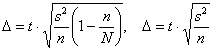
и проанализируем такой момент: при большом объёме ![]() генеральной совокупности (которая может быть и бесконечной) и малом объёма выборки
генеральной совокупности (которая может быть и бесконечной) и малом объёма выборки ![]() грань между формулами стирается. По той причине, что дробь
грань между формулами стирается. По той причине, что дробь ![]() стремится к нулю и разность
стремится к нулю и разность ![]() – к единице, в результате чего 1-я формула практически совпадает со 2-й, чем мы уже пользовались ранее. Вспомним, например, Пример 21:
– к единице, в результате чего 1-я формула практически совпадает со 2-й, чем мы уже пользовались ранее. Вспомним, например, Пример 21:
“
Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением ![]() . Найти доверительный интервал для оценки математического ожидания
. Найти доверительный интервал для оценки математического ожидания ![]() с надежностью 0,95, если выборочная средняя
с надежностью 0,95, если выборочная средняя ![]() , а объем выборки
, а объем выборки ![]() .
.
”
В условии не сказано, повторная ли проведена выборка или бесповторная, и не известен объём ![]() генеральной совокупности. Поэтому ничего не остаётся, как допустить, что она очень великА и пользоваться формулой
генеральной совокупности. Поэтому ничего не остаётся, как допустить, что она очень великА и пользоваться формулой ![]() . В том решении мы получили
. В том решении мы получили ![]() и доверительный интервал
и доверительный интервал ![]() , который с вероятностью
, который с вероятностью ![]() накрывает неизвестное математическое ожидание
накрывает неизвестное математическое ожидание ![]() . Кроме того, было прорешано ещё несколько похожих задач, но во всех из них остался за кадром анализ объёма выборки. И сейчас пришло время наверстать упущенное:
. Кроме того, было прорешано ещё несколько похожих задач, но во всех из них остался за кадром анализ объёма выборки. И сейчас пришло время наверстать упущенное:
Пример 32
По данным Примера 21 (![]() ) определить объём выборки, обеспечивающий точность
) определить объём выборки, обеспечивающий точность ![]() с вероятностью
с вероятностью ![]() .
.
Да, вот так вот сурово :)
Но решение очень простое. Прежде всего, из формулы ![]() выразим «эн», здесь это намного проще. Возведём обе части в квадрат:
выразим «эн», здесь это намного проще. Возведём обе части в квадрат:
![]() и порядок:
и порядок: ![]()
Доверительной вероятности ![]() соответствует коэффициент
соответствует коэффициент ![]() (из соотношения
(из соотношения ![]() ).
).
Таким образом:
![]() – объём выборки, необходимый для обеспечения точности
– объём выборки, необходимый для обеспечения точности ![]() с вероятностью
с вероятностью ![]() .
.
Это означает, что доверительный интервал ![]() , где
, где ![]() – значение, найденное по выборке объёмом 900, практически достоверно накроет генеральную среднюю
– значение, найденное по выборке объёмом 900, практически достоверно накроет генеральную среднюю ![]() .
.
И ещё раз подчёркиваю, что значение ![]() из Примера 21 использовать нельзя, ибо новая выборка – новая средняя. Но заметьте, что здесь известна генеральная дисперсия и поэтому точность
из Примера 21 использовать нельзя, ибо новая выборка – новая средняя. Но заметьте, что здесь известна генеральная дисперсия и поэтому точность ![]() будет выдержана строго.
будет выдержана строго.
Ответ: ![]()
Как видите, объём заметно возрос, и если вам хочется совсем крутой точности, скажем, ![]() с той же вероятностью
с той же вероятностью ![]() , то придётся выбрать уже:
, то придётся выбрать уже:
![]() объектов, после чего практически достоверно можно утверждать, что рассчитанное по этой выборке значение
объектов, после чего практически достоверно можно утверждать, что рассчитанное по этой выборке значение ![]() будет отличаться от
будет отличаться от ![]() менее чем на 0,1. Но тут нужно смотреть – будет ли такая большая выборка целесообразной.
менее чем на 0,1. Но тут нужно смотреть – будет ли такая большая выборка целесообразной.
И в заключение параграфа ещё один любопытный факт: если для бесповторной выборки ошибка 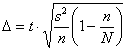 может строго равняться нуля (когда
может строго равняться нуля (когда ![]() ), то для повторной выборки это не так:
), то для повторной выборки это не так: ![]() – здесь она может лишь стремиться к нулю при
– здесь она может лишь стремиться к нулю при ![]() , даже если объём генеральной совокупности конечен. Это обусловлено эффектом повторности – представьте, что из чёрного ящика наугад извлекаются некие предметы и возвращаются обратно. Мало того, что они будут учтены не одинаковое количество раз, так некоторые из них теоретически могут вообще не попадаться сколь угодно долго.
, даже если объём генеральной совокупности конечен. Это обусловлено эффектом повторности – представьте, что из чёрного ящика наугад извлекаются некие предметы и возвращаются обратно. Мало того, что они будут учтены не одинаковое количество раз, так некоторые из них теоретически могут вообще не попадаться сколь угодно долго.
Оценка генеральной доли
Быстренько освежим в памяти, что такое доля. Пусть из генеральной совокупности объёма ![]() вновь проведена выборка объёмом
вновь проведена выборка объёмом ![]() , и по её результатам требуется оценить генеральную долю объектов, обладающих некоторым количественным или качественным признаком.
, и по её результатам требуется оценить генеральную долю объектов, обладающих некоторым количественным или качественным признаком.
Вспоминаем ![]() помидоров на базе, среди которых
помидоров на базе, среди которых ![]() первосортных. Тогда отношение
первосортных. Тогда отношение ![]() является генеральной долей первосортных помидоров. Однако исследовать все овощи затруднительно, поэтому организуется представительная выборка из
является генеральной долей первосортных помидоров. Однако исследовать все овощи затруднительно, поэтому организуется представительная выборка из ![]() помидоров, среди которых первосортных окажется
помидоров, среди которых первосортных окажется ![]() штук. Отношение
штук. Отношение ![]() называется выборочной долей.
называется выборочной долей.
И наша задача состоит в том, чтобы по найденному значению ![]() оценить истинную долю
оценить истинную долю ![]() . Как оценить? С помощью доверительного интервала:
. Как оценить? С помощью доверительного интервала:
![]() , где
, где ![]() – предельная ошибка доли.
– предельная ошибка доли.
Далее для удобства я буду опускать подстрочный индекс у выборочной доли: ![]() .
.
В том случае, если выборка достаточно велика (![]() порядка сотни и больше), а доля не слишком малА (по крайне мере, больше нескольких процентов), то предельная ошибка доли определяется как произведение
порядка сотни и больше), а доля не слишком малА (по крайне мере, больше нескольких процентов), то предельная ошибка доли определяется как произведение ![]() , где
, где ![]() – коэффициент доверия, определяемый из того же соотношения
– коэффициент доверия, определяемый из того же соотношения ![]() для заданного уровня доверительной вероятности, а
для заданного уровня доверительной вероятности, а ![]() – средняя ошибка доли, которая определяется так:
– средняя ошибка доли, которая определяется так:
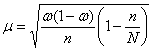 – для бесповторной выборки;
– для бесповторной выборки;
![]() – для повторной выборки.
– для повторной выборки.
В том случае, если генеральная совокупность велика, а выборка малА, то для бесповторной выборки можно использовать и 2-ю формулу, ибо дробь ![]() будет близка к нулю.
будет близка к нулю.
Как видите, формулы очень похожи, только вместо дисперсии у нас тут произведение ![]() , и чего томиться, сразу задача:
, и чего томиться, сразу задача:
Пример 33
В целях изучения суточного пробега автомобилей автотранспортного предприятия проведено 10%-ное выборочное обследование 100 автомобилей методом случайного бесповторного отбора, в результате которого получены следующие данные:
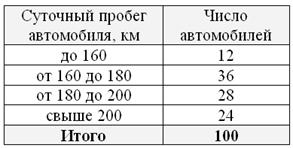
С вероятностью 0,954 требуется определить долю машин в генеральной совокупности с пробегом более 180 км.
Решение: вычислим количество автомобилей с пробегом более 180 км по выборке:
![]() . Таким образом:
. Таким образом:
![]() – выборочная доля автомобилей с пробегом более 180 километров.
– выборочная доля автомобилей с пробегом более 180 километров.
Генеральную долю ![]() таких автомобилей оценим с помощью доверительного интервала:
таких автомобилей оценим с помощью доверительного интервала:
![]() , где
, где ![]() – предельная ошибка доли.
– предельная ошибка доли.
Для уровня доверительной вероятности ![]() находим знакомый коэффициент доверия:
находим знакомый коэффициент доверия:
![]()
Следует отметить, что он не обязан быть целым, просто в задачах рассматриваемого типа почему-то любят предлагать нежные значения «гамма». Наверное, щадят студентов-экономистов, у которых эта задача – чуть ли не обязательная по предмету :) …а то таблицы Лапласа там всякие смотреть надо, жесть, короче :) А тут запомнил, и всё.
Вычислим среднюю ошибку доли. Коль скоро выборка 10%-ная, то объём генеральной совокупности равен ![]() автомобилей и для бесповторной выборки:
автомобилей и для бесповторной выборки:
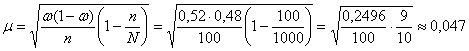
Таким образом, предельная ошибка доли ![]() и искомый доверительный интервал:
и искомый доверительный интервал:
![]()
![]() – с вероятностью 95,4% данный интервал накрывает истинную генеральную долю
– с вероятностью 95,4% данный интервал накрывает истинную генеральную долю ![]() автомобилей с пробегом более 180 км.
автомобилей с пробегом более 180 км.
Ответ: ![]()
Кстати, тут можно оценить и абсолютное количество таковых машин:
![]()
![]() – от 425 до 615 автомобилей.
– от 425 до 615 автомобилей.
Но результат, конечно, такой слабоватый. И помочь здесь может увеличение выборки.
Родственная формула уже выведена в предыдущем параграфе, и я просто заменю дисперсию произведением ![]() :
:
![]() – здесь по желаемой предельной ошибке можно вычислить необходимый объём выборки.
– здесь по желаемой предельной ошибке можно вычислить необходимый объём выборки.
И прямо сейчас у вас представится такая возможность. На десерт:
Пример 34
Методом механического отбора проведено однопроцентное обследование веса пирожных, изготовленных кондитерской фабрикой за сутки. Распределение веса пирожных по весу следующее:
![]()
а) С вероятностью 0,9973 определить пределы, в которых будет находиться доля пирожных весом не менее 100 г, во всей суточной продукции
б) Сколько процентов пирожных нужно проверить, чтобы улучшить оценку в 7 раз? (при той же доверительной вероятности)
Краткое решение и ответ в конце урока. И в его заключение пара слов о повторной выборке. На самом деле такую задачу мы уже разобрали на уроке об оценке вероятности биномиального распределения (Пример 29). Цитирую условие:
“
Проверив ![]() изделий, обнаружили, что
изделий, обнаружили, что ![]() изделий высшего сорта. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0,01?
изделий высшего сорта. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0,01?
”
Заметьте, что в этой задаче ничего не сказано о типе выборки, но, судя по всему, она бесповторна. Однако размер генеральной совокупности не указан, и поэтому ничего не остаётся, как предположить, что изделий очень много и использовать формулу ![]() повторной выборки.
повторной выборки.
С решением можно ознакомиться по ссылке выше (единственное, там буквы немного другие), ну а я ещё раз поздравляю всех с праздником – всем солнца, пирожных и автомобилей! И, конечно, хороших оценок ;)
Далее по курсу – Статистические гипотезы.
Решения и ответы:
Пример 31. Решение: вычислим исправленную выборочную дисперсию:
![]()
а) Вычислим предельную ошибку ![]() выборки.
выборки.
Так как ![]() , то коэффициент доверия найдём из соотношения
, то коэффициент доверия найдём из соотношения ![]() .
.
Примечание: ввиду небольшого объёма выборки хорошо смотрится и оценка по Стьюденту, что может быть даже предпочтительнее.
По условию, ![]() , следовательно:
, следовательно:
![]()
По таблице значений функции Лапласа находим, что этому значению функции соотвествует аргумент ![]()
Поскольку выборка 10%-ная бесповторная, то объём генеральной совокупности равен:
![]()
Вычислим среднюю ошибку выборки:
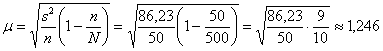
Таким образом, предельная ошибка:
![]() и искомый доверительный интервал:
и искомый доверительный интервал:
![]()
![]() – пределы, которые с доверительной вероятностью 0,954 накрывают среднее значение генеральной совокупности.
– пределы, которые с доверительной вероятностью 0,954 накрывают среднее значение генеральной совокупности.
б) Улучшим точность оценки в три раза: ![]() и воспользуемся формулой:
и воспользуемся формулой:
![]() (округлять лучше до бОльшего значения)
(округлять лучше до бОльшего значения)
Таким образом, для того, чтобы с вероятностью 95,4% утверждать, что ![]() отличается от
отличается от ![]() менее чем на
менее чем на ![]() , следует провести выборку объёмом примерно
, следует провести выборку объёмом примерно ![]() (что составляет половину генеральной совокупности, и, конечно, нецелесообразно).
(что составляет половину генеральной совокупности, и, конечно, нецелесообразно).
Ответ: а) ![]() , б)
, б) ![]()
Пример 34. Решение:
а) Вычислим количество пирожных весом не менее 100 грамм:
![]() . Таким образом:
. Таким образом:
![]() – выборочная доля таковых пирожных.
– выборочная доля таковых пирожных.
Соответствующую генеральную долю оценим с помощью доверительного интервала:
![]() , где
, где ![]() – предельная ошибка.
– предельная ошибка.
Уровню доверительной вероятности ![]() соответствует коэффициент
соответствует коэффициент ![]()
Вычислим среднюю ошибку доли. Поскольку выборка 1%-ная и бесповторная, то:
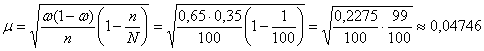
Таким образом, предельная ошибка доли ![]() и искомый доверительный интервал:
и искомый доверительный интервал:
![]()
![]() – данный интервал практически достоверно накрывает долю пирожных весом не менее 100 грамм во всей суточной партии.
– данный интервал практически достоверно накрывает долю пирожных весом не менее 100 грамм во всей суточной партии.
б) Улучшим точность оценки в 7 раз: ![]() и вычислим объём выборки, которую следует организовать, чтобы обеспечить эту точность. Учитывая, что объём генеральной совокупности составляет
и вычислим объём выборки, которую следует организовать, чтобы обеспечить эту точность. Учитывая, что объём генеральной совокупности составляет ![]() :
:
![]()
Таким образом, для того, чтобы с вероятностью 99,73% можно было утверждать, что выборочная доля ![]() пирожных весом не менее 100 грамм будет отличаться от истинного значения
пирожных весом не менее 100 грамм будет отличаться от истинного значения ![]() менее чем на 0,02, следует организовать выборку объёмом
менее чем на 0,02, следует организовать выборку объёмом ![]() пирожных, что составляет примерно треть генеральной совокупности.
пирожных, что составляет примерно треть генеральной совокупности.
Ответ: а) ![]() , б)
, б) ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
