
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
11. Статистические гипотезы
Надо сказать, капитально я «подзавяз» в интегралах, диффурах и тервере, и после основательной доработки этих разделов безмерно рад напечатать первый абзац 11-й статьи по матстату.
Есть ли жизнь после сессии смерти? Далеко не каждая гипотеза является статистической, и перед тем как перейти к теме, я на всякий случай поставлю ссылку на 1-й урок по математической статистике, если «чайникам» будет что-то не понятно в терминах.
Сначала кратко разберём теорию, затем наиболее распространённые задачи (сразу ссылка для «самоваров»). Зажигаем:
Пусть исследуется некоторый признак статистической совокупности. Успеваемость студентов, продолжительность жизни… каждый подумал о своём, точность измерений, да что угодно – хоть качество помидоров. Всё, что можно «оцифровать» и посчитать.
Как проводится исследование? Обычно так: из генеральной совокупности извлекается репрезентативная выборка (всё понятно?), и на основании изучения этой выборки делается вывод обо всей совокупности. Напоминаю, что это основной метод математической статистики и называется он выборочным методом. В зависимости от исследования, могут проводиться неоднократные выборки, выборки из нескольких ген. совокупностей, да и вообще анализироваться произвольные статистические данные.
И в результате анализа этих данных появляются мысли, которые оформляются в статистические гипотезы.
Статистической называют гипотезу о законе распределения статистической совокупности либо о числовых параметрах известных (!) распределений.
Например:
– рост танкистов распределен нормально;
– дисперсии стрельбы двух танковых дивизий равны между собой, при этом известно*, что точность стрельбы распределена нормально.
* из многочисленных ранее проведённых исследований.
В первом случае выдвигается гипотеза о законе распределения, во втором – о числовых характеристиках двух распределений, закон которых известен.
Откуда взялись эти гипотезы? В первом случае была проведена выборка танкистов (например, 100 человек) и в результате её исследования появилось обоснованное предположение, что рост ВСЕХ танкистов распределён нормально. Во втором случае исследовались выборочные данные по точности стрельбы двух дивизий, в результате чего возник интерес проверить – а одинакова ли генеральная результативность, или же какая-то дивизия стреляет точнее?
В обеих гипотезах речь идёт о генеральных совокупностях, и выдвигаются эти гипотезы на основании анализа выборочных данных. Это распространенная схема, но она не единственна, бывают и другие статистические гипотезы.
Выдвигаемую гипотезу называют нулевой и обозначают через ![]() . Обычно это наиболее очевидная и правдоподобная гипотеза (хотя это вовсе не обязательно). И в противовес к ней рассматривают альтернативную или конкурирующую гипотезу
. Обычно это наиболее очевидная и правдоподобная гипотеза (хотя это вовсе не обязательно). И в противовес к ней рассматривают альтернативную или конкурирующую гипотезу ![]() .
.
В рассмотренных выше примерах альтернативные гипотезы очевидны (отрицают нулевую), но существуют и другие варианты, так, например, к гипотезе ![]() : генеральная средняя нормально распределённой совокупности равна
: генеральная средняя нормально распределённой совокупности равна ![]() , можно сформулировать разные конкурирующие гипотезы:
, можно сформулировать разные конкурирующие гипотезы: ![]() или конкретно
или конкретно ![]() , это зависит от условия и данных той или иной задачи.
, это зависит от условия и данных той или иной задачи.
Поскольку нулевая гипотеза выдвигается на основе анализа ВЫБОРОЧНЫХ данных, то она может оказаться как правильной, так и неправильной. Более того, мы не сможем на 100% гарантировать её истинность либо ложность даже после статистической проверки! Ибо любая, самая «надёжная» выборка все равно остаётся выборкой и может нас дезинформировать (пусть с очень малой вероятностью).
Проверка осуществляется с помощью статистических критериев – это специальные случайные величины, которые принимают различные действительные значения. В разных задачах критерии разные, и мы рассмотрим их в конкретных примерах.
В результате проверки нулевая гипотеза либо принимается, либо отвергается в пользу альтернативной. При этом есть риск допустить ошибки двух типов:
Ошибка первого рода состоит в том, что гипотеза ![]() будет отвергнута, хотя на самом деле она правильная. Вероятность допустить такую ошибку называют уровнем значимости и обозначают буквой
будет отвергнута, хотя на самом деле она правильная. Вероятность допустить такую ошибку называют уровнем значимости и обозначают буквой ![]() («альфа»).
(«альфа»).
Ошибка второго рода состоит в том, что гипотеза ![]() будет принята, но на самом деле она неправильная. Вероятность совершить эту ошибку обозначают буквой
будет принята, но на самом деле она неправильная. Вероятность совершить эту ошибку обозначают буквой ![]() («бета»). Значение
(«бета»). Значение ![]() называют мощностью критерия – это вероятность отвержения неправильной гипотезы.
называют мощностью критерия – это вероятность отвержения неправильной гипотезы.
Уровень значимости задаётся исследователем самостоятельно, наиболее часто выбирают значения ![]() . И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении вероятности
. И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении вероятности ![]() - отвергнуть правильную гипотезу растёт вероятность
- отвергнуть правильную гипотезу растёт вероятность ![]() - принять неверную гипотезу (при прочих равных условиях). Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей
- принять неверную гипотезу (при прочих равных условиях). Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей ![]() и
и ![]() , при этом учитывается тяжесть последствий, которые повлекут за собой та и другая ошибки.
, при этом учитывается тяжесть последствий, которые повлекут за собой та и другая ошибки.
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я как раз приведу нестатистический пример…, опять напрашивается хардкор про диагностику болезни, но мы будем-таки настраиваться на позитив:
Танкист Вася поиграл с котами и зарегистрировался в почтовике. По умолчанию, ![]() – он считается добропорядочным пользователем. Так считает антиспам фильтр. И вот Вася отправляет письмо. После чего фильтр может совершить ошибку двух типов: 1) ошибочно отклонить нулевую гипотезу (счесть нормальное письмо за спам и Васю за спаммера) или 2) ошибочно принять нулевую гипотезу (хотя Вася редиска).
– он считается добропорядочным пользователем. Так считает антиспам фильтр. И вот Вася отправляет письмо. После чего фильтр может совершить ошибку двух типов: 1) ошибочно отклонить нулевую гипотезу (счесть нормальное письмо за спам и Васю за спаммера) или 2) ошибочно принять нулевую гипотезу (хотя Вася редиска).
Какая ошибка более «тяжелая»? Васино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра целесообразно уменьшить уровень значимости ![]() , пожертвовав вероятностью
, пожертвовав вероятностью ![]() , в результате чего в основной ящик будут чаще попадать письма особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью :)
, в результате чего в основной ящик будут чаще попадать письма особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью :)
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность ![]() следует увеличить (в пользу уменьшения вероятности
следует увеличить (в пользу уменьшения вероятности ![]() ). Примеры придумайте самостоятельно, самые прикольные опубликую :) …и садистских побольше, садистских =)
). Примеры придумайте самостоятельно, самые прикольные опубликую :) …и садистских побольше, садистских =)
Ну а теперь возвращаемся к статистике.
Процесс проверки статистической гипотезы состоит из следующих этапов:
1) Обработка выборочных данных и выдвижение основной ![]() и конкурирующей
и конкурирующей ![]() гипотез. К нулю, кстати, нулевая гипотеза не имеет никакого отношения, это просто историческое название, оно могло оказаться каким угодно.
гипотез. К нулю, кстати, нулевая гипотеза не имеет никакого отношения, это просто историческое название, оно могло оказаться каким угодно.
2) Выбор статистического критерия ![]() . Это непрерывная случайная величина, принимающая различные действительные значения. В разных задачах критерии разные.
. Это непрерывная случайная величина, принимающая различные действительные значения. В разных задачах критерии разные.
3) Выбор уровня значимости ![]() , о дилемме выбора этого значения я чуть-чуть рассказал выше.
, о дилемме выбора этого значения я чуть-чуть рассказал выше.
4) Нахождение критического значения ![]() – это значение случайной величины
– это значение случайной величины ![]() , которое зависит от выбранного уровня значимости
, которое зависит от выбранного уровня значимости ![]() и опционально от других параметров. Критическое значение определяет критическую область. Она бывает левосторонней, правосторонней и двусторонней (красная штриховка):
и опционально от других параметров. Критическое значение определяет критическую область. Она бывает левосторонней, правосторонней и двусторонней (красная штриховка):
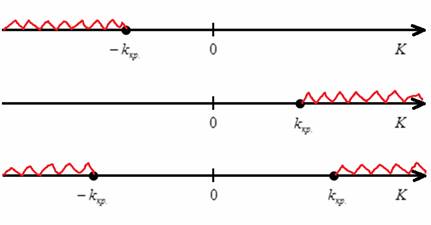
Критическая область – это область отвержения нулевой гипотезы. Незаштрихованную область называют областью принятия гипотезы.
Следует отметить, что это только одна из графических моделей. Существуют статистические критерии, которые принимают далеко не все действительные значения.
5) Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия: ![]() . И вердикт:
. И вердикт:
– Если ![]() в критическую область НЕ попадает, то гипотеза
в критическую область НЕ попадает, то гипотеза ![]() на уровне значимости
на уровне значимости ![]() принимается. Однако не нужно думать, что нулевая гипотеза доказана и является истиной, ведь существует вероятность
принимается. Однако не нужно думать, что нулевая гипотеза доказана и является истиной, ведь существует вероятность ![]() – того, что мы совершили ошибку 2-го рода (приняли неверную гипотезу).
– того, что мы совершили ошибку 2-го рода (приняли неверную гипотезу).
– Если ![]() попадает в критическую область, то гипотеза
попадает в критическую область, то гипотеза ![]() на уровне значимости
на уровне значимости ![]() отвергается (при этом, если, например,
отвергается (при этом, если, например, ![]() , то в среднем в 5 случаях из 100 мы отвергнем правильную гипотезу, т.е. совершим ошибку 1-го рода).
, то в среднем в 5 случаях из 100 мы отвергнем правильную гипотезу, т.е. совершим ошибку 1-го рода).
…Ну а что делать? – такая вот статистика неточная наука :)
И по горячей информации сразу разберём одну из наиболее распространённых гипотез:
Гипотеза о генеральной средней нормального распределения
Постановка задачи такова: предполагается, что генеральная средняя ![]() нормального распределения равна некоторому значению
нормального распределения равна некоторому значению ![]() . Это нулевая гипотеза:
. Это нулевая гипотеза:
![]()
Для проверки гипотезы на уровне значимости ![]() проводится выборка объема
проводится выборка объема ![]() и рассчитывается выборочная средняя
и рассчитывается выборочная средняя ![]() . Исходя из полученного значения и специфики той или иной задачи, можно сформулировать следующие конкурирующие гипотезы:
. Исходя из полученного значения и специфики той или иной задачи, можно сформулировать следующие конкурирующие гипотезы:
1) ![]()
2) ![]()
3) ![]()
4) ![]() , где
, где ![]() – конкретное альтернативное значение генеральной средней.
– конкретное альтернативное значение генеральной средней.
При этом возможны две принципиально разные ситуации:
а) если генеральная дисперсия 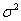 известна.
известна.
Тогда в качестве статистического критерия ![]() рассматривают случайную величину
рассматривают случайную величину ![]() , где
, где ![]() – случайное значение выборочной средней. Почему случайное? Потому что в разных выборках мы будем получать разные значения
– случайное значение выборочной средней. Почему случайное? Потому что в разных выборках мы будем получать разные значения ![]() , и заранее предугадать это значение невозможно.
, и заранее предугадать это значение невозможно.
Далее находим критическую область. Для конкурирующих гипотез ![]() и
и ![]() (случай
(случай ![]() ) строится левосторонняя область, для гипотез
) строится левосторонняя область, для гипотез ![]() и
и ![]() (случай
(случай ![]() ) – правосторонняя, и для гипотезы
) – правосторонняя, и для гипотезы ![]() – двусторонняя – т. к. конкурирующее значение генеральной средней может оказаться как больше, так и меньше
– двусторонняя – т. к. конкурирующее значение генеральной средней может оказаться как больше, так и меньше ![]() -го.
-го.
Чтобы найти критическую область нужно отыскать критическое значение ![]() . Оно определяется из соотношения
. Оно определяется из соотношения ![]() – для односторонней области (лево- или право-) и
– для односторонней области (лево- или право-) и ![]() – для двусторонней области, где
– для двусторонней области, где ![]() – выбранный уровень значимости, а
– выбранный уровень значимости, а ![]() – старая знакомая функция Лапласа.
– старая знакомая функция Лапласа.
Теперь на основании выборочных данных рассчитываем наблюдаемое значение критерия:
![]()
это можно было сделать и раньше, но такой порядок более последователен и логичен.
Результаты:
1) Для левосторонней критической области. Если ![]() , то гипотеза
, то гипотеза ![]() на уровне значимости
на уровне значимости ![]() принимается. Если
принимается. Если ![]() , то отвергается. И картинки тут недавно были, просто заменю букву:
, то отвергается. И картинки тут недавно были, просто заменю букву:
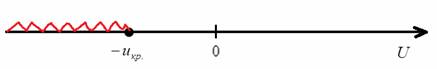
2) Правосторонняя критическая область. Если ![]() , то гипотеза
, то гипотеза ![]() принимается, в случае
принимается, в случае ![]() (красный цвет) – отвергается:
(красный цвет) – отвергается:
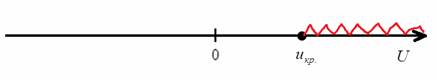
3) Двусторонняя критическая область. Если ![]() (незаштрихованный интервал), то гипотеза
(незаштрихованный интервал), то гипотеза ![]() принимается, в противном случае – отвергается:
принимается, в противном случае – отвергается:

условие принятия гипотезы часто записывают компактно – с помощью модуля:
![]()
И немедленно приступаем к задачам, а то по студенческим меркам я тут уже на пол диссертации наговорил:)
Пример 35
Из нормальной генеральной совокупности с известной дисперсией ![]() извлечена выборка объёма
извлечена выборка объёма ![]() и по ней найдена выборочная средняя
и по ней найдена выборочная средняя ![]() . Требуется на уровне значимости 0,01 проверить нулевую гипотезу
. Требуется на уровне значимости 0,01 проверить нулевую гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() .
.
Прежде чем приступить к решению, пару слов о смысле такой задачи. Есть генеральная совокупность с известной дисперсией и есть веские основания полагать, что генеральная средняя равна 20 (нулевая гипотеза). В результате выборочной проверки получена выборочная средняя 19,3, и возникает вопрос: это результат случайный или же генеральная средняя и на самом деле меньше двадцати? – в частности, равна 19 (конкурирующая гипотеза).
Решение: по условию, известна генеральная дисперсия ![]() , поэтому для проверки гипотезы
, поэтому для проверки гипотезы ![]() используем случайную величину
используем случайную величину ![]() .
.
Найдём критическую область. Для этого нужно найти критическое значение. Так как конкурирующее значение ![]() меньше чем
меньше чем ![]() , то критическая область будет левосторонней. Критическое значение определим из соотношения:
, то критическая область будет левосторонней. Критическое значение определим из соотношения:
![]() .
.
для уровня значимости ![]() :
:
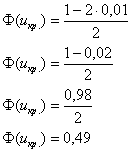
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что этому значению функции соответствует аргумент ![]() . Таким образом, при
. Таким образом, при ![]() (красная критическая область) нулевая гипотеза отвергается, а при
(красная критическая область) нулевая гипотеза отвергается, а при ![]() – принимается:
– принимается:
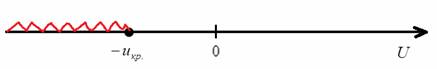
В данном случае ![]() .
.
Вычислим наблюдаемое значение критерия:
![]()
![]() , поэтому на уровне значимости
, поэтому на уровне значимости ![]() нулевую гипотезу
нулевую гипотезу ![]() принимаем.
принимаем.
Такой, вроде бы неожиданный результат, объясняется тем, что генеральное стандартное отклонение достаточно великО: ![]() , а посему нет оснований отвергать «главное» значение
, а посему нет оснований отвергать «главное» значение ![]() (несмотря на то, что выборочная средняя
(несмотря на то, что выборочная средняя ![]() гораздо ближе к конкурирующему значению
гораздо ближе к конкурирующему значению ![]() ). Иными словами, такое значение выборочной средней, вероятнее всего, объясняется естественным разбросом вариант
). Иными словами, такое значение выборочной средней, вероятнее всего, объясняется естественным разбросом вариант ![]() .
.
Ответ: на уровне значимости 0,01 нулевую гипотезу принимаем.
Что означает «на уровне значимости 0,01»? Это означает, что мы с 1%-ной вероятностью рисковали отвергнуть нулевую гипотезу, при условии, что она действительно справедлива. Однако не нужно забывать, что на самом деле она может быть и неверной и существует ![]() -вероятность того, мы приняли неправильную гипотезу. Примеры расчёта мощности критерия
-вероятность того, мы приняли неправильную гипотезу. Примеры расчёта мощности критерия ![]() для заданного уровня значимости
для заданного уровня значимости ![]() и различных конкурирующих значений можно найти, например, в учебном пособии задачнике В. Е. Гмурмана (поздние издания). Думал я, думал, и решил-таки этот материал в статью не включать, ибо задачка редкая, а материал не короткий.
и различных конкурирующих значений можно найти, например, в учебном пособии задачнике В. Е. Гмурмана (поздние издания). Думал я, думал, и решил-таки этот материал в статью не включать, ибо задачка редкая, а материал не короткий.
То была «обезличенная» задача, коих очень много, но мы будем менять мир к лучшему… физическими и химическими способами:) Заодно и понятнее будет, что здесь к чему:
Пример 36
По результатам ![]() измерений температуры в печи найдено
измерений температуры в печи найдено ![]() . Предполагается, что ошибка измерения есть нормальная случайная величина с
. Предполагается, что ошибка измерения есть нормальная случайная величина с ![]() . Проверить на уровне значимости
. Проверить на уровне значимости ![]() гипотезу
гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() .
.
Сначала разберём, в чём жизненность этой ситуации. Есть печка. Для нормального технологического процесса нужна температура 250 градусов. Для проверки этой нормы 5 раз измерили температуру, получили 256 градусов. Из многократных предыдущих опытов известно, что среднеквадратическая погрешность измерений составляет 6 градусов (она обусловлена погрешностью самого термометра, случайными обстоятельствами проверки и т.д.)
И здесь не понятно, почему выборочный результат (256 градусов) получился больше нормы – то ли температура действительно выше и печь нуждается в регулировке, то ли это просто погрешность измерений, которую можно не принимать во внимание.
Решение: по условию, известно ген. среднее квадратическое отклонение ![]() , поэтому для проверки гипотезы
, поэтому для проверки гипотезы ![]() используем случайную величину
используем случайную величину ![]() .
.
Найдём критическую область. Так как в конкурирующей гипотезе ![]() речь идёт о бОльших значениях температуры, то эта область будет правосторонней. Критическое значение определим из соотношения
речь идёт о бОльших значениях температуры, то эта область будет правосторонней. Критическое значение определим из соотношения ![]() . Для уровня значимости
. Для уровня значимости ![]() :
:
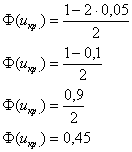
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что ![]() . Таким образом, при
. Таким образом, при ![]() (критическая область) нулевая гипотеза отвергается, а при
(критическая область) нулевая гипотеза отвергается, а при ![]() – принимается:
– принимается:
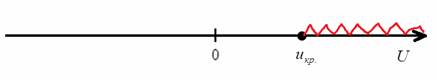
Вычислим наблюдаемое значение критерия:
![]()
![]() , поэтому на уровне значимости
, поэтому на уровне значимости ![]() нулевую гипотезу
нулевую гипотезу ![]() отвергаем.
отвергаем.
Как бы сказали статистики, выборочный результат ![]() статистически значимо отличается от нормативного значения
статистически значимо отличается от нормативного значения ![]() , и печь нуждается в регулировке (для уменьшения температуры).
, и печь нуждается в регулировке (для уменьшения температуры).
Ответ: на уровне значимости ![]() гипотезу
гипотезу ![]() отвергаем.
отвергаем.
Ещё раз осмыслим – что означает «на уровне значимости 0,05»? Это означает, что с вероятностью 5% мы отвергли правильную гипотезу (совершили ошибку 1-го рода). И тут остаётся взвесить риск – насколько критично чуть-чуть уменьшить температуру (если мы всё-таки ошиблись и температура на самом деле в норме). Если даже небольшое уменьшение температуры недопустимо, то имеет смысл провести повторное, более качественное исследование: увеличить количество замеров ![]() , использовать более совершенный термометр, улучшить условия эксперимента и т.д.
, использовать более совершенный термометр, улучшить условия эксперимента и т.д.
Следующая задача для самостоятельного решения, и на всякий случай я ещё раз продублирую ссылку на таблицу значений функции Лапласа и Калькулятор:
Пример 37
Средний вес таблетки сильнодействующего лекарства (номинал) должен быть равен 0,5 мг. Выборочная проверка ![]() выпущенных таблеток показала, что средний вес таблетки равен
выпущенных таблеток показала, что средний вес таблетки равен ![]() мг. Многократными предварительными опытами по взвешиванию таблеток, изготавливаемых фармацевтическим заводом, установлено, что вес таблеток распределен нормально со средним квадратическим отклонением
мг. Многократными предварительными опытами по взвешиванию таблеток, изготавливаемых фармацевтическим заводом, установлено, что вес таблеток распределен нормально со средним квадратическим отклонением ![]() мг. Требуется на уровне значимости
мг. Требуется на уровне значимости ![]() проверить гипотезу о том, что средний вес таблеток действительно равен
проверить гипотезу о том, что средний вес таблеток действительно равен ![]() .
.
Рассмотрите как конкурирующую гипотезу ![]() , так и гипотезу
, так и гипотезу ![]() . И в самом деле – ведь полученное значение
. И в самом деле – ведь полученное значение ![]() является случайным и в другой выборке оно может запросто оказаться и меньше чем 0,5.
является случайным и в другой выборке оно может запросто оказаться и меньше чем 0,5.
Краткое решение и ответы, как обычно, в конце урока.
Кстати, это тот самый пример, где ошибка 2-го рода (ошибочное принятие неверной нулевой гипотезы), может повлечь гораздо более тяжелые последствия (опасную передозировку). Поэтому в такой ситуации лучше включить паранойю и увеличить уровень значимости до ![]() – при этом мы будем чаще отвергать правильную нулевую гипотезу (совершать ошибку 1-го рода), но зато перестрахуемся и проведём более тщательное исследование.
– при этом мы будем чаще отвергать правильную нулевую гипотезу (совершать ошибку 1-го рода), но зато перестрахуемся и проведём более тщательное исследование.
Можно ли одновременно уменьшить вероятности ошибок 1-го и 2-го рода (![]() и
и ![]() )? Да можно. Если увеличить объём выборки. Что вполне логично.
)? Да можно. Если увеличить объём выборки. Что вполне логично.
Теперь вторая ситуация. Та же самая задача, почти всё то же самое, но:
б) генеральная дисперсия 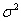 НЕ известна.
НЕ известна.
В этом случае остаётся ориентироваться на исправленную выборочную дисперсию ![]() и критерий
и критерий ![]() , где
, где ![]() – случайное значение выборочной средней и
– случайное значение выборочной средней и ![]() – соответствующее исправленное стандартное отклонение. Данная случайная величина имеет распределение Стьюдента с
– соответствующее исправленное стандартное отклонение. Данная случайная величина имеет распределение Стьюдента с ![]() степенями свободы.
степенями свободы.
Алгоритм решения полностью сохраняется:
Пример 38
На основании ![]() измерений найдено, что средняя высота сальниковой камеры равна
измерений найдено, что средняя высота сальниковой камеры равна ![]() мм и
мм и ![]() мм. В предположении о нормальном распределении проверить на уровне значимости
мм. В предположении о нормальном распределении проверить на уровне значимости ![]() гипотезу
гипотезу ![]() мм против конкурирующей гипотезы
мм против конкурирующей гипотезы ![]() мм.
мм.
И начнём мы опять со смысла задачи, что здесь произошло? Здесь 7 раз измерили высоту этой камеры, получили среднее значение 51 мм и за неимением генеральной дисперсии вычислили исправленную выборочную дисперсию. Но, согласно норме, высота должна равняться 50 мм – эту гипотезу и проверяем.
Решение: так как генеральная дисперсия не известна, то для проверки гипотезы ![]() используем случайную величину
используем случайную величину ![]() .
.
Конкурирующая гипотеза имеет вид ![]() , а значит, речь идёт о двусторонней критической области. Критическое значение можно найти по таблице распределения Стьюдента либо с помощью Калькулятора (Пункт 10в). Для уровня значимости
, а значит, речь идёт о двусторонней критической области. Критическое значение можно найти по таблице распределения Стьюдента либо с помощью Калькулятора (Пункт 10в). Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() :
:
![]()
Таким образом, при ![]() нулевая гипотеза принимается, и вне этого интервала (в критической области при
нулевая гипотеза принимается, и вне этого интервала (в критической области при ![]() ) – отвергается:
) – отвергается:
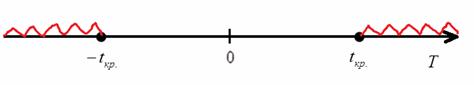
Вычислим наблюдаемое значение критерия:
![]() – полученное значение попало в область принятия гипотезы (
– полученное значение попало в область принятия гипотезы (![]() ), поэтому на уровне значимости 0,05 нулевую гипотезу принимаем.
), поэтому на уровне значимости 0,05 нулевую гипотезу принимаем.
Ответ: на уровне значимости 0,05 гипотезу ![]() мм принимаем.
мм принимаем.
То есть, с точки зрения статистики, выборочный результат ![]() мм, скорее всего (! но это не точно), обусловлен погрешностью выборки, и на самом деле высота сальниковой камеры соответствует норме (50 мм).
мм, скорее всего (! но это не точно), обусловлен погрешностью выборки, и на самом деле высота сальниковой камеры соответствует норме (50 мм).
Творческая задача для самостоятельного решения:
Пример 39
Нормативный расход автомобильного двигателя составляет 10 л на 100 км. После конструктивных изменений, направленных на уменьшение этого показателя, были получены следующие результаты 10 тестовых заездов:
![]()
На уровне значимости 0,05 выяснить, действительно ли расход топлива стал меньше.
Да, это не редкость – когда в предложенной задаче нужно не только проверить гипотезу, но и предварительно рассчитать выборочные значения. Кстати, даже при известной генеральной дисперсии, ориентироваться на неё тут нельзя, ибо конструктивные изменения могут изменить не только генеральную среднюю, но и генеральную дисперсию.
В лучших традициях курса все числа уже забиты в Эксель – там же инструкция по расчётам выборочных показателей. Если кто-то не знает или запамятовал, то вот ролик о том, как провести эти вычисления быстро (Ютуб).
В данной задаче критическая область левосторонняя, и критическое значение ![]() для односторонней области отыскивается по самой нижней строке таблицы или с помощью Калькулятора (тот же Пункт 10в).
для односторонней области отыскивается по самой нижней строке таблицы или с помощью Калькулятора (тот же Пункт 10в).
Постарайтесь грамотно оформить решение, свериться с образцом можно чуть ниже.
И я жду вас на следующем уроке, где мы продолжим проверять статистические гипотезы.
Решения и ответы:
Пример 37. Решение: поскольку известно ген. стандартное отклонение, то для проверки гипотезы ![]() используем случайную величину
используем случайную величину ![]() .
.
а) Рассмотрим конкурирующую гипотезу ![]() . Так как альтернативные значения генеральной средней больше чем 0,5, то находим правостороннюю критическую область. Критическое значение определим из соотношения
. Так как альтернативные значения генеральной средней больше чем 0,5, то находим правостороннюю критическую область. Критическое значение определим из соотношения ![]() . Для уровня значимости
. Для уровня значимости ![]() :
:
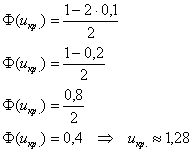
При ![]() гипотеза принимается, при
гипотеза принимается, при ![]() (критическая область) – отвергается.
(критическая область) – отвергается.
Вычислим наблюдаемое значение критерия:
![]()
![]() , таким образом, на уровне значимости 0,1 гипотезу
, таким образом, на уровне значимости 0,1 гипотезу ![]() принимаем.
принимаем.
б) Рассмотрим конкурирующую гипотезу ![]() . В данном случае критическая область двусторонняя. Критическое значение найдём из соотношения
. В данном случае критическая область двусторонняя. Критическое значение найдём из соотношения ![]() .
.
Для ![]() :
:
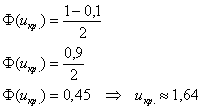
При ![]() гипотеза принимается, а при
гипотеза принимается, а при ![]() (красная критическая область) – отвергается:
(красная критическая область) – отвергается:

Наблюдаемое значение критерия ![]() вычислено в предыдущем пункте, и оно попадает в область принятия гипотезы.
вычислено в предыдущем пункте, и оно попадает в область принятия гипотезы.
Ответ: в обоих случаях нулевую гипотезу на уровне значимости 0,1 принимаем.
Пример 39. Решение: вычислим сумму вариант ![]() , выборочную среднюю
, выборочную среднюю ![]() , квадраты отклонений
, квадраты отклонений ![]() и их сумму
и их сумму ![]() .
.
Вычисления удобно свести в таблицу:
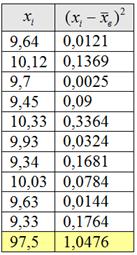
Выборочная дисперсия:
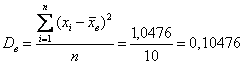
Исправленная выборочная дисперсия:
![]()
Исправленное стандартное отклонение.
![]()
На уровне значимости 0,05 проверим нулевую гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() . Для проверки используем случайную величину
. Для проверки используем случайную величину ![]() .
.
Найдём критическую область. Поскольку в конкурирующей гипотезе речь идёт о меньших значениях, то она будет левосторонней. Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() по таблице критических точек распределения Стьюдента, найдём критическое значение для односторонней области:
по таблице критических точек распределения Стьюдента, найдём критическое значение для односторонней области:
![]()
Таким образом, при ![]() нулевая гипотеза отвергается, а при
нулевая гипотеза отвергается, а при ![]() – принимается:
– принимается:
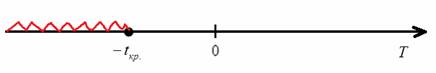
Вычислим наблюдаемое значение критерия:
![]()
![]() , поэтому на уровне значимости 0,05 нулевую гипотезу
, поэтому на уровне значимости 0,05 нулевую гипотезу ![]() отвергаем, иными словами, выборочное значение
отвергаем, иными словами, выборочное значение ![]() статистически значимо отличается от 10.
статистически значимо отличается от 10.
Ответ: на уровне значимости 0,05 можно утверждать, что расход топлива стал ниже.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
