
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Экстремумы функций двух и трёх переменных
Поздравляю всех читателей сайта с большим событием – после кропотливой и технически сложной разработки темы функций нескольких переменных, наконец-то появилась на свет эта долгожданная статья! Сегодня на уроке мы научимся находить максимумы и минимумы функций двух и трёх переменных, а также обобщим алгоритм решения данной задачи на случай бОльшего количества аргументов. С понятиями точек экстремума и экстремумов вы уже знакомы из статьи об экстремумах функции одной переменной, и для «старших сестёр» эти понятия имеют родственный смысл. Освежим в памяти элементарную терминологию:
– точки экстремума – это общее название точек минимума и максимума;
– экстремумы – это общее название минимумов и максимумов.
Начнём с функции двух переменных ![]() , применительно к которой точки экстремума – это точки плоскости
, применительно к которой точки экстремума – это точки плоскости ![]() , а экстремумы – соответствующие значения функции («высоты»). Также экстремумами иногда называют точки самой поверхности.
, а экстремумы – соответствующие значения функции («высоты»). Также экстремумами иногда называют точки самой поверхности.
Да, и сразу важное напутствие для «чайников», нормальных студентов =) и сомневающихся – рассматриваемый материал сам по себе прост, но требует базовых знаний и навыков в нескольких разделах высшей математики. Поэтому если у вас возникнет (или уже возникло) какое-либо недопонимание по ходу изложения, то проставленные ссылки в помощь.
Итак, «действующие лица» следующие: функция ![]() , внутренняя точка
, внутренняя точка ![]() её области определения и
её области определения и ![]() -окрестность данной точки. Для удобства считаем, что окрестность представляет собой круг радиуса
-окрестность данной точки. Для удобства считаем, что окрестность представляет собой круг радиуса ![]() с центром в точке
с центром в точке ![]() (в учебной литературе чаще встречается окрестность-квадрат).
(в учебной литературе чаще встречается окрестность-квадрат).
Определение: если в некоторой ![]() -окрестности точки
-окрестности точки ![]() выполнено неравенство
выполнено неравенство ![]() , то говорят, что функция
, то говорят, что функция ![]() имеет минимум в точке
имеет минимум в точке ![]() .
.
При этом точка ![]() называется точкой минимума, а соответствующее значение функции
называется точкой минимума, а соответствующее значение функции ![]() («высота») – минимумом. Ещё раз призываю не путаться в терминах!
(«высота») – минимумом. Ещё раз призываю не путаться в терминах!
Простейший пример минимума – это вершина эллиптического параболоида, чаша которого направлена вверх:
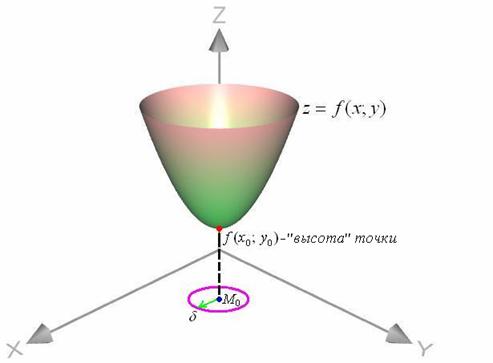
Давайте ещё раз внимательно перечитаем определение и вдумаемся в его суть. Сформулированное определение говорит нам о том, что функция ![]() достигает минимума в точке
достигает минимума в точке ![]() , если существует хоть какая-то
, если существует хоть какая-то ![]() -окрестность этой точки, в которой значение высоты
-окрестность этой точки, в которой значение высоты ![]() меньше ВСЕХ ОСТАЛЬНЫХ значений
меньше ВСЕХ ОСТАЛЬНЫХ значений ![]() .
.
Следует отметить, что в нашем примере под определение подходит вообще любая ![]() -окрестность, т.к. поверхность уходит вверх на бесконечность и никаких точек ниже – нет в принципе. Такой минимум называют глобальным.
-окрестность, т.к. поверхность уходит вверх на бесконечность и никаких точек ниже – нет в принципе. Такой минимум называют глобальным.
А теперь мысленно разверните чашу параболоида вниз – чтобы красная точка стала «вершиной горы».
Определение: если в некоторой ![]() -окрестности точки
-окрестности точки ![]() выполнено неравенство
выполнено неравенство ![]() , то говорят, что функция
, то говорят, что функция ![]() имеет максимум в точке
имеет максимум в точке ![]() .
.
Соответственно, точка ![]() называется точкой максимума, а значение
называется точкой максимума, а значение ![]() – максимумом функции.
– максимумом функции.
В случае с нашим параболоидом максимум, естественно, тоже глобальный, но на практике гораздо чаще встречаются локальные экстремумы. Так, например, функция ![]() на нижеследующем чертеже достигает локального максимума (слева вверху) и локального минимума (справа внизу):
на нижеследующем чертеже достигает локального максимума (слева вверху) и локального минимума (справа внизу):
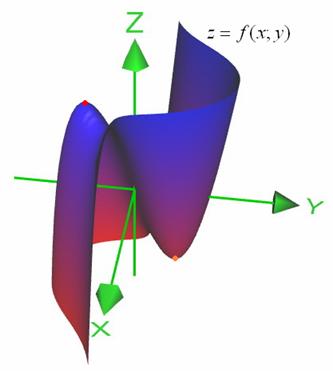
Наверное, всем понятно, в чём различие, но всё-таки закомментирую: почему, например, такой максимум называют локальным? Потому что функция на своей области определения достигает и бОльших значений – по правую руку поверхность уходит «за облака», где о красной точке разве что легенды слагают. Таким образом, о «вершине горы» речь идёт лишь на локальном участке области определения. «Гора», кстати, «горЕ» рознь – бывают поверхности, у которых минимумы и максимумы если и различимы на глаз, то выглядят, как пупырышки =) Важно, чтобы существовала пусть даже очень малая ![]() -окрестность точки
-окрестность точки ![]() , где выполнено условие минимума или максимума (см. определения).
, где выполнено условие минимума или максимума (см. определения).
Из вышесказанного следует ещё одна важная вещь, которая опять же касается понятий. Пожалуйста, РАЗЛИЧАЙТЕ и будьте аккуратны в выражениях:
максимум функции – это в общем случае НЕ ТО ЖЕ САМОЕ, что максимальное значение функции;
минимум функции – это в общем случае НЕ ТО ЖЕ САМОЕ, что минимальное значение функции.
Да, в примере с эллиптическим параболоидом соответствующие понятия совпадают, но вот у только что рассмотренной поверхности «красный» максимум – это отнюдь не наибольшее, а «оранжевый» минимум – отнюдь не наименьшее значение функции. Задачу нахождения минимального и максимального значений функции мы рассмотрим в самом ближайшем будущем, а пока что вернёмся к теме сегодняшнего урока:
Как исследовать функцию 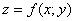 на экстремум?
на экстремум?
Прежде всего, нужно ориентироваться на необходимое условие экстремума:
если дифференцируемая функция ![]() имеет экстремум в точке
имеет экстремум в точке ![]() , то обе частные производные 1-го порядка в данной точке равны нулю:
, то обе частные производные 1-го порядка в данной точке равны нулю:
![]()
Точку, удовлетворяющую этим условиям, называют критической, а чаще – стационарной точкой.
! Примечание: условие необходимо именно для дифференцируемой в точке ![]() функции. Как мы увидим в Примере 6, экстремум может существовать и при других обстоятельствах.
функции. Как мы увидим в Примере 6, экстремум может существовать и при других обстоятельствах.
Обратное утверждение справедливо далеко не всегда. Иными словами, если известно, что в некоторой точке ![]() частные производные равны нулю, то это ЕЩЁ НЕ ЗНАЧИТ, что там есть экстремум. Его там может и не быть.
частные производные равны нулю, то это ЕЩЁ НЕ ЗНАЧИТ, что там есть экстремум. Его там может и не быть.
Так, например, у функции ![]() , которая как раз задаёт эллиптический параболоид, частные производные
, которая как раз задаёт эллиптический параболоид, частные производные ![]() обращаются в ноль в точке
обращаются в ноль в точке ![]() – и в данной точке действительно существует минимум функции («дно чаши»).
– и в данной точке действительно существует минимум функции («дно чаши»).
Но у функции ![]() с производными
с производными ![]() , равными нулю в этой же точке, не наблюдается ничего подобного. Это гиперболический параболоид или «седло»:
, равными нулю в этой же точке, не наблюдается ничего подобного. Это гиперболический параболоид или «седло»:
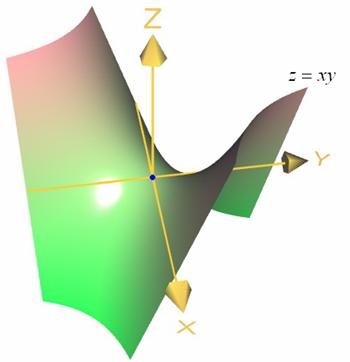
Для точки ![]() не существует
не существует ![]() -окрестности, в которой поверхность располагалась бы только вверху
-окрестности, в которой поверхность располагалась бы только вверху ![]() или только внизу
или только внизу ![]() . Грубо говоря, в любой
. Грубо говоря, в любой ![]() -окрестности точки
-окрестности точки ![]() куски поверхности есть и сверху, и снизу.
куски поверхности есть и сверху, и снизу.
Точку такого рода так и называют – седловой, а иногда, по известной географической ассоциации – точкой перевала.
Читатели, знакомые с материалами статьи Производная по направлению и градиент, наверное, уже поняли геометрический смысл выкладок: из условий
![]() следует равенство нулю производной и по всем направлениям:
следует равенство нулю производной и по всем направлениям: ![]() . То есть, если мы сделаем бесконечно малый «шажок» из точки
. То есть, если мы сделаем бесконечно малый «шажок» из точки ![]() в любую сторону, то наша высота останется неизменной. И этот факт справедлив, как для точек экстремума, так и для точки перевала.
в любую сторону, то наша высота останется неизменной. И этот факт справедлив, как для точек экстремума, так и для точки перевала.
Итак, условия ![]() необходимы для существования экстремума дифференцируемой там функции, но на основании только этой информации мы ещё не можем сделать вывода о характере точки
необходимы для существования экстремума дифференцируемой там функции, но на основании только этой информации мы ещё не можем сделать вывода о характере точки ![]() . С достаточным условием экстремума познакомимся прямо по ходу практической задачи, а то что-то мы засиделись в теории:
. С достаточным условием экстремума познакомимся прямо по ходу практической задачи, а то что-то мы засиделись в теории:
Пример 1
Исследовать на экстремум функцию
![]()
Решение: на первом шаге нужно отыскать стационарные точки. Для этого найдём частные производные 1-го порядка:
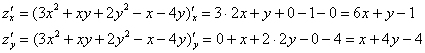
Контроль: ![]()
и решим систему:
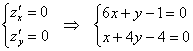
В данном случае получена система двух линейных уравнений с двумя неизвестными, которую можно решить несколькими способами. Но мудрить здесь не надо – как проще, так и решаем. Из 2-го уравнения выразим ![]() и подставим в 1-е уравнение:
и подставим в 1-е уравнение:
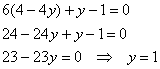
Таким образом: ![]()
![]() – стационарная точка. Тут, главное, не перепутать координаты.
– стационарная точка. Тут, главное, не перепутать координаты.
Выполним промежуточную проверку:
![]()
Отлично. А точнее, хорошо, поскольку пройдено всего лишь пол пути. В найденной точке может быть минимум, максимум либо перевал, и выяснить, что же там на самом деле, нам поможет
достаточное условие экстремума функции двух переменных,
для применения которого нужно вычислить частные производные 2-го порядка в точке ![]() Для компактности обычно используют следующие обозначения:
Для компактности обычно используют следующие обозначения:
![]()
Если ![]() , то функция
, то функция ![]() имеет экстремум в точке
имеет экстремум в точке ![]() , причём, если
, причём, если ![]() , то это минимум, а если
, то это минимум, а если ![]() – то максимум.
– то максимум.
Примечание: здесь также можно ориентироваться и на букву «цэ», т.к. неравенство ![]() выполняется только в том случае, если
выполняется только в том случае, если ![]() и
и ![]() – одного знака.
– одного знака.
Если ![]() , то в точке
, то в точке ![]() нет экстремума.
нет экстремума.
Если же ![]() , то требуется дополнительное исследование, о котором загадочно умалчивают практически все источники. Впрочем, беспокоиться особо не нужно – встретите вряд ли.
, то требуется дополнительное исследование, о котором загадочно умалчивают практически все источники. Впрочем, беспокоиться особо не нужно – встретите вряд ли.
В нашем примере все частные производные 2-го порядка равны константам:
![]()
а значит, соответствующим константам они равны и в частности в точке ![]() :
:
![]()
Таким образом: ![]() , следовательно, в точке
, следовательно, в точке ![]() есть экстремум, и так как
есть экстремум, и так как ![]() , то это – минимум. Осталось его найти. Перепишем функцию
, то это – минимум. Осталось его найти. Перепишем функцию ![]() , чтобы она была перед глазами, и ОЧЕНЬ внимательно проведём вычисления:
, чтобы она была перед глазами, и ОЧЕНЬ внимательно проведём вычисления:
![]()
Надо сказать, момент весьма неприятный, поскольку здесь существует ненулевая вероятность запороть всё задание. Правда, в данном случае вычисления здОрово облегчил нулевой «икс».
Ответ: ![]()
Признаюсь честно, привык я рисовать значки ![]() , что не есть хорошо, т.к. они обычно используются для обозначения минимального и максимального значений функции. От чего вас и предостерегаю.
, что не есть хорошо, т.к. они обычно используются для обозначения минимального и максимального значений функции. От чего вас и предостерегаю.
И справка для любознательных: поверхность ![]() представляет собой не что иное, как «подзашифорованный» эллиптический параболоид – весьма похожий на тот, который мы видели на 1-й картинке урока.
представляет собой не что иное, как «подзашифорованный» эллиптический параболоид – весьма похожий на тот, который мы видели на 1-й картинке урока.
Пара разминочных примеров для самостоятельного решения:
Пример 2
Исследовать на экстремум функцию двух переменных
![]()
Пример 3
Исследовать на экстремум функцию двух переменных
![]()
Решение 3-го примера осложняется тем, что получается система нелинейных уравнений. Подумайте, что и откуда выгоднее выразить. Примерный образец чистового оформления задач в конце урока.
Когда я подбирал материалы к этой статье, то обнаружил у себя целую тьму подобных примеров (даже сам удивился) и поэтому рекомендую со всей ответственностью отнестись к предлагаемым заданиям.
Нередко приходится разбираться с двумя или даже бОльшим количествам стационарных точек. Типовая задача с экспонентой:
Пример 4
Исследовать функцию на экстремум
![]()
Решение: чтобы определить стационарные точки, найдем частные производные 1-го порядка и приравняем их к нулю. Техническая сложность дифференцирования состоит в применении правила ![]() , после чего, руководствуясь здравой логикой, нужно «загонять» слагаемые в одну скобку и по необходимости «наводить там порядок»:
, после чего, руководствуясь здравой логикой, нужно «загонять» слагаемые в одну скобку и по необходимости «наводить там порядок»:
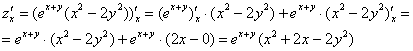
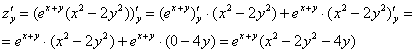
На всякий пожарный проверим, что ![]() (тем более, находить всё равно придётся):
(тем более, находить всё равно придётся):
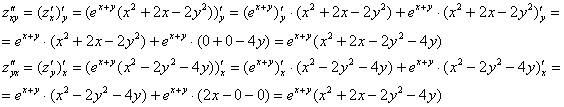
ОК
Составляем систему:
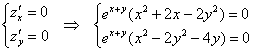
Поскольку экспоненты не могут равняться нулю, то их можно с чистой совестью убрать:
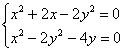
В подобных системах нужно проявить смекалку: где-то удаётся удачно выразить одну переменную через другую, где-то можно выделить полный квадрат, ну а у нас решение лежит на поверхности:
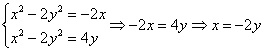
(к такому же результату приводит вычитание одного уравнения из другого)
Теперь подставляем соотношение ![]() в любое, например, во 2-е уравнение системы:
в любое, например, во 2-е уравнение системы:
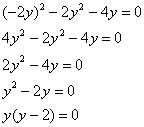
В результате получены 2 стационарные точки:
![]()
Не упущу возможности позанудствовать и напомнить о проверке – координаты найденных точек должны удовлетворять каждому уравнению системы.
Достаточное условие экстремума, как вы понимаете, нужно проверить для каждой точки отдельно. И в том, и в другом случае нам потребуются частные производные 2-го порядка:
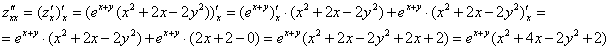
Смешанная производная уже найдена:
![]()
И, наконец, «двойная игрековая»:
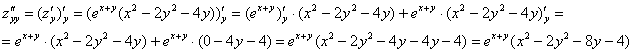
...Это ещё не самый страх – пример я подобрал довольно гуманный =)
На очереди кропотливые вычисления:
1) Проверим выполнение достаточного условия экстремума для точки ![]() :
:
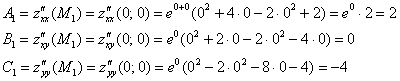
![]() , значит, в точке
, значит, в точке ![]() нет экстремума.
нет экстремума.
2) Проверим выполнение достаточного условия экстремума для точки ![]() :
:
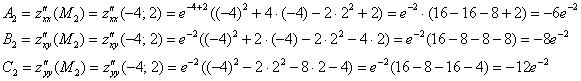
![]() , значит, в точке
, значит, в точке ![]() существует экстремум, и поскольку
существует экстремум, и поскольку ![]() , то это – максимум. Вспоминаем про функцию
, то это – максимум. Вспоминаем про функцию ![]() и НЕ ОШИБАЕМСЯ:
и НЕ ОШИБАЕМСЯ:
![]()
Ответ: ![]()
О точке перевала ![]() в ответе не упоминаем. Зачем? Нас же просили провести исследование на экстремум.
в ответе не упоминаем. Зачем? Нас же просили провести исследование на экстремум.
От следующего задания тоже трудно отказаться – почти баян:
Пример 5
Исследовать функцию на экстремум
![]()
Краткое решение и ответ в конце урока
Время от времени посетители сайта просят меня включать в уроки задания и посложнее… ну что же, нашёлся тут интересный экземпляр: ![]() . Здесь придётся разрулить не самую простую систему и проверить на экстремум несколько стационарных точек. Чтобы не убивать интригу, в конце урока не будет ни решения, ни ответа =)
. Здесь придётся разрулить не самую простую систему и проверить на экстремум несколько стационарных точек. Чтобы не убивать интригу, в конце урока не будет ни решения, ни ответа =)
И специально для всех читателей mathprofi.ru, можно сказать, эксклюзивная задача:
Пример 6
Исследовать функцию на экстремум
![]()
Решение начинается как обычно:
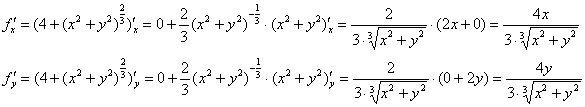
Но вот следующий шаг, казалось бы, сразу приводит к ответу об отсутствии экстремумов:
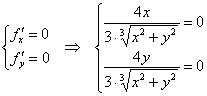
Система не имеет решений, поскольку единственная «подозрительная» точка ![]() обращает знаменатели в ноль, то есть функция
обращает знаменатели в ноль, то есть функция ![]() – не дифференцируема в данной точке. Но неужели всё так просто? И действительно – ведь САМА-ТО функция там определена:
– не дифференцируема в данной точке. Но неужели всё так просто? И действительно – ведь САМА-ТО функция там определена:
![]()
И более того, поверхность ![]() непрерывна в точке
непрерывна в точке ![]() (да и вообще в любой точке плоскости
(да и вообще в любой точке плоскости ![]() ). Так почему же тут не может существовать минимум или максимум?
). Так почему же тут не может существовать минимум или максимум?
Сомнения не напрасны! По аналогии с похожим «плоским» случаем (см. Пример 8 урока Возрастание, убывание и экстремумы функции) такая точка тоже считается стационарной и в ней тоже может быть экстремум!
Но здесь возникает второй камень преткновения. В знаменателях частных производных 2-го порядка (проверьте самостоятельно) находятся корни ![]() , что делает невозможным вычисление значений
, что делает невозможным вычисление значений ![]() .
.
Как быть? В трудной ситуации всегда есть смысл проанализировать самое простое решение. А самое элементарное в экстремумах – это непосредственно их определения!
Рассмотрим достаточно малую ![]() -окрестность точки
-окрестность точки ![]() . Любую точку данной окрестности, отличную от
. Любую точку данной окрестности, отличную от ![]() , можно представить в виде
, можно представить в виде ![]() , где значения
, где значения ![]() не равны нулю одновременно и достаточно малы для того чтобы точка
не равны нулю одновременно и достаточно малы для того чтобы точка ![]() входила в эту окрестность.
входила в эту окрестность.
Примечание: оба числа могут быть положительны ![]() , отрицательны
, отрицательны ![]() , разных знаков:
, разных знаков: ![]() либо
либо ![]() ; и, кроме того, одно из них может равняться нулю (ещё 4 случая). Таким образом, обозначение
; и, кроме того, одно из них может равняться нулю (ещё 4 случая). Таким образом, обозначение ![]() действительно пригодно.
действительно пригодно.
Вычислим значение функции в этой произвольной точке окрестности:
![]()
Так как ![]() не равны нулю одновременно, то корень
не равны нулю одновременно, то корень ![]() будет хоть чуть-чуть, но больше нуля, а значит,
будет хоть чуть-чуть, но больше нуля, а значит, ![]() . И вспоминая, что
. И вспоминая, что ![]() , записываем очевидный факт:
, записываем очевидный факт: ![]() . Грубо говоря, в рассматриваемой окрестности значение
. Грубо говоря, в рассматриваемой окрестности значение ![]() «самое низкое».
«самое низкое».
Вывод: для точки ![]() нашлась
нашлась ![]() -окрестность, в которой выполнено неравенство
-окрестность, в которой выполнено неравенство ![]() , таким образом,
, таким образом, ![]() – минимум по определению.
– минимум по определению.
Нетрудно понять, что минимум глобальный. Геометрически поверхность представляет собой своеобразное пространственное остриё, а точнее – «шип».
Ответ: ![]()
Представленное решение полностью корректно и полноценно! Более того, данный способ можно попытаться применить и в ситуации, когда достаточное условие экстремума не даёт ответа ![]() . Однако дело осложняется тем, что неравенство
. Однако дело осложняется тем, что неравенство ![]() либо
либо ![]() нужно обосновать для каждого из восьми случаев (см. Примечание), что реально осуществимо далеко не всегда. Зависит от функции.
нужно обосновать для каждого из восьми случаев (см. Примечание), что реально осуществимо далеко не всегда. Зависит от функции.
И заключительный, не менее интересный параграф:
Экстремумы функции трёх переменных
Плюс одно измерение. Рассмотрим функцию трёх переменных ![]() , внутреннюю точку
, внутреннюю точку ![]() её области определения и
её области определения и ![]() -окрестность данной точки, которая представляет собой шар с центром в точке
-окрестность данной точки, которая представляет собой шар с центром в точке ![]() радиуса
радиуса ![]() .
.
Определение: если в некоторой ![]() -окрестности точки
-окрестности точки ![]() выполнено неравенство
выполнено неравенство ![]() (
(![]() – точка
– точка ![]() -шара, отличная от
-шара, отличная от ![]() ), то функция
), то функция ![]() имеет минимум в точке
имеет минимум в точке ![]() ; если же
; если же ![]() – то максимум.
– то максимум.
Вполне, кстати, понятное и не такое уж абстрактное определение.
Всё очень похоже. Если дифференцируемая функция ![]() имеет экстремум в точке
имеет экстремум в точке ![]() , то обязательно выполняются условия
, то обязательно выполняются условия ![]() . Но с другой стороны, если в какой-либо точке производные 1-го порядка равны нулю, то это ещё не значит, что там есть экстремум.
. Но с другой стороны, если в какой-либо точке производные 1-го порядка равны нулю, то это ещё не значит, что там есть экстремум.
Алгоритм решения сохраняется прежним:
Пример 7
Найти экстремумы функции
![]()
Решение: переключаем передачу на частные производные функции трёх переменных:
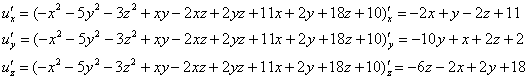
Чтобы найти стационарные точки, составим и решим следующую систему:
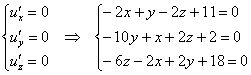
Аккуратно расположим переменные в обычном порядке и, кроме того, разделим последнее уравнение на 2:
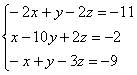
Систему можно решить методом Гаусса, но зачем такие сложности? Из 3-го уравнения выразим ![]() и подставим его в первые два уравнения:
и подставим его в первые два уравнения:
![]()
Из 1-го уравнения выразим ![]() и подставим во 2-е уравнение:
и подставим во 2-е уравнение:
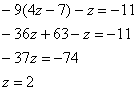
Таким образом:
![]()
Таким образом, ![]() – стационарная точка. Здесь, напоминаю, не помешает подставить найденное решение
– стационарная точка. Здесь, напоминаю, не помешает подставить найденное решение ![]() в каждое уравнение исходной системы и убедиться в выполнении условий
в каждое уравнение исходной системы и убедиться в выполнении условий ![]() .
.
Проверка достаточного условия экстремума осуществляется несколько по-другому. Сначала нужно найти все частные производные 2-го порядка, вычислить их в точке ![]() и составить так называемую матрицу Гессе:
и составить так называемую матрицу Гессе:
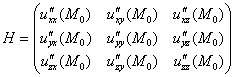
Да не пугайтесь вы так =) Данная матрица является симметричной (или симметрической). Это значит, что её элементы симметричны относительно главной диагонали, на которой в данном случае расположены «однобуквенные» частные производные ![]() . Уловили закономерность?
. Уловили закономерность?
Далее нужно вычислить угловые миноры. Это определители, которые «разрастаются» из левого верхнего угла:
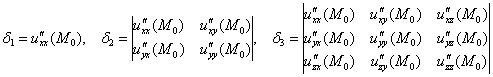
1) Если ![]() , то функция
, то функция ![]() достигает минимума в точке
достигает минимума в точке ![]() .
.
2) Если ![]() (так и только так!), то функция
(так и только так!), то функция ![]() достигает максимума в точке
достигает максимума в точке ![]() .
.
3) Если получилось что-то другое и при этом ![]() , то
, то ![]() – седловая точка. Здесь это уже во многом условное название.
– седловая точка. Здесь это уже во многом условное название.
4) Если ![]() , то признак не даёт ответа о характере точки
, то признак не даёт ответа о характере точки ![]() .
.
Внимательные читатели заметили, что эту схему в варианте «два на два» мы использовали и в предыдущем параграфе – только оформление «детское» было. Но не будем отвлекаться.
В нашем примере все производные 2-го порядка равны константам:
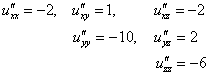
а значит, они равны константам и в точке ![]() . Составим матрицу Гессе:
. Составим матрицу Гессе:
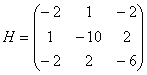
и вычислим её угловые миноры:
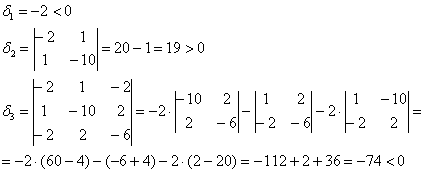
Вывод: функция достигает максимума в точке ![]() .
.
Для удобства вычислений скопирую функцию:
![]()
![]()
Ответ: ![]()
Аналогичное задание для закрепления материала:
Пример 8
Исследовать функцию на экстремум
![]()
Краткое решение и ответ рядом.
Рассмотренный алгоритм исследования распространяется и на функции бОльшего количества переменных. Я бы мог расписать его в общем виде, но заметная часть аудитории просто на дух не переносит общие формулы с нагромождением цифр и индексов. Поэтому разберём ещё случай функции 4 переменных, а дальше – будет понятно.
Чтобы исследовать на экстремум дифференцируемую функцию ![]() четырёх аргументов, нужно найти частные производные 1-го порядка и решить систему:
четырёх аргументов, нужно найти частные производные 1-го порядка и решить систему:
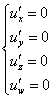
Предположим, что в результате решения найдена стационарная точка ![]() . Далее нужно найти частные производные 2-го порядка, вычислить их в точке
. Далее нужно найти частные производные 2-го порядка, вычислить их в точке ![]() и составить матрицу Гессе:
и составить матрицу Гессе:
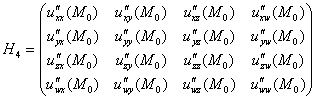
после чего вычислить её угловые миноры ![]() .
.
Если все миноры положительны, то в точке ![]() – минимум, если знакочередуются в следующем порядке:
– минимум, если знакочередуются в следующем порядке: ![]() (и именно в таком!), то в точке
(и именно в таком!), то в точке ![]() – максимум. Если имеет место другой случай, но
– максимум. Если имеет место другой случай, но ![]() , то
, то ![]() – седловая точка; если же
– седловая точка; если же ![]() , то признак не даёт ответа о характере точки
, то признак не даёт ответа о характере точки ![]() .
.
Ну и для совсем продвинутых читателей сообщу, что это есть не что иное, как проверка квадратичной формы полного дифференциала 2-го порядка на знакоопределённость методом Сильвестра (для функций 2, 3, 4 и бОльшего количества переменных).
Удачных вам исследований!
На следующих уроках мы познакомимся с условными экстремумами, задачей нахождения минимального и максимального значений функции, а также известнейшим приложением темы – Методом наименьших квадратов.
Как наберётесь сил – приходите ещё! =)
Решения и ответы:
Пример 2: Решение: найдём стационарные точки:
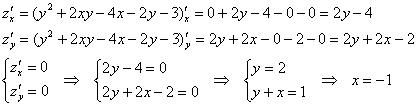
![]() – стационарная точка.
– стационарная точка.
Проверим выполнение достаточного условия экстремума:
![]() , в частности:
, в частности:
![]()
![]() , значит, в точке
, значит, в точке ![]() нет экстремума.
нет экстремума.
Ответ: экстремумы отсутствуют
Пример 3: Решение: найдём стационарные точки:
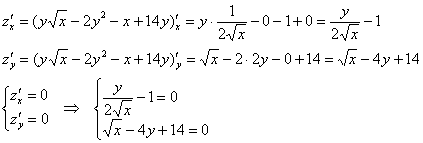
Из 1-го уравнения выразим: ![]() – подставим во 2-е уравнение:
– подставим во 2-е уравнение:
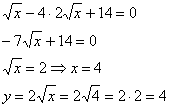
![]() – стационарная точка.
– стационарная точка.
Проверим выполнение достаточного условия экстремума:
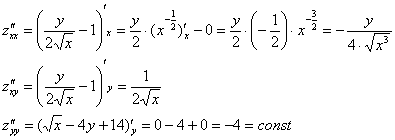
Таким образом:
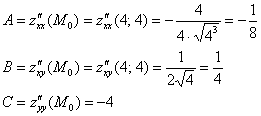
![]() , значит, в точке
, значит, в точке ![]() существует экстремум, так как
существует экстремум, так как ![]() , то это – максимум:
, то это – максимум:
![]()
Ответ: ![]()
Пример 5: Решение: найдем частные производные 1-го порядка:
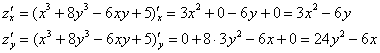
Составим и решим систему:
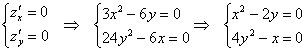
Из 2-го уравнения выразим ![]() – подставим в 1-е уравнение:
– подставим в 1-е уравнение:
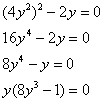
В результате получены 2 стационарные точки:
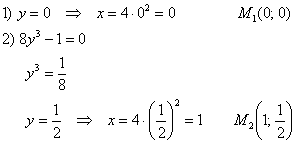
Проверим выполнение достаточного условия экстремума:
![]()
1) Для точки ![]() :
:
![]()
![]() , значит, в точке
, значит, в точке ![]() нет экстремума.
нет экстремума.
2) Для точки ![]() :
:
![]()
![]() , значит, в точке
, значит, в точке ![]() существует экстремум, и поскольку
существует экстремум, и поскольку ![]() , то это минимум:
, то это минимум:
![]()
Ответ: ![]()
Пример 8: Решение: найдём стационарные точки:
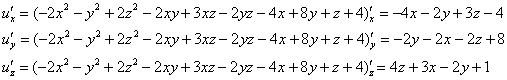
Составим и решим систему:
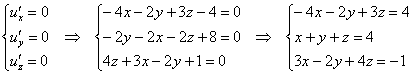
Из 2-го уравнения выразим ![]() – подставим в 1-е и 3-е уравнения:
– подставим в 1-е и 3-е уравнения:
![]()
Из 2-го уравнения выразим ![]() – подставим в 1-е уравнение:
– подставим в 1-е уравнение:
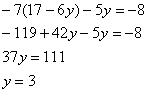
Таким образом:
![]()
![]() – стационарная точка.
– стационарная точка.
Найдём частные производные 2-го порядка:
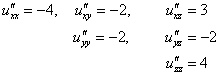
Частные производные равны константами, а значит, они равны соответствующим константам и в точке ![]() . Составим матрицу Гессе:
. Составим матрицу Гессе:
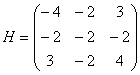
и вычислим её угловые миноры:
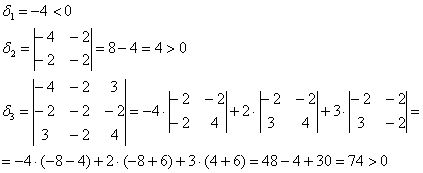
Ответ: экстремумы отсутствуют
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
