Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Метод Эйлера. Усовершенствованный метод Эйлера.
Классический метод Рунге-Кутты

Не обошла стороной вычислительная математика и дифференциальные уравнения! Сегодня на уроке мы познакомимся с основами приближённых вычислений в этом разделе математического анализа, после чего перед вами приветливо распахнутся толстые-претолстые книги по теме. Ибо вычислительная математика стороной диффуры ещё как не обошла =)

Перечисленные в заголовке методы предназначены для приближённого нахождения решений дифференциальных уравнений, систем ДУ, и краткая постановка наиболее распространённой задачи такова:

Рассмотрим дифференциальное уравнение первого порядка , для которого требуется найти частное решение, соответствующее начальному условию . Что это значит? Это значит, нам нужно найти функцию  (предполагается её существование), которая удовлетворяет данному дифф. уравнению, и график которой проходит через точку .

Но вот незадача – переменные в уравнении  разделить невозможно. Никакими известными науке способами. А если и возможно, то получается неберущийся интеграл. Однако частное-то решение существует! И здесь на помощь приходят методы приближенных вычислений, которые позволяют с высокой (а зачастую с высочайшей) точностью «сымитировать» функцию   на некотором промежутке.

Идея методов Эйлера и Рунге-Кутты состоит в том, чтобы заменить фрагмент графика  ломаной линией, и сейчас мы узнаем, как эта идея реализуется на практике. И не только узнаем, но и непосредственно реализуем =) Начнём с исторически первого и самого простого метода. …Вы хотите иметь дело со сложным дифференциальным уравнением? Вот и я тоже не хочу:)

Задание

Найти частное решение дифференциального уравнения , соответствующее начальному условию , методом Эйлера на отрезке  с шагом . Построить таблицу и график приближённого решения.

Разбираемся. Во-первых, перед нами обычное линейное уравнение, которое можно решить стандартными способами, и поэтому очень трудно устоять перед соблазном сразу же найти точное решение:

 – желающие могут выполнить проверку и убедиться, что данная функция удовлетворяет начальному условию  и является корнем уравнения .

Что нужно сделать? Нужно найти и построить ломаную, которая приближает график функции  на промежутке . Поскольку длина этого промежутка равна единице, а шаг составляет , то наша ломаная будет состоять из 10 отрезков:

причём, точка  уже известна – она соответствует начальному условию . Кроме того, очевидны «иксовые» координаты  других точек:

Осталось найти . Никакого дифференцирования и интегрирования – только сложение и умножение! Каждое следующее «игрековое» значение получается из предыдущего по простой рекуррентной формуле:

Представим дифференциальное уравнение  в виде :

Таким образом:

«Раскручиваемся» от начального условия :

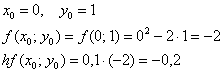
Понеслось:

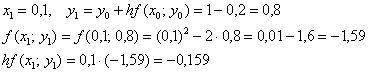
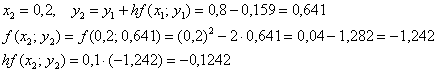
и так далее – до победного конца.

Результаты вычислений удобно заносить в таблицу:

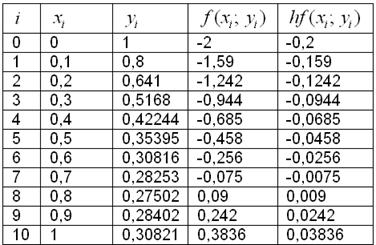
А сами вычисления автоматизировать в Экселе – потому что в математике важен не только победный, но ещё и быстрый конец:)

По результатам 2-го и 3-го столбцов изобразим на чертеже 11 точек  и 10 отрезков, соединяющих смежные точки.  Для сравнения я построю график точного частного решения :

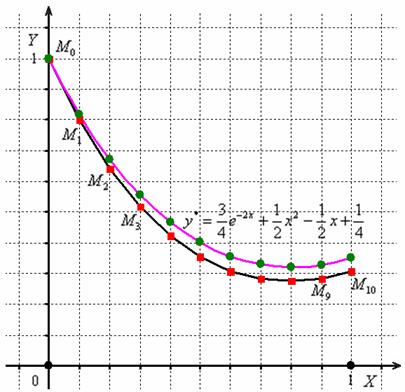
Существенным недостатком простого метода Эйлера является слишком большая погрешность, при этом легко заметить, что погрешность имеет тенденцию накапливаться – чем дальше мы уходим от точки , тем преимущественно больше становится расхождение между приближением и истиной. Это объяснимо самим принципом, который Эйлер положил в основу своего метода: отрезки  параллельны соответствующим касательным к графику функции  в точках . Данный факт, кстати, тоже хорошо просматривается по чертежу.

Как можно улучшить приближение? Первая мысль – измельчить разбиение. Разделим отрезок , например, на 20 частей. Тогда шаг составит: , и совершенно понятно, что ломаная из 20 звеньев заметно точнее приблизит частное решение. С помощью того же Экселя не составит труда обработать 100-1000 и даже миллион (!) промежуточных отрезков, однако зададимся вопросом: а нельзя ли КАЧЕСТВЕННО улучшить метод?

Но перед тем как раскрыть этот вопрос, не могу не остановиться на неоднократно прозвучавшей сегодня фамилии. Читая биографию Леонарда Эйлера, просто поражаешься, как невероятно много может успеть сделать за свою жизнь  человек! Сопоставимо вспомнился только К.Ф. Гаусс. …Вот и мы постараемся не потерять мотивацию к обучению и новым открытиям:))

Усовершенствованный метод Эйлера

Рассмотрим тот же самый пример: дифференциальное уравнение , частное решение, удовлетворяющее условию , промежуток  и его разбиение на 10 частей
( – длина каждой части).

Цель усовершенствования состоит в том, чтобы приблизить «красные квадратики» ломаной  к соответствующим «зелёным точкам» точного решения .

И идея модификации такова: отрезки  должны быть параллельны касательным, которые проведены к графику функции  не на левых краях, а «посерединке» интервалов разбиения. Что, естественно, улучшит качество приближения.

Алгоритм решения работает в том же русле, но формула, как нетрудно догадаться, усложняется:
, где

Плясать вновь начинаем от частного решения  и сразу же находим 1-й аргумент «внешней» функции:

Далее следуют уже знакомые по предыдущему параграфу вычисления , после чего можно рассчитать 2-й аргумент «внешней» функции: .

Теперь находим нашего «монстра», который на поверку оказался не таким уж и страшным – обратите внимание, что это ТА ЖЕ функция , вычисленная в другой точке:

Умножаем результат на шаг разбиения:

Таким образом:

Алгоритм заходит на второй круг, не поленюсь, распишу его подробно:

рассматриваем пару  и находим 1-й аргумент «внешней» функции:

Рассчитываем  и находим её 2-й аргумент:

Вычислим значение:

и его произведение на шаг:

Таким образом:

Далее рассматриваем пару  и т. д.

Вычисления разумно провести в Экселе (растиражировав формулы по той же схеме – см. видеоролик выше), а результаты свести в таблицу:

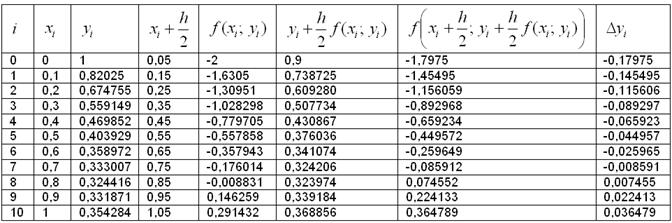
Числа целесообразно округлять до 4-5-6 знаков после запятой. Нередко в условии той или иной задачи есть прямое указание, с какой точностью следует проводить округление. Я подровнял сильно «хвостатые» значения до 6 знаков.

По результатам 2-го и 3-го столбцов (слева) построим ломаную , и для сравнения я снова приведу график точного решения :

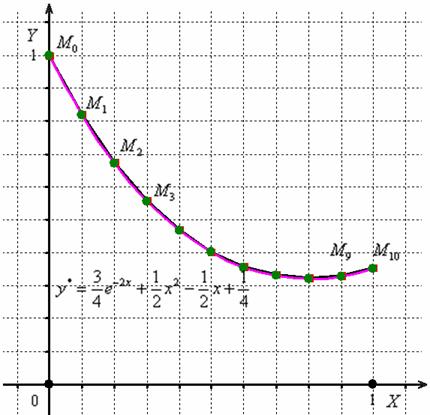
Результат существенно улучшился! – красные квадратики  практически «спрятались» за зелёными точками точного решения.

Однако нет пределов совершенству. Одна голова хорошо, а две – лучше. И снова немецкие:

Классический метод Рунге-Кутты 4-го порядка

Его цель добиться ещё бОльшего приближения «красных квадратиков» к «зелёным точкам». Вы спросите, куда ещё ближе? Во многих, в частности физических, исследованиях бывает ПРИНЦИПИАЛЬНО важен 10-й, а то и 50-й точный знак после запятой. Нет, такой точности можно достичь и простым методом Эйлера, но на СКОЛЬКО частей придётся разбить промежуток ?! …Хотя с современными вычислительными мощностями это не проблема – тысячи кочегаров китайского космического корабля гарантируют!

И, как правильно подсказывает заголовок, при использовании метода Рунге-Кутты на каждом шаге нам придётся вычислить значение функции  4 раза (в отличие от двукратного вычисления в предыдущем параграфе). Но задача эта вполне и вполне подъёмная если нанять китайцев. Каждое следующее «игрековое» значение получается из предыдущего  – ловим формулы:
, где , где:

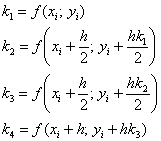
Готовы? Ну тогда начинаем:))

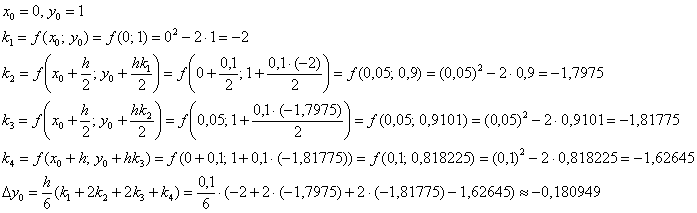
Таким образом:

Первая строка запрограммирована, и я копирую формулы по образцу:

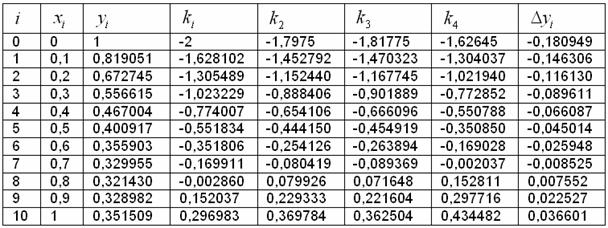
Не думал, что так быстро разделаюсь с методом Рунге-Кутты =)

В чертеже нет смысла, поскольку он уже не показателен. Давайте лучше проведём аналитическое сравнение точности трёх методов, ибо когда известно точное решение  , то грех не сравнить. Значения функции  в узловых точках элементарно рассчитываются в том же Экселе – один раз забиваем формулу  и тиражируем её на остальные .

В нижеследующую таблицу я сведу значения  (для каждого из трёх методов) и соответствующие абсолютные погрешности  приближённых вычислений:

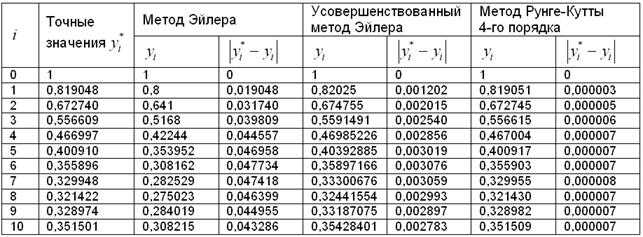
Как видите, метод Рунге-Кутты даёт уже 4-5 верных знака после запятой по сравнению с 2 верными знаками усовершенствованного метода Эйлера! И это не случайность:

– Погрешность «обычного» метода Эйлера не превосходит шага разбиения. И в самом деле – взгляните на самый левый столбец погрешностей  – там после запятых только один ноль, что и говорит нам о точности 0,1.

– Усовершенствованный метод Эйлера гарантирует точность:  (смотрим на 2 нуля после запятой в средней колонке погрешностей).

– И, наконец, классический метод Рунге-Кутты обеспечивает точность .

Изложенные оценки погрешностей строго обосновывается в теории.

Как можно ЕЩЁ улучшить точность приближения? Ответ прямо-таки философский: качеством и/или количеством =) В частности, существует и другие, более точные модификации метода Рунге-Кутты. Количественный путь, как уже отмечалось, состоит в уменьшении шага, т. е. в разбиении отрезка  на бОльшее количество  промежуточных отрезков. И с увеличением этого количества ломаная  всё больше и больше будет походить на график точного решения  и в пределе – совпадёт с ним.

В математике это свойство называется спрямляемостью кривой. К слову (небольшой оффтоп), «спрямить» удаётся далеко не всё – рекомендую прочитать интереснейшую статью о фракталах, в которых уменьшение «участка исследования» не влечёт за собой упрощение объекта исследования.

Так получилось, что я разобрал всего лишь одно дифференциальное уравнение и поэтому пара дополнительных замечаний. Что ещё нужно иметь в виду на практике? В условии задачи вам может быть предложен другой отрезок и другое разбиение, причём иногда встречается следующая формулировка: «найти методом… …на промежутке , разбив его на 5 частей». В этом случае нужно найти шаг разбиения , после чего придерживаться обычной схемы решения. Кстати, начальное условие должно быть такого вида: , то есть «икс нулевое», как правило, совпадает с левым концом отрезка. Образно говоря, ломаная всегда «выходит» из точки .

Безусловным достоинством рассмотренных методов, является тот факт, что они применимы к уравнениям  с очень сложной правой частью. И безусловный недостаток – далеко не каждый диффур можно представить в таком виде.

Но почти всё в этой жизни поправимо! – ведь мы рассмотрели лишь малую толику темы, и моя фраза о толстых-претолстых книгах была вовсе не шуткой. Существует великое множество приближённых методов нахождения решений ДУ и их систем, в которых применяются, в том числе, принципиально другие подходы. Так, например, частное решение можно приблизить степенным рядом. Однако это уже статья другого раздела.

Надеюсь, мне удалось разнообразить скучноватую вычислительную математику, и вам было интересно!

Спасибо за внимание!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте