
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Теория поля
Известная также, как векторный анализ. А кому-то векторный анализ, известный как теория поля =) Наконец-то мы добрались до этой интереснейшей темы! Данный раздел высшей математики язык не поворачивается назвать простым, однако ж, в грядущих статьях я постараюсь достигнуть двух целей:
а) чтобы все понимали, о чём вообще идёт разговор;
б) и чтобы «чайники» научились решать, как минимум, простые вещи – хотя бы на уровне заданий, которые предлагаются студентам-заочникам.
Весь материал будет изложен в популярном стиле, и если вам нужна более строгая и полная информация, то можно взять, например, 3-й том Фихтенгольца или заглянуть в Вики.
И сразу расшифруем заголовок. С теорией, думаю, всё понятно – в лучших традициях сайта мы разберём её основы и сделаем основной упор на практику. Ну а с чем у вас ассоциируется слово «поле»?
Поле с травой, футбольное поле…. Ещё? Поле деятельности, поле экспериментов. Приветствую гуманитариев! …Из школьного курса? Электрическое поле, магнитное, электромагнитное…, так, хорошо. Гравитационное поле Земли, в котором мы находимся. Отлично! Так, кто это там сказал о поле действительных и комплексных чисел? …совсем какие-то монстры здесь собрались! =) Благо, алгебра уже пройдена.
На ближайших уроках мы познакомимся со специфическим понятием поля, конкретными примерами из жизни, а также научимся решать тематические задачи векторного анализа. Теорию поля лучше всего изучать, как вы правильно догадываетесь, на поле – природе, где есть лес, речка, озеро, деревенский домик, и я приглашаю всех погрузиться если и не в тёплую летнюю реальность, то в приятные воспоминания:
ПолЯ в рассматриваемом сегодня смысле бывают скалярные и векторные, и начнём мы с их «кирпичиков».
Во-первых, скаляр. Довольно-таки часто этот термин ошибочно отождествляют с числом. Нет, всё обстоит немного не так: скаляр – это величина, каждое значение которой может быть выражено лишь одним числом. В физике примеров масса: длина, ширина, площадь, объём, плотность, температура и др. Всё это скалярные величины. И, кстати, масса – тоже пример.
Во-вторых, вектор. Алгебраического определения вектора я коснулся на уроке о линейных преобразованиях и одну из его частных ипостасей не знать просто невозможно =) Типичный вектор выражается двумя или бОльшим количеством чисел (своими координатами). И даже для одномерного вектора лишь одного числа не достаточно – по той причине, что у вектора есть ещё направление. И точка приложения, если вектор не свободен. Векторами характеризуют силовые физические поля, скорость и многие другие величины.
Ну что же, теперь можно приступить к сбору алюминиевых огурцов урожая:
Скалярное поле
Если каждой точке ![]() некоторой области пространства поставлено в соответствие определённое число
некоторой области пространства поставлено в соответствие определённое число ![]() (чаще действительное), то говорят, что в этой области задано скалярное поле.
(чаще действительное), то говорят, что в этой области задано скалярное поле.
Рассмотрим, например, исходящий из земли перпендикулярный луч. Воткните для наглядности лопату =) Какие скалярные поля можно задать на этом луче? Первое, что напрашивается – это поле высоты – когда каждой точке ![]() луча поставлена в соответствие её высота над уровнем земли. Или, например, поле атмосферного давления – здесь каждой точке луча соответствует числовое значение атмосферного давления в данной точке.
луча поставлена в соответствие её высота над уровнем земли. Или, например, поле атмосферного давления – здесь каждой точке луча соответствует числовое значение атмосферного давления в данной точке.
Теперь подойдём к озеру и мысленно проведём над его поверхностью плоскость. Если каждой точке ![]() «водного» фрагмента плоскости поставить в соответствие глубину озера, то, пожалуйста – скалярное поле задано. В этих же точках можно рассмотреть и другие скалярные величины, например, температуру поверхности воды.
«водного» фрагмента плоскости поставить в соответствие глубину озера, то, пожалуйста – скалярное поле задано. В этих же точках можно рассмотреть и другие скалярные величины, например, температуру поверхности воды.
Важнейшим свойством скалярного поля является его инвариантность относительно системы координат. Если перевести на человеческий язык, то с какой бы стороны мы на лопату / озеро ни посмотрели – скалярное поле (высота, глубина, температура и т.д.) от этого не изменятся. Более того, скалярное поле, скажем, глубины можно ведь задать и на другой поверхности, например, на подходящей полусфере, или непосредственно на самой водной поверхности. А почему нет? Разве нельзя каждой точке полусферы, расположенной над озером, поставить в соответствие число? Плоскость я предложил исключительно ради удобства.
Добавим ещё одну координату. Возьмите в руку камень. Каждой точке ![]() этого камня можно поставить в соответствие его физическую плотность. И опять – в какой бы системе координат мы его ни рассмотрели, как бы ни крутили в руке – скалярное поле плотности останется неизменным. Впрочем, некоторые люди могут оспорить этот факт =) Такой вот философский камень.
этого камня можно поставить в соответствие его физическую плотность. И опять – в какой бы системе координат мы его ни рассмотрели, как бы ни крутили в руке – скалярное поле плотности останется неизменным. Впрочем, некоторые люди могут оспорить этот факт =) Такой вот философский камень.
С чисто математической точки зрения (вне физического или другого частного смысла) скалярные поля традиционно задают нашими «обычным» функциями одной ![]() , двух
, двух ![]() , трёх
, трёх ![]() и бОльшего количества переменных. При этом в теории поля в широком ходу традиционные атрибуты этих функций, такие как, область определения, линии и поверхности уровня.
и бОльшего количества переменных. При этом в теории поля в широком ходу традиционные атрибуты этих функций, такие как, область определения, линии и поверхности уровня.
Так, линии уровня глубины озера представляют собой замкнутые непересекающиеся линии на плоскости. Каждая из этих линий соответствует определённому значению глубины, и по соответствующей «плоской» карте мы можем судить о рельефе дна – где мелководье, где «обрывы» и т.д.
Поверхности уровня представляют собой непересекающиеся пространственные поверхности, «вложенные» друг в друга. Или «лежащие» друг на друге. Или… у кого на что фантазии хватит =) Каждой такой поверхности соответствует постоянное значение скалярного поля, например, какая-то конкретная температура.
Однако наши «обычные» числа и функции задают скалярные поля далеко не всегда! Приведу классический пример с вектором – для определённости рассмотрим геометрический вектор плоскости ![]() в некоторой аффинной системе координат. Что произойдёт, если перейти к новому базису? В общем случае данный вектор поменяет координаты:
в некоторой аффинной системе координат. Что произойдёт, если перейти к новому базису? В общем случае данный вектор поменяет координаты: ![]() .
.
Координаты вектора – это числа? Числа. Но скалярными величинами они не являются! Поскольку скаляры не зависят от системы координат. Более того, координаты векторов можно ведь задать и «обычными» функциями – и эти функции не будут порождать скалярное поле!
Надо сказать, ловким получился переход к следующему параграфу:
Векторное поле
Если каждой точке ![]() некоторой области пространства поставлен в соответствие вектор с началом в данной точке, то говорят, что в этой области задано векторное поле.
некоторой области пространства поставлен в соответствие вектор с началом в данной точке, то говорят, что в этой области задано векторное поле.
Из чего следует, что элементы векторного поля не свободны, то есть «привязаны» к точкам. И почему векторы в «неволе» – становится ясно из простых примеров. В частности, на уроке о криволинейных интегралах по замкнутому контуру мы провели «плоский» опыт с магнитом на столе: чем ближе к магниту поднести железку, тем сильнее она притягивается. И эта сила в той или иной точке поверхности стола как раз характеризуется вектором напряжённости магнитного поля. Чем сильнее притяжение, тем длиннее вектор, ну и его остриё, понятно, указывает направление действия силы.
Но гораздо чаще векторные поля рассматривают в трёхмерном пространстве, пожалуйста: наша Земля – тот же больший магнит. Другой пример – её гравитационное поле. Чем дальше от поверхности, тем меньше сила тяжести и тем короче соответствующие силовые векторы. Кстати, куда они «смотрят»? Говоря просто, все они направлены к центру нашей планеты.
Большую группу векторных полей образуют так называемые поля скоростей. Посмотрите на поле (которое с травкой) и мысленно очертите над ним произвольную пространственную область. Представьте, что над полем дует ветер – небольшой такой ураганчик для пущей наглядности. Теперь зафиксируем некоторый момент времени и каждой точке построенной области поставим в соответствие несвободный вектор, который характеризует:
а) направление движения воздуха в данной точке;
б) и скорость его движения в данной точке – чем выше скорость, тем длиннее вектор. Если в какой-то точке штиль, то ей сопоставляется нулевой вектор.
Множество этих векторов и образует векторное поле скорости ветра в данный момент времени.
Аналогично устроено поле скоростей течения жидкости – так, например, каждой точке реки в некоторый момент времени можно поставить в соответствие вектор, указывающий направление и скорость течения жидкости в этой точке.
Да чего там ветер и река, поле скорости можно смоделировать собственноручно, для этого достаточно взмахнуть рукой. Или даже моргнуть глазом.
…Какой же кошмар! – векторы вокруг нас! В «ужастиках» эту роль играют зомби или живые мертвецы, а в реальности-то вот оно, оказывается как – ВЕКТОРЫ.
С формально-математической точки зрения, векторные поля задают векторными функциями, которые уже «проскакивали» в других темах:
Для «плоского» случая – это векторная функция ![]() , которая различным точкам
, которая различным точкам ![]() плоскости
плоскости ![]() * ставит в соответствие несвободные векторы
* ставит в соответствие несвободные векторы ![]() – конкретный пример есть в параграфе Работа векторного поля. Если функции двух переменных
– конкретный пример есть в параграфе Работа векторного поля. Если функции двух переменных ![]() определены при любых «икс», «игрек», то векторное поле будет задано на всей плоскости
определены при любых «икс», «игрек», то векторное поле будет задано на всей плоскости ![]() .
.
* Далее по умолчанию считаем, что все дела происходят в декартовой системе координат
С трёхмерным пространством всё аналогично:
![]() – здесь каждой допустимой точке
– здесь каждой допустимой точке ![]() пространства ставится в соответствие вектор
пространства ставится в соответствие вектор ![]() с началом в данной точке. «Допустимость» определяется областями определения функций
с началом в данной точке. «Допустимость» определяется областями определения функций ![]() , и если каждая из них определена при всех «икс», «игрек», «зет», то векторное поле будет задано во всём пространстве.
, и если каждая из них определена при всех «икс», «игрек», «зет», то векторное поле будет задано во всём пространстве.
! Обозначения: векторные поля также обозначают буквой ![]() либо
либо ![]() , а их компоненты через
, а их компоненты через ![]() либо
либо ![]() соответственно.
соответственно.
Из вышесказанного давно и очевидно следует, что, по меньшей мере математически, скалярные и векторные поля можно определить и во всём пространстве. Однако с соответствующими физическими примерами я всё же поостерёгся, поскольку таких понятий, как температура, гравитация (или других) ведь где-то может и вовсе не существовать. Но это уже не ужасы, а научная фантастика =) И не только фантастика. Ибо внутри камней ветер, как правило, не дует.
Следует отметить, что векторные поля (те же поля скоростей) с течением времени могут меняться, и поэтому во многих физических моделях рассматривают дополнительную независимую переменную ![]() . Кстати, то же самое касается и скалярных полей – температура же, в самом деле, тоже не «застыла» во времени.
. Кстати, то же самое касается и скалярных полей – температура же, в самом деле, тоже не «застыла» во времени.
Однако в рамках математики мы ограничимся троицей ![]() , и при «встрече» таких полей будем подразумевать некоторый фиксированный момент времени либо время, за которое поле не успело измениться.
, и при «встрече» таких полей будем подразумевать некоторый фиксированный момент времени либо время, за которое поле не успело измениться.
Векторные линии
Если скалярные поля описываются линиями и поверхностями уровня, то «форму» векторного поля можно охарактеризовать векторными линиями. Наверное, многие помнят этот школьный опыт: под лист бумаги помещаются магнит, а наверх (смотрим!) высыпаются железные опилки, которые как раз и «выстраиваются» по линиям поля.
Постараюсь сформулировать попроще: каждая точка векторной линии является началом вектора поля, который лежит на касательной в данной точке:
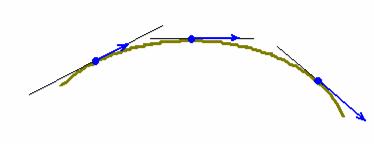
Разумеется, векторы линии в общем случае имеют разную длину, так на приведённом рисунке, при перемещении слева направо их длина растёт – здесь можно предположить, что мы приближаемся, например, к магниту. В силовых физических полях векторные линии так и называют – силовыми линиями. Другой, более простой пример – это гравитационное поле Земли: его силовые линии представляют собой лучи с началом в центре планеты, причём векторы силы тяжести расположены прямо на самих лучах.
Векторные линии скоростных полей называются линиями тока. Множество линий тока даёт нам представление о потоке жидкости или газа в данный момент времени. К слову, линия тока и траектория движения частицы – это не одно и то же. Если поле скоростей не меняется с течением времени (например, река с устоявшимся течением), то, да – мусоринки будут плыть по линиям тока. Такое поле называют стационарным, и в нём траектории движения частиц совпадают с линиями тока. Но представьте пыльную бурю – здесь линии тока в каждый момент разные, и поэтому мусоринка будет лететь по своей уникальной траектории, а вовсе не по какой-то конкретной линии тока.
Вообще, многие понятия теории поля пришли из гидродинамики, с чем мы ещё не раз столкнёмся.
Если «плоское» векторное поле задано ненулевой функцией ![]() , то его силовые линии можно найти из дифференциального уравнения
, то его силовые линии можно найти из дифференциального уравнения ![]() . Решение
. Решение ![]() данного уравнения задаёт семейство векторных линий на плоскости
данного уравнения задаёт семейство векторных линий на плоскости ![]() . Иногда в задачах требуется изобразить несколько таких линий, что обычно не вызывает затруднений – выбрали несколько удобных значений «цэ», начертили какие-нибудь там гиперболы, и порядок.
. Иногда в задачах требуется изобразить несколько таких линий, что обычно не вызывает затруднений – выбрали несколько удобных значений «цэ», начертили какие-нибудь там гиперболы, и порядок.
С пространственным векторным полем ![]() ситуация занятнее. Его силовые линии определяются соотношениями
ситуация занятнее. Его силовые линии определяются соотношениями ![]() . Здесь нужно решить систему двух дифференциальных уравнений и получить два семейства
. Здесь нужно решить систему двух дифференциальных уравнений и получить два семейства ![]() пространственных поверхностей. Линии пересечения этих семейств и будут пространственными векторными линиями. Если все компоненты («пэ», «ку», «эр») отличны от нуля, то существует несколько технических способов решения. Я не буду рассматривать все эти способы (т.к. статья разрастется до неприличных размеров), а остановлюсь на распространённом частном случае, когда одна из компонент векторного поля равна нулю. Давайте сразу распишем все варианты:
пространственных поверхностей. Линии пересечения этих семейств и будут пространственными векторными линиями. Если все компоненты («пэ», «ку», «эр») отличны от нуля, то существует несколько технических способов решения. Я не буду рассматривать все эти способы (т.к. статья разрастется до неприличных размеров), а остановлюсь на распространённом частном случае, когда одна из компонент векторного поля равна нулю. Давайте сразу распишем все варианты:
если ![]() , то нужно решить систему
, то нужно решить систему 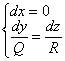 ;
;
если ![]() , то систему
, то систему 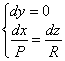 ;
;
и если ![]() , то
, то 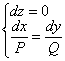 .
.
И что-то непозволительно давно у нас не было практики:
Пример 1
Найти силовые линии векторного поля ![]()
Решение: в данной задаче ![]() , поэтому решаем систему:
, поэтому решаем систему:
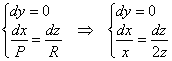
Первый диффур вообще халява:
![]()
![]() – семейство плоскостей, параллельных координатной плоскости
– семейство плоскостей, параллельных координатной плоскости ![]() (представили в уме!).
(представили в уме!).
Второй диффур – почти она же:), ну а зачем нам скоропостижные трудности?
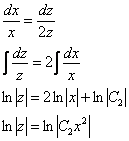
![]() – семейство (внимание!) параболических цилиндров, параллельных оси
– семейство (внимание!) параболических цилиндров, параллельных оси ![]() .
.
Ответ: искомое множество векторных линий: 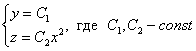
Иными словами, здесь в каждой плоскости ![]() «сидит» семейство парабол
«сидит» семейство парабол ![]() .
.
Аналогичная задачка для самостоятельного решения:
Пример 2
Найти силовые линии векторного поля ![]()
Охарактеризуйте получившееся множество линий. Кстати, в условии явно не сказано, о каком поле идёт речь – плоском или пространственном. В подобных ситуациях рекомендую решать задачу для пространства – не ошибётесь ;-)
Краткое решение и ответ в конце урока.
Векторное поле градиентов
В каких отношениях вы находитесь с производной по направлению и градиентом? …ничего страшного, от ненависти до любви – один шаг =) Напоминаю, что градиент функции в точке – это несвободный вектор, указывающий направление максимального роста функции в данной точке и определяющий скорость этого роста.
Нахождение векторной функции градиентов – есть популярный и распространённый способ получить из скалярного поля поле векторное. При условии существования соответствующих частных производных функции двух и трёх переменных:
![]()
![]()
Смысл очень прост. Так, если функция ![]() задаёт скалярное поле глубины озера, то соответствующая векторная функция
задаёт скалярное поле глубины озера, то соответствующая векторная функция ![]() определяет множество несвободных векторов, каждый из которых указывает направление наискорейшего подъёма дна в той или иной точке
определяет множество несвободных векторов, каждый из которых указывает направление наискорейшего подъёма дна в той или иной точке ![]() и скорость этого подъёма.
и скорость этого подъёма.
Если функция ![]() задаёт скалярное поле температуры некоторой области пространства, то соответствующее векторное поле
задаёт скалярное поле температуры некоторой области пространства, то соответствующее векторное поле ![]() характеризует направление и скорость наибыстрейшего прогревания пространства в каждой точке
характеризует направление и скорость наибыстрейшего прогревания пространства в каждой точке ![]() этой области.
этой области.
Разберём общую математическую задачу:
Пример 3
Дано скалярное поле ![]() и точка
и точка ![]() . Требуется:
. Требуется:
1) составить градиентную функцию скалярного поля;
2) найти градиент поля в точке ![]() и вычислить его длину;
и вычислить его длину;
3) вычислить производную по направлению нормального вектора к поверхности ![]() в точке
в точке ![]() , образующего с положительной полуосью
, образующего с положительной полуосью ![]() тупой угол.
тупой угол.
Непосредственно к решению задачи это не относится, но сразу обратим внимание, что скалярное поле не определено на всех трёх координатных плоскостях ![]() .
.
1) Быстренько вспоминаем, как находить частные производные функции трёх переменных:
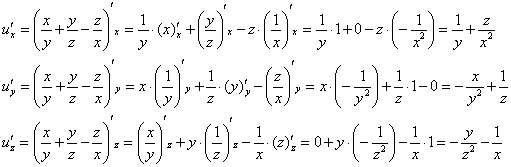
Составим функцию, которая определяет векторное поле градиентов:
![]()
И ещё раз – в чём её смысл? Полученная векторная функция каждой точке ![]() области определения скалярного поля ставит в соответствие вектор
области определения скалярного поля ставит в соответствие вектор ![]() , указывающий направление и максимальную скорость роста функции
, указывающий направление и максимальную скорость роста функции ![]() в данной точке.
в данной точке.
И один из таких векторов нам предстоит найти в следующем пункте:
2) Вычислим частные производные в точке ![]() :
:
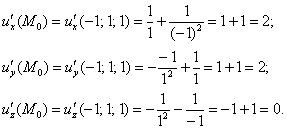
Таким образом:
![]() – ещё раз подчёркиваю, что этот вектор исходит из точки
– ещё раз подчёркиваю, что этот вектор исходит из точки ![]() , и перемещать его никуда нельзя! По той причине, что он характеризует направление наискорейшего возрастания функции
, и перемещать его никуда нельзя! По той причине, что он характеризует направление наискорейшего возрастания функции ![]() именно в точке «эм нулевое», а не где-то ещё!
именно в точке «эм нулевое», а не где-то ещё!
Мерилом же этой максимальной скорости как раз является длина градиента:
![]()
3) Вычислим производную по направлению нормального вектора к поверхности ![]() в точке
в точке ![]() , образующего с положительной полуосью
, образующего с положительной полуосью ![]() тупой угол.
тупой угол.
Немного мудрёно, но разобраться немудренО. Во-первых, убедимся, что точка «эм нулевое» действительно принадлежит данной поверхности:
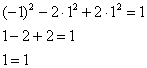
Получено верное равенство. ОК.
Что это за поверхность – нас не интересует, нам важен её нормальный вектор в точке ![]() , да не абы какой, а образующий с полуосью
, да не абы какой, а образующий с полуосью ![]() тупой угол.
тупой угол.
Вспоминаем материал ещё одного урока: вектор нормали к поверхности ![]() в точке
в точке ![]() задаётся следующим образом:
задаётся следующим образом:
![]()
В данном случае:
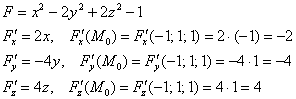
![]()
Но нужный ли это вектор? Как выяснить угол, который он образует с полуосью ![]() ? …Сегодня у нас какой-то экскурс в фильмы… =) и сейчас на очереди фильм «Вспомнить всё». Вычислим скалярное произведение вектора
? …Сегодня у нас какой-то экскурс в фильмы… =) и сейчас на очереди фильм «Вспомнить всё». Вычислим скалярное произведение вектора ![]() с направляющим вектором
с направляющим вектором ![]() положительной «зетовой» полуоси:
положительной «зетовой» полуоси:
![]() , следовательно, угол между этими векторами острый, что нас не устраивает!
, следовательно, угол между этими векторами острый, что нас не устраивает!
И поэтому нужно выбрать противоположно направленный нормальный вектор:
![]()
Заметим заодно, что нормальные векторы в отличие от градиентов – свободны, их задача лишь указать направление.
Вычислим направляющие косинусы данного направления, или, что то же самое – координаты единичного вектора, сонаправленного с вектором ![]() :
:
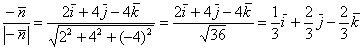
Контроль: 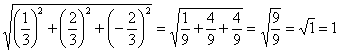
![]()
Таким образом, искомая производная по направлению:
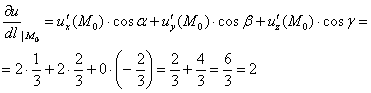
Напоминаю, что это значение характеризует скорость роста функции ![]() в точке
в точке ![]() по направлению вектора
по направлению вектора ![]() , и оно не может оказаться больше, чем
, и оно не может оказаться больше, чем ![]() (максимальной скорости роста в данной точке).
(максимальной скорости роста в данной точке).
Ответ:
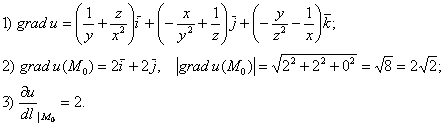
Небольшой пример для самостоятельного решения:
Пример 4
Найти угол между градиентами скалярных полей ![]() и
и ![]() в точке
в точке ![]()
Просто и со вкусом. …Как найти угол? – с помощью того же скалярного произведения. Ну и, очевидно, тут придётся «тряхнуть» многоэтажными дробями и некоторой тригонометрией. Краткое решение и ответ в конце урока.
Что делать, если вам предложено «плоское» скалярное поле ![]() ? Просто убавьте одну координату, соответствующие примеры можно найти в статье Производная по направлению и градиент функции. По существу, мы вновь прорешали примеры той статьи, только немного в другой интерпретации.
? Просто убавьте одну координату, соответствующие примеры можно найти в статье Производная по направлению и градиент функции. По существу, мы вновь прорешали примеры той статьи, только немного в другой интерпретации.
Потенциальное векторное поле
На уроке Криволинейный интеграл по замкнутому контуру я уже подробно рассказал о «плоском» потенциальном поле, и поэтому перед дальнейшим чтением будет крайне полезно окинуть взглядом концовку указанной статьи. Фактически сейчас будет продолжение, где мы разбёрём аналогичную ситуацию в пространстве.
«Потенциальное»…, на ум здесь приходит потенциальная энергия, потенциальные возможности. Так, лежащий на подоконнике кирпич потенциально можно сбросить вниз, и вмятина на земле неиллюзорно продемонстрируют нам ту самую потенциальную энергию. Всё верно, гравитационное поле Земли – это один из ярких примеров потенциального векторного поля.
Вспомним его характерный признак, сбросив с подоконника нашего уютного деревенского домика…, нет, не кирпич, а пёрышко. Из точки ![]() до точки
до точки ![]() оно может пролететь по бесчисленному множеству траекторий (из-за ветра, по причине сопротивления воздуха и т.д.), но во всех случаях гравитационное поле Земли совершит одну и ту же работу по перемещению пера между этими точками. Ну а различные траектории – это уже «вклад» других сил, которые, к слову, тоже можно описать векторными полями.
оно может пролететь по бесчисленному множеству траекторий (из-за ветра, по причине сопротивления воздуха и т.д.), но во всех случаях гравитационное поле Земли совершит одну и ту же работу по перемещению пера между этими точками. Ну а различные траектории – это уже «вклад» других сил, которые, к слову, тоже можно описать векторными полями.
Примечание: возможно, здесь у вас возник вопрос: «но ветер же может приподнимать перо, и тогда работа должна увеличиваться!». Ничего подобного. Физическое понятие работы не подразумевает, что кто-то или что-то «трудится». Если ветер приподнимает перо вверх, то он просто уменьшает абсолютную величину работы силы тяжести.
В физике есть конкретная математическая модель, описывающая гравитационные силы, но в соответствии с направленностью сайта, я приведу только общие формулы. Итак:
Векторное поле ![]() является потенциальным, если оно представляет собой поле градиентов некоторого скалярного поля
является потенциальным, если оно представляет собой поле градиентов некоторого скалярного поля ![]() . Функцию
. Функцию ![]() называют потенциальной функцией или просто потенциалом.
называют потенциальной функцией или просто потенциалом.
Работа ![]() потенциального векторного поля по перемещению материальной точки из точки
потенциального векторного поля по перемещению материальной точки из точки ![]() в точку
в точку ![]() не зависит от траектории её движения и выражается следующим криволинейным интегралом 2-го рода:
не зависит от траектории её движения и выражается следующим криволинейным интегралом 2-го рода:
![]() , который равен разности потенциалов
, который равен разности потенциалов ![]() .
.
Иными словами, в потенциальном поле имеет значение лишь начальная и конечная точка маршрута. И если эти точки совпадают, то суммарная работа сил по замкнутому контуру ![]() будет равна нулю:
будет равна нулю:
![]()
Давайте поднимем пёрышко с земли и доставим его в исходную точку. При этом траектория нашего движения опять же произвольная; можно даже бросить перо, снова его поднять и т.д.
Почему итоговый результат нулевой?
Перо упало из точки «а» в точку «бэ»? Упало. Сила тяжести совершила работу ![]() .
.
Перо попало обратно в точку «а»? Попало. А это значит, что была совершена точно такая же работа ![]() против сил тяжести, причём не важно с какими «приключениями» и какими силами – да хоть ветер задул его обратно.
против сил тяжести, причём не важно с какими «приключениями» и какими силами – да хоть ветер задул его обратно.
Примечание: в физике знак «минус» символизирует противоположное направление.
Таким образом, суммарная работа сил равна нулю: ![]()
Как я уже отмечал, физическое и обывательское понятие работы отличаются. И это различие вам хорошо поможет понять не пёрышко и даже не кирпич, а, например, пианино :)
Дружно поднимите пианино и спустите его по лестнице вниз. Потаскайте по улице. Сколько захочется и где захочется. И если никто не вызвал дурку занесите инструмент обратно. Вы поработали? Конечно. До седьмого пота. Но с точки зрения физики никакой работы не совершено.
Словосочетание «разность потенциалов» подмывает рассказать ещё о потенциальном электростатическом поле, но бить током своих читателей как-то уж совсем не гуманно =) Тем более, примеров – непочатый край, ибо потенциальным является любое градиентное поле, коих пруд пруди.
Но легко сказать «пруд пруди»: вот дано нам векторное поле ![]() – как определить, потенциально оно или нет?
– как определить, потенциально оно или нет?
Ротор векторного поля
Или его вихревая составляющая, которая тоже выражается векторами.
Снова возьмём в руки пёрышко и аккуратно отправим его в плавание по реке. Для чистоты эксперимента будем считать, что оно однородно и симметрично относительно своего центра. Ось ![]() торчит вверх.
торчит вверх.
Рассмотрим векторное поле скорости течения (считаем, что оно неизменно во времени), и некоторую точку водной поверхности, над которой находится центр пера.
Если в данной точке перо вращается против часовой стрелки, то поставим ей в соответствие исходящий несвободный вектор, направленный вверх. При этом, чем быстрее вращается перо, тем длиннее этот вектор, …мне почему-то он представляется таким чёрным-чёрным в ярких лучах солнца…. Если вращение происходит ПО часовой стрелке, то вектор «смотрит» вниз. Если же перо не вращается вовсе, то вектор нулевой.
Знакомьтесь – это и есть вектор ротора векторного поля скорости, он характеризует направление «завихрения» жидкости в данной точке и угловую скорость вращения пера (но не направление и не скорость самого течения!).
Совершенно понятно, что роторный вектор есть у всех точек реки (в том числе тех, которые «под водой»), таким образом, для векторного поля скорости течения мы определили новое векторное поле!
Если векторное поле задано функцией ![]() , то его роторное поле задаётся следующей векторной функцией:
, то его роторное поле задаётся следующей векторной функцией:
![]()
При этом, если векторы роторного поля реки велики по модулю и имеют тенденцию менять направление, то это вовсе не означает, что речь идёт об извилистой и неспокойной реке (возвращаемся к примеру). Такая ситуация может наблюдаться и в прямолинейном русле – когда, например, в середине скорость выше, а у берегов ниже. То есть, вращение пера порождается различными скоростями течения в соседних линиях тока. Но это не единственно возможная причина вращения. Если рядом с рекой стоит экспериментатор и поливает её из шланга, то поле скоростей будет постоянно меняться, и «завихрения» начнутся по той причине, что меняются сами линии тока.
С другой стороны, если роторные векторы коротки, то это может быть и «петляющая» горная речка! Важно, чтобы в соседних линиях тока скорость самого течения (быстрого или медленного) отличалась незначительно. И не было рядом экспериментаторов или каких-нибудь оползней, которые меняют поле скоростей.
И, наконец, отвечаем на поставленный выше вопрос: в любой точке потенциального поля ![]() его ротор равен нулю:
его ротор равен нулю:
![]() , а точнее, нулевому вектору.
, а точнее, нулевому вектору.
Потенциальное поле также называют безвихревым полем.
«Идеального» течения, конечно, не существует, но довольно часто можно наблюдать, что поле скорости реки близкО к потенциальному – плывут себе спокойно разные предметы и не вертятся, ...вы тоже представили эту картинку? Однако, плыть они могут и очень быстро, и по кривой, и то замедляться, то ускоряться – важно чтобы скорость течения в соседних линиях тока сохранялась постоянной и сами линии тока оставались неизменными.
Ну и, конечно, наше бренное гравитационное поле. Для следующего опыта хорошо подойдёт любой достаточно тяжёлый и однородный предмет, например, закрытая книга, непочатая банка пива или, кстати, кирпич, который таки дождался своего часа =) Зажмите его торцы руками, приподнимите вверх и аккуратно отпустите в свободное падение. Крутиться он не будет. А если и будет, то это уже ваши «личные усилия» или кирпич попался неправильный. Не поленитесь и проверьте этот факт! Только не бросайте ничего из окна, это уже не перо
После чего с чистой совестью и повышенным тонусом можно вернуться к практическим задачам:
Пример 5
Показать, что векторное поле ![]() является потенциальным и найти его потенциал
является потенциальным и найти его потенциал
![]()
Решение: условие прямо утверждает потенциальность поля, и наша задача состоит в доказательстве этого факта. Найдём роторную функцию или, как чаще говорят – ротор данного поля:
![]()
Для удобства выпишем компоненты поля:
![]()
и начнём находить их частные производные – их удобно «перебирать» в «роторном» порядке, слева направо:
![]() – и сразу проверяем, что
– и сразу проверяем, что ![]() (чтобы не выполнять лишней работы в случае ненулевого результата). Едем дальше:
(чтобы не выполнять лишней работы в случае ненулевого результата). Едем дальше:
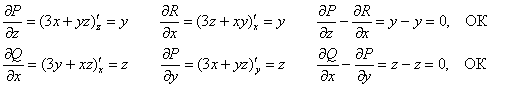
Таким образом:
![]() , следовательно, поле
, следовательно, поле ![]() потенциально, а значит, представляет собой градиентную функцию
потенциально, а значит, представляет собой градиентную функцию ![]() некоторого скалярного поля, заданного потенциалом
некоторого скалярного поля, заданного потенциалом ![]() .
.
Функцию ![]() обычно находят одним из следующих способов:
обычно находят одним из следующих способов:
1) Способ первый. Коль скоро так (см. выше), то:
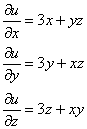
Дальнейший алгоритм напоминает решение дифференциального уравнения в полных дифференциалах, только с бОльшим количеством шагов:
Так как ![]() , то:
, то:
![]() , где
, где ![]() – пока ещё неизвестная функция, зависящая от «игрек» и «зет».
– пока ещё неизвестная функция, зависящая от «игрек» и «зет».
Дифференцируем полученный результат по «игрек»:
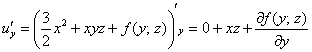
Но, с другой стороны ![]() . Приравниваем и упрощаем:
. Приравниваем и упрощаем:
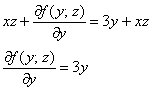
Теперь частным интегрированием (переменных здесь уже две!) находим:
![]() – подставляем в наш первый трофей
– подставляем в наш первый трофей ![]() :
:
![]() , после чего дифференцируем его уже по «зет»:
, после чего дифференцируем его уже по «зет»:
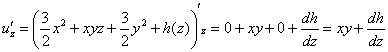
Но с другой стороны, ![]() . Приравниваем и упрощаем:
. Приравниваем и упрощаем:
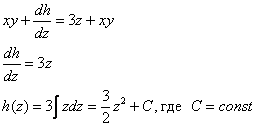
И, наконец, подставляем найдённую функцию ![]() в наш «усовершенствованный трофей»
в наш «усовершенствованный трофей» ![]() :
:
![]() – получаем тем самым, искомую потенциальную функцию.
– получаем тем самым, искомую потенциальную функцию.
Проверку тут выполнить легче лёгкого, находим частные производные 1-го порядка:
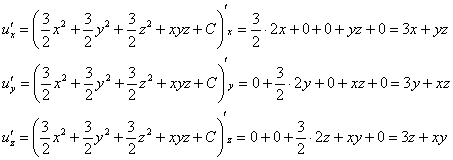
которые совпали с соответствующими компонентами исходного поля ![]() , в чём и требовалось убедиться.
, в чём и требовалось убедиться.
Ну и, наверное, некоторые уже подметили, что равенства частных производных в «роторной» формуле – есть не что иное, как равенства смешанных частных производных 2-го порядка функции ![]() .
.
2) Способ второй. Потенциальную функцию можно найти при помощи формулы:
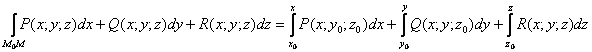 , где
, где ![]() – точка с переменными координатами, а
– точка с переменными координатами, а ![]() – некоторая фиксированная точка скалярного поля
– некоторая фиксированная точка скалярного поля ![]() .
.
Легко видеть, что этот криволинейный интеграл определяет работу векторного поля ![]() от точки
от точки ![]() до точки
до точки ![]() и численно равен разности потенциалов
и численно равен разности потенциалов ![]() , откуда, собственно, и получается нужная функция
, откуда, собственно, и получается нужная функция ![]()
Запишем сумму трёх интегралов для поля ![]() :
:

И на этом шаге я по возможности рекомендую выбрать точку ![]() (если функция
(если функция ![]() и её производные в ней определены). После чего решение значительно упрощается:
и её производные в ней определены). После чего решение значительно упрощается:

При подстановке верхних пределов интегрирования можно сказать, что вместо «икс» мы подставляем «икс», вместо «игрек» – «игрек», и вместо «зет» – «зет».
Ответ: ![]()
Если начало координат выбрать нельзя, то задачу придётся решать в общем виде, в результате чего должна получиться разность ![]() . Любители трудностей могут вернуться к примеру и прийти к разности
. Любители трудностей могут вернуться к примеру и прийти к разности ![]() . Разумеется, это легальный и рабочий вариант – можно решать и так.
. Разумеется, это легальный и рабочий вариант – можно решать и так.
С аналогичной задачей для «плоского» векторного поля можно ознакомиться на уроке Криволинейный интеграл по замкнутому контуру.
Пара полей для самостоятельного решения:
Пример 6
Выяснить, являются ли следующие векторные поля потенциальными, и если да, то найти их потенциалы:
а) ![]()
б) ![]()
Обязано ли поле быть потенциальным в таких задачах? Конечно, нет, и отрицательный ответ – это тоже полноценный ответ. Примерный образец чистового оформления заданий внизу страницы.
Ну что же, теперь пришло время немного отдохнуть и увеличить ротор реки =) А именно нырнуть, искупаться и позагорать на солнце. Чтобы с новыми силами вернуться к столь увлекательной теме, а именно к потоку и циркуляции векторного поля
Спасибо за внимание и до скорых встреч!
Решения и ответы:
Пример 2: Решение: составим и решим систему:
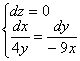
Из 1-го уравнения:
![]()
Из 2-го уравнения:
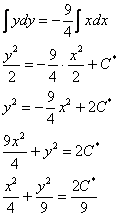
Константу ![]() переобозначим через
переобозначим через ![]()
Ответ: 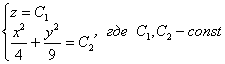 – семейства эллипсов, расположенные в плоскостях
– семейства эллипсов, расположенные в плоскостях ![]() , параллельных плоскости
, параллельных плоскости ![]() .
.
Примечание: если в условии задачи подразумевается «плоское» векторное поле, то векторные линии представляют собой множество эллипсов ![]() , расположенных в плоскости
, расположенных в плоскости ![]() .
.
Пример 4: Решение: вычислим частные производные функции ![]() в точке
в точке ![]() :
:
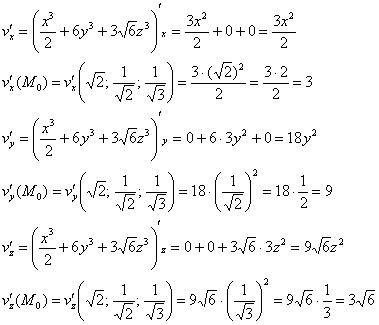
Составим градиент данного скалярного поля в точке ![]() и вычислим его длину:
и вычислим его длину:
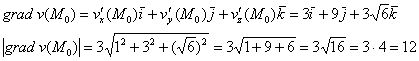
Аналогично найдём градиент второго скалярного поля:
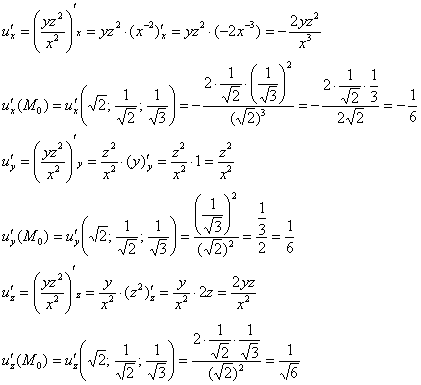
В результате:
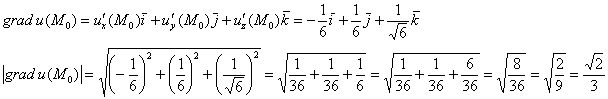
Угол ![]() между градиентами найдём по формуле:
между градиентами найдём по формуле:
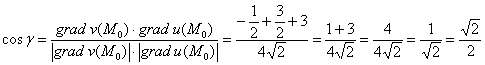
Таким образом:
![]()
Ответ: ![]()
Пример 6: Решение:
а) проверим, равен ли нулю ротор векторного поля:
![]() .
.
В данном случае:
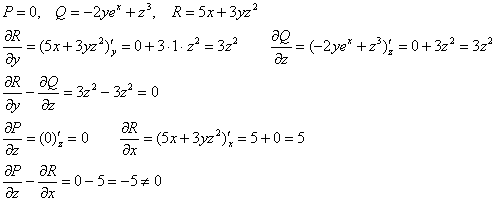
Следовательно, ![]()
Ответ: поле ![]() не потенциально.
не потенциально.
б) найдём ротор векторного поля:
![]()
В данной задаче:
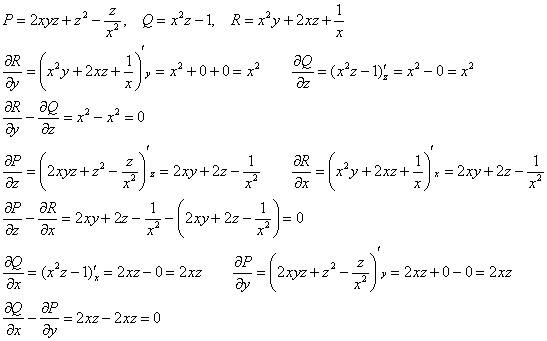
Таким образом: ![]() , значит, поле
, значит, поле ![]() потенциально и представляет собой функцию градиента
потенциально и представляет собой функцию градиента ![]() некоторого скалярного поля
некоторого скалярного поля ![]() . Найдём этот потенциал (здесь выгоднее использовать 1-й способ):
. Найдём этот потенциал (здесь выгоднее использовать 1-й способ):
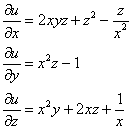
Так как ![]() , то:
, то:
![]()
Дифференцируем по «игрек»:
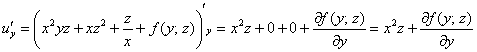
С другой стороны ![]() . Таким образом:
. Таким образом:
![]()
![]() – подставим в
– подставим в ![]() :
:
![]()
Дифференцируем по «зет»:
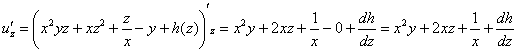
С другой стороны, ![]() . Таким образом:
. Таким образом:
![]()
![]() – подставим в
– подставим в ![]()
Ответ: поле ![]() потенциально,
потенциально, ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
