
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Знакочередующиеся ряды. Признак Лейбница.
Абсолютная и условная сходимость
Для того чтобы понять примеры данного урока необходимо хорошо ориентироваться в положительных числовых рядах: понимать, что такое ряд, знать необходимый признак сходимости ряда, уметь применять признаки сравнения, признак Даламбера, признаки Коши. Тему можно поднять практически с нуля, последовательно изучив статьи Ряды для чайников и Признак Даламбера. Признаки Коши. Логически этот урок является третьим по счёту, и он позволит не только разобраться в знакочередующихся рядах, но и закрепить уже пройденный материал! Какой-то новизны будет немного, и освоить знакочередующиеся ряды не составит большого труда. Всё просто и доступно.
Что такое знакочередующийся ряд? Это понятно или почти понятно уже из самого названия. Сразу простейший пример.
Рассмотрим ряд ![]() и распишем его подробнее:
и распишем его подробнее:
![]()
А сейчас будет убийственный комментарий. У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.
Знакочередование обеспечивает множитель ![]() : если
: если ![]() чётное, то будет знак «плюс», если нечётное – знак «минус» (как вы помните ещё с урока о числовых последовательностях, эта штуковина называется «мигалкой»). Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».
чётное, то будет знак «плюс», если нечётное – знак «минус» (как вы помните ещё с урока о числовых последовательностях, эта штуковина называется «мигалкой»). Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».
В практических примерах знакочередование членов ряда может обеспечивать не только множитель ![]() , но и его родные братья:
, но и его родные братья: ![]() ,
, ![]() ,
, ![]() , …. Например:
, …. Например:
![]()
Подводным камнем являются «обманки»: ![]() ,
, ![]() ,
, ![]() и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном
и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном ![]() :
: ![]() ,
, ![]() ,
, ![]() . Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решения функциональных рядов.
. Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решения функциональных рядов.
Как исследовать знакочередующийся ряд на сходимость? Использовать признак Лейбница. Про немецкого гиганта мысли Готфрида Вильгельма Лейбница я рассказывать ничего не хочу, так как помимо математических трудов, он накатал несколько томов по философии. Опасно для мозга.
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.
Или в два пункта:
1) Ряд является знакочередующимся.
2) Члены ряда убывают по модулю: ![]() , причём, убывают монотонно.
, причём, убывают монотонно.
Если выполнены эти условия, то ряд сходится.
Краткая справка о модуле приведена в методичке Горячие формулы школьного курса математики, но для удобства ещё раз:
Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду ![]() . Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:
. Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:
– Члены ряда без учёта знака убывают.
– Члены ряда убывают по модулю.
– Члены ряда убывают по абсолютной величине.
– Модуль общего члена ряда стремится к нулю: ![]()
// Конец справки
Теперь немного поговорим про монотонность. Монотонность – это скучное постоянство.
Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий: ![]() . Для ряда
. Для ряда ![]() выполнена строгая монотонность убывания, её можно расписать подробно:
выполнена строгая монотонность убывания, её можно расписать подробно:
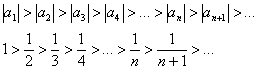
А можно сказать короче: каждый следующий член ряда по модулю меньше, чем предыдущий: ![]() .
.
Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: ![]() . Рассмотрим ряд с факториалом:
. Рассмотрим ряд с факториалом: ![]() Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего:
Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего: ![]() .
.
В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая).
Кроме того, члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим. Это очевидное следствие, которое в некоторых источниках добавляют к «классической» формулировке признака.
Не нужно пугаться того, что я нагородил, практические примеры всё расставят по своим местам:
Пример 1
Исследовать ряд на сходимость ![]()
В общий член ряда входит множитель ![]() , и это наталкивает на естественную мысль проверить выполнение условий признака Лейбница:
, и это наталкивает на естественную мысль проверить выполнение условий признака Лейбница:
1) Проверка ряда на знакочередование. Обычно в этом пункте решения ряд расписывают подробно ![]() и выносят вердикт «Ряд является знакочередующимся».
и выносят вердикт «Ряд является знакочередующимся».
2) Убывают ли члены ряда по модулю? Здесь нужно решить предел ![]() , который чаще всего является очень простым.
, который чаще всего является очень простым.
![]() – члены ряда не убывают по модулю, и из этого автоматически следует его расходимость – по той причине, что предела
– члены ряда не убывают по модулю, и из этого автоматически следует его расходимость – по той причине, что предела ![]() не существует *, то есть, не выполнен необходимый признак сходимости ряда.
не существует *, то есть, не выполнен необходимый признак сходимости ряда.
* Согласно, строгому определению предела числовой последовательности, и кроме того, в данном случае это очевидно.
Вывод: ряд расходится.
Как разобраться, чему равно ![]() ? Очень просто. Как известно, модуль уничтожает минусы, поэтому для того, чтобы составить
? Очень просто. Как известно, модуль уничтожает минусы, поэтому для того, чтобы составить ![]() , нужно просто убрать с крыши проблесковый маячок. В данном случае общий член ряда
, нужно просто убрать с крыши проблесковый маячок. В данном случае общий член ряда ![]() . Тупо убираем «мигалку»:
. Тупо убираем «мигалку»: ![]() .
.
Пример 2
Исследовать ряд на сходимость ![]()
Используем признак Лейбница:
1) ![]()
Ряд является знакочередующимся.
2) ![]() – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий:
– члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: ![]() (
(![]() ) – поскольку бОльшим знаменателям соответствуют мЕньшие дроби. Таким образом, убывание монотонно.
) – поскольку бОльшим знаменателям соответствуют мЕньшие дроби. Таким образом, убывание монотонно.
Вывод: ряд сходится.
Однако это еще не всё! Сходимость бывает разной. А именно:
– сходящийся ряд ![]() называют абсолютно сходящимся, если сходится ряд
называют абсолютно сходящимся, если сходится ряд ![]() ;
;
в противном случае ряд ![]() сходится условно.
сходится условно.
! Из вышесказанного очевидно следует, что любой сходящийся положительный ряд является абсолютно сходящимся.
Поэтому в типовом задании, как правило, нужно провести второй этап решения. ...Не виноватый я – такая уж теория и практика числовых рядов =)
Составим ряд из модулей – опять просто убираем множитель, который обеспечивает знакочередование:
![]() – расходится (гармонический ряд) – тут даже без исследования обошлось.
– расходится (гармонический ряд) – тут даже без исследования обошлось.
Таким образом, наш ряд ![]() сходится условно.
сходится условно.
Следует отметить, что при формулировке «Исследуйте ряд на сходимость» можно рискнуть и ограничиться признаком Лейбница (т.е. просто констатировать сходимость), но таки лучше не лениться – с большой вероятностью вас попросят уточнить, сходится ли ряд абсолютно или условно.
Заметьте также, что в Примере 1 второй этап по-любому отпадает, поскольку еще на первом шаге сделан вывод о том, что ряд расходится.
Собираем ведёрки, лопатки, машинки и выходим из песочницы, чтобы смотреть на мир широко открытыми глазами из кабины моего экскаватора:
Пример 3
Исследовать ряд на сходимость ![]()
Используем признак Лейбница:
1) ![]()
Данный ряд является знакочередующимся.
2) ![]() – члены ряда убывают по модулю.
– члены ряда убывают по модулю.
Для любого номера ![]() справедливо неравенство:
справедливо неравенство: ![]() , а бОльшим знаменателям соответствуют меньшие дроби:
, а бОльшим знаменателям соответствуют меньшие дроби:
![]() , то есть, каждый следующий член ряда по модулю меньше, чем предыдущий:
, то есть, каждый следующий член ряда по модулю меньше, чем предыдущий: ![]() , а это означает, что убывание монотонно.
, а это означает, что убывание монотонно.
Вывод: ряд сходится.
Теперь выясним, как именно. Для этого составим и исследуем соответствующий ряд из модулей:
![]()
Анализируя начинку, приходим к выводу, что здесь нужно использовать предельный признак сравнения. Скобки в знаменателе удобнее раскрыть:
![]()
Сравним данный ряд со сходящимся рядом ![]() . Используем предельный признак сравнения.
. Используем предельный признак сравнения.
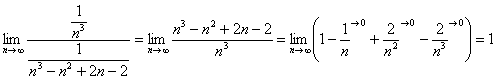
Получено конечное число, отличное от нуля, значит, ряд ![]() сходится вместе с рядом
сходится вместе с рядом ![]() .
.
Таким образом, ряд ![]() сходится абсолютно.
сходится абсолютно.
Готово.
Пример 4
Исследовать ряд на сходимость ![]()
Пример 5
Исследовать ряд на сходимость ![]()
Это примеры для самостоятельного решения. Полное решение и образец оформления в конце урока.
Как видите, знакочередующиеся ряды – это просто и занудно! Но не спешите закрывать страницу, всего через пару экранов мы рассмотрим случай, который многих ставит в тупик. А пока еще пара примеров для тренировки и повторения.
Пример 6
Исследовать ряд на сходимость ![]()
Используем признак Лейбница:
1) Ряд является знакочередующимся.
2) 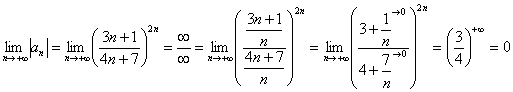 – члены ряда убывают по модулю. Осталось показать монотонность убывания. Неравенство
– члены ряда убывают по модулю. Осталось показать монотонность убывания. Неравенство ![]() здесь обосновать трудно и поэтому мы проявим разумную хитрость, расписав несколько конкретных членов и всю цепочку:
здесь обосновать трудно и поэтому мы проявим разумную хитрость, расписав несколько конкретных членов и всю цепочку:
![]()
![]() – не лишним будет взять в руки калькулятор, и убедиться в справедливости первых неравенств (хотя, это, конечно, некорректная проверка).
– не лишним будет взять в руки калькулятор, и убедиться в справедливости первых неравенств (хотя, это, конечно, некорректная проверка).
Вывод: ряд сходится.
Обратите внимание, что я не расписал подробно члены ряда. Их всегда желательно расписывать, но от непреодолимой лени в «тяжелых» случаях можно ограничиться фразой «Ряд является знакочередующимся». Кстати, не нужно относиться к этому пункту формально, всегда проверяем (хотя бы мысленно) что ряд действительно знакочередуется. Помните об «обманках» ![]() ,
, ![]() ,
, ![]() – если они есть, то от них нужно избавиться, получив «обычный» ряд с положительными членами.
– если они есть, то от них нужно избавиться, получив «обычный» ряд с положительными членами.
Выясним характер сходимости ряда:
![]()
Очевидно, что нужно использовать радикальный признак Коши:
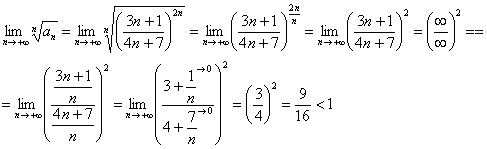
Таким образом, ряд ![]() сходится.
сходится.
Исследуемый ряд сходится абсолютно.
Пример 7
Исследовать ряд на сходимость ![]()
Это пример для самостоятельного решения. Хммм… что-то я немного погорячился на счет простоты.
Нередко встречаются знакочередующиеся ряды, которые вызывают затруднения.
Пример 8
Исследовать ряд на сходимость ![]()
Используем признак Лейбница:
1) Ряд является знакочередующимся.
2) ![]()
Дело в том, что не существует стандартных обыденных приемов для решения подобных пределов. Куда стремится такой предел? К нулю, к бесконечности? Здесь важно знать, ЧТО на бесконечности растёт быстрее – числитель или знаменатель.
Примечание: понятие порядка роста функции подробно освещено в статье Методы решения пределов. У нас пределы последовательностей, но это не меняет сути.
Если числитель ![]() при
при ![]() растёт быстрее факториала, то
растёт быстрее факториала, то ![]() . Если, на бесконечности факториал растёт быстрее числителя, то он, наоборот – «утянет» предел на ноль:
. Если, на бесконечности факториал растёт быстрее числителя, то он, наоборот – «утянет» предел на ноль: ![]() . А может быть этот предел равен какому-нибудь отличному от нуля числу?
. А может быть этот предел равен какому-нибудь отличному от нуля числу?
Попробуем записать несколько первых членов ряда:
![]()
![]()
![]()
Создается стойкое впечатление, что ![]() , но где гарантия, что при очень больших «эн» факториал не «обгонит» числитель и не утащит предел на ноль?
, но где гарантия, что при очень больших «эн» факториал не «обгонит» числитель и не утащит предел на ноль?
Обратимся к теории математического анализа, для того она и существует:
Справка:
– Факториал растёт быстрее, чем показательная последовательность ![]() , иными словами:
, иными словами: ![]() или
или ![]() . Да хоть миллион в степени «эн», это не меняет дела. То есть, факториал более высокого порядка роста.
. Да хоть миллион в степени «эн», это не меняет дела. То есть, факториал более высокого порядка роста.
– Факториал растёт быстрее, чем степеннАя последовательность ![]() или многочлен, иными словами:
или многочлен, иными словами: ![]() или
или ![]() . Вместо
. Вместо ![]() можно подставить какой-нибудь многочлен тысячной степени, это опять же не изменит ситуацию – рано или поздно факториал всё равно «перегонит» и такой страшный многочлен. То есть и здесь факториал более высокого порядка роста.
можно подставить какой-нибудь многочлен тысячной степени, это опять же не изменит ситуацию – рано или поздно факториал всё равно «перегонит» и такой страшный многочлен. То есть и здесь факториал более высокого порядка роста.
– Факториал растёт быстрее произведения показательной ![]() и степенной последовательностей
и степенной последовательностей ![]() (наш случай). А также быстрее произведения и бОльшего количества таких множителей.
(наш случай). А также быстрее произведения и бОльшего количества таких множителей.
И, раз пошла такая пьянка:
– Показательная последовательность ![]() растёт быстрее, чем степенная последовательность
растёт быстрее, чем степенная последовательность ![]() , например:
, например: ![]() ,
, ![]() . Аналогично факториалу, она «перетягивает» произведение степенных последовательностей:
. Аналогично факториалу, она «перетягивает» произведение степенных последовательностей: ![]() .
.
– А есть ли что-нибудь «круче» факториала? Есть! Степенно-показательная последовательность ![]() растёт быстрее, чем
растёт быстрее, чем ![]() . На практике встречается редко, но информация лишней не будет.
. На практике встречается редко, но информация лишней не будет.
// Конец справки
Таким образом, второй пункт исследования (вы еще о нём помните? =)) можно записать так:
2) ![]() – члены ряда монотонно убывают по модулю (так как
– члены ряда монотонно убывают по модулю (так как ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() ).
).
Достаточно! О том, что члены начинают убывать лишь с некоторого номера «эн», лучше благоразумно умолчать – по той причине, что найти этот номер не так-то просто, а лишние вопросы вам ни к чему ;) Ещё труднее показать монотонность убывания, поэтому просто констатируем этот факт. Здесь вас с высокой вероятностью «простят»
Вывод: ряд сходится.
Исследуем ряд, составленный из модулей членов:
![]()
А тут уже работает старый добрый признак Даламбера:
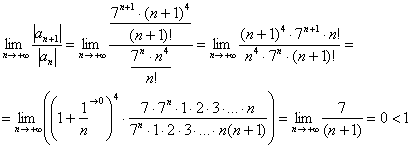
Таким образом, ряд ![]() сходится.
сходится.
Исследуемый ряд сходится абсолютно.
Разобранный пример можно решить другим способом.
Теорема: если ряд ![]() сходится, то сходится и ряд
сходится, то сходится и ряд ![]()
Пример 8 «на бис» вторым способом.
Исследовать ряд на сходимость ![]()
Решение: исследуем сходимость ряда, составленного из модулей:
![]()
Используем признак Даламбера:
…
только что печатал
…
Таким образом, ряд ![]() сходится, а значит, по соответствующей теореме, сходится и исследуемый ряд, причём, ясно как день – абсолютно.
сходится, а значит, по соответствующей теореме, сходится и исследуемый ряд, причём, ясно как день – абсолютно.
Вывод: ряд ![]() сходится абсолютно.
сходится абсолютно.
Правда, при втором способе решения есть риск, что преподаватель оценит хитро… смекалку студента и забракует задание. А может и не забракует. Ибо условие не предписывает использовать именно признак Лейбница (но обычно это всё же подразумевается).
И напоследок пара примеров для самостоятельного решения. Один из той же оперы (перечитайте справку), но попроще. Другой для гурманов – на закрепление интегрального признака сходимости.
Пример 9
Исследовать ряд на сходимость ![]()
Пример 10
Исследовать ряд на сходимость ![]()
После качественной проработки числовых положительных и знакопеременных рядов с чистой совестью можно перейти к функциональным рядам, которые не менее монотонны и однообразны интересны.
Желаю успехов!
Решения и ответы:
Пример 4: Используем признак Лейбница:
1) ![]() – данный ряд является знакочередующимся.
– данный ряд является знакочередующимся.
2)
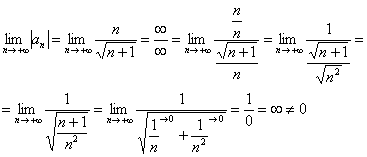
Члены ряда не убывают по модулю, следовательно, предела ![]() не существует, и ряд расходится, т.к. не выполнен необходимый признак сходимости.
не существует, и ряд расходится, т.к. не выполнен необходимый признак сходимости.
Вывод: ряд расходится.
Примечание: в данном примере неопределенность ![]() устраняется стандартным способом: делением числителя и знаменателя на «эн» в старшей степени. Старшая степень числителя: 1, старшая степень знаменателя:
устраняется стандартным способом: делением числителя и знаменателя на «эн» в старшей степени. Старшая степень числителя: 1, старшая степень знаменателя: ![]()
Пример 5: Используем признак Лейбница.
1) ![]() – ряд является знакочередующимся.
– ряд является знакочередующимся.
2) ![]() – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше предыдущего:
– члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше предыдущего: ![]() , т.е. убывание монотонно.
, т.е. убывание монотонно.
Таким образом, ряд сходится по признаку Лейбница.
С помощью ряда, составленного из модулей, выясним как именно:
![]()
Сравним данный ряд с расходящимся гармоническим рядом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
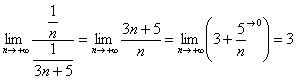 – конечное число, отличное от нуля, значит, ряд
– конечное число, отличное от нуля, значит, ряд ![]() расходится вместе с гармоническим рядом.
расходится вместе с гармоническим рядом.
Таким образом, ряд ![]() сходится условно.
сходится условно.
Пример 7: Используем признак Лейбница.
1) ![]() – ряд является знакочередующимся.
– ряд является знакочередующимся.
2) ![]() – члены ряда убывают по модулю. Найдём модуль
– члены ряда убывают по модулю. Найдём модуль ![]() -го члена:
-го члена: ![]() . Для любого номера
. Для любого номера ![]() справедливо неравенство :
справедливо неравенство :
![]() (
(![]() ), т.е. члены убывают монотонно.
), т.е. члены убывают монотонно.
Ряд сходится по признаку Лейбница.
Исследуем характер сходимости:
![]()
Используем признак Даламбера:
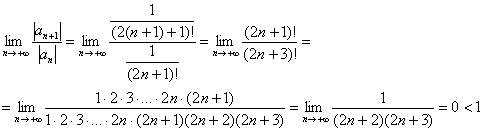
Таким образом, ряд![]() сходится.
сходится.
Ряд ![]() сходится абсолютно.
сходится абсолютно.
Примечание: Возможно, не всем понятно, как разложены факториалы. Это всегда можно установить опытным путём, возьмём и сравним какие-нибудь соседние члены ряда:
![]() и
и ![]() , следующий член ряда к предыдущему:
, следующий член ряда к предыдущему: 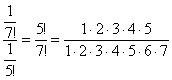
![]() и
и ![]() , следующий член ряда к предыдущему:
, следующий член ряда к предыдущему: 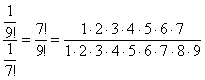
…
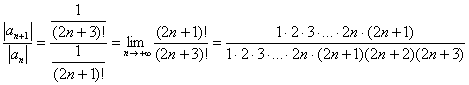
Пример 9: Используем признак Лейбница:
1) ![]()
Ряд является знакочередующимся.
2) ![]() – члены ряда монотонно убывают по модулю (так как
– члены ряда монотонно убывают по модулю (так как ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() ) .
) .
Таким образом, ряд сходится. Выясним, абсолютно или условно:
![]()
Используем признак Даламбера:
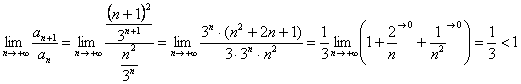 , следовательно , ряд
, следовательно , ряд ![]() сходится.
сходится.
Исследуемый ряд сходится абсолютно.
Пример 10: Используем признак Лейбница.
1) ![]()
Ряд является знакочередующимся.
2) ![]() – члены ряда убывают по модулю, и очевидно, что
– члены ряда убывают по модулю, и очевидно, что ![]() – каждый следующий член ряда по модулю меньше предыдущего:
– каждый следующий член ряда по модулю меньше предыдущего: ![]() , т.е. убывание монотонно.
, т.е. убывание монотонно.
Ряд сходится по признаку Лейбница.
Исследуем ряд, составленный из модулей:
![]()
Используем интегральный признак.
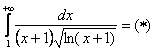
Подынтегральная функция непрерывна на ![]() .
.
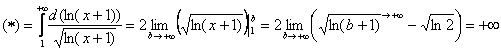
Таким образом, ряд ![]() расходится вместе с соответствующим несобственным интегралом.
расходится вместе с соответствующим несобственным интегралом.
Исследуемый ряд сходится условно.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
