
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Собственные значения (числа) и собственные векторы.
Примеры решений
Будь собой
Второй урок о линейных преобразованиях будет посвящён собственным числам и собственным значениям их матриц, и для более интересного чтения я рекомендую ознакомиться с первой статьёй. Однако если у вас совсем нет времени/сил/желания, то задачи этой страницы можно освоить и чисто формально. С небольшой художественной формальности я, собственно, и начну:
Рассмотрим произвольную квадратную матрицу, например, ![]() . И умножим данную матрицу справа на какой-нибудь подходящий столбец. Мне пришёл в голову вектор
. И умножим данную матрицу справа на какой-нибудь подходящий столбец. Мне пришёл в голову вектор ![]() :
:
![]()
Вроде ничего примечательного – умножили матрицу ![]() на вектор-столбец
на вектор-столбец ![]() и получили другой вектор-столбец
и получили другой вектор-столбец ![]() . Обычная векторная жизнь. Но в обществе таких векторов существуют особые представители, которые обладают внутренним стержнем и не желают изменять себе в трудные минуты.
. Обычная векторная жизнь. Но в обществе таких векторов существуют особые представители, которые обладают внутренним стержнем и не желают изменять себе в трудные минуты.
Умножим ту же матрицу на ![]() :
:
![]()
На последнем шаге вынесли константу. Что произошло? В результате умножения матрицы ![]() на вектор
на вектор ![]() , данный вектор птицей Феникс возродился с числовым коэффициентом
, данный вектор птицей Феникс возродился с числовым коэффициентом ![]() :
:
![]()
Определение: ненулевой вектор ![]() , который при умножении на некоторую квадратную матрицу
, который при умножении на некоторую квадратную матрицу ![]() превращается в самого же себя с числовым коэффициентом
превращается в самого же себя с числовым коэффициентом ![]() , называется собственным вектором матрицы
, называется собственным вектором матрицы ![]() . Число
. Число ![]() называют собственным значением или собственным числом данной матрицы.
называют собственным значением или собственным числом данной матрицы.
Поскольку каждой квадратной матрице соответствует определенное линейное преобразование (в некотором базисе), то, исходя из содержательного смысла, часто говорят о собственных значениях и собственных векторах линейного преобразования.
В Википедии есть удачный геометрический пример (взгляните!), иллюстрирующий рассматриваемые понятия – на репродукции Джоконды синий вектор не меняется в результате перекоса плоскости, а значит, является собственным вектором данного линейного преобразования с коэффициентом ![]() . И из комментария к иллюстрации можно сразу узнать, что любой коллинеарный ему вектор – тоже будет собственным вектором данного линейного преобразования. Я скуп на внешние ссылки, но здесь не удержался, пожалуйста, сообщите, если эту картинку вдруг удалят.
. И из комментария к иллюстрации можно сразу узнать, что любой коллинеарный ему вектор – тоже будет собственным вектором данного линейного преобразования. Я скуп на внешние ссылки, но здесь не удержался, пожалуйста, сообщите, если эту картинку вдруг удалят.
Примеры ещё будут, примеры интересные, ну а пока что продолжаем:
В первых абзацах статьи собственный вектор был выставлен «главным действующим лицом», но на самом деле всё немного не так: говорят, что собственный вектор ![]() соответствует собственному значению
соответствует собственному значению ![]() . И в практических заданиях сначала разыскиваются собственные числа и только потом соответствующие им собственные векторы.
. И в практических заданиях сначала разыскиваются собственные числа и только потом соответствующие им собственные векторы.
Как найти собственные значения и собственные векторы матрицы?
Проведём исследование и получим алгоритм, по которому нужно решать данную задачу. Люди, которые не очень хорошо разбираются в математике (да и которые хорошо) обычно в страхе или отвращении захлопывают учебник, когда речь заходит о каком-либо доказательстве или выводе какой-нибудь формулы. Но это не тот случай – всё будет понятно даже полному чайнику:
Пример 1
Найти собственные числа и собственные векторы матрицы
![]()
Перед вами та же матрица, у которой я уже выдал одно собственное значение и один собственный вектор. Давайте научимся добывать их самостоятельно!
Обозначим через ![]() неизвестный собственный вектор. Тогда матричное уравнение
неизвестный собственный вектор. Тогда матричное уравнение ![]() запишется следующим образом:
запишется следующим образом:
![]()
В левой части по обычному правилу проведём матричное умножение, в правой части – внесём «лямбду»:
![]()
Две матрицы равны, если равны их соответствующие элементы. Приравниваем соответствующие элементы векторов-столбцов и получаем однородную систему линейных уравнений:
![]()
Перенесём всё налево:
![]()
В первом уравнении за скобки вынесем «икс», во втором уравнении – «игрек»:
![]()
По определению, собственный вектор не может быть нулевым ![]() , поэтому нас не устраивает тривиальное решение
, поэтому нас не устраивает тривиальное решение ![]() системы. А если однородная система имеет ненулевое решение, то её уравнения линейно зависимы и определитель матрицы равен нулю:
системы. А если однородная система имеет ненулевое решение, то её уравнения линейно зависимы и определитель матрицы равен нулю:
![]()
Это так называемое характеристическое уравнение матрицы ![]() , корни которого являются собственными числами данной матрицы.
, корни которого являются собственными числами данной матрицы.
На практике, как правило, не нужно расписывать подробный вывод формулы – вполне достаточно руководствоваться формальным алгоритмом, и решение задачи можно начать примерно так:
Сначала найдём собственные значения
Составим характеристическое уравнение. Смотрим на исходную матрицу ![]() и записываем её определитель, вычитая при этом «лямбду» из чисел главной диагонали:
и записываем её определитель, вычитая при этом «лямбду» из чисел главной диагонали:
![]()
Раскроем определитель и решим квадратное уравнение:
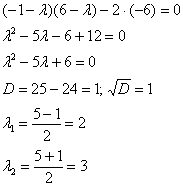
Таким образом, собственные значения: ![]()
Желательно располагать их в порядке возрастания, хотя это не принципиально.
Теперь найдём собственные векторы
В данном примере получены различные собственные числа и каждому из них соответствует свои собственные векторы.
1) Рассмотрим собственное число ![]() и подставим значение
и подставим значение ![]() в однородную систему уравнений
в однородную систему уравнений ![]() :
:
![]()
Для записи системы целесообразно запомнить формальный приём: мысленно либо на черновике подставляем ![]() в определитель
в определитель ![]() :
:
![]() – это и есть коэффициенты системы.
– это и есть коэффициенты системы.
Из обоих уравнений следует:
![]()
Если в ходе решения выяснилось, что линейной зависимости нет (т.е. получается только тривиальное решение, в данном примере ![]() ) – ищите ошибку! Этот признак касается всех задач рассматриваемого типа.
) – ищите ошибку! Этот признак касается всех задач рассматриваемого типа.
Итак, в нашем распоряжении есть выражение ![]() , и, придавая переменной «игрек» (либо «икс») произвольные значения, мы получаем бесконечно много собственных векторов
, и, придавая переменной «игрек» (либо «икс») произвольные значения, мы получаем бесконечно много собственных векторов ![]() . Все они будут коллинеарны друг другу, и поэтому нам достаточно указать один из них. Обычно стараются выбрать «красивый» вектор – чтобы его «иксовая» координата была положительной, целой и минимальной, а «игрек» не дробным.Этому эстетическому критерию соответствует значение
. Все они будут коллинеарны друг другу, и поэтому нам достаточно указать один из них. Обычно стараются выбрать «красивый» вектор – чтобы его «иксовая» координата была положительной, целой и минимальной, а «игрек» не дробным.Этому эстетическому критерию соответствует значение ![]() , тогда:
, тогда:
![]()
Теперь обязательно проверяем, что частное решение ![]() удовлетворяет каждому уравнению системы:
удовлетворяет каждому уравнению системы:
![]()
Таким образом: ![]() – первый собственный вектор.
– первый собственный вектор.
2) Найдём собственные векторы, соответствующие числу ![]() . Для этого мысленно либо на черновике подставим его в определитель
. Для этого мысленно либо на черновике подставим его в определитель ![]() и запишем вторую однородную систему:
и запишем вторую однородную систему:
![]()
Из обоих уравнений следует, что ![]() .
.
Положим ![]() , тогда:
, тогда: ![]() .
.
В результате: ![]() – второй собственный вектор.
– второй собственный вектор.
Повторим важные моменты решения:
– полученная система ![]() непременно имеет общее решение (уравнения линейно зависимы);
непременно имеет общее решение (уравнения линейно зависимы);
– «игрек» подбираем таким образом, чтобы он был целым и первая «иксовая» координата – целой, положительной и как можно меньше.
– проверяем, что частное решение ![]() удовлетворяет каждому уравнению системы.
удовлетворяет каждому уравнению системы.
Ответ: собственные числа: ![]() , собственные векторы:
, собственные векторы: ![]() .
.
Промежуточных «контрольных точек» было вполне достаточно, поэтому проверка равенств ![]() , в принципе, дело излишнее.
, в принципе, дело излишнее.
В различных источниках информации координаты собственных векторов довольно часто записывают не в столбцы, а в строки, например: ![]() (и, если честно, я сам привык записывать их строками). Такой вариант приемлем, но в свете темы линейных преобразований технически удобнее использовать векторы-столбцы.
(и, если честно, я сам привык записывать их строками). Такой вариант приемлем, но в свете темы линейных преобразований технически удобнее использовать векторы-столбцы.
Возможно, решение показалась вам очень длинным, но это только потому, что я очень подробно прокомментировал первый пример.
Пример 2
Найти собственные числа и собственные векторы матрицы
![]()
Тренируемся самостоятельно! Примерный образец чистового оформления задачи в конце урока.
Иногда требуется выполнить дополнительное задание, а именно:
записать каноническое разложение матрицы
Что это такое?
Если собственные векторы матрицы ![]() образуют базис, то она представима в виде:
образуют базис, то она представима в виде:
![]() , где
, где ![]() – матрица составленная из координат собственных векторов,
– матрица составленная из координат собственных векторов, ![]() – диагональная матрица с соответствующими собственными числами.
– диагональная матрица с соответствующими собственными числами.
Такое разложение матрицы называют каноническим или спектральным.
Рассмотрим матрицу ![]() первого примера. Её собственные векторы
первого примера. Её собственные векторы ![]() линейно независимы (неколлинеарны) и образуют базис. Составим матрицу из их координат:
линейно независимы (неколлинеарны) и образуют базис. Составим матрицу из их координат:
![]()
На главной диагонали матрицы ![]() в соответствующем порядке располагаются собственные числа, а остальные элементы равняются нулю:
в соответствующем порядке располагаются собственные числа, а остальные элементы равняются нулю:
![]() – ещё раз подчёркиваю важность порядка: «двойка» соответствует 1-му вектору и посему располагается в 1-м столбце, «тройка» – 2-му вектору.
– ещё раз подчёркиваю важность порядка: «двойка» соответствует 1-му вектору и посему располагается в 1-м столбце, «тройка» – 2-му вектору.
По обычному алгоритму нахождения обратной матрицы либо методом Гаусса-Жордана находим ![]() . Нет, это не опечатка! – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей.
. Нет, это не опечатка! – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей.
Осталось записать каноническое разложение матрицы ![]() :
:
![]()
Желающие могут перемножить три матрицы и удостовериться, что произведение равно ![]() .
.
Разрешив матричное уравнение ![]() относительно диагональной матрицы, можно получить другое соотношение:
относительно диагональной матрицы, можно получить другое соотношение:
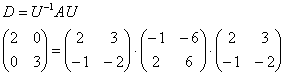
Диагональную матрицу ![]() также называют матрицей линейного преобразования в базисе из собственных векторов. Если не очень понятно, то давайте вспомним заключительную часть урока о линейных преобразованиях. В ней мы выяснили, что одному и тому же линейному преобразованию в разных базисах в общем случае соответствуют разные матрицы (в частности, матрицы
также называют матрицей линейного преобразования в базисе из собственных векторов. Если не очень понятно, то давайте вспомним заключительную часть урока о линейных преобразованиях. В ней мы выяснили, что одному и тому же линейному преобразованию в разных базисах в общем случае соответствуют разные матрицы (в частности, матрицы ![]() и
и ![]() в нашем примере). И наиболее удобным из них как раз и является базис из собственных векторов (в случае его существования).
в нашем примере). И наиболее удобным из них как раз и является базис из собственных векторов (в случае его существования).
Более того, все матрицы конкретного линейного преобразования в одном и том же векторном пространстве имеют один и то же характеристический многочлен, из-за чего характеристическое уравнение, вероятно, и получило своё название.
Так, легко убедиться, что характеристическое уравнение матрицы ![]() :
:
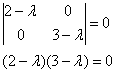
![]() – совпадает с характеристическим уравнением матрицы
– совпадает с характеристическим уравнением матрицы ![]() , которое мы получили в 1-м примере.
, которое мы получили в 1-м примере.
Однако такой удобный базис существует далеко не всегда:
Пример 3
Найти каноническое разложение матрицы
![]()
Решение: найдем собственные значения. Составим и решим характеристическое уравнение:
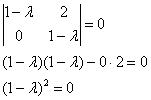
![]() – получены кратные собственные числа.
– получены кратные собственные числа.
Мысленно либо на черновике подставим ![]() в определитель
в определитель ![]() и запишем однородную систему линейных уравнений:
и запишем однородную систему линейных уравнений:
![]()
Очевидно, «игрек» равен нулю: ![]() (иначе в первом уравнении получится неверное равенство). За «икс» можно принять любое ненулевое значение, в хорошем стиле положим, что
(иначе в первом уравнении получится неверное равенство). За «икс» можно принять любое ненулевое значение, в хорошем стиле положим, что ![]() . Не ленимся и проверяем, что эта пара значений удовлетворяет каждому уравнению системы!
. Не ленимся и проверяем, что эта пара значений удовлетворяет каждому уравнению системы!
Таким образом, кратным собственным числам соответствует одно множество коллинеарных друг другу собственных векторов в «лице» вектора ![]() , и поэтому канонического разложения матрицы
, и поэтому канонического разложения матрицы ![]() не существует.
не существует.
Почему? Потому что невозможно записать матрицу ![]() , которая должна состоять из двух линейно независимых собственных векторов. Размерность вектора равна двум («икс» и «игрек»), но сам-то вектор – один-одинёшенек. Коллинеарный товарищ, например
, которая должна состоять из двух линейно независимых собственных векторов. Размерность вектора равна двум («икс» и «игрек»), но сам-то вектор – один-одинёшенек. Коллинеарный товарищ, например ![]() , в пару не годится (хотя бы по той причине, что
, в пару не годится (хотя бы по той причине, что ![]() и обратной матрицы
и обратной матрицы ![]() попросту не существует).
попросту не существует).
У рассмотренного примера есть простое геометрическое объяснение: матрица ![]() определяет не что иное, как «перекос Джоконды», у которого существует лишь одно множество коллинеарных друг другу собственных векторов, которые это линейное преобразование переводит в коллинеарные исходным, причём равные векторы (коль скоро,
определяет не что иное, как «перекос Джоконды», у которого существует лишь одно множество коллинеарных друг другу собственных векторов, которые это линейное преобразование переводит в коллинеарные исходным, причём равные векторы (коль скоро, ![]() )
)
Ответ: собственные векторы не образуют базиса, поэтому требуемое разложение неосуществимо.
Обратите внимание на корректность и точность ответа – нас никто не спрашивал о собственных значениях и собственных векторах. Кстати, об условии – его могут сформулировать и коварно: записать матрицу ![]() линейного преобразования в базисе из собственных векторов. Коварство состоит в том, что здесь можно найти собственные числа и машинально дать нелегальный ответ
линейного преобразования в базисе из собственных векторов. Коварство состоит в том, что здесь можно найти собственные числа и машинально дать нелегальный ответ ![]() . Но базиса-то не существует!
. Но базиса-то не существует!
И сейчас назрели важные вопросы:
Сколько у матрицы собственных чисел и собственных векторов?
Ну, во-первых (вроде не говорил), эти понятия определены только для квадратных матриц.
И с собственными числами всё просто:
у матрицы ![]() существует ровно
существует ровно ![]() собственных значений.
собственных значений.
Могут ли они быть комплексными? Запросто. Простейший пример: ![]() – матрица поворота декартовой системы координат
– матрица поворота декартовой системы координат ![]() против часовой стрелки на угол
против часовой стрелки на угол ![]() , отличный от 180 и 360 градусов. Возьмём «школьный» угол в 30 градусов, запишем соответствующую матрицу поворота
, отличный от 180 и 360 градусов. Возьмём «школьный» угол в 30 градусов, запишем соответствующую матрицу поворота 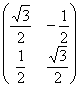 и составим характеристическое уравнение:
и составим характеристическое уравнение:
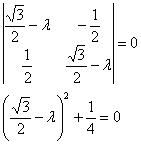
Оно имеет сопряжённые комплексные корни ![]() , и дальнейшее решение показывает, что у рассматриваемого преобразования нет действительных собственных векторов. И это очевидно – при повороте на 30 градусов любой ненулевой вектор отображается в неколлинеарный ему вектор.
, и дальнейшее решение показывает, что у рассматриваемого преобразования нет действительных собственных векторов. И это очевидно – при повороте на 30 градусов любой ненулевой вектор отображается в неколлинеарный ему вектор.
Случай второй, самый распространённый. Собственные числа матрицы ![]() действительны и различны (как, например, в Примерах 1, 2). Такое линейное преобразование имеет ровно
действительны и различны (как, например, в Примерах 1, 2). Такое линейное преобразование имеет ровно ![]() собственных линейно независимых векторов, и его недиагональную матрицу всегда можно записать в виде
собственных линейно независимых векторов, и его недиагональную матрицу всегда можно записать в виде ![]() .
.
Случай третий, самый интересный. Среди собственных чисел есть кратные, или же только кратные, как в Примере 3. В этих случаях неколлинеарных собственных векторов может оказаться… сколько угодно! Меньше, чем собственных чисел (Пример 3). Может оказаться ровно ![]() штук, и тогда будет существовать разложение
штук, и тогда будет существовать разложение ![]() .
.
А может – вообще бесконечно много! Например, при повороте плоскости на 180 градусов. Ему соответствует матрица ![]() с характеристическим уравнением
с характеристическим уравнением ![]() с кратными собственными числами
с кратными собственными числами ![]() ; и, продолжая стандартное решение, мы приходим к симпатичной системе
; и, продолжая стандартное решение, мы приходим к симпатичной системе ![]() , которой удовлетворяют координаты вообще любого вектора. Таким образом, любой ненулевой вектор этого преобразования является собственным! Оно и неудивительно – ведь при повороте на 180 градусов любой ненулевой вектор отображается в коллинеарный и противоположно направленный вектор, например:
, которой удовлетворяют координаты вообще любого вектора. Таким образом, любой ненулевой вектор этого преобразования является собственным! Оно и неудивительно – ведь при повороте на 180 градусов любой ненулевой вектор отображается в коллинеарный и противоположно направленный вектор, например:
![]() , и, вынося собственное число из столбца:
, и, вынося собственное число из столбца: ![]() , мы окончательно убеждаемся, что
, мы окончательно убеждаемся, что ![]() – есть собственный вектор.
– есть собственный вектор.
Следует отметить, что этот поворот – частный случай преобразования подобия, и у подобия, к слову, тоже любой ненулевой вектор собственный. Коэффициент же подобия – есть не что иное, как соответствующее собственное значение, в частности, при ![]() все геометрические объекты сохраняют свои размеры неизменными
все геометрические объекты сохраняют свои размеры неизменными
Однако не будем слишком увлекаться геометрией – ведь в термины вектор, базис и др. вкладывается, прежде всего, алгебраический смысл. Собственные векторы и собственные значения используются во многих математических задачах, моделях, но мы не будем увлекаться и ими :) – сейчас важно освоить техническую сторону вопроса.
И задачи с матрицей «три на три» отличаются бОльшей технической сложностью:
Пример 4
Найти собственные векторы линейного преобразования, заданного матрицей
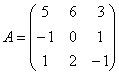
Решение: такая формулировка задачи смущать не должна – ведь это и есть «генеральная линия партии». Энтузиасты могут провести самостоятельные выкладки по аналогии с Примером № 1, я же ограничусь «рабочим» решением примера.
По условию требуется найти собственные векторы, но алгоритм таков, что в первую очередь всё равно нужно найти собственные числа.
Вычтем «лямбду» из всех чисел главной диагонали матрицы ![]() и составим её характеристическое уравнение:
и составим её характеристическое уравнение:
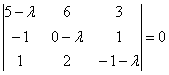
Определитель раскроем по первому столбцу:
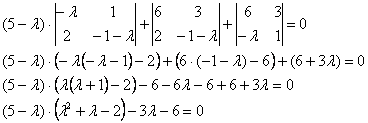
На этом месте немного притормозим и познакомимся с очень полезным техническим приёмом, который значительно упростит дальнейшую жизнь. Практически во всех методических пособиях вам будет предложено раскрыть все скобки, получить слева многочлен 3-й степени, затем подбором найти корень и стать жертвой долгих мытарств, описанных в Примере № 1 урока Сложные пределы. За годы практики я отработал рациональную схему, позволяющую избежать этих неприятностей:
Сначала представим в виде произведения «хвост» левой части:
![]()
Выполненное действие не привело к заметному результату.
Поэтому пробуем разложить на множители квадратный трёхчлен ![]() . Решив квадратное уравнение, получаем
. Решив квадратное уравнение, получаем ![]() .
.
Таким образом:
![]()
Вынесем ![]() за скобку и проведём дальнейшие упрощения:
за скобку и проведём дальнейшие упрощения:
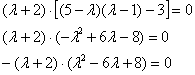
Решаем ещё одно квадратное уравнение, в итоге:
![]()
Это была самая длинная ветка алгоритма, в большинстве случаев произведение получается значительно быстрее.
Собственные значения всегда стараемся расположить в порядке возрастания:
![]()
Найдем собственные векторы:
1) Мысленно либо на черновике подставим значение ![]() в определитель
в определитель 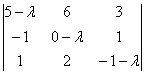 , с которого «снимем» коэффициенты однородной системы:
, с которого «снимем» коэффициенты однородной системы:
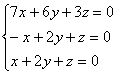
Систему можно решить с помощью элементарных преобразований и в следующих примерах мы прибегнем к данному методу. Но здесь гораздо быстрее срабатывает «школьный» способ. Из 3-го уравнения выразим: ![]() – подставим во второе уравнение:
– подставим во второе уравнение:
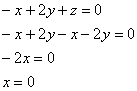
Поскольку первая координата нулевая, то получаем систему 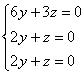 , из каждого уравнения которой следует, что
, из каждого уравнения которой следует, что ![]() .
.
И снова обратите внимание на обязательное наличие линейной зависимости. Если получается только тривиальное решение ![]() , то либо неверно найдено собственное число, либо с ошибкой составлена / решена система.
, то либо неверно найдено собственное число, либо с ошибкой составлена / решена система.
Компактные координаты даёт значение ![]()
Собственный вектор: 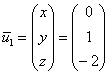
И ещё раз – проверяем, что найденное решение ![]() удовлетворяет каждому уравнению системы. В последующих пунктах и в последующих задачах рекомендую принять данное пожелание за обязательное правило.
удовлетворяет каждому уравнению системы. В последующих пунктах и в последующих задачах рекомендую принять данное пожелание за обязательное правило.
2) Для собственного значения ![]() по такому же принципу получаем следующую систему:
по такому же принципу получаем следующую систему:
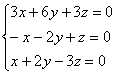
Из 2-го уравнения системы выразим: ![]() – подставим в третье уравнение:
– подставим в третье уравнение:
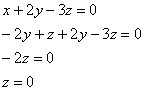
Поскольку «зетовая» координата равна нулю, то получаем систему 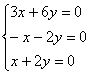 , из каждого уравнения которой следует линейная зависимость
, из каждого уравнения которой следует линейная зависимость ![]() .
.
Пусть ![]()
Проверяем, что решение ![]() удовлетворяет каждому уравнению системы.
удовлетворяет каждому уравнению системы.
Таким образом, собственный вектор: 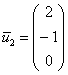 .
.
3) И, наконец, собственному значению ![]() соответствует система:
соответствует система:
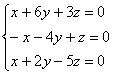
Второе уравнение выглядит самым простым, поэтому из него выразим ![]() и подставим в 1-е и 3-е уравнение:
и подставим в 1-е и 3-е уравнение:
![]()
Всё хорошо – выявилась линейная зависимость ![]() , которую подставляем в выражение
, которую подставляем в выражение ![]() :
:
![]()
В результате «икс» и «игрек» оказались выражены через «зет»: ![]() . На практике не обязательно добиваться именно таких взаимосвязей, в некоторых случаях удобнее выразить
. На практике не обязательно добиваться именно таких взаимосвязей, в некоторых случаях удобнее выразить ![]() и
и ![]() через
через ![]() либо
либо ![]() и
и ![]() через
через ![]() . Или даже «паровозиком» – например, «икс» через «игрек», а «игрек» через «зет»
. Или даже «паровозиком» – например, «икс» через «игрек», а «игрек» через «зет»
Положим ![]() , тогда:
, тогда:
![]()
Проверяем, что найденное решение ![]() удовлетворяет каждому уравнению системы и записываем третий собственный вектор
удовлетворяет каждому уравнению системы и записываем третий собственный вектор 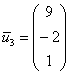
Ответ: собственные векторы: 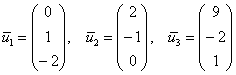
Геометрически эти векторы задают три различных пространственных направления («туда-обратно»), по которым линейное преобразование переводит ненулевые векторы (собственные векторы) в коллинеарные им векторы.
Если бы по условию требовалось найти каноническое разложение ![]() , то здесь это возможно, т. к. различным собственным числам соответствуют разные линейно независимые собственные векторы. Составляем матрицу
, то здесь это возможно, т. к. различным собственным числам соответствуют разные линейно независимые собственные векторы. Составляем матрицу 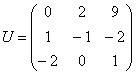 из их координат, диагональную матрицу
из их координат, диагональную матрицу 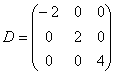 из соответствующих собственных значений и находим обратную матрицу
из соответствующих собственных значений и находим обратную матрицу ![]() .
.
Если же по условию нужно записать матрицу линейного преобразования в базисе из собственных векторов, то просто указываем матрицу ![]() . Внимательно читайте, что требует условие той или иной задачи!
. Внимательно читайте, что требует условие той или иной задачи!
Задача с более простыми вычислениями для самостоятельного решения:
Пример 5
Найти собственные векторы линейного преобразования, заданного матрицей
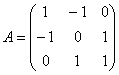
При нахождении собственных чисел постарайтесь не доводить дело до многочлена 3-й степени. Системы можно решать разными путями – здесь нет однозначности, а векторы, которые вы укажите, могут отличаться от векторов в образце с точностью до пропорциональности их соответствующих координат. Например, 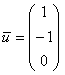 и
и 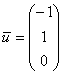 . Эстетичнее представить ответ в виде
. Эстетичнее представить ответ в виде 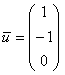 , но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, версия
, но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, версия 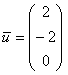 смотрится уже не очень хорошо.
смотрится уже не очень хорошо.
Примерный чистовой образец оформления задания в конце урока.
Как решать задачу в случае кратных собственных чисел?
Общий алгоритм остаётся прежним, но здесь есть свои особенности, и некоторые участки решения целесообразно выдержать в более строгом академичном стиле:
Пример 6
Найти собственные числа и собственные векторы
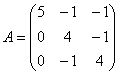
Решение: составим и решим характеристическое уравнение:
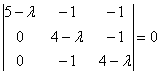
Конечно же, оприходуем сказочный первый столбец:
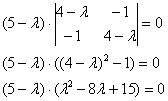
И, после разложения квадратного трёхчлена на множители:
![]()
В результате получены собственные числа ![]() , два из которых кратны.
, два из которых кратны.
Найдем собственные векторы:
1) С одиноким солдатом ![]() разделаемся по «упрощённой» схеме:
разделаемся по «упрощённой» схеме:
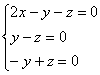
Из последних двух уравнений четко просматривается равенство ![]() , которое, очевидно, следует подставить в 1-е уравнение системы:
, которое, очевидно, следует подставить в 1-е уравнение системы:
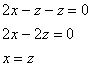
Лучшей комбинации не найти: ![]()
Собственный вектор: 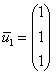
2-3) Теперь снимаем пару часовых. В данном случае может получиться либо два, либо один собственный вектор. Невзирая на кратность корней, подставим значение ![]() в определитель
в определитель 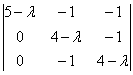 , который приносит нам следующую однородную систему линейных уравнений:
, который приносит нам следующую однородную систему линейных уравнений:
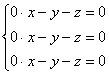
Собственные векторы – это в точности векторы
фундаментальной системы решений
Собственно, на протяжении всего урока мы только и занимались тем, что находили векторы фундаментальной системы. Просто до поры до времени данный термин особо не требовался. Кстати, те ловкие студенты, которые в маскхалатах проскочили тему однородных уравнений, будут вынуждены вкурить её сейчас.
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
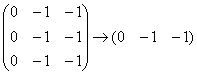
Единственное действие состояло в удалении лишних строк. В результате получена матрица «один на три» с формальной «ступенькой» посередине.
![]() – базисная переменная,
– базисная переменная, ![]() – свободные переменные. Свободных переменных две, следовательно, векторов фундаментальной системы тоже два.
– свободные переменные. Свободных переменных две, следовательно, векторов фундаментальной системы тоже два.
Выразим базисную переменную через свободные переменные: ![]() . Нулевой множитель перед «иксом» позволяет принимать ему совершенно любые значения (что хорошо видно и из системы уравнений).
. Нулевой множитель перед «иксом» позволяет принимать ему совершенно любые значения (что хорошо видно и из системы уравнений).
В контексте данной задачи общее решение удобнее записать не в строку, а в столбец:
![]()
Паре ![]() соответствует собственный вектор:
соответствует собственный вектор: 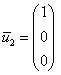
Паре ![]() соответствует собственный вектор:
соответствует собственный вектор: 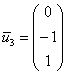
Примечание: искушенные читатели могут подобрать данные векторы и устно – просто анализируя систему 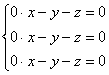 , но тут нужны некоторые знания: переменных – три, ранг матрицы системы – единица, значит, фундаментальная система решений состоит из 3 – 1 = 2 векторов. Впрочем, найденные векторы отлично просматриваются и без этих знаний чисто на интуитивном уровне. При этом даже «красивее» запишется третий вектор:
, но тут нужны некоторые знания: переменных – три, ранг матрицы системы – единица, значит, фундаментальная система решений состоит из 3 – 1 = 2 векторов. Впрочем, найденные векторы отлично просматриваются и без этих знаний чисто на интуитивном уровне. При этом даже «красивее» запишется третий вектор: 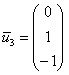 . Однако предостерегаю, в другом примере простого подбора может и не оказаться, именно поэтому оговорка предназначена для опытных людей. Кроме того, а почему бы не взять в качестве третьего вектора, скажем,
. Однако предостерегаю, в другом примере простого подбора может и не оказаться, именно поэтому оговорка предназначена для опытных людей. Кроме того, а почему бы не взять в качестве третьего вектора, скажем, 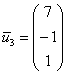 ? Ведь его координаты тоже удовлетворяют каждому уравнение системы, и векторы
? Ведь его координаты тоже удовлетворяют каждому уравнение системы, и векторы 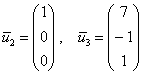 линейно независимы. Такой вариант, в принципе, годен, но «кривоват», поскольку «другой» вектор
линейно независимы. Такой вариант, в принципе, годен, но «кривоват», поскольку «другой» вектор 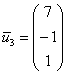 представляет собой линейную комбинацию
представляет собой линейную комбинацию 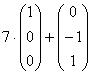 векторов фундаментальной системы.
векторов фундаментальной системы.
Ответ: собственные числа: ![]() , собственные векторы:
, собственные векторы: 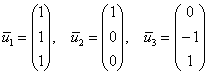
Аналогичный пример для самостоятельного решения:
Пример 7
Найти собственные числа и собственные векторы
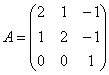
Примерный образец чистового оформления в конце урока.
Следует отметить, что и в 6-м и в 7-м примере получается тройка линейно независимых собственных векторов, и поэтому исходная матрица представима в каноническом разложении ![]() . Но такая малина бывает далеко не во всех случаях:
. Но такая малина бывает далеко не во всех случаях:
Пример 8
Найти собственные числа и собственные векторы матрицы
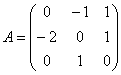
Решение: составим и решим характеристическое уравнение:
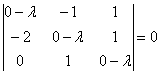
Определитель раскроем по первому столбцу:
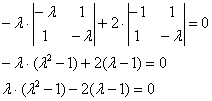
Дальнейшие упрощения проводим согласно рассмотренной методике, избегая многочлена 3-й степени:
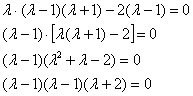
![]() – собственные значения.
– собственные значения.
Найдем собственные векторы:
1) С корнем ![]() затруднений не возникает:
затруднений не возникает:
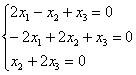
Не удивляйтесь, помимо комплекта ![]() в ходу также переменные
в ходу также переменные ![]() – разницы тут никакой.
– разницы тут никакой.
Из 3-го уравнения выразим ![]() – подставим в 1-е и 2-е уравнения:
– подставим в 1-е и 2-е уравнения:
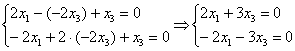
Из обоих уравнений следует: ![]()
Пусть ![]() , тогда:
, тогда:
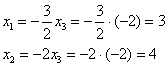
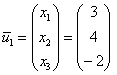
2-3) Для кратных значений ![]() получаем систему
получаем систему 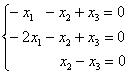 .
.
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
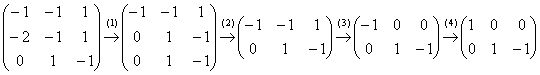
(1) Ко второй строке прибавили первую строку, умноженную на –2.
(2) Последние две строки одинаковы, одну из них удалили.
(3) Дальше пошла уместная доводка матрицы методом Гаусса-Жордана: к первой строке прибавили вторую строку.
(4) У первой строки сменили знак.
Переменные ![]() – базисные, переменная
– базисные, переменная ![]() – свободная. Так как свободная переменная одна, то фундаментальная система решений состоит из одного вектора. И мы счастливые наблюдатели случая, когда кратным собственным числам соответствует единственный собственный вектор. Записываем в столбец общее решение системы:
– свободная. Так как свободная переменная одна, то фундаментальная система решений состоит из одного вектора. И мы счастливые наблюдатели случая, когда кратным собственным числам соответствует единственный собственный вектор. Записываем в столбец общее решение системы: ![]() , и, задавая свободной переменной значение
, и, задавая свободной переменной значение ![]() , получаем нашего героя:
, получаем нашего героя:
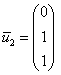
Ответ: собственные числа: ![]() , собственные векторы:
, собственные векторы: 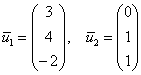 .
.
Здесь матрицу нельзя представить виде ![]() – по той простой причине, что «собственного» базиса не существует – хоть трёхмерные векторы-столбцы и линейно независимы, но самих-то их всего лишь два. Недобор.
– по той простой причине, что «собственного» базиса не существует – хоть трёхмерные векторы-столбцы и линейно независимы, но самих-то их всего лишь два. Недобор.
Шестое чувство мне подсказывает, что многие воодушевились на задание повышенной сложности:
Пример 9
Найти собственные числа и собственные векторы матрицы
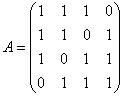
Можно ли записать каноническое разложение этой матрицы?
Не беда, если дело застопорилось, в психотерапевтических целях отложите тетрадь с решением на чёрный день. Когда заест скука – самое то =)
Успехов!
Решения и ответы:
Пример 2: Решение: Найдем собственные значения. Составим и решим характеристическое уравнение:
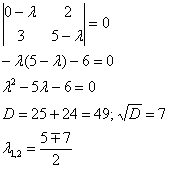
![]() – собственные значения.
– собственные значения.
Найдем собственные векторы:
1) ![]()
![]()
Пусть ![]()
![]() – собственный вектор.
– собственный вектор.
2) ![]()
![]()
Пусть ![]()
![]() – собственный вектор.
– собственный вектор.
Ответ: собственные значения: ![]() , собственные векторы:
, собственные векторы: ![]() .
.
Пример 5: Решение: сначала найдем собственные числа. Составим и решим характеристическое уравнение:
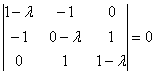
Определитель раскроем по первой строке:

![]() – собственные значения.
– собственные значения.
Найдем собственные векторы:
1) ![]()
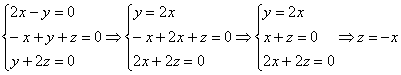
Пусть ![]()
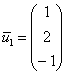
2) ![]()
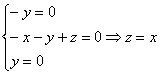
Пусть ![]()
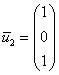
3) ![]()
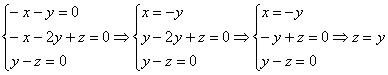
Пусть ![]()
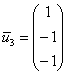
Ответ: собственные векторы: 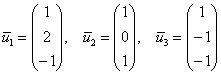
Пример 7: Решение: составим и решим характеристическое уравнение:

![]() – собственные значения.
– собственные значения.
Найдем собственные векторы:
1-2) ![]()
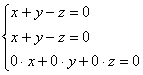
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
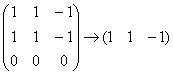
Выразим базисную переменную ![]() через свободные переменные:
через свободные переменные: ![]() и запишем общее решение:
и запишем общее решение: 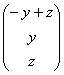 . Найдём векторы фундаментальной системы, которые и являются собственными векторами матрицы:
. Найдём векторы фундаментальной системы, которые и являются собственными векторами матрицы:
Паре ![]() соответствует собственный вектор:
соответствует собственный вектор: 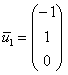
Паре ![]() соответствует собственный вектор:
соответствует собственный вектор: 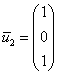
Примечание: в качестве решения системы линейных уравнений напрашивается тройка ![]() , но вектор
, но вектор ![]() линейно выражается через векторы фундаментальной системы. Использование такого и подобных ему решений в качестве одного из собственных векторов корректно, но нестандартно.
линейно выражается через векторы фундаментальной системы. Использование такого и подобных ему решений в качестве одного из собственных векторов корректно, но нестандартно.
3) ![]()
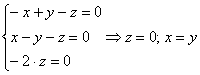
Пусть ![]()
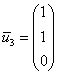
Ответ: собственные числа: ![]() , собственные векторы:
, собственные векторы:
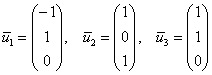
Пример 9: Решение: Составим и решим характеристическое уравнение:
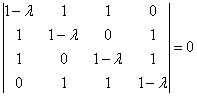
Определитель вычислим понижением порядка. К третьей строке прибавим вторую строку, умноженную на –1. К четвёртой строке прибавим вторую строку, умноженную на ![]() :
:
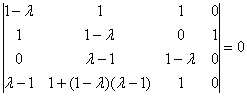
Разложим определитель по 4-му столбцу:
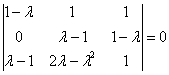
К третьей строке прибавим первую строку:
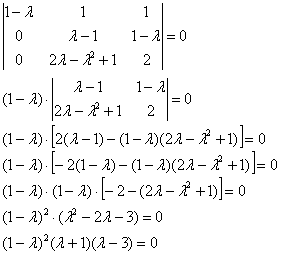
![]()
Собственные значения: ![]()
Найдем собственные векторы:
1) ![]()
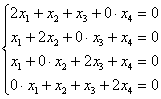
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
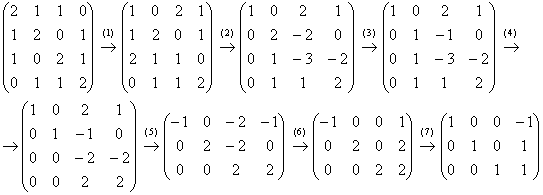
(1) Первую и третью строку поменяли местами.
(2) Ко 2-й и 3-й строкам прибавили первую строку, умноженную на –1 и –2 соответственно.
(3) Вторую строку разделили на 2.
(4) К 3-й и 4-й строкам прибавили вторую строку, умноженную на –1.
(5) Последние две строки пропорциональны, третью строку удалили. У первой строки сменили знак, вторую строку умножили на 2.
(6) К первой и второй строкам прибавили третью строку.
(7) У первой строки сменили знак, последние две строки разделили на 2.
Выразив базисные переменные через свободную, запишем общее решение: ![]() . Придаём свободной переменной значение
. Придаём свободной переменной значение ![]() и получаем собственный вектор
и получаем собственный вектор 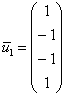
2-3) ![]()
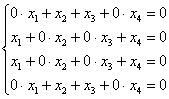
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
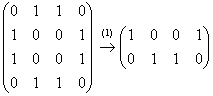
(1) Первая и четвёртая строки одинаковы. Вторая и третья строки одинаковы. Первую и вторую строку удалили из матрицы.
Выразим базисные переменные ![]() через свободные переменные
через свободные переменные ![]() :
:
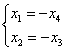
Таким образом, общее решение: ![]() .
.
Фундаментальная система состоит из двух векторов:
при ![]() получаем
получаем 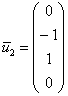 ;
;
при ![]() получаем
получаем 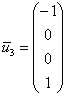 .
.
4) ![]()
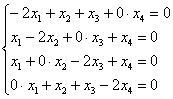
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
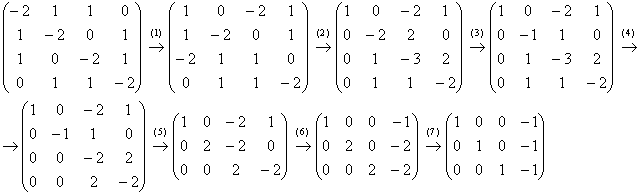
(1) Первую и третью строку поменяли местами.
(2) Ко 2-й и 3-й строкам прибавили первую строку, умноженную на –1 и 2 соответственно.
(3) Вторую строку разделили на 2.
(4) К 3-й и 4-й строкам прибавили вторую строку.
(5) Последние две строки пропорциональны, третью строку удалили. Вторую строку умножили на –2.
(6) К первой и второй строкам прибавили третью строку.
(7) Последние две строки разделили на 2.
Общее решение: ![]() . Придаём свободной переменной значение
. Придаём свободной переменной значение ![]() и получаем собственный вектор
и получаем собственный вектор 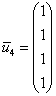 .
.
Ответ: собственные значения: ![]() , собственные векторы:
, собственные векторы:
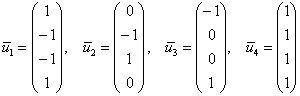 . Перечисленные четыре четырехмерных вектора линейно независимы, и поэтому матрицу линейного преобразования можно записать в виде
. Перечисленные четыре четырехмерных вектора линейно независимы, и поэтому матрицу линейного преобразования можно записать в виде ![]() . Но не нужно =)
. Но не нужно =)
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
