
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Экстремальные задачи с производной
Совершенно верно, иногда от таких задач действительно захватывает дух. Сегодня на уроке мы разберём ещё одно важное приложение производной, имеющее самое что ни на есть прикладное значение! Речь пойдёт о задачах с конкретным геометрическим, физическим, экономическим и т.д. содержанием, в которых исходя из условия, нужно самостоятельно составить функцию и найти её точку минимума либо максимума (и/или, соответственно, минимум либо максимум).
Для полноценного изучения урока необходимо уметь находить производные, ПОНИМАТЬ, что такое производная и быть знакомым с понятиями возрастания, убывания и экстремума функции. Таким образом, начинающим рекомендую начать с вышеуказанных статей, чтобы не словить здесь реальный экстрим =) А уже заматеревшие студенты не должны испытать особых трудностей. Разминочная алгебраическая задача и новый материал по ходу решения:
Задача 1
Известно, что сумма двух положительных чисел равна 12. Какими должны быть эти числа, чтобы произведение их квадратов было максимальным?
Решение: прежде всего, хорошо осознаем, что от нас требуется: в условии фигурируют два положительных числа, причём ни то, ни другое мы не знаем. Но вот их сумма равна 12.
Если это, например, 2 и 10, то произведение квадратов ![]() ;
;
если 7 и 5, то ![]() и т.д.
и т.д.
И нам нужно отыскать такую пару, для которой данное произведение будет наибольшим. Понятно, что с методом подбора тут замучаешься, к тому же искомые числа ведь могут оказаться и дробными. Поэтому привлечём на помощь могучий аппарат математического анализа.
Но сначала вспомним школу и вспомним, как, наивно хлопая ресницами, мы что-то обозначали за «икс»…. Обозначим за ![]() одно из чисел. Тогда второе число будет равно:
одно из чисел. Тогда второе число будет равно: ![]()
Проверим, что их сумма действительно равна 12:
![]() – а ведь и правду говорят, что всё гениальное просто =)
– а ведь и правду говорят, что всё гениальное просто =)
Теперь составим функцию произведения их квадратов:
![]()
Многие читатели уже понимают последующие шаги: далее нужно найти производную, критические точки и обнаружить точку (и), в которой функция ![]() достигает максимума (если таковые, конечно, вообще существуют).
достигает максимума (если таковые, конечно, вообще существуют).
И небольшой вопрос техники: производную здесь можно найти несколькими способами. На мой взгляд, удобен следующий вариант: загоняем множители под единую степень и раскрываем там скобки: ![]() , после чего дифференцируем сложную функцию:
, после чего дифференцируем сложную функцию:
![]()
Итак, ![]() – критические точки.
– критические точки.
По условию оба числа положительны, поэтому значения ![]() сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки
сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки ![]() и выяснить, достигает ли там функция
и выяснить, достигает ли там функция ![]() минимума либо максимума. А может статься, и ничего не достигает.
минимума либо максимума. А может статься, и ничего не достигает.
Проверка вам хорошо знакома: чертим числовую ось, выясняем знаки производной слева и справа от точки ![]() и выносим вердикт. Так решать можно, и это будет правильным решением, но есть и другой путь!
и выносим вердикт. Так решать можно, и это будет правильным решением, но есть и другой путь!
Второе достаточное условие экстремума
Пусть производная функции ![]() равна нулю в критической точке
равна нулю в критической точке ![]() :
:
![]() и пусть там существует вторая ненулевая производная:
и пусть там существует вторая ненулевая производная: ![]() . Тогда:
. Тогда:
если ![]() , то функция
, то функция ![]() достигает минимума в точке
достигает минимума в точке ![]() ;
;
если ![]() , то – максимума.
, то – максимума.
В нашем случае нужно найти вторую производную и вычислить ![]() – если окажется, что
– если окажется, что ![]() , то
, то ![]() является точкой минимума; если же
является точкой минимума; если же ![]() – то точкой максимума.
– то точкой максимума.
Для удобства дифференцирования утрамбуем предшественницу:
![]() и незамедлительно оценим это удобство:
и незамедлительно оценим это удобство:
![]()
Подставим критическое значение ![]() :
:
![]() , значит, функция
, значит, функция ![]() достигает максимума в данной точке:
достигает максимума в данной точке: ![]()
Ответ: искомые числа: 6 и 6, при этом максимальное произведение квадратов:
![]()
Вообще говоря, по условию не требовалось находить само произведение, но по правилам хорошо тона его лучше рассчитать и указать в ответе. К тому же это весьма любопытно.
На практике в подавляющем большинстве случаев встречаются задачи с геометрическим смыслом, и поэтому основная часть урока будет посвящена именно им. Начнём с несложного типового примера, который почему-то довольно часто вызывает проблемы:
Задача 2
Найти наименьшее расстояние между параболой ![]() и прямой
и прямой ![]()
Решение: вот, пожалуйста, самый что ни на есть практический смысл – представьте, что вам нужно пройти от дороги к дороге. Совершенно понятно, что в отсутствии препятствий это наиболее выгодно осуществить по кратчайшему пути.
Поскольку условие запрашивает наименьшее расстояние, то, очевидно, нам нужно составить функцию ![]() расстояния между параболой
расстояния между параболой ![]() и прямой
и прямой ![]() . За аргумент этой функции принимаем абсциссу точки
. За аргумент этой функции принимаем абсциссу точки ![]() , которая принадлежит параболе и «свободно перемещается по ней»:
, которая принадлежит параболе и «свободно перемещается по ней»:
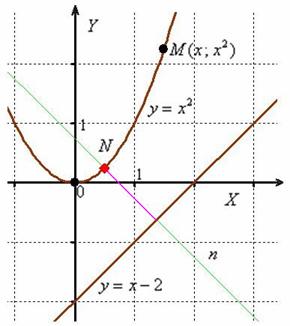
Используем формулу расстояния от точки ![]() до прямой
до прямой ![]() :
:
![]()
В нашем случае ![]() (т.е.
(т.е. ![]() );
);
![]() .
.
Таким образом:
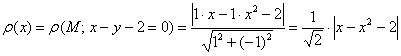 – функция расстояния между параболой и прямой, зависящая от абсциссы точки параболы.
– функция расстояния между параболой и прямой, зависящая от абсциссы точки параболы.
Дифференцируем по обычным правилам, невзирая на модуль:
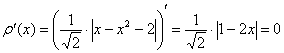
![]() – критическая точка
– критическая точка
Проверим выполнение достаточного условия экстремума. Оцените, насколько второе достаточное условие приятнее и удобнее 1-го:
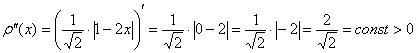 для всех «икс». В частности:
для всех «икс». В частности:
![]() , следовательно, функция
, следовательно, функция ![]() достигает минимума в точке
достигает минимума в точке ![]() :
:
![]()
Искомая «дорога» изображена малиновым отрезком на чертеже.
Ответ: ![]()
Физики в лирике могут найти ординату точки ![]() , уравнение нормали
, уравнение нормали ![]() и её точку пересечения с прямой
и её точку пересечения с прямой ![]() . Кстати, почему кратчайший путь проходит именно по нормали? Приложите ребро ладони к прямой
. Кстати, почему кратчайший путь проходит именно по нормали? Приложите ребро ладони к прямой ![]() и начните плавно сдвигать его к параболе: первая точка, которой вы коснётесь – будет в точности точка
и начните плавно сдвигать его к параболе: первая точка, которой вы коснётесь – будет в точности точка ![]() , ваша рука займёт положение касательной к графику функции
, ваша рука займёт положение касательной к графику функции ![]() в данной точке, а расстояние между двумя прямыми как раз и определится малиновым отрезком нормальной прямой.
в данной точке, а расстояние между двумя прямыми как раз и определится малиновым отрезком нормальной прямой.
Следующая задача для самостоятельного решения:
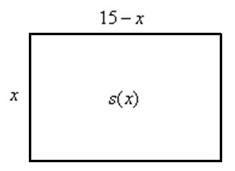
Задача 3
Из куска проволоки длиной 30 см требуется согнуть прямоугольник наибольшей площади. Каковы размеры этого прямоугольника?
Давайте немного проанализируем условие:
Что требуется найти? Очевидно, длину и ширину – это «традиционные» характеристики, определяющие прямоугольник.
Какую функцию нужно составить? Наверное, многие уже поняли данную закономерность:
Требуется найти минимальную/максимальную площадь? Составляем функцию площади;
Минимальную/максимальную диагональ? Составляем функцию длины диагонали;
Минимальный/максимальный периметр? Составляем функцию периметра
и т.д.
Напоминаю, что периметр – это длина границы фигуры, в данном случае – сумма длин сторон прямоугольника. Кстати, задачу легко переформулировать «чисто математически»:
«Найти прямоугольник максимальной площади, если его периметр равен 30 см»
Выполните схематический чертёж, подумайте, что обозначить за «икс» (впрочем, чего тут думать), составьте функцию площади ![]() – и дальше по накатанной.
– и дальше по накатанной.
Краткое решение и ответ в конце урока.
После простых разогревающих заданий рассмотрим что-нибудь поосновательнее:
Задача 4
На странице книги печатный текст должен занимать (вместе с промежутками между строк) 192 ![]() . Верхнее и нижнее поля занимают по 4 см, левое и правое – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
. Верхнее и нижнее поля занимают по 4 см, левое и правое – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
Решение: разруливаем задачу по той же логической схеме:
Что требуется найти? Наиболее выгодные размеры страницы. А страница обычно имеет форму прямоугольника. Коль скоро речь идёт об экономии бумаги, то, очевидно, нужно найти такую ширину и высоту листа, чтобы его площадь была минимальна. Из чего следует, что нам необходимо составить функцию площади страницы. Причём условие жёстко задаёт размеры полей, а вот под область печати отведено 192 ![]() и её размеры могут быть произвольными (заштрихованный прямоугольник на схематическом чертеже):
и её размеры могут быть произвольными (заштрихованный прямоугольник на схематическом чертеже):
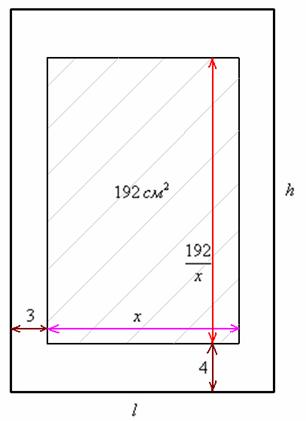
Обозначим за ![]() ширину области печати (малиновый отрезок) (можно обозначить высоту – получится равноценное решение). Тогда высота области печати:
ширину области печати (малиновый отрезок) (можно обозначить высоту – получится равноценное решение). Тогда высота области печати:
![]() (красный отрезок).
(красный отрезок).
Учитывая известные значения полей, найдём ширину всего листа:
![]()
И его высоту: ![]()
Составим функцию площади листа и сразу подготовим её для дифференцирования:
![]()
Найдём критические точки:
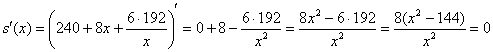
Точка ![]() не удовлетворяет геометрическому смыслу задачи, а вот значение
не удовлетворяет геометрическому смыслу задачи, а вот значение ![]() куда более интересно.
куда более интересно.
Проверим выполнение достаточного условия экстремума:
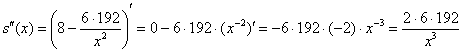
![]() (считать тут совсем не обязательно), значит, функция
(считать тут совсем не обязательно), значит, функция ![]() достигает минимума в точке
достигает минимума в точке ![]() .
.
Таким образом, размеры оптимального листа:
![]() ;
;
![]() ;
;
при этом минимальная площадь:
![]()
Ответ: ширина оптимальной страницы: ![]() , её высота:
, её высота: ![]() ; при этом минимальная площадь:
; при этом минимальная площадь: ![]()
Как видите, основная трудность состоит в том, чтобы разобраться в условии и составить нужную функцию. И в преодолении этой трудности здОрово помогает чертёж. Поэтому всегда стараемся выполнить схематический чертёж или хотя бы рисунок. Даже в таких простых случаях, как в Задаче № 3, не говоря уже о только что разобранном примере.
Следующее задание для самостоятельного решения:
Задача 5
В полукруг радиуса ![]() вписать прямоугольник наибольшего периметра
вписать прямоугольник наибольшего периметра
Просто и со вкусом. И снова несколько подсказок, которые полезно иметь в виду и при решении других задач:
! Во-первых, обратите внимание, что условие сформулировано в общем виде и величина ![]() считается известной. Если совсем тяжко, решите задачу с каким-нибудь конкретным значением радиуса, например, с радиусом
считается известной. Если совсем тяжко, решите задачу с каким-нибудь конкретным значением радиуса, например, с радиусом ![]() .
.
! Во-вторых, выполните схематический чертёж, который здесь очень прост: одна из сторон прямоугольника лежит на диаметре полукруга, а вершины противоположной стороны – на полуокружности. Очевидно, что в полукруг можно вписать бесконечно много прямоугольников и ваша задача найти такой, периметр которого максимален. Какую функцию нужно составлять, надеюсь, всем понятно. Подумайте, что удобнее обозначить за «икс» и, кроме того, освежите в памяти теорему Пифагора.
! В-третьих, задачу можно решить в разных стилях. Образец решения оформлен «исключительно геометрически», однако есть и такой вариант: начертить полукруг в декартовой системе координат – в верхней полуплоскости центром в точке ![]() . Далее составить уравнение окружности, выразить функцию верхней полуокружности и рассмотреть переменные координаты вершины прямоугольника, которая на этой полуокружности лежит. Более того, ввиду симметрии фигур относительно оси
. Далее составить уравнение окружности, выразить функцию верхней полуокружности и рассмотреть переменные координаты вершины прямоугольника, которая на этой полуокружности лежит. Более того, ввиду симметрии фигур относительно оси ![]() задачу можно решить в 1-й координатной четверти, т.е. изобразить лишь четвертинку круга (но затем не забыть удвоить одну из сторон прямоугольника). Кому как удобнее.
задачу можно решить в 1-й координатной четверти, т.е. изобразить лишь четвертинку круга (но затем не забыть удвоить одну из сторон прямоугольника). Кому как удобнее.
! И, в-четвёртых, эта задача о том, что иногда совсем не обязательно «разбивать лоб» о новый материал ;-) Если вам показался слишком сложным 2-й достаточный признак экстремума, то никто ведь не запрещает использовать 1-й достаточный признак – определите знаки первой производной слева и справа от критической точки ![]() на промежутке
на промежутке ![]() и сделайте вывод.
и сделайте вывод.
Приятного решения!
Наш урок в самом разгаре и настало время разобрать задачи, которые встречались в моей практике без преувеличения десятки раз:
Задача 6
Определите размеры открытого бассейна объемом ![]() , имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.
, имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.
Решение: представили бассейн. Квадратное дно. Стены. Размеры бассейна однозначно определяются его длиной и шириной, которые в данном случае совпадают (по условию дно квадратное) и глубиной (высотой стенки). Требуется найти такие размеры бассейна, чтобы на облицовку его поверхности ушло наименьшее количество материала (например, плитки). Из чего следует, что нам нужно составить функцию суммарной площади дна и 4 стен. Изобразим на чертеже развёртку бассейна – его дно и 4 стенки, которые аккуратно лежат рядышком:
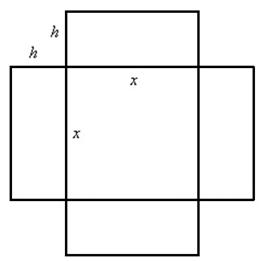
За «икс» здесь, конечно же, напрашивается обозначить сторону квадрата. Тогда площадь дна равна ![]() . Осталось выразить
. Осталось выразить ![]() – высоту стены и найти её площадь
– высоту стены и найти её площадь ![]() .
.
По условию, объём бассейна равняется 32 кубическим метрам. Даже не вспоминая и не разыскивая соответствующую формулу, нетрудно сообразить, что объём прямоугольного параллелепипеда – это произведение площади его «дна» на высоту:
![]()
В нашем случае: ![]() .
.
Составим функцию суммарной площади дна и четырёх одинаковых стен бассейна:
![]()
Найдем критические точки:
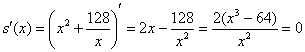
![]() – критическая точка.
– критическая точка.
Проверим выполнение достаточного условия экстремума:
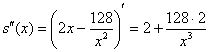
![]() , значит, функция
, значит, функция ![]() достигает минимума в точке
достигает минимума в точке ![]() .
.
Таким образом:
сторона оптимального бассейна ![]() ;
;
глубина ![]() ;
;
при этом минимальная площадь облицовки:
![]() .
.
Ответ: сторона оптимального бассейна: 4 м, глубина: 2 м; при этом минимальная площадь облицовки ![]() .
.
Кстати, это решение совсем не очевидно – так, например, на оптимальный вариант с успехом претендует «лягушатник» размером ![]() глубиной 1 метр, и «на глазок» очень трудно определить, что выгоднее – ведь площадь облицовки последнего лишь ненамного больше:
глубиной 1 метр, и «на глазок» очень трудно определить, что выгоднее – ведь площадь облицовки последнего лишь ненамного больше: ![]() . И да – надо отдать должное авторам задач за реалистичность, а то не так уж и редко получаются забавные результаты а-ля бассейн
. И да – надо отдать должное авторам задач за реалистичность, а то не так уж и редко получаются забавные результаты а-ля бассейн ![]() глубиной 32 метра, что называется, купайтесь и не квакайте =)
глубиной 32 метра, что называется, купайтесь и не квакайте =)
Аналогичная задача про суровые челябинские шпроты:
Задача 7
Каковы должны быть размеры консервной банки цилиндрической формы, чтобы на её изготовление пошло наименьшее количество материала, если объем банки 0,5 литра?
Но перед тем как решать, пожалуйста, ознакомьтесь с парой полезных замечаний:
Во-первых, литр – это единица объёма. Я специально заострил внимание на физике, поскольку на обывательском уровне литр очень часто неверно отождествляют с килограммом (единицей массы). Ощутите разницу – пол-литровая банка кильки и та же банка, наполненная гвоздями. Один литр равен одному кубическому дециметру или тысяче кубических сантиметров:
![]()
А теперь очень важный момент: так как размеры банки, очевидно, выразятся в сантиметрах, то 0,5 литра следует сразу перевести в кубические сантиметры!
К слову, что это за размеры? Цилиндр стандартно определяется радиусом основания ![]() и высотой
и высотой ![]() . Во-вторых. Освежим в памяти формулы:
. Во-вторых. Освежим в памяти формулы:
площадь круга: ![]()
площадь боковой поверхности цилиндра: ![]()
объём цилиндра: ![]()
И в который раз остановлюсь на важном принципе эффективного изучения математики: не зубрите формулы (без крайней необходимости, конечно). В частности, позабытую площадь боковой поверхности цилиндра несложно вывести даже в уме: представьте стенку консервной банки без дна и крышки. Сделайте вертикальный разрез и расправьте боковину на столе. В результате получился прямоугольник, одна из сторон которого, понятно, равна высоте банки ![]() , а другая – длине окружности
, а другая – длине окружности ![]() . Площадь же прямоугольника рассчитывается элементарно:
. Площадь же прямоугольника рассчитывается элементарно: ![]()
Решение проводится по аналогии с Задачей 6, примерный образец в конце урока.
Закрепим типовик своего рода обратными задачами:
Задача 8
Определить наибольшую вместимость цилиндрического бака, если его площадь поверхности (без крышки) должна равняться ![]()
Решение: в данном случае всё наоборот – известна площадь поверхности ![]() (если трудно, замените
(если трудно, замените ![]() конкретным числом) и требуется определить максимальный объём
конкретным числом) и требуется определить максимальный объём ![]() бака.
бака.
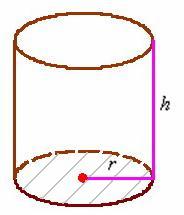
За «икс» обозначим… а зачем, собственно, лишние буквы? Ещё с первых уроков о производной многие поняли, что дифференцировать можно по любой переменной, и сейчас мы окончательно избавимся ото всех комплексов.
От какой переменной искать функцию объёма? В соответствующей формуле наиболее «наворочен» радиус, поэтому логично попытаться составить функцию ![]() , зависящую именно от него. Нужно только выразить высоту
, зависящую именно от него. Нужно только выразить высоту ![]() .
.
Сумма площадей дна (не забываем, что крышка отсутствует!) и боковой поверхности в точности равна известному значению: ![]() , откуда находим:
, откуда находим:
![]()
Таким образом:
![]()
Найдём критические точки:
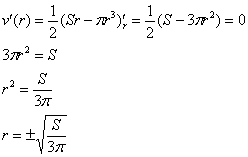
Геометрическому смыслу задачи, разумеется, удовлетворяет положительный корень ![]() . Проверим выполнение достаточного условия экстремума:
. Проверим выполнение достаточного условия экстремума:
![]()
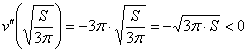 , значит, функция
, значит, функция ![]() достигает максимума в точке
достигает максимума в точке ![]() .
.
При этом высота бака:
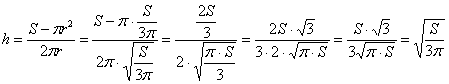
максимальный объём:
![]()
Ответ: радиус основания оптимального бака: ![]() , высота:
, высота: ![]() , при этом максимальный объём:
, при этом максимальный объём: ![]()
Решение в общем виде, бывает, кажется непривычным, однако оцените его универсальность – теперь достаточно лишь подставить конкретное значение площади и сразу рассчитать размеры оптимального цилиндра.
Успокоительное задание для самостоятельного решения:
Задача 9
Прямоугольный лист картона имеет размеры ![]() . Требуется вырезать по его углам такие квадраты, чтобы после загибания оставшихся кромок получилась коробка наибольшей вместимости.
. Требуется вырезать по его углам такие квадраты, чтобы после загибания оставшихся кромок получилась коробка наибольшей вместимости.
Краткое решение и ответ в конце урока.
Помимо рассмотренных выше геометрических объектов, на практике также можно встретить треугольники, трапеции, шары, конусы и т.д., но это более редкие гости (что касаемо забытых формул – справочники в помощь). К сожалению, нельзя объять необяътное, и поэтому в рамках этой статьи я ограничился самыми распространёнными примерами. И действительно, задач ведь придумать можно очень много – и всех их не перерешаешь, главное, чтобы вы хорошо поняли принципы и методы решения, которые я постарался изложить максимально пОлно и качественно.
Кроме того, существуют экстремальные задачи физического, химического, экономического и др. содержания, однако по причине отсутствия таковых в моей коллекции кот даже и не плакал. Но, понимая, что такое производная и обладая элементарной техникой дифференцирования, вы не должны испытать серьёзных затруднений с этими задачами, хотя для их решения, конечно, нужно разобраться и в самой физике/химии/экономике или иной предметной области.
Желаю успехов!
Решения и ответы:
Пример 3: Решение: найдем полупериметр прямоугольника: ![]() . Обозначим через
. Обозначим через ![]() длину стороны прямоугольника (любую). Тогда
длину стороны прямоугольника (любую). Тогда ![]() – длина смежной стороны:
– длина смежной стороны:
Составим функцию площади прямоугольника:
![]() .
.
Найдем критические точки:
![]()
![]() – критическая точка.
– критическая точка.
Проверим выполнение достаточного условия экстремума.
![]() , значит, функция
, значит, функция ![]() достигает максимума в точке
достигает максимума в точке ![]() .
.
Таким образом ![]() – оптимальная длина стороны прямоугольника, длина смежной стороны:
– оптимальная длина стороны прямоугольника, длина смежной стороны: ![]() ; при этом максимальная площадь:
; при этом максимальная площадь:
![]()
Ответ: оптимальный прямоугольник представляет собой квадрат со стороной ![]() ; при этом максимальная площадь:
; при этом максимальная площадь: ![]() .
.
Пример 5: Решение: выполним чертёж:
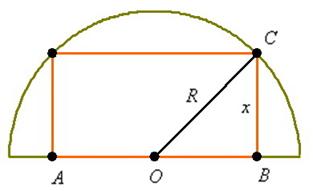
Пусть ![]() (как вариант, за «икс» можно обозначить
(как вариант, за «икс» можно обозначить ![]() или даже
или даже ![]() ).
).
Рассмотрим прямоугольный ![]() . По теореме Пифагора:
. По теореме Пифагора:
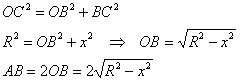
Составим функцию периметра прямоугольника:
![]()
Найдём критические точки:
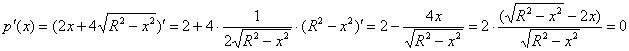 Решим простейшее иррациональное уравнение:
Решим простейшее иррациональное уравнение:
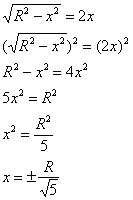
Уравнению ![]() удовлетворяет корень
удовлетворяет корень ![]() (корень же
(корень же ![]() появился в результате возведения обеих частей в квадрат и является посторонним).
появился в результате возведения обеих частей в квадрат и является посторонним).
Проверим выполнение достаточного условия экстремума.
Способ первый: определим знаки производной:
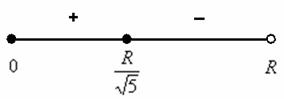
Примечание: используем стандартный метод интервалов: в производную ![]() подставляем какое-нибудь значение, лежащее левее точки
подставляем какое-нибудь значение, лежащее левее точки ![]() , например,
, например, ![]() и подставляем какое-нибудь значение из правого интервала – проще всего взять
и подставляем какое-нибудь значение из правого интервала – проще всего взять ![]() .
.
Вывод: функция ![]() достигает максимума в точке
достигает максимума в точке ![]() .
.
Способ второй:
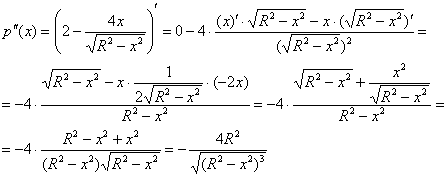
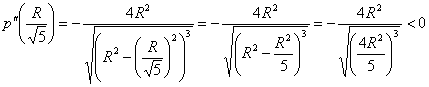 , значит, функция
, значит, функция ![]() достигает максимума в точке
достигает максимума в точке ![]() .
.
Таким образом, размеры оптимального прямоугольника:
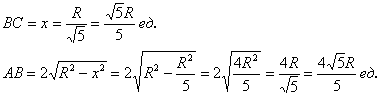
При этом максимальный периметр:
![]()
Ответ: оптимальный прямоугольник имеет размеры ![]() , при этом максимальный периметр:
, при этом максимальный периметр: ![]()
Пример 7: Решение: составим функцию площади полной поверхности цилиндра ![]() , зависящую от его радиуса. Пусть
, зависящую от его радиуса. Пусть ![]() – радиус дна (и крышки) консервной банки:
– радиус дна (и крышки) консервной банки:
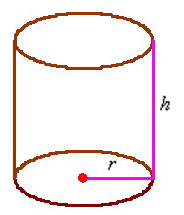
Тогда площадь дна: ![]() . Столько же и площадь крышки.
. Столько же и площадь крышки.
По условию объём консервной банки равен ![]() :
:
![]()
Выразим через ![]() площадь боковой поверхности банки:
площадь боковой поверхности банки:
![]()
Площадь полной поверхности банки равна сумме площадей дна, крышки и боковой поверхности:
![]()
Найдём критические точки:
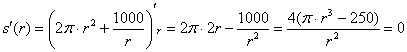
![]() – критическая точка.
– критическая точка.
Проверим выполнение достаточного условия экстремума:
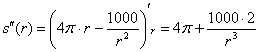
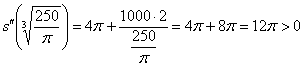 , значит, функция
, значит, функция ![]() достигает минимума в точке
достигает минимума в точке ![]() .
.
Высота оптимальной банки:
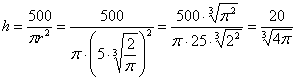
Ответ: радиус основания оптимальной банки: ![]() , её высота:
, её высота: ![]()
Пример 9: Решение: пусть ![]() – сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят
– сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят ![]() и
и ![]() :
:
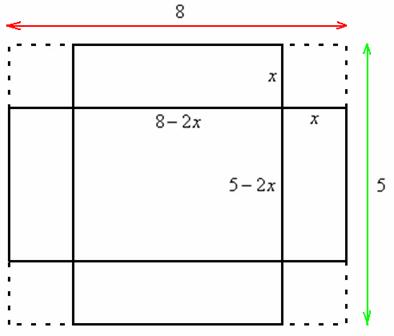
Составим функцию объёма коробки:
![]()
Найдём критические точки:
![]()
Решим квадратное уравнение:
![]()
![]() – критические точки. Второе значение не удовлетворяет геометрическому смыслу задачи, поскольку суммарная длина отреза сверху и снизу
– критические точки. Второе значение не удовлетворяет геометрическому смыслу задачи, поскольку суммарная длина отреза сверху и снизу ![]() (ширины листа).
(ширины листа).
Проверим выполнение достаточного условия экстремума:
![]()
![]() , значит, функция
, значит, функция ![]() достигает максимума в точке
достигает максимума в точке ![]() .
.
Ответ: размеры оптимальной коробки:
![]() – высота (сторона вырезаемых по углам квадратов);
– высота (сторона вырезаемых по углам квадратов);
![]() – длина;
– длина;
![]() – ширина;
– ширина;
при этом максимальный объем:
![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
