
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Поверхностные интегралы. Понятие и примеры решений
Наконец-то длительные каникулы подошли к концу, и я рад приветствовать ценителей интегрального исчисления на новом уроке! Сегодня мы зайдём немножко в дебри темы, которые освещены далеко не во всех учебниках по математическому анализу. И это большое упущение, поскольку задачи на вычисление поверхностных интегралов встречаются даже у студентов-заочников. Что тут сказать… – Пробелы есть, пробелы нужно закрывать!
Итак, что же такое поверхностный интеграл? Из самого названия следует, что здесь речь идёт об объединении (интегрировании) некоторой величины по поверхности. Представьте лесную полянку с муравьями…, где-то их больше, где-то меньше, и цель поверхностного интегрирования состоит в том, чтобы вычислить суммарную «муравьиную массу» по поверхности поляны.
И этот «детский» пример не так далёк от сути – поверхностные интегралы получили широчайшее распространение в физике, где часто возникает надобность подсчитать ту или иную физическую величину по поверхности. Но коль скоро сайт посвящён математике, то в рамках данного урока я не буду рассматривать все эти приложения, а остановлюсь на технической стороне вопроса – чтобы у вас не возникало трудностей именно с вычислением поверхностных интегралов.
Начнём с условностей и обозначений.
Поверхности. В практических задачах, как правило, встречаются «обычные», а также кусочно-гладкие поверхности, состоящие из «кусков» плоскостей, цилиндров, параболоидов и иже с ними. Далее по умолчанию будем подразумевать только «хорошие» ограниченные (грубо говоря, не бесконечные) поверхности, позволяющие беспроблемно интегрировать. Система координат по дефолту прямоугольная декартова ![]() – тоже удобная и хорошая.
– тоже удобная и хорошая.
Поверхность обычно обозначают буквой ![]() или
или ![]() . Последний вариант хоть и распространён, но не слишком хорош, так как ассоциируется с площадью; «омега» сложнА для написания, а посему поверхность условимся обозначать буквой
. Последний вариант хоть и распространён, но не слишком хорош, так как ассоциируется с площадью; «омега» сложнА для написания, а посему поверхность условимся обозначать буквой ![]() .
.
Поверхностный интеграл по поверхности ![]() обозначают удвоенным значком интеграла:
обозначают удвоенным значком интеграла:
![]()
И здесь сразу возникает вопрос: поверхность – она же в пространстве, так почему интеграла только два? Дело в том, что пространственная поверхность – это объект двумерный. Простейшее доказательство проведём с помощью полюбившегося наглядного пособия =) Расстелите на полу одеяло и задайте на нём, например, декартову систему ![]() . Сколько координат нужно указать, чтобы определить любую точку одеяла? Две. Теперь поднимите одеяло и произвольно изогните его в пространстве.
. Сколько координат нужно указать, чтобы определить любую точку одеяла? Две. Теперь поднимите одеяло и произвольно изогните его в пространстве.
Ещё более наглядный пример – наш земной шар эллипсоид. Любая точка его поверхности однозначно определяется двумя координатами (широтой и долготой).
Кстати, если поверхность ![]() ограничена, замкнута и лежит в плоскости
ограничена, замкнута и лежит в плоскости ![]() , то
, то ![]() представляет собой не что иное, как старый-знакомый двойной интеграл.
представляет собой не что иное, как старый-знакомый двойной интеграл.
Ну а с другой точки зрения, поверхностный интеграл – это пространственный аналог криволинейного интеграла, и если у вас после этих фраз отлегло от сердца, то можете смело читать дальше =)
…правильно догадываетесь – поверхностные интегралы тоже бывают первого рода и второго рода.
Поверхностные интегралы первого рода
Рассмотрим некоторую поверхность ![]() . Из чего она состоит? Из точек с координатами «икс, игрек, зет». Отлично.
. Из чего она состоит? Из точек с координатами «икс, игрек, зет». Отлично.
Пусть функция трёх переменных ![]() определена в каждой точке данной поверхности. Что это значит? Это значит, что каждой точке
определена в каждой точке данной поверхности. Что это значит? Это значит, что каждой точке ![]() поверхности ставится в соответствие определённое число
поверхности ставится в соответствие определённое число ![]() – образно говоря, «муравей» той или иной степени «упитанности», который «сидит» на бесконечно малом участке
– образно говоря, «муравей» той или иной степени «упитанности», который «сидит» на бесконечно малом участке ![]() данной поверхности.
данной поверхности.
Наверное, многие предчувствуют дальнейшее развитие темы. Согласно общему принципу интегрирования, интеграл ![]() объединяет этих «муравьёв» по всем бесконечно малым площадям
объединяет этих «муравьёв» по всем бесконечно малым площадям ![]() поверхности
поверхности ![]() .
.
И нетрудно понять, что при ![]() он в точности равен площади самой поверхности:
он в точности равен площади самой поверхности:
![]()
Как решать поверхностные интегралы 1-го рода?
Пример 1
С помощью поверхностного интеграла найти площадь фрагмента плоскости ![]() , расположенного в 1 октанте.
, расположенного в 1 октанте.
…извращение, конечно, но что поделать =)
Решение: сначала выполним чертёж. В большинстве случаев без него никак. Для этого запишем уравнение плоскости в отрезках:
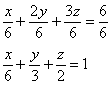
По причине нахлынувшей ностальгии все чертежи этого урока я выполню от руки. Да и не только по этой – думается, ручное построение поверхностей будет актуально ещё достаточно долго:
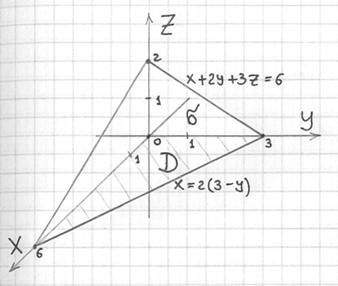
По условию, площадь треугольника ![]() нужно найти с помощью поверхностного интеграла 1-го рода:
нужно найти с помощью поверхностного интеграла 1-го рода:
![]()
Если поверхность задана функцией двух переменных ![]() , то поверхностный интеграл можно свести к двойному интегралу по формуле:
, то поверхностный интеграл можно свести к двойному интегралу по формуле:
![]() , где
, где ![]() – проекция поверхности
– проекция поверхности ![]() на плоскость
на плоскость ![]() . Занесите в свой справочник.
. Занесите в свой справочник.
В нашем случае речь идёт о площади и поэтому формула упрощается:
![]() (прерываемся для промежуточных действий)
(прерываемся для промежуточных действий)
Перепишем уравнение плоскости в функциональном виде:
![]()
и найдём частные производные первого порядка, они здесь элементарные:
![]()
продолжаем:
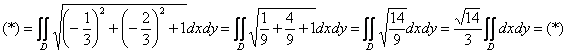
С областью ![]() (на чертеже заштрихована) трудностей нет – остановлюсь лишь на том, как найти уравнение прямой, которая лежит в плоскости
(на чертеже заштрихована) трудностей нет – остановлюсь лишь на том, как найти уравнение прямой, которая лежит в плоскости ![]() . Для этого в уравнении плоскости
. Для этого в уравнении плоскости ![]() обнуляем «лишнюю» зетовую переменную:
обнуляем «лишнюю» зетовую переменную:
![]()
откуда удобно выразить:
![]()
Двумерный чертёж настоятельно рекомендую даже читателям с высоким уровнем подготовки, ибо «проглючить» тут может как дважды два:
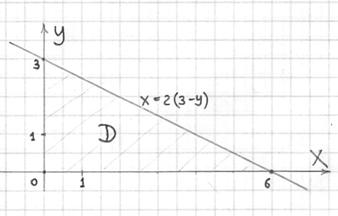
Ну и очевидно, что порядок обхода области будет таким:
![]()
После чего решение выходит на финишную прямую:

Ответ: ![]()
Желающие могут найти пару подходящих векторов и проверить результат с помощью векторного произведения.
Но это ещё далеко не всё. Зададимся следующим вопросом: а почему поверхность нужно проецировать именно на плоскость ![]() ? Чем другие координатные плоскости и другие переменные хуже? Да ничем! Давайте окончательно отбросим все комплексы и освоим универсальную технику интегрирования:
? Чем другие координатные плоскости и другие переменные хуже? Да ничем! Давайте окончательно отбросим все комплексы и освоим универсальную технику интегрирования:
Формула вторая: если поверхность ![]() выражена функцией
выражена функцией ![]() , то:
, то:
![]() , где
, где ![]() – проекция данной поверхности на плоскость
– проекция данной поверхности на плоскость ![]() .
.
В нашем случае:
![]()
Перепишем уравнение плоскости в виде:
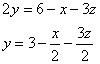
и возьмём частные производные:
![]()
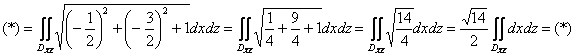
Теперь в уравнении плоскости обнулим «лишнюю» игрековую координату, выяснив тем самым уравнение прямой, которая лежит в плоскости ![]() :
:
![]()
Выполним чертёж проекции ![]() :
:
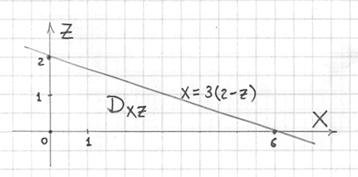
(на пространственном чертеже это левый «стоячий» треугольник)
Порядок обхода области:
![]()
таким образом:
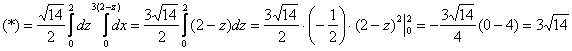
Что мы и ожидали увидеть.
Самостоятельно запишите формулу вычисления поверхностного интеграла для случая, когда поверхность выражена функцией ![]() и решите задачу третьим способом – проецированием поверхности на плоскость
и решите задачу третьим способом – проецированием поверхности на плоскость ![]()
Зачем нужна эта экзотика?
Нужна. И более того, не такая уж это и экзотика. В некоторых задачах проецирование на «родную» плоскость ![]() сопряжено с трудностями или вообще недопустимо (когда поверхность параллельна оси
сопряжено с трудностями или вообще недопустимо (когда поверхность параллельна оси ![]() ). Или получается трудный интеграл. И поэтому всегда нужно держать на заметке, что существуют альтернативные пути!
). Или получается трудный интеграл. И поэтому всегда нужно держать на заметке, что существуют альтернативные пути!
Следующее задание для самостоятельного решения:
Пример 2
С помощью поверхностного интеграла вычислить площадь поверхности ![]() , расположенную в верхнем полупространстве.
, расположенную в верхнем полупространстве.
Тот редкий случай, когда можно обойтись без чертежа – слишком уж каноничен параболоид. Следует отметить, что в этом примере выгодно именно «классическое» интегрирование с проецированием поверхности на плоскость ![]() . Кстати, результат будет любопытно сравнить с ответом Примера 2 статьи Площадь поверхности вращения.
. Кстати, результат будет любопытно сравнить с ответом Примера 2 статьи Площадь поверхности вращения.
Добавим в наш интеграл какую-нибудь интересную функцию…. Посвящается «математической» доменной зоне и Гуглу в частности:)
Пример 3
Вычислить интеграл ![]() , где
, где ![]() – фрагмент конической поверхности
– фрагмент конической поверхности ![]() , заключенный между плоскостями
, заключенный между плоскостями ![]() .
.
Решение: порядок построения чертежа подробно рассмотрен в статье о поверхностях, но, тем не менее, кратко повторю: на высоте ![]() данная плоскость пересекает конус по:
данная плоскость пересекает конус по:
![]() – окружности единичного радиуса:
– окружности единичного радиуса:
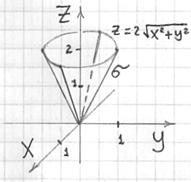
![]() -«колпак» проще спроецировать на «стандартную» плоскость:
-«колпак» проще спроецировать на «стандартную» плоскость:
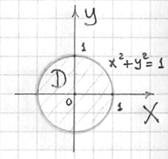
и воспользоваться формулой
![]()
Верхнюю часть конуса задаёт функция:
![]()
Найдём её частные производные:
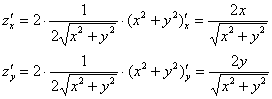
И здесь сразу удобно упростить корень:
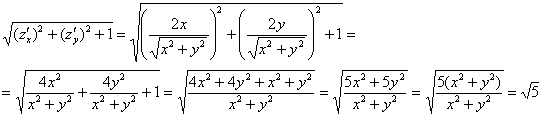
Таким образом, по формуле (см. выше):
![]()
Тут, конечно, лучше перейти к полярным координатам:
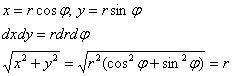
И из «плоского» чертежа очевиден порядок обхода:
![]()
Постараемся ничего не упустить:
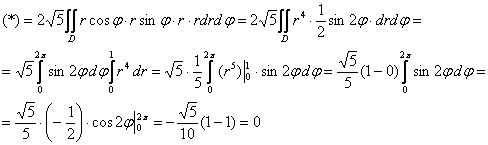
Ответ: ![]()
Может ли поверхностный интеграл равняться нулю? Конечно. И отрицательному числу тоже. Ведь подынтегральная функция ![]() может принимать любые значения.
может принимать любые значения.
Рассмотрим два альтернативных пути. Вкратце разберу порядок действий:
Способ второй. Проецируем конус на плоскость ![]() (получится треугольник) и используем формулу
(получится треугольник) и используем формулу ![]() ,
,
причём, интеграл придётся представить в виде суммы двух интегралов:
![]() ,
,
где ![]() – это левая часть конуса, которую нужно выразить функцией:
– это левая часть конуса, которую нужно выразить функцией:
![]()
а ![]() – его правая часть:
– его правая часть:
![]()
И противоположные «игрековые» знаки приводят к забавной коллизии – в результате интегралы взаимоуничтожаются и сразу получается ноль (если не понятно, почему так, начните решать). А казалось, это был совершенно нерациональный путь! Но то, конечно, частный счастливый случай.
Здесь, кстати, мы столкнулись со свойством аддитивности, которое наряду со свойством линейности, разумеется, справедливо и для поверхностных интегралов. Иными словами, поверхность можно разделить на несколько кусков, вычислить интеграл по каждому из них, после чего просуммировать результаты.
Способ третий. Проецируем конус на плоскость ![]() (тоже получится треугольник) и используем формулу
(тоже получится треугольник) и используем формулу ![]()
Аналогично – интеграл представляем как сумму интегралов по ближней ![]() и по дальней
и по дальней ![]() от нас части конуса; результаты так же взаимоуничтожаются и получается ноль.
от нас части конуса; результаты так же взаимоуничтожаются и получается ноль.
Рассмотренная поверхность тоже «хорошо» проецируется на все координатные плоскости, однако так бывает далеко не всегда. Не такая уж редкость, когда в нашем распоряжении оказываются два, а то и единственный путь решения. Соответствующие примеры будут на уроке Поток векторного поля. Но пока с ними повременим.
Следующее задание для самостоятельного решения:
Пример 4
Вычислить интеграл ![]() , где
, где ![]() – часть плоскости
– часть плоскости ![]() , ограниченная координатными плоскостями. Выполнить чертёж.
, ограниченная координатными плоскостями. Выполнить чертёж.
Моя версия решения в конце урока.
В рамках данной статьи я не буду рассматривать общую формулу вычисления поверхностного интеграла 1-го рода для параметрически заданной поверхности. По той причине, что в большинстве учебных курсов всё дело ограничивается частными декартовыми формулами. Однако читателям-«технарям» просто необходимо ознакомиться с этим материалом – соответствующую информацию можно найти здесь (попроще) и здесь (посложнее). Там же, к слову, есть развёрнутая теория и дополнительные примеры.
И в заключение параграфа коротко о «главном» физическом смысле рассмотренного интеграла:
если поверхность ![]() представляет собой тонкую оболочку (железную, пластмассовую и т.д.; не обязательно однородную), а функция
представляет собой тонкую оболочку (железную, пластмассовую и т.д.; не обязательно однородную), а функция ![]() характеризует её плотность в каждой точке
характеризует её плотность в каждой точке ![]() , то поверхностный интеграл 1-го рода численно равен массе данной оболочки:
, то поверхностный интеграл 1-го рода численно равен массе данной оболочки: ![]() .
.
Логично. У криволинейного интеграла 1-го рода, напоминаю, была масса кривой.
И никаких насекомых =)
Поверхностные интегралы второго рода
Здесь опять прослеживается аналогия с криволинейными интегралами. Если в поверхностном интеграле ![]() значения функции
значения функции ![]() умножаются на бесконечно малые кусочки
умножаются на бесконечно малые кусочки ![]() самой поверхности (кусочки площади), то у поверхностных интегралов 2-го рода интегрирование осуществляется по проекциям этих кусков на координатные плоскости. В случае проецирования на плоскость
самой поверхности (кусочки площади), то у поверхностных интегралов 2-го рода интегрирование осуществляется по проекциям этих кусков на координатные плоскости. В случае проецирования на плоскость ![]() площадь таковой бесконечно малой проекции символически обозначают произведением
площадь таковой бесконечно малой проекции символически обозначают произведением ![]() .
.
Второе принципиальное отличие состоит в том, что интегрирование ведётся по ориентированной поверхности. Что это значит? Накройтесь одеялом и представьте, что его «протыкает» ось ![]() (остриём вверх).
(остриём вверх).
Одну сторону поверхности считают верхней или положительной, обозначим её через ![]() , другую сторону – нижней или отрицательной (
, другую сторону – нижней или отрицательной (![]() ). Таким образом можно составить ДВА поверхностных интеграла 2-го рода, причём:
). Таким образом можно составить ДВА поверхностных интеграла 2-го рода, причём:
![]()
Что называется, по одну сторону одеяла Вы есть, а по другую Вас нет =) И тут даже скептики согласятся, что разница существует.
Во многих случаях удобно «безликое» обозначение ![]() – со словесным комментарием, о какой стороне поверхности идёт речь. Но более строго стороны принято определять единичными векторами нормали (вспоминаем, что такое вектор нормали к поверхности).
– со словесным комментарием, о какой стороне поверхности идёт речь. Но более строго стороны принято определять единичными векторами нормали (вспоминаем, что такое вектор нормали к поверхности).
У верхней стороны одеяла эти векторы образуют с осью ![]() острые углы, у нижней стороны – тупые. Если поверхность параллельна оси
острые углы, у нижней стороны – тупые. Если поверхность параллельна оси ![]() , то угол прямой, сама поверхность проецируется в линию и оба интеграла равны нулю.
, то угол прямой, сама поверхность проецируется в линию и оба интеграла равны нулю.
Однако это только треть айсберга.
Кусочки ориентированной поверхности можно спроецировать на координатные плоскости ![]() , провести аналогичные рассуждения и получить ещё две пары поверхностных интегралов 2-го рода:
, провести аналогичные рассуждения и получить ещё две пары поверхностных интегралов 2-го рода:
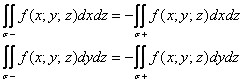
Здесь значком ![]() обозначают ту сторону поверхности, которая «смотрит» в направлении осей
обозначают ту сторону поверхности, которая «смотрит» в направлении осей ![]() и
и ![]() соответственно.
соответственно.
Но то были шутки – на практике наибольшую популярность снискал «комбинированный» интеграл ![]() .
.
! Слагаемые не переставляем, буквы не меняем! И другим не даём. Это стандарт.
Начинаем отрабатывать технику интегрирования:
Пример 5
Вычислить интеграл ![]() , где
, где ![]() – верхняя сторона плоскости
– верхняя сторона плоскости ![]() , расположенная в 1 октанте.
, расположенная в 1 октанте.
Решение: перепишем уравнение плоскости в отрезках: ![]() и изобразим уже привычную картину. Кроме того, добавим единичный нормальный вектор плоскости, указывающий нужное направление:
и изобразим уже привычную картину. Кроме того, добавим единичный нормальный вектор плоскости, указывающий нужное направление:
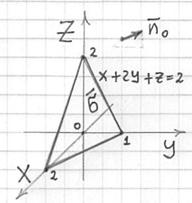
Пожалуйста, ничего не пропускайте! – тут много важного:
Поверхностный интеграл 2-го рода можно решить двумя способами
Способ первый. Прямое сведение к двойному интегралу.
Для этого удобно использовать свойство линейности:
![]() – чтобы с каждым интегралом разделаться по отдельности:
– чтобы с каждым интегралом разделаться по отдельности:
1) ![]()
Правило: если нормальные векторы к поверхности ![]() образуют с положительной «иксовой» полуосью
образуют с положительной «иксовой» полуосью ![]() острые углы, то интеграл такого вида сводится к двойному интегралу по формуле:
острые углы, то интеграл такого вида сводится к двойному интегралу по формуле:
![]() , где
, где ![]() – функция поверхности, а
– функция поверхности, а ![]() – проекция этой поверхности на плоскость
– проекция этой поверхности на плоскость ![]() .
.
В противном случае (когда углы тупые): ![]()
Если поверхность параллельна оси ![]() , то
, то ![]() . Конец правила.
. Конец правила.
! Правила и формулы переписывайте на бумагу!
Чтобы не возвращаться за ними вновь и вновь.
В нашем случае ![]() – острый (см. чертёж выше), поэтому используем первую формулу. Выражаем нужную функцию поверхности
– острый (см. чертёж выше), поэтому используем первую формулу. Выражаем нужную функцию поверхности ![]() , и понеслось:
, и понеслось:
![]()
Найдём линию пересечения плоскости ![]() с координатной плоскостью
с координатной плоскостью ![]() :
:
![]() и изобразим проекцию
и изобразим проекцию ![]() :
:
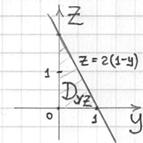
Выберем следующий порядок обхода области:
![]()
Таким образом:
Второй и третий интегралы решаются аналогично:
2) ![]()
Правило: если нормальные векторы к поверхности ![]() образуют с положительной полуосью
образуют с положительной полуосью ![]() острые углы, то
острые углы, то ![]() ; если тупые, то:
; если тупые, то: ![]() , где
, где ![]() проекция поверхность на плоскость
проекция поверхность на плоскость ![]() . Если же поверхность параллельна оси
. Если же поверхность параллельна оси ![]() , то
, то ![]() .
.
В нашем случае ![]() – острый, поэтому нужно использовать первую формулу:
– острый, поэтому нужно использовать первую формулу:
Выражаем: ![]() и раскручиваем второй интеграл:
и раскручиваем второй интеграл:
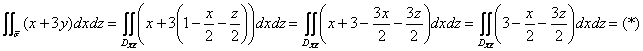
Найдём линию пересечения поверхности с координатной плоскостью ![]() :
:
![]() и изобразим область
и изобразим область ![]() :
:
Порядок обхода области:
![]()
Громоздкие вычисления надёжнее оформлять «простынёй»,
одна строка – одно действие:

3) И, наконец, наш «родной» интеграл ![]()
Вместе с родным правилом:) если нормальные векторы к поверхности ![]() образуют с положительной полуосью
образуют с положительной полуосью ![]() острые углы, то
острые углы, то ![]() ; если тупой, то
; если тупой, то ![]() ; если поверхность параллельна оси
; если поверхность параллельна оси ![]() , то
, то ![]() .
.
Очевидно, что у нас снова «острый» случай, и задача облегчается тем, что в подынтегральной функции отсутствует переменная «зет», а значит, уравнение плоскости ![]() не нужно представлять в виде
не нужно представлять в виде ![]() .
.
Сразу находим проекцию и решаем интеграл «одной строкой»:
![]()
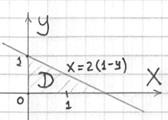
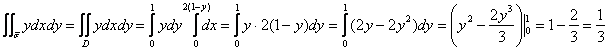
Надо же, одной строкой и вышло =)
Осталось просуммировать полученные результаты:
Ответ: ![]()
Ввиду очевидного свойства ![]() этот же интеграл по нижней стороне поверхности будет равняться «минус пяти».
этот же интеграл по нижней стороне поверхности будет равняться «минус пяти».
Надо сказать, мы прорешали универсальное задание, поскольку на практике вам по отдельности могут предложить такой: ![]() , либо такой
, либо такой ![]() , либо такой
, либо такой ![]() интеграл. Или же сумму любых двух частей. Поэтому труды и усидчивость были и будут (!) не напрасны!
интеграл. Или же сумму любых двух частей. Поэтому труды и усидчивость были и будут (!) не напрасны!
Второй способ решения. Поверхностный интеграл 2-го рода можно свести к поверхностному интегралу 1-го рода по следующей формуле:
![]() , где:
, где:
![]() – векторная функция, которая каждой точке
– векторная функция, которая каждой точке ![]() ориентированной поверхности
ориентированной поверхности ![]() ставит в соответствие несвободный вектор
ставит в соответствие несвободный вектор ![]() с началом в данной точке. В нашем случае:
с началом в данной точке. В нашем случае: ![]()
![]() – векторная функция, которая каждой точке
– векторная функция, которая каждой точке ![]() опять же ориентированной поверхности
опять же ориентированной поверхности ![]() ставит в соответствие единичный нормальный вектор к данной стороне поверхности в данной точке. Если поверхность задана функцией двух переменных
ставит в соответствие единичный нормальный вектор к данной стороне поверхности в данной точке. Если поверхность задана функцией двух переменных ![]() , то оную функцию можно составить по формуле:
, то оную функцию можно составить по формуле:
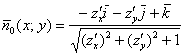 – для верхней (положительной) стороны поверхности, или:
– для верхней (положительной) стороны поверхности, или:
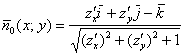 – для нижней (отрицательной) стороны.
– для нижней (отрицательной) стороны.
Следует заметить, что все нормальные векторы, наоборот – свободны.
Так как в нашем примере поверхность плоская, то во всех её точках вектор ![]() будет одним и тем же (на трёхмерном чертеже я изобразил его один раз). И действительно:
будет одним и тем же (на трёхмерном чертеже я изобразил его один раз). И действительно:
![]()
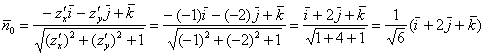 – один и тот же вектор для всех точек поверхности
– один и тот же вектор для всех точек поверхности ![]() .
.
Теперь по обычной формуле вычислим скалярное произведение, при этом константу нормального вектора удобно сразу вынести за скобки:
![]()
Таким образом, по указанной выше формуле:
![]()
Поверхностный интеграл 1-го рода, как вы помните, можно вычислить тремя способами, …но я уж не буду таким извергом =) Ограничимся проецированием поверхности ![]() (уже не ориентированной!) на плоскость
(уже не ориентированной!) на плоскость ![]() и формулой:
и формулой:
![]()
Функция ![]() – готовенькая, да и корень тоже вычислен:
– готовенькая, да и корень тоже вычислен:
![]()
Скопирую для наглядности проекцию:
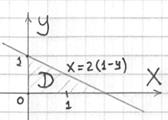
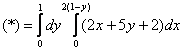
Интеграл таки лучше взять поэтапно:
1)
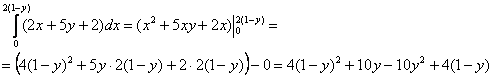
2)

Ответ: ![]()
Может показаться, что второй способ легче первого, но так бывает далеко не всегда
И немного забегая вперёд, сообщу, что рассмотренное в задаче множество векторов ![]() образует векторное поле, а сам интеграл
образует векторное поле, а сам интеграл ![]() получил название Поток векторного поля. Очень хочется рассказать подробнее, но я пока оставлю за кадром эти интереснейшие понятия и примеры из жизни.
получил название Поток векторного поля. Очень хочется рассказать подробнее, но я пока оставлю за кадром эти интереснейшие понятия и примеры из жизни.
Для самостоятельного решения:
Пример 6
Вычислить интеграл ![]() по верхней стороне
по верхней стороне ![]() плоскости
плоскости ![]() , ограниченной координатными плоскостями.
, ограниченной координатными плоскостями.
Нет, это вовсе не занудство, треугольник – самая распространённая поверхность, которая встречается чуть ли не в половине тематических задач.
Постарайтесь решить интеграл обоими способами: в первом случае следует проявить повышенное внимание при выборе формулы (см. правила Примера 5), а во втором нужно иметь в виду, что «недостающие» компоненты векторной функции равны нулю.
Краткое решение и ответ в конце урока.
Но это ещё не всё! Продолжаем:
Пример 7
Вычислить интеграл ![]() по внешней стороне
по внешней стороне ![]() полусферы
полусферы ![]() , расположенной в верхнем полупространстве.
, расположенной в верхнем полупространстве.
Формулировки внешняя сторона и внутренняя сторона распространены и интуитивно понятны, но они таят в себе немало опасностей. Давайте разбираться, в чём дело:
Решение: чертёж здесь очень прост:
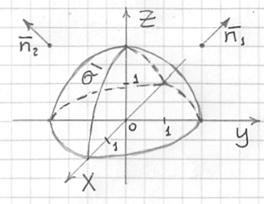
И первое отличие касается нормальных векторов поверхности . У каждой точки полусферы он свой (в качестве примера я изобразил пару штук).
Решим задачу первым способом:
![]()
1) Вычислим ![]()
И тут нас поджидает сюрприз: нормальные векторы полусферы образуют с полуосью ![]() как острые, так и тупые углы. Что делать?
как острые, так и тупые углы. Что делать?
В силу свойства аддитивности, поверхностный интеграл можно (и нужно) разделить на две части:
Для ближней к нам четвертинки сферы, которая выражается функцией ![]() , углы будут острыми и поэтому:
, углы будут острыми и поэтому:
![]()
Для дальней четвертинки ![]() эти углы тупы, и поэтому там следует применить формулу с «минусом»:
эти углы тупы, и поэтому там следует применить формулу с «минусом»:
![]()
Таким образом:
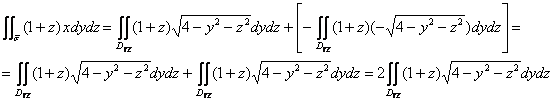
где ![]() – проекция полусферы на плоскость
– проекция полусферы на плоскость ![]() .
.
2) С интегралом ![]() ситуация такая же: нормальные векторы правой четвертинки
ситуация такая же: нормальные векторы правой четвертинки ![]() (например,
(например, ![]() ) образуют с полуосью
) образуют с полуосью ![]() острые углы, а нормальные векторы левой четвертинки
острые углы, а нормальные векторы левой четвертинки ![]() (например,
(например, ![]() ) – тупые углы.
) – тупые углы.
Следовательно:
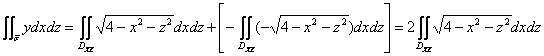 , где
, где ![]() – тоже полукруг радиуса 2, но уже в плоскости
– тоже полукруг радиуса 2, но уже в плоскости ![]() .
.
3) С интегралом ![]() ситуация чуть проще: т.к. нормальные векторы образуют с полуосью
ситуация чуть проще: т.к. нормальные векторы образуют с полуосью ![]() острые углы, то для соответствующей функции
острые углы, то для соответствующей функции ![]() используем «плюсовую» формулу:
используем «плюсовую» формулу:
![]() , где
, где ![]() – круг радиуса 2.
– круг радиуса 2.
К слову, для полной сферы, поверхностный интеграл нужно дробить и в этом пункте.
Осталось вычислить интегралы и просуммировать результаты. Но повторять что-то не хочется =)
Конечно, здесь проще второй способ. Хотя, справедливости ради, ненамного:
![]()
Запишем функцию векторного поля: ![]()
Поскольку нормальные векторы поверхности ![]() образуют с полуосью
образуют с полуосью ![]() острые углы, то для построения соответствующей векторной функции используем формулу:
острые углы, то для построения соответствующей векторной функции используем формулу:
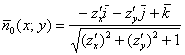
В данном случае:
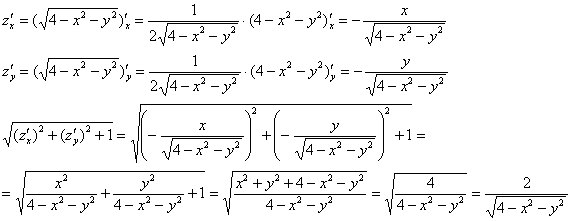
Таким образом:
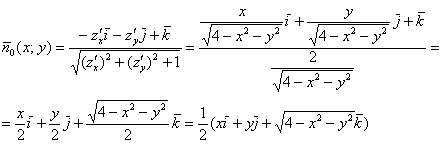
Еще раз повторим смысл этих функций: каждой точке ![]() полусферы, ставится в соответствие несвободный вектор
полусферы, ставится в соответствие несвободный вектор ![]() , «торчащий» из этой точки, и единичный нормальный вектор
, «торчащий» из этой точки, и единичный нормальный вектор ![]() (свободный), указывающий ориентацию поверхности в данной точке.
(свободный), указывающий ориентацию поверхности в данной точке.
Вычислим скалярное произведение:
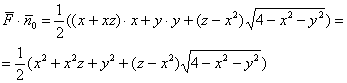
Сводим дело к поверхностному интегралу 1-го рода, не забывая, что ![]() :
:
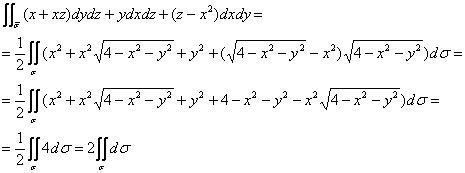
Самостоятельно доведите решение до конца по формуле ![]() , ну а я воспользуюсь тем фактом, что
, ну а я воспользуюсь тем фактом, что ![]() равен площади поверхности
равен площади поверхности ![]() . Как известно, площадь поверхности сферы равна
. Как известно, площадь поверхности сферы равна ![]() , следовательно, площадь нашей полусферы радиуса
, следовательно, площадь нашей полусферы радиуса ![]() составляет:
составляет: ![]()
Ответ: ![]()
Соответственно, интеграл по нижней стороне этой же полусферы будет равняться ![]() .
.
Несложный и познавательный пример для самостоятельного изучения:
Пример 8
Вычислить поверхностный интеграл ![]() по внутренней стороне параболического цилиндра
по внутренней стороне параболического цилиндра ![]() . Выполнить чертёж.
. Выполнить чертёж.
В конце страницы есть решение обоими способами.
Ну а теперь пришло время поздравить всех выживших с успешным (надеюсь) приобретением новых знаний и навыков. И это действительно достижение, поскольку данная статья является одной из самых сложных на сайте.
На очереди интереснейшая Теория поля, к которой мы плавно подходили в ходе изучения криволинейных и поверхностных интегралов. Не пропустите!
Решения и ответы:
Пример 2: Решение: выполним чертежи:
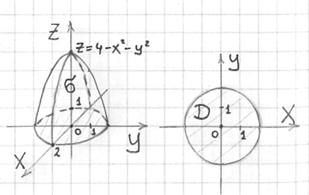
Площадь искомой поверхности вычислим с помощью поверхностного интеграла по формуле:
![]()
В данном случае:
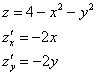
![]() – круг радиуса 2 с центром в начале координат.
– круг радиуса 2 с центром в начале координат.
Таким образом:
![]()
Осуществим переход к полярной системе координат:
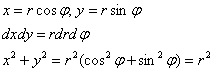
Порядок обхода области ![]() :
:
![]()
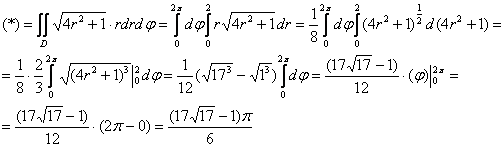
Ответ: ![]()
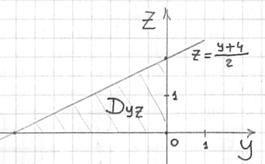
Пример 4. Решение: перепишем уравнение плоскости в отрезках:
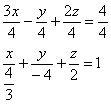
и выполним чертёж:
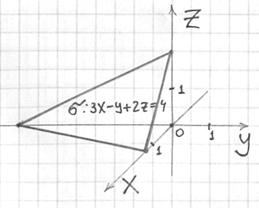
Поверхностный интеграл вычислим по формуле:
![]() , где
, где ![]() – проекция поверхности на плоскость
– проекция поверхности на плоскость ![]() .
.
В данном случае:
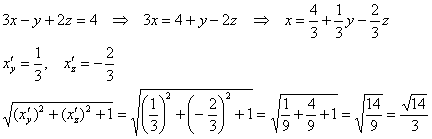
Таким образом:
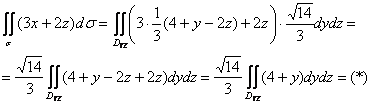
Найдём прямую ![]() и выполним чертёж области
и выполним чертёж области ![]() :
:
Выберем следующий порядок обхода:
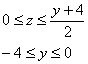
Таким образом:
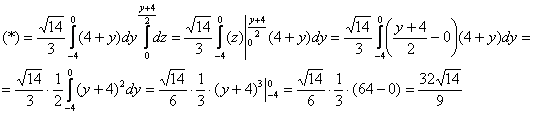
Ответ: 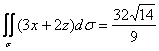
Пример 6. Решение: интеграл несколько проще вычислить первым способом. Выполним чертёж:
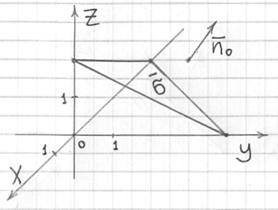
Так как единичный нормальный вектор поверхности ![]() образует с положительным направлением оси
образует с положительным направлением оси ![]() тупой угол, то используем формулу:
тупой угол, то используем формулу:
![]()
В данном случае:

Найдём линию пересечения плоскости ![]() с координатной плоскостью
с координатной плоскостью ![]() :
:
![]() и изобразим проекцию
и изобразим проекцию ![]() :
:
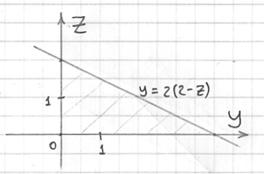
Выберем следующий порядок обхода области:
![]()
Таким образом:
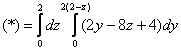
1) 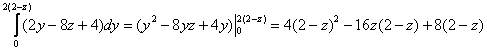
2)
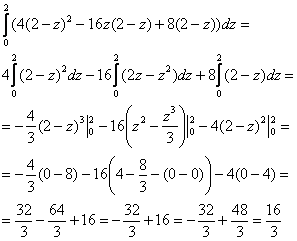
Ответ: ![]()
Второй способ решения можно найти здесь.
Пример 8. Решение: выполним чертёж:
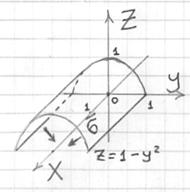
Способ первый:
![]()
1) Поскольку поверхность параллельна оси ![]() , то
, то ![]() ;
;
2) Интеграл ![]() разделим на две части. Векторы нормали к левой части поверхности
разделим на две части. Векторы нормали к левой части поверхности ![]() образуют с полуосью
образуют с полуосью ![]() острые углы, а к правой части поверхности
острые углы, а к правой части поверхности ![]() – тупые углы, поэтому:
– тупые углы, поэтому:
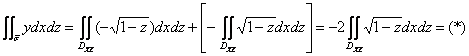
Изобразим область ![]() :
:
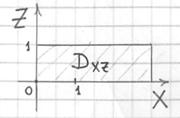

В результате: ![]()
Способ второй: сведём решении к поверхностному интегралу 1-го рода:
![]()
В данном случае: ![]()
Поскольку нормальные векторы внутренней стороны ![]() поверхности
поверхности ![]() образуют с полуосью
образуют с полуосью ![]() тупые углы, то функцию единичных векторов нормали составим по формуле:
тупые углы, то функцию единичных векторов нормали составим по формуле:
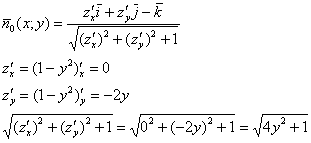
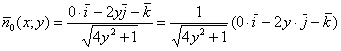
Вычислим скалярное произведение:
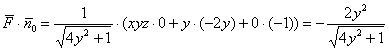
Таким образом:
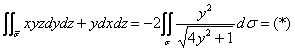
Используем формулу ![]()
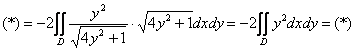
Изобразим область ![]() :
:
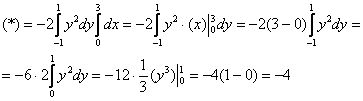
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
