
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Дифференциальные уравнения,
сводящиеся к однородным (и не только)
Этот небольшой практикум полезно проработать сразу после изучения вводной статьи о дифференциальных уравнениях и статьи об однородных ДУ. Несмотря на то, что указанный в заголовке тип уравнения довольно редко встречается на практике, сейчас вам представится отличная возможность отработать ОБЩУЮ ТЕХНИКУ решения диффуров, об азах и особенностях которой я рассказал на первом же уроке по теме. …Не будем тянуть кота за хвост, а потянем за дифференциальное уравнение вида:
![]() , где
, где ![]() – постоянные коэффициенты. При этом особой милости ждать не стОит – в большинстве практических примеров все или многие числа отличны от нуля. Более того, диффур может быть подзашифрован, например, так:
– постоянные коэффициенты. При этом особой милости ждать не стОит – в большинстве практических примеров все или многие числа отличны от нуля. Более того, диффур может быть подзашифрован, например, так:
![]()
Или так: ![]() плюс всякие «шероховатости» с раскрытием скобок и/или перестановкой слагаемых.
плюс всякие «шероховатости» с раскрытием скобок и/или перестановкой слагаемых.
Очевидно, что при ![]() уравнение является однородным, и сейчас нам предстоит разобраться в ситуации, когда хотя бы один из этих коэффициентов не равен нулю. Сия «неудобная» ситуация разрешима двумя путями…, …наверное, вы соскучились по высшей алгебре:
уравнение является однородным, и сейчас нам предстоит разобраться в ситуации, когда хотя бы один из этих коэффициентов не равен нулю. Сия «неудобная» ситуация разрешима двумя путями…, …наверное, вы соскучились по высшей алгебре:
– если определитель 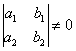 , то данное ДУ приводится к однородному уравнению, если же
, то данное ДУ приводится к однородному уравнению, если же 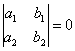 , то – к уравнению с разделяющимися переменными (либо переменные можно разделить сразу). Гораздо чаще приходится иметь дело с первым случаем, с него и начнём:
, то – к уравнению с разделяющимися переменными (либо переменные можно разделить сразу). Гораздо чаще приходится иметь дело с первым случаем, с него и начнём:
Пример 1
Решить дифференциальное уравнение ![]()
Решение: сначала проверяем, равен ли указанный выше определитель нулю: 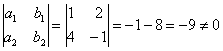 , значит, предложенное ДУ сводится именно к однородному уравнению.
, значит, предложенное ДУ сводится именно к однородному уравнению.
На первом шаге составим систему линейных уравнений с неизвестными «альфа» и «бета»:
![]()
По какому принципу составлена эта система, думаю, прекрасно видно. Так как вычисленный определитель системы отличен от нуля, то она имеет единственное решение:
![]()
Здесь я умножил 2-е уравнение на 2 и сложил уравнения почленно. Но, разумеется, можно использовать и любой другой способ решения, проще всего – «школьный».
Теперь в дифференциальном уравнении нужно провести следующие линейные замены:
![]() , где «икс и игрек с птичками» – новые переменные
, где «икс и игрек с птичками» – новые переменные
Обозначения, конечно, не сильно удобные, но другие варианты не особо лучше. Так, вместо ![]() иногда используют прописные буквы
иногда используют прописные буквы ![]() . Этот вариант, кстати, неплох, если вы оформляете решение в электронном виде, но в рукописи «большая» буква где-нибудь, да получится «малой». В некоторых источниках можно встретить переход к другим буквам, например, к паре
. Этот вариант, кстати, неплох, если вы оформляете решение в электронном виде, но в рукописи «большая» буква где-нибудь, да получится «малой». В некоторых источниках можно встретить переход к другим буквам, например, к паре ![]() . Однако в них точно запутаются «чайники». И поэтому давайте остановимся на «птичках», главное, следить, чтобы они «не улетели».
. Однако в них точно запутаются «чайники». И поэтому давайте остановимся на «птичках», главное, следить, чтобы они «не улетели».
Итак, в соответствии с обозначенными заменами, в уравнение ![]() ВМЕСТО «икса» подставляем
ВМЕСТО «икса» подставляем ![]() , а ВМЕСТО «игрека»
, а ВМЕСТО «игрека» ![]() :
:
![]()
Дифференциалы раскрываются «без последствий»:
![]()
и правая часть тоже в шоколаде:
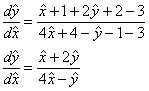
В результате свободные члены исчезли (как оно и должно было произойти), и мы имеем дело с банальным однородным уравнением, которое решается с помощью стандартной замены ![]() :
:
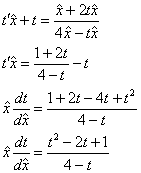
Разделяем переменные:
![]() и тут Внимание! Сбрасывая
и тут Внимание! Сбрасывая ![]() в знаменатель, мы рискуем потерять одно из решений, на чём я уже заострял внимание в статье об однородных уравнениях. Соотвествующую проверку выполним после нахождения общего интеграла:
в знаменатель, мы рискуем потерять одно из решений, на чём я уже заострял внимание в статье об однородных уравнениях. Соотвествующую проверку выполним после нахождения общего интеграла:
![]()
![]() – последние два шага сделаны для удобства последующего интегрирования.
– последние два шага сделаны для удобства последующего интегрирования.
В левой части можно использовать метод неопределённых коэффициентов, но рациональнее применить небольшой трюк, о котором я рассказывал ещё на уроке об интегрировании дробей:
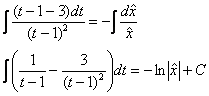
Обратите внимание, что константу не имеет никакого смысла «заталкивать» под логарифм – по той причине, что у нас нарисовались не только они:
![]()
Время собирать урожай! – упаковываем логарифмы:
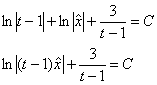
осуществляем обратную замену ![]() :
:
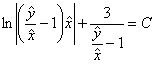
и АККУРАТНО проводим упрощения:
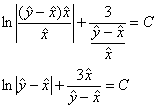
На завершающем этапе возвращаемся к исходным переменным:
![]() – и перед обратными заменами полезно просмотреть всё решение – не потеряли ли мы где-нибудь «птиц».
– и перед обратными заменами полезно просмотреть всё решение – не потеряли ли мы где-нибудь «птиц».
Опять же проявляем ПОВЫШЕННОЕ ВНИМАНИЕ:
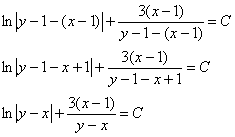
Напоминаю, что общий интеграл предпочтительнее записывать в виде ![]() .
.
Теперь вспоминаем о нашем неравносильном преобразовании (делении) и выясняем, является ли функция ![]() решением дифференциального уравнения. Используя обратную замену
решением дифференциального уравнения. Используя обратную замену ![]() , представляем эту функцию в явном виде:
, представляем эту функцию в явном виде:
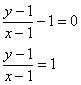
![]() – и подставляем её вместе со своей производной
– и подставляем её вместе со своей производной ![]() в исходное уравнение
в исходное уравнение ![]() :
:
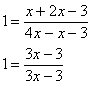
![]() – получено верное равенство, значит, функция
– получено верное равенство, значит, функция ![]() является решением данного ДУ, и, более того, она не учитывается в общем интеграле!
является решением данного ДУ, и, более того, она не учитывается в общем интеграле!
Таким образом, при делении на ![]() мы действительно потеряли решение, которое нужно дополнительно указать в ответе:
мы действительно потеряли решение, которое нужно дополнительно указать в ответе:
общий интеграл: ![]() , ещё одно решение:
, ещё одно решение: ![]()
Выполним проверку. Фактически она заключается в нахождении производной от неявно заданной функции:
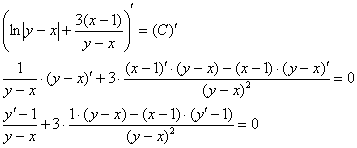
Приводим выражение левой части к общему знаменателю и избавляемся от дроби:
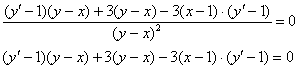
НЕ ТОРОПЯСЬ, проводим окончательные упрощения:
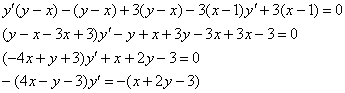
![]() – в результате получено исходное дифференциальное уравнение, значит, решение найдено верно.
– в результате получено исходное дифференциальное уравнение, значит, решение найдено верно.
Это была далеко не самая трудная проверка. По возможности, всегда старайтесь проверять полученный результат!
А теперь выполним задание, которое я обещал разобрать в статье об однородных уравнениях, а именно решим задачу Коши для такого уравнения. Найдём частное решение, удовлетворяющее, например, начальному условию ![]() . Как это сделать? Очень просто: в общий интеграл
. Как это сделать? Очень просто: в общий интеграл ![]() нужно подставить
нужно подставить ![]() и выяснить, чему равна константа:
и выяснить, чему равна константа:
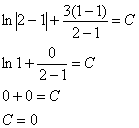
Таким образом, частный интеграл:
![]()
Мысленно убедитесь, что он удовлетворяет начальному условию ![]()
Пара интересных задач для самостоятельного решения:
Пример 2
Найти общее решение уравнения ![]()
Это задание примечательно тем, что «игрек» в нём остаётся «игреком» ;-)
Пример 3
Найти частное решение уравнения ![]() , соответствующее начальному условию
, соответствующее начальному условию ![]()
А здесь... впрочем, сами оцЕните! И узнаете нечто новое. Да, чуть не забыл – перед тем, как решать, приведите уравнение к виду ![]() – так будет гораздо удобнее.
– так будет гораздо удобнее.
Краткие решения и ответы в конце урока. Не ленимся выполнять проверку! – дифференцирования много не бывает =)
Систематизируем алгоритм решения уравнения ![]() (хотя бы один из коэффициентов
(хотя бы один из коэффициентов ![]() не равен нулю) для случая
не равен нулю) для случая 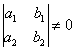 :
:
– Собственно, проверяем условие 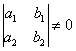 и делаем вывод, что уравнение сводится к однородному. Этот пункт можно выполнить и устно, ограничившись записью «сведём уравнение к однородному».
и делаем вывод, что уравнение сводится к однородному. Этот пункт можно выполнить и устно, ограничившись записью «сведём уравнение к однородному».
– Составляем и решаем систему 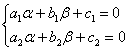
– Переходим к новым переменным ![]() . «Птички» можно заменить другими подходящими пометками, например, «волнами»:
. «Птички» можно заменить другими подходящими пометками, например, «волнами»: ![]() , или же вообще использовать другие буквы – кому как удобнее. Если
, или же вообще использовать другие буквы – кому как удобнее. Если ![]() или
или ![]() , то проводим только одну замену (ну а зачем «вхолостую» менять букву?).
, то проводим только одну замену (ну а зачем «вхолостую» менять букву?).
– В результате проведённых замен должно получиться однородное уравнение, которое решается по обычному алгоритму.
– Проводим обратные замены ![]() и приходим к общему интегралу. На завершающем этапе обязательно проверяем, не потеряли ли мы корни! Это может произойти в результате деления или сокращения на какую-либо отличную от константы функцию (например, когда мы сокращаем каждое слагаемое на
и приходим к общему интегралу. На завершающем этапе обязательно проверяем, не потеряли ли мы корни! Это может произойти в результате деления или сокращения на какую-либо отличную от константы функцию (например, когда мы сокращаем каждое слагаемое на ![]() ).
).
Для случая же 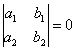 всё ещё проще. Здесь мы либо сразу разделяем переменные, либо добиваемся этой возможности с помощью одной из следующих замен:
всё ещё проще. Здесь мы либо сразу разделяем переменные, либо добиваемся этой возможности с помощью одной из следующих замен:
![]()
Сначала разберём частную версию уравнения ![]() в которой
в которой ![]() :
:
Пример 4
Решить уравнение ![]()
Решение: совершенно понятно, что 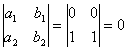 , и альтернативы нет – проводим замену:
, и альтернативы нет – проводим замену: ![]()
Находим дифференциал: ![]() , откуда выражаем
, откуда выражаем ![]() .
.
Теперь подставляем ![]() и
и ![]() в исходное уравнение:
в исходное уравнение:
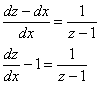
Дальнейшее просто:
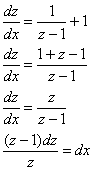
Внимание! Здесь мы сбросили «зет» в знаменатель, и к этому неравносильному преобразованию нужно будет вернуться в конце решения:
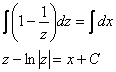
Обратная замена ![]() :
:
![]()
Теперь проверим, не является ли потерянная функция ![]() решением ДУ. Для этого подставляем её вместе со своей производной
решением ДУ. Для этого подставляем её вместе со своей производной ![]() в исходный диффур
в исходный диффур ![]() :
:
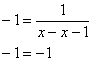
Является! И она не входит в общий интеграл ни при каком значении константы!
Ответ: общий интеграл: ![]() , ещё одно решение:
, ещё одно решение: ![]()
Проверка:
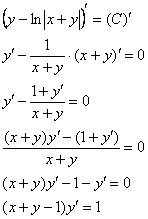
![]() , что и требовалось проверить.
, что и требовалось проверить.
Казалось бы, такое простенькое уравнение, но если не знать метод решения – придётся туго!
Вторая частная разновидность ![]() решается с помощью замены
решается с помощью замены ![]() . В силу линейности дифференциала:
. В силу линейности дифференциала: ![]() , откуда выражаем:
, откуда выражаем:
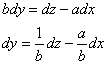
После чего подставляем ![]() и
и ![]() в наше уравнение:
в наше уравнение:
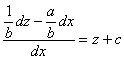
![]() – и всё дело тоже свелось к уравнению с разделяющимися переменными.
– и всё дело тоже свелось к уравнению с разделяющимися переменными.
Следует отметить, что уравнение ![]() является линейным неоднородным:
является линейным неоднородным:
![]() (стандартный вид), и к нему применимы обычные алгоритмы решения этого уравнения (см. по ссылке). Но, как вариант, годится и рассмотренная выше замена.
(стандартный вид), и к нему применимы обычные алгоритмы решения этого уравнения (см. по ссылке). Но, как вариант, годится и рассмотренная выше замена.
Уравнение с «полным комплектом» для самостоятельного изучения:
Пример 5
Найти общий интеграл уравнения
![]()
Подумайте, что лучше обозначить за «зет», впрочем, чего тут думать…. Для разнообразия я провёл решение через дифференциалы, но здесь, конечно, проще привести уравнение к «дробному» виду.
И в заключение урока хочу рассказать поучительную историю о том, почему же всё-таки не нужно тянуть котов за хвосты =) После написания 1-го абзаца статьи меня вдруг заинтересовало происхождение этого фразеологизма. И шустрый Гугл сразу же стал предлагать тематичную рекламу, которую я просто не мог не заскриншотить:

Но это было ещё не всё – в наше время успешен тот, кто учитывает интересы всех клиентов:

Честное слово, не Фотошоп!
И поэтому я рекомендую вам безотлагательно перейти к изучению линейных неоднородных уравнений 1-го порядка – чтобы на китайской барахолке появились и они! =)
Решения и ответы:
Пример 2. Решение: очевидно, что ![]() является решением данного уравнения. Вычислим:
является решением данного уравнения. Вычислим:
![]() , значит, данное уравнение приводится к однородному. Составим и решим систему:
, значит, данное уравнение приводится к однородному. Составим и решим систему:
![]()
Проведём замену ![]() :
:
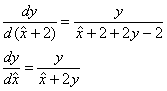
В полученном однородном уравнении проведём замену ![]() :
:
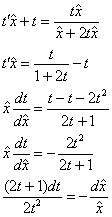
! Примечание: при делении на ![]() мы как раз и теряем «очевидное» решение
мы как раз и теряем «очевидное» решение ![]()
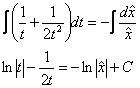
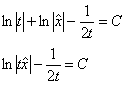
Обратная замена ![]() :
:
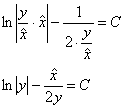
Обратная замена ![]()
Ответ: общий интеграл: ![]() , ещё одно решение:
, ещё одно решение: ![]() (которое не вошло в общий интеграл)
(которое не вошло в общий интеграл)
Пример 3. Решение: представим уравнение в виде ![]() и сведём его однородному. Составим и решим систему:
и сведём его однородному. Составим и решим систему:
![]()
Проведём замены ![]() :
:
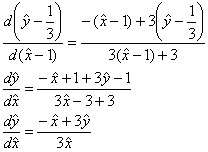
В полученном однородном уравнении проведём замену ![]() :
:
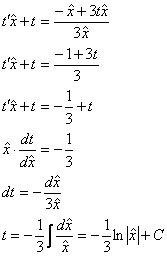
Обратная замена ![]() :
:
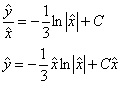
Обратные замены ![]() :
:
![]()
Общее решение: ![]()
Найдём частное решение, удовлетворяющее начальному условию ![]() :
:
![]()
Ответ: частное решение: ![]()
Примечание 1: по условию требовалось решить задачу Коши, и поэтому я не контролировал потерю решений. Но здесь следует помнить, что нужно частное решение может оказаться и среди потерянных!
Примечание 2: данное уравнение является линейным неоднородным: ![]() (стандартный вид) и его можно решить другими способами.
(стандартный вид) и его можно решить другими способами.
Пример 5. Решение: ![]() – сведём данное ДУ к уравнению с разделяющимися переменными. Проведём замену:
– сведём данное ДУ к уравнению с разделяющимися переменными. Проведём замену:
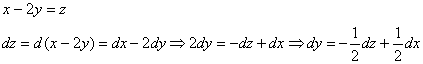
Выполним подстановки ![]() :
:
![]()
Умножим каждое слагаемое на –2:
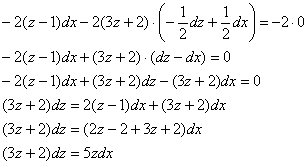
Разделяем переменные и интегрируем:
![]()
! Берём на заметку деление на «зет» и продолжаем:
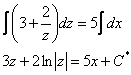
Обратная замена ![]() :
:
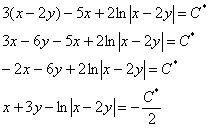
Поставим потерянную функцию ![]() и её дифференциал
и её дифференциал ![]() в исходное дифференциальное уравнение
в исходное дифференциальное уравнение ![]() :
:
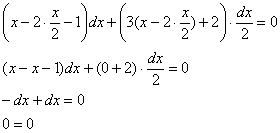
Таким образом, функция ![]() является корнем ДУ и не входит в общий интеграл. Переобозначим константу:
является корнем ДУ и не входит в общий интеграл. Переобозначим константу: ![]() и запишем окончательный
и запишем окончательный
ответ: общий интеграл: ![]() , ещё одно решение:
, ещё одно решение: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
