
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Циркуляция векторного поля. Формула Стокса
Заключительный урок по основам векторного анализа будет посвящён ещё одной характеристике векторного поля под названием циркуляция. С чем у нас ассоциируется этот термин на обывательском уровне? Циркуляция воздуха, циркуляция жидкости в некоторой системе; причём латинский корень данного слова (circulare) говорит нам, о том, что процесс идёт «по кругу».
Всё верно, понятие циркуляции пришло в теорию поля из гидродинамической задачи, где нужно было оценить движение жидкости по замкнутому контуру. Построим простейшую модель: пусть в некой замкнутой трубе циркулирует жидкость, и её движение описывается полем скоростей ![]() . Рассмотрим произвольную замкнутую линию тока
. Рассмотрим произвольную замкнутую линию тока ![]() . Упрощённо будем полагать, что каждой точке линии соответствует торчащий из неё вектор поля, который показывает направление и скорость движения жидкости в данной точке.
. Упрощённо будем полагать, что каждой точке линии соответствует торчащий из неё вектор поля, который показывает направление и скорость движения жидкости в данной точке.
Циркуляция (![]() ) векторного поля
) векторного поля ![]() по контуру
по контуру ![]() – это скалярная величина, численно равная криволинейному интегралу 2-го рода по этому контуру:
– это скалярная величина, численно равная криволинейному интегралу 2-го рода по этому контуру:
![]()
Согласно общему принципу интегрирования, данный интеграл объёдиняет проекции «торчащих» из контура векторов ![]() на координатные оси по всем бесконечно малым кусочкам
на координатные оси по всем бесконечно малым кусочкам ![]() контура, что и является оценкой движения жидкости. И непосредственно из интеграла видно, что циркуляция зависит от двух вещей:
контура, что и является оценкой движения жидкости. И непосредственно из интеграла видно, что циркуляция зависит от двух вещей:
– длины самого контура (чем длиннее, тем больше циркуляция);
– скорости течения * (чем длиннее векторы «эф», тем больше их бесконечно малые проекции и тем больше значение ![]() ).
).
* Со временем понятие циркуляции распространилось на произвольное векторное поле, где циркулировать в прямом смысле нечему
При этом контур, очевидно, можно обойти двумя способами: в одном направлении или в противоположном. В обоих случаях получится одно и то же абсолютное значение циркуляции с разными знаками (если, конечно, ![]() ). На практике чаще используется обход против часовой стрелки – когда для «идущего по контуру» человека ограниченная контуром область остаётся по левую руку. Такое направление обхода называют положительным.
). На практике чаще используется обход против часовой стрелки – когда для «идущего по контуру» человека ограниченная контуром область остаётся по левую руку. Такое направление обхода называют положительным.
Следует также заметить, что требование замкнутости контура не является обязательным – циркуляцию можно вычислить и по произвольной кусочно-гладкой линии, которая позволяет беспроблемно интегрировать. Однако исторически и методически сложилось так, что в практических задачах контур, как правило, замкнут.
И, если расписать криволинейный интеграл циркуляции для векторного поля ![]() подробно, то перед нами «откроется» её физический смысл:
подробно, то перед нами «откроется» её физический смысл:
![]()
А именно, циркуляция равна работе векторного поля по замкнутому контуру ![]() , о которой я, в том числе упоминал на первом уроке по теории поля. Этот смысл больше характерен для силовых полей, но и в гидродинамической модели результат можно интерпретировать как работу поля скоростей по перемещению материальной точки.
, о которой я, в том числе упоминал на первом уроке по теории поля. Этот смысл больше характерен для силовых полей, но и в гидродинамической модели результат можно интерпретировать как работу поля скоростей по перемещению материальной точки.
Таким образом, сегодня у нас будет две задачи «в одном флаконе»! К тому же криволинейных интегралов по пространственным контурам мы почти не решали, и сейчас самое время наверстать упущенное:
Пример 1
Вычислить циркуляцию векторного поля ![]() вдоль треугольника
вдоль треугольника ![]() в положительном направлении.
в положительном направлении.
![]()
Решение: изобразим треугольник ![]() на чертеже и обязательно пометим стрелочками порядок его обхода:
на чертеже и обязательно пометим стрелочками порядок его обхода:
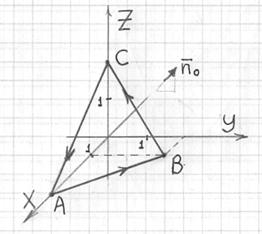
Циркуляция векторного поля по замкнутому контуру ![]() равна криволинейному интегралу 2-го рода по данному контуру, и в силу свойства аддитивности:
равна криволинейному интегралу 2-го рода по данному контуру, и в силу свойства аддитивности:
![]()
Как говорится, разделяй и властвуй:
1) Вычислим циркуляцию по отрезку ![]() :
:
![]()
По точкам ![]() и
и ![]() найдём направляющий вектор прямой
найдём направляющий вектор прямой ![]() :
:
![]() , и поскольку его «зетовая» координата равна нулю, то канонические уравнениЯ прямой принимают следующий вид:
, и поскольку его «зетовая» координата равна нулю, то канонические уравнениЯ прямой принимают следующий вид: ![]() . Мысленно проверяем, что координаты точек «а» и «бэ» удовлетворяют полученным уравнениям. Так как
. Мысленно проверяем, что координаты точек «а» и «бэ» удовлетворяют полученным уравнениям. Так как ![]() , то у нас есть возможность свести криволинейный интеграл к определённому интегралу с интегрированием по «икс» или по «игрек». Из левой пропорции выражаем:
, то у нас есть возможность свести криволинейный интеграл к определённому интегралу с интегрированием по «икс» или по «игрек». Из левой пропорции выражаем:
![]() и находим дифференциал:
и находим дифференциал: ![]() – таким образом решение сведётся к переменной «икс», которая в соответствии с направлением интегрирования изменяется (смотрим на чертёж!) от 3 до 1:
– таким образом решение сведётся к переменной «икс», которая в соответствии с направлением интегрирования изменяется (смотрим на чертёж!) от 3 до 1:
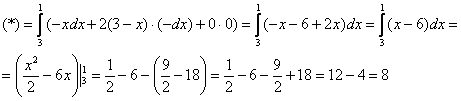
Как вариант, из уравнений прямой можно выразить ![]() , найти
, найти ![]() и проинтегрировать по «игрек» от 0 до 2. Не упускаем отличную возможность проверки:
и проинтегрировать по «игрек» от 0 до 2. Не упускаем отличную возможность проверки:
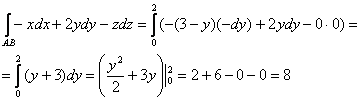
2) Вычислим циркуляцию векторного поля по отрезку ![]() :
:
![]()
Направляющий вектор соответствующей прямой найдём по точкам ![]() :
:
![]() – и поскольку все его координаты отличны от нуля, то нам не удастся «обнулить» какую-либо переменную в криволинейном интеграле. Что делать? Запишем параметрические уравнения прямой – по точке
– и поскольку все его координаты отличны от нуля, то нам не удастся «обнулить» какую-либо переменную в криволинейном интеграле. Что делать? Запишем параметрические уравнения прямой – по точке ![]() (удобнее взять начало пути) и направляющему вектору
(удобнее взять начало пути) и направляющему вектору ![]() :
:
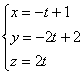
Нетрудно видеть, что началу ![]() отрезка соответствует значение
отрезка соответствует значение ![]() , а концу
, а концу ![]() – значение
– значение ![]() . Осталось найти дифференциалы параметрических уравнений:
. Осталось найти дифференциалы параметрических уравнений:
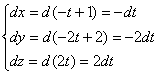
и АККУРАТНО подставить весь скарб:
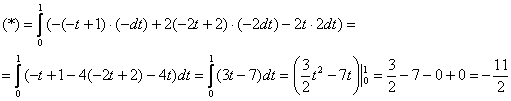
3) И, наконец, вычислим циркуляцию поля по отрезку ![]() :
:
![]()
Поскольку путь лежит в плоскости ![]() , то «игрековая» координата будет равна нулю, что позволяет нам свести решение к определённому интегралу по «икс» либо по «зет». Составим канонические уравнения прямой
, то «игрековая» координата будет равна нулю, что позволяет нам свести решение к определённому интегралу по «икс» либо по «зет». Составим канонические уравнения прямой ![]() по точке
по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]() – не забываем мысленно проверить, что координаты точек
– не забываем мысленно проверить, что координаты точек ![]() удовлетворяют полученным уравнениям.
удовлетворяют полученным уравнениям.
Из пропорции проще выразить ![]() , найти
, найти ![]() и проинтегрировать по «зет» (внимание!) от 2 до 0 – строго по направлению обхода:
и проинтегрировать по «зет» (внимание!) от 2 до 0 – строго по направлению обхода:
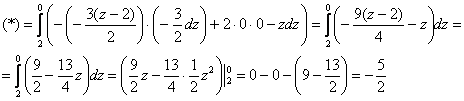
Не позволяй душе лениться – теперь выразим ![]() , найдём
, найдём ![]() и проинтегрируем по «икс» от 0 до 3:
и проинтегрируем по «икс» от 0 до 3:
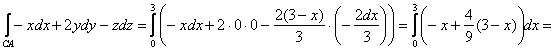
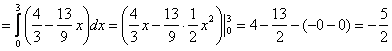 , что и требовалось проверить.
, что и требовалось проверить.
Кстати, и в первом, и в этом пункте можно использовать и параметрические уравнения – кому как удобнее.
Таким образом, циркуляция векторного поля по замкнутому контуру:
![]()
Ответ: ![]()
Скорее всего, вам не очень понятен этот результат с точки зрения гидродинамики, и чуть позже я объясню его смысл. Но прежде ответим на старый сакраментальный вопрос: а нельзя ли проще?
Формула Стокса
Циркуляция векторного поля ![]() по замкнутому контуру
по замкнутому контуру ![]() равна потоку его ротора через поверхность
равна потоку его ротора через поверхность ![]() , натянутую на данный контур в направлении, которое соответствует направлению обхода контура:
, натянутую на данный контур в направлении, которое соответствует направлению обхода контура:
![]()
а именно, если смотреть на поверхность из острия её нормальных векторов (вектора), то путь по контуру должен быть ВИДЕН НАМ, как осуществляемый ПРОТИВ часовой стрелки. Посмотрите на треугольник ![]() (чертёж выше) со стороны острия единичного нормального вектора
(чертёж выше) со стороны острия единичного нормального вектора ![]() . Обход контура осуществляется против часовой стрелки? Да*. Значит, это и есть нужный вектор нормали, и поэтому нам следует вычислить поверхностный интеграл по верхней стороне треугольника.
. Обход контура осуществляется против часовой стрелки? Да*. Значит, это и есть нужный вектор нормали, и поэтому нам следует вычислить поверхностный интеграл по верхней стороне треугольника.
* Посмотрите на ситуацию и с другой стороны треугольника
По формуле Стокса:
![]() , где
, где ![]() – единичный вектор нормали верхней стороны треугольника.
– единичный вектор нормали верхней стороны треугольника.
Примечание: по сути, в правой части записан поверхностный интеграл 2-го рода – уже сведённый к поверхностному интегралу 1-го рода
Найдём роторную функцию ![]() поля
поля ![]() . Чтобы не запутаться, выпишем компоненты поля, и возьмём частные производные в «роторном» порядке:
. Чтобы не запутаться, выпишем компоненты поля, и возьмём частные производные в «роторном» порядке:
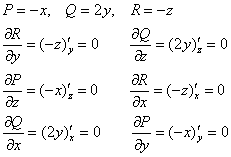
Таким образом:
![]() , следовательно, наше поле потенциально и:
, следовательно, наше поле потенциально и:
![]()
Ну ещё бы – если вспомнить физический смысл циркуляции (работа векторного поля по контуру), и вспомнить о том, что работа по замкнутому контуру в потенциальном поле равна нулю, то всё встаёт на свои места.
Таким образом, циркуляция векторного поля ![]() равна нулю не только по треугольнику
равна нулю не только по треугольнику ![]() , но и вообще по любому замкнутому контуру пространства. Из чего становится понятен и гидродинамический смысл задачи: представьте, что треугольник
, но и вообще по любому замкнутому контуру пространства. Из чего становится понятен и гидродинамический смысл задачи: представьте, что треугольник ![]() находится внутри замкнутой трубы. Поскольку поле скоростей потенциально, то циркуляция будет равна нулю не только по данному треугольнику, но и по любой внутренней замкнутой линии. Это говорит нам о том, что движение жидкости в трубе разнонаправлено и скомпенсировано – сколько циркулирует в одном направлении – столько проциркулирует и в другом.
находится внутри замкнутой трубы. Поскольку поле скоростей потенциально, то циркуляция будет равна нулю не только по данному треугольнику, но и по любой внутренней замкнутой линии. Это говорит нам о том, что движение жидкости в трубе разнонаправлено и скомпенсировано – сколько циркулирует в одном направлении – столько проциркулирует и в другом.
На самом деле формулой Стокса мы пользовались и раньше: если контур ![]() полностью лежит в плоскости
полностью лежит в плоскости ![]() , то получается её частный случай под названием формула Грина:
, то получается её частный случай под названием формула Грина:
![]() , где
, где ![]() – замкнутая область, ограниченная контуром
– замкнутая область, ограниченная контуром ![]() . И фактически сейчас мы прорешали пространственный аналог Примера 12 урока Криволинейные интегралы по замкнутому контуру.
. И фактически сейчас мы прорешали пространственный аналог Примера 12 урока Криволинейные интегралы по замкнутому контуру.
Интересно отметить, что рассмотренное в задаче поле является не только потенциальным, но ещё и соленоидальным:
![]()
Такие поля (одновременно потенциальные и соленоидальные) называют гармоническими. И под этот термин мне всегда представляется полноводная широкая река с ровным течением, по которой величественно, без малейшего отклонения от прямого курса плывёт разный мусор целая флотилия ладей. И в этом действительно есть какая-то завораживающая гармония. Однако, то лишь ассоциация – самостоятельно придумайте «бурный» пример ;)
В курсе векторного анализа существует целый раздел, посвящённый гармоническим полям, но сейчас мы возвращаемся к делам практическим, и для самостоятельного решения я предлагаю вам аналогичную задачу:
Пример 2
Вычислить циркуляцию векторного поля ![]() вдоль треугольника
вдоль треугольника ![]() в положительном направлении двумя способами: а) непосредственно, б) по формуле Стокса.
в положительном направлении двумя способами: а) непосредственно, б) по формуле Стокса.
![]()
Это более распространённый случай, где все отрезки лежат в координатных плоскостях, и поэтому здесь можно обойтись исключительно декартовыми координатами. Впрочем, параметрические уравнения тоже неплохой вариант, ибо буковка там всего одна =) – главное, правильно разобраться с пределами изменения параметра.
При использовании формулы Стокса не путаемся – в ней вычисляется поток НЕ САМОГО поля ![]() , а его ротора
, а его ротора ![]() . И да, тут потребуется составить уравнение плоскости.
. И да, тут потребуется составить уравнение плоскости.
НЕ ЛЕНИМСЯ и обязательно решаем это задание! Оно, может быть, не слишком интересно с точки зрения содержания, но крайне полезно для отработки техники решения криволинейных интегралов. В конце урока можно ознакомиться с образцом решения и некоторыми рациональными приёмами вычислений, позволяющими минимизировать трудозатраты и уменьшить риск ошибок.
Помимо контура-треугольника, пожалуй, популярнее только окружность:
Пример 3
Вычислить циркуляцию векторного поля ![]() вдоль замкнутого контура
вдоль замкнутого контура ![]() непосредственно и по формуле Стокса
непосредственно и по формуле Стокса
Решение: предложенные уравнения задают окружность, лежащую в плоскости ![]() , радиуса 2 с центром на оси
, радиуса 2 с центром на оси ![]() . Причём, в условии ничего не сказано о порядке обхода контура, и мы, в принципе, можем выбрать любой из них. Пойдём «традиционным» путём:
. Причём, в условии ничего не сказано о порядке обхода контура, и мы, в принципе, можем выбрать любой из них. Пойдём «традиционным» путём:
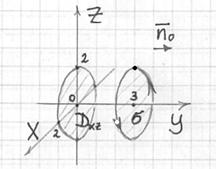
1) Вычислим работу векторного поля непосредственно. С «иксом», «игреком», «зет» и их дифференциалами тут всё прозрачно:
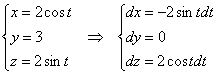
и осталось проконтролировать пределы изменения параметра:
– если ![]() , то
, то ![]() – белая точка контура (см. чертёж);
– белая точка контура (см. чертёж);
– если ![]() , то
, то ![]() – самая верхняя точка контура.
– самая верхняя точка контура.
Таким образом, при изменении ![]() окружность «прорисовывается» в противоположном направлении по отношению к нашему порядку обхода, и поэтому интеграл следует взять от
окружность «прорисовывается» в противоположном направлении по отношению к нашему порядку обхода, и поэтому интеграл следует взять от ![]() до 0:
до 0:
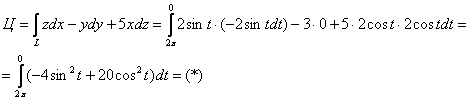
Используем тригонометрические формулы ![]() :
:
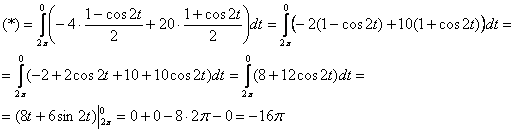
Ответ: ![]()
Отрицательный знак говорит нам о том, что циркуляция осуществляется (полностью или преимущественно) против выбранного нами порядка обхода, и если бы мы обошли окружность в противоположном направлении, то получилось бы ![]()
2) Вычислим циркуляцию по формуле Стокса:
![]()
Найдём роторную функцию:
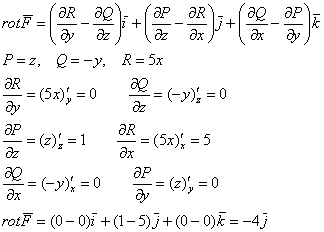
Поскольку поверхность ![]() , натянутая на контур
, натянутая на контур ![]() , представляет собой плоскую фигуру (круг), то для всех её точек единичный вектор нормали может «смотреть» лишь в две стороны. Какой вектор выбрать:
, представляет собой плоскую фигуру (круг), то для всех её точек единичный вектор нормали может «смотреть» лишь в две стороны. Какой вектор выбрать: ![]() или
или ![]() ? Вспоминаем правило: из острия вектора обход контура должен быть ВИДЕН НАМ против часовой стрелки. Этому условию удовлетворяет вектор
? Вспоминаем правило: из острия вектора обход контура должен быть ВИДЕН НАМ против часовой стрелки. Этому условию удовлетворяет вектор ![]() . Обязательно взгляните на круг и с другой стороны – с этой точки зрения контур обходится ПО часовой стрелке, и поэтому вектор
. Обязательно взгляните на круг и с другой стороны – с этой точки зрения контур обходится ПО часовой стрелке, и поэтому вектор ![]() не годится.
не годится.
Найдём скалярное произведение:
![]()
Теперь заряжаем формулу Стокса:
![]()
Здесь можно сослаться на то, что интеграл ![]() равен площади
равен площади ![]() -круга:
-круга: ![]() и сразу дать ответ
и сразу дать ответ ![]() , но мы пойдём академичным путём.
, но мы пойдём академичным путём.
Коль скоро, поверхность ![]() «полноценно» проецируется лишь на плоскость
«полноценно» проецируется лишь на плоскость ![]() , то ничего не остаётся, как применить частную формулу
, то ничего не остаётся, как применить частную формулу ![]() . Особо подчёркиваю, что это частный случай, и если бы под интегралом были хоть какие-то переменные, то потребовалась бы полная версия
. Особо подчёркиваю, что это частный случай, и если бы под интегралом были хоть какие-то переменные, то потребовалась бы полная версия ![]()
Но у нас всё проще: ![]()
![]()
И здесь снова можно сослаться, что полученный двойной интеграл численно равен площади круга ![]() такого же радиуса, но я таки «добью» интеграл с помощью «экзотического» перехода к полярным координатам в плоскости
такого же радиуса, но я таки «добью» интеграл с помощью «экзотического» перехода к полярным координатам в плоскости ![]() . С порядком обхода тут всё ясно:
. С порядком обхода тут всё ясно:
![]()
![]() – обратите внимание, что полярный угол изменяется в стандартном направлении, от полуоси
– обратите внимание, что полярный угол изменяется в стандартном направлении, от полуоси ![]() в сторону полуоси
в сторону полуоси ![]() . Грубо говоря, роль «игрека» здесь выполняет переменная «зет», а значит
. Грубо говоря, роль «игрека» здесь выполняет переменная «зет», а значит ![]() :
:
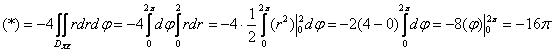
Ответ: ![]()
Если выбрать другое направление обхода окружности ![]() , то придётся использовать противоположно направленный вектор
, то придётся использовать противоположно направленный вектор ![]() , из-за чего, очевидно, сменится знак. Однако отрицательный знак ничем не хуже положительного и говорит лишь о том, что мы подсчитали циркуляцию полностью или преимущественно «против течения».
, из-за чего, очевидно, сменится знак. Однако отрицательный знак ничем не хуже положительного и говорит лишь о том, что мы подсчитали циркуляцию полностью или преимущественно «против течения».
Пара задач для самостоятельного решения. Попроще:
Пример 4
Вычислить циркуляцию векторного поля ![]() вдоль замкнутого контура
вдоль замкнутого контура ![]() непосредственно и по формуле Стокса. Выбрать положительное направление обхода.
непосредственно и по формуле Стокса. Выбрать положительное направление обхода.
В образце я привёл скрупулезное решение, но на практике можно пользоваться и геометрическим смыслом интегралов, обычно преподаватели к этому относятся лояльно.
И задачка позанятнее:
Пример 5
Найти модуль циркуляции векторного поля ![]() вдоль контура
вдоль контура 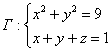
Контур здесь представляет собой линию пересечения цилиндра и плоскости, а именно, эллипс; и, кстати, на уроке о тройных интегралах в Примере 7 я рассказывал, как построить такое сечение. Интересно отметить, что тут можно легко обойтись без чертежа, поскольку требуется найти абсолютное значение циркуляции, то направление обхода не имеет значения – просто тупо интегрируем по «тэ» от 0 до ![]() . С параметрическими уравнениями «косого» эллипса, думаю проблем возникнуть не должно. Но, это палка о двух концах – возможно, вам покажется проще решение вторым способом.
. С параметрическими уравнениями «косого» эллипса, думаю проблем возникнуть не должно. Но, это палка о двух концах – возможно, вам покажется проще решение вторым способом.
Существует и более сложные задачи, однако в рамках данного урока этого будет достаточно, ибо лучше проще – да понятнее. Кроме того, я далеко не всё рассказал по теме, в частности о том, что само понятие ротора определяется через циркуляцию и поверхность, натянутую на контур + ещё один интересный момент, который касается поверхности. Читайте, например, 3-й том Фихтенгольца.
Ну а я поздравляю вас с успешным прохождением занимательного курса по теории поля. Надеюсь, он был понятен, интересен и полезен, и теперь никому не будут страшнЫ, по крайне мере, навороченные обозначения в учебниках.
Всё что осталось сделать – это вручить вам в руки лопату и отправить на обширное поле векторного анализа =) Дополнительные задачи с решениями есть в соответствующем архиве банка решений, библиотеке mathprofi.com, или в этом решебнике. Только будьте осторожны и критичны – недочёты и ошибки могут быть где угодно.
Желаю успехов!
Решения и ответы:
Пример 2: Решение: изобразим контур интегрирования на чертеже:
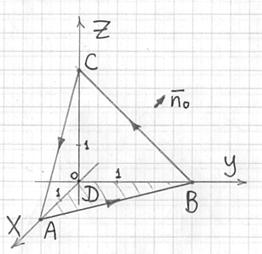
а) Решим задачу непосредственно:
![]()
1) Вычислим циркуляцию по отрезку ![]() . Так как
. Так как ![]() , то:
, то:
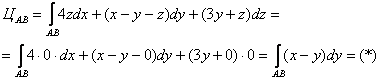
Составим уравнения прямой ![]() по точке
по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]() , откуда выразим:
, откуда выразим:
![]()
При этом ![]() изменяется от 0 до 3:
изменяется от 0 до 3:
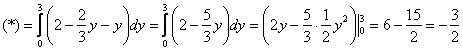
Проверьте решение другим способом!
2) Вычислим циркуляцию поля по отрезку ![]() . Так как
. Так как ![]() , то:
, то:
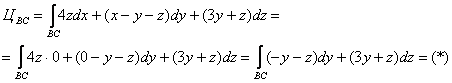
Составим уравнения прямой ![]() по точке
по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]() , откуда:
, откуда:
![]()
Найдём дифференциал: ![]()
![]() изменяется от 3 до 0:
изменяется от 3 до 0:
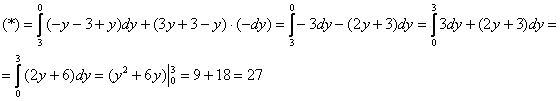
Самостоятельно проведите решение по переменной «зет»
3) Вычислим циркуляцию поля по отрезку ![]() . Так как
. Так как ![]() , то:
, то:
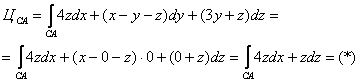
Составим уравнения прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]()
В данном случае выгоднее выразить ![]()
![]() изменяется от 3 до 0:
изменяется от 3 до 0:
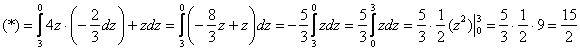
Таким образом, циркуляция по замкнутому контуру:
![]()
Ответ: ![]()
б) Вычислим циркуляцию векторного поля по формуле Стокса:
![]()
Найдём ротор векторного поля:
![]() . В данном случае:
. В данном случае:
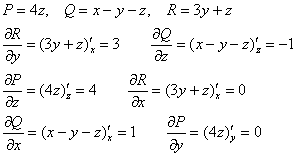
Таким образом:
![]()
Составим уравнение плоскости ![]() по точке
по точке ![]() и векторам
и векторам ![]() :
:
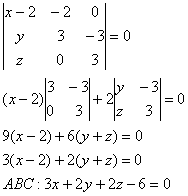
Запишем вектор нормали этой плоскости: ![]() и найдём соответствующий единичный вектор:
и найдём соответствующий единичный вектор:
![]()
Примечание: из острия данного вектора обход контур виден нам против часовой стрелки, следовательно, это и есть нужный вектор нормали
Найдём скалярное произведение:
![]()
Таким образом: ![]()
Для вычисления поверхностного интеграла 1-го рода используем формулу ![]() , где
, где ![]() – проекция треугольника
– проекция треугольника ![]() на плоскость
на плоскость ![]() .
.
В данном случае:
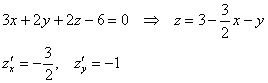

Двойной интеграл ![]() численно равен площади треугольника
численно равен площади треугольника ![]() :
:
![]()
Ответ: ![]()
Пример 4: Решение: выполним чертёж:
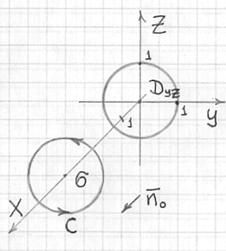
1) Вычислим работу векторного поля непосредственно:
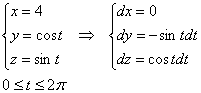
Таким образом:
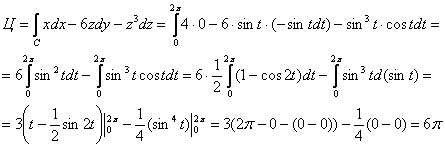
2) Вычислим циркуляцию по формуле Стокса:
![]() , где
, где ![]() – поверхность, натянутая на контур
– поверхность, натянутая на контур ![]()
Найдём ![]() . В данном случае:
. В данном случае:
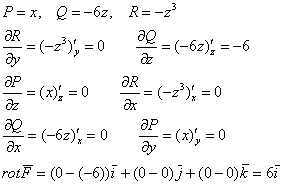
Скалярное произведение:
![]()
Таким образом:
![]()
Спроецируем поверхность ![]() на плоскость
на плоскость ![]() и воспользуемся формулой
и воспользуемся формулой
![]() , где
, где ![]() – проекция поверхности
– проекция поверхности ![]() . В данном случае
. В данном случае ![]() :
:
![]()
Перейдем к полярным координатам в плоскости ![]() :
:
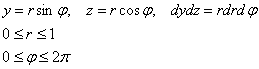
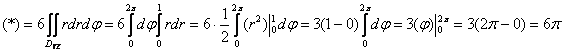
Ответ: ![]()
Пример 5: Решение: запишем параметрические уравнения цилиндра:
![]() (любое действительное число)
(любое действительное число)
Подставим первые два уравнения в уравнение плоскости:
![]()
Таким образом, сечение цилиндра плоскостью (эллипс) определяется уравнениями:
![]()
Найдём дифференциалы:
![]()
и вычислим циркуляцию векторного поля по контуру Г в направлении, которое соответствует изменению параметра в пределах ![]() :
:
 Выполнять упрощения и считать интегралы, конечно же, удобнее по отдельности =)
Выполнять упрощения и считать интегралы, конечно же, удобнее по отдельности =)
Ответ: ![]()
Постарайтесь прийти к этому же результату, используя формулу Стокса.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
