
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Асимптоты графика функции
Призрак асимптоты давно бродил по сайту чтобы, наконец, материализоваться в отдельно взятой статье и привести в особый восторг читателей, озадаченных полным исследованием функции. Нахождение асимптот графика – одна из немногих частей указанного задания, которая освещается в школьном курсе лишь в обзорном порядке, поскольку события вращаются вокруг вычисления пределов функций, а они относятся всё-таки к высшей математике. Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен ;-) …стоп-стоп, вы куда? Пределы – это легко!
Примеры асимптот встретились сразу же на первом уроке о графиках элементарных функций, и сейчас тема получает детальное рассмотрение.
Итак, что такое асимптота?
Представьте переменную точку, которая «ездит» по графику функции. Асимптота – это прямая, к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.
Примечание: определение содержательно, если вам необходима формулировка в обозначениях математического анализа, пожалуйста, обратитесь к учебнику.
На плоскости асимптоты классифицируют по их естественному расположению:
1) Вертикальные асимптоты, которые задаются уравнением вида ![]() , где «альфа» – действительное число. Популярная представительница
, где «альфа» – действительное число. Популярная представительница ![]() определяет саму ось ординат,
определяет саму ось ординат, с приступом лёгкой тошноты вспоминаем гиперболу ![]() .
.
2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом ![]() . Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты
. Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты ![]() . Например, та же гипербола с асимптотой
. Например, та же гипербола с асимптотой ![]() .
.
Резво пошло-поехало, ударим по теме короткой автоматной очередью:
Сколько асимптот может быть у графика функции?
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.
Вертикальные асимптоты графика функции
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке ![]() функция
функция ![]() терпит бесконечный разрыв, то прямая, заданная уравнением
терпит бесконечный разрыв, то прямая, заданная уравнением ![]() является вертикальной асимптотой графика.
является вертикальной асимптотой графика.
Примечание: обратите внимание, что запись ![]() используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой – зависит от контекста.
используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой – зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты ![]() в точке
в точке ![]() достаточно показать, что хотя бы один из односторонних пределов
достаточно показать, что хотя бы один из односторонних пределов ![]() бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация:
бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: ![]() и ось ординат (см. Графики и свойства элементарных функций).
и ось ординат (см. Графики и свойства элементарных функций).
Из вышесказанного также следует очевидный факт: если функция непрерывна на ![]() , то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция ![]() не определена на всей числовой прямой, однако совершенно обделена асимптотами.
не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше двух наклонных асимптот. Например, график экспоненциальной функции ![]() обладает единственной горизонтальной асимптотой при
обладает единственной горизонтальной асимптотой при ![]() , а график арктангенса
, а график арктангенса ![]() при
при ![]() – двумя такими асимптотами, причём различными.
– двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью ![]() . Например, …правильно догадались:
. Например, …правильно догадались: ![]() .
.
Общее практическое правило:
Если существуют два конечных предела ![]() , то прямая
, то прямая ![]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![]() при
при ![]() . Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
. Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
Примечание: формулы остаются справедливыми, если «икс» стремится только к «плюс бесконечности» или только к «минус бесконечности».
Покажем, что у параболы ![]() нет наклонных асимптот:
нет наклонных асимптот:
![]()
Предел бесконечен, значит, наклонная асимптота отсутствует. Заметьте, что в нахождении предела ![]() необходимость отпала, поскольку ответ уже получен.
необходимость отпала, поскольку ответ уже получен.
Примечание: если у вас возникли (или возникнут) трудности с пониманием знаков «плюс-минус», «минус-плюс», пожалуйста, посмотрите справку в начале урока
о бесконечно малых функциях, где я рассказал, как правильно интерпретировать данные знаки.
Очевидно, что у любой квадратичной, кубической функции, многочлена 4-й и высших степеней также нет наклонных асимптот.
А теперь убедимся, что при ![]() у графика
у графика ![]() тоже нет наклонной асимптоты. Для раскрытия неопределённости используем правило Лопиталя:
тоже нет наклонной асимптоты. Для раскрытия неопределённости используем правило Лопиталя:
![]() , что и требовалось проверить.
, что и требовалось проверить.
При ![]() функция
функция ![]() неограниченно растёт, однако не существует такой прямой, к которой бы её график приближался бесконечно близко.
неограниченно растёт, однако не существует такой прямой, к которой бы её график приближался бесконечно близко.
Переходим к практической части урока:
Как найти асимптоты графика функции?
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться). Начнём с чего-нибудь простого:
Пример 1
Найти асимптоты графика функции
![]()
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при ![]() , и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением
, и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением ![]() , является вертикальной асимптотой графика функции
, является вертикальной асимптотой графика функции ![]() . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
. Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
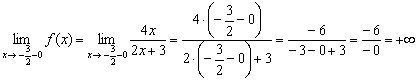
Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва. В выражение под знаком предела вместо «икса» подставляем ![]() . В числителе ничего интересного:
. В числителе ничего интересного:
![]() .
.
А вот в знаменателе получается бесконечно малое отрицательное число:
![]() , оно и определяет судьбу предела.
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО. Поэтому обязательно вычислим и правосторонний предел:
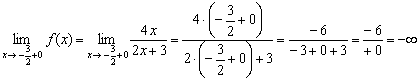
Вывод: односторонние пределы бесконечны, значит, прямая ![]() является вертикальной асимптотой графика функции при
является вертикальной асимптотой графика функции при ![]() .
.
2) Проверим наличие наклонных асимптот:
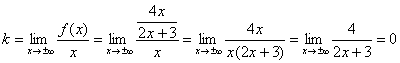
Первый предел конечен, значит, необходимо «продолжить разговор» и найти второй предел:
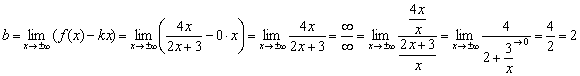
Второй предел тоже конечен.
Таким образом, наша асимптота:
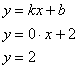
Вывод: прямая, заданная уравнением ![]() является горизонтальной асимптотой графика функции при
является горизонтальной асимптотой графика функции при ![]() .
.
Для нахождения горизонтальной асимптоты
можно пользоваться упрощенной формулой:
Если существует конечный предел ![]() , то прямая
, то прямая ![]() является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции ![]() при
при ![]() .
.
Нетрудно заметить, что числитель и знаменатель функции ![]() одного порядка роста, а значит, искомый предел будет конечным:
одного порядка роста, а значит, искомый предел будет конечным:
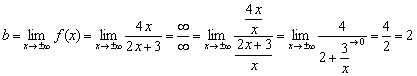
Ответ: ![]()
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции, то на черновике сразу же делаем набросок:
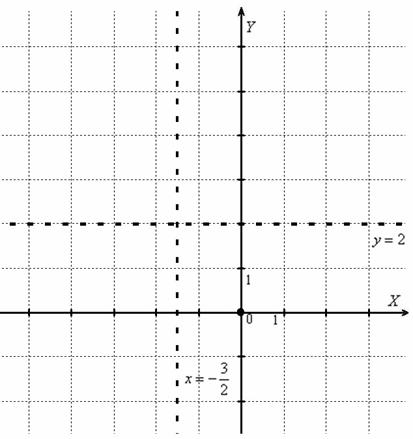
Исходя из трёх найденных пределов ![]() , попытайтесь самостоятельно прикинуть, как может располагаться график функции
, попытайтесь самостоятельно прикинуть, как может располагаться график функции ![]() . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
. Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
![]()
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдена по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
![]()
Решение: Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение:
![]()
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
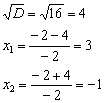
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители:
![]() (для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде ![]()
Найдём односторонние пределы в точке ![]() :
:
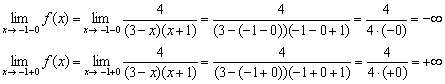
И в точке ![]() :
:
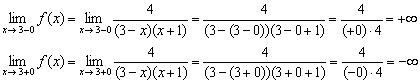
Таким образом, прямые ![]() являются вертикальными асимптотами графика рассматриваемой функции.
являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию ![]() , то совершенно очевидно, что предел
, то совершенно очевидно, что предел ![]() будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
![]()
Таким образом, прямая ![]() (ось абсцисс) является горизонтальной асимптотой графика данной функции.
(ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ: ![]()
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
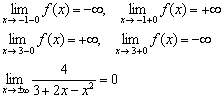
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции. Правильная картинка – в конце урока.
Пример 4
Найти асимптоты графика функции
![]()
Пример 5
Найти асимптоты графика функции
![]()
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше, чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста. В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая – через предел ![]() .
.
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
![]()
Решение: классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт № 1 закрыт.
2) Проверим наличие наклонных асимптот:
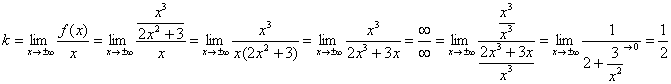
Первый предел конечен, поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:
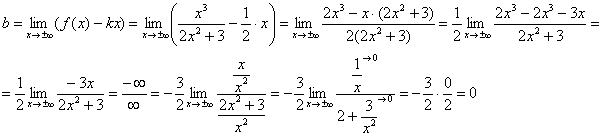
Второй предел тоже конечен, следовательно, у графика рассматриваемой функции существует наклонная асимптота:
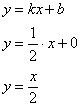
Вывод: ![]()
Таким образом, при ![]() график функции
график функции ![]() бесконечно близко приближается к прямой
бесконечно близко приближается к прямой ![]() :
:
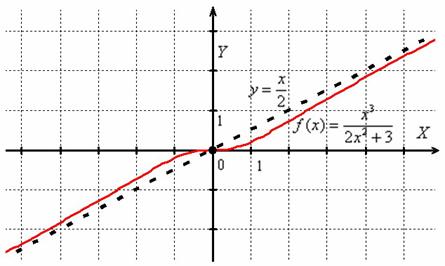
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
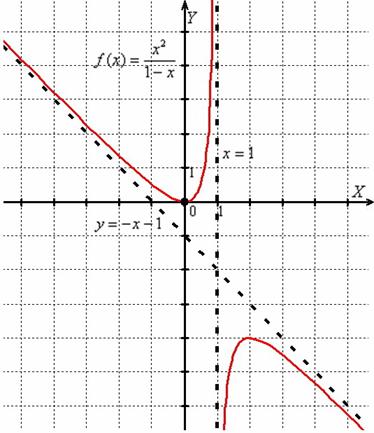
Пример 7
Найти асимптоты графика функции
![]()
Решение: комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку ![]() .
.
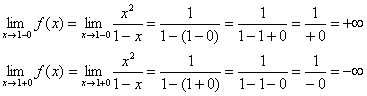
Прямая ![]() является вертикальной асимптотой для графика
является вертикальной асимптотой для графика ![]() при
при ![]() .
.
2) Наклонные асимптоты:
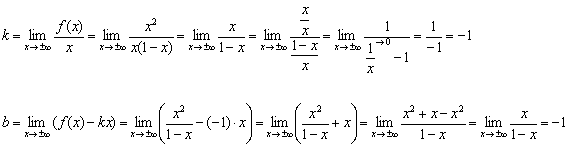
Прямая ![]() является наклонной асимптотой для графика
является наклонной асимптотой для графика ![]() при
при ![]() .
.
Ответ: ![]()
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
![]()
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше – наклонной асимптоты уже не будет (например, ![]() ).
).
Но в жизни происходят и другие чудеса:
Пример 9
Исследовать график функции на наличие асимптот
![]()
Решение: функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствует. Но вот наклонные вполне могут быть. Проверяем:
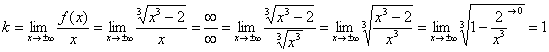
Вспоминаю, как ещё в ВУЗе столкнулся с похожей функцией и просто не мог поверить, что у неё есть наклонная асимптота. До тех пор, пока не вычислил второй предел:
![]()
Строго говоря, здесь две неопределённости: ![]() и
и ![]() , но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности. Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой
, но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности. Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой ![]() :
:
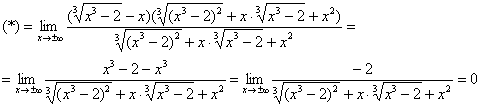
Ответ: ![]()
Пожалуй, самая популярная наклонная асимптота.
До сих пор бесконечности удавалось «стричь под одну гребёнку», но бывает, что у графика функции две разные наклонные асимптоты при ![]() и при
и при ![]() :
:
Пример 10
Исследовать график функции на наличие асимптот
![]()
Решение: подкоренное выражение положительно, значит, область определения – любое действительно число, и вертикальных палок быть не может.
Проверим, существуют ли наклонные асимптоты.
Если «икс» стремится к «минус бесконечности», то: 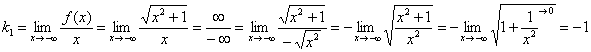
(при внесении «икса» под квадратный корень необходимо добавить знак «минус», чтобы не потерять отрицательность знаменателя)
![]()
Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:
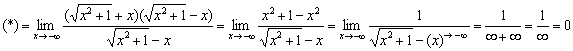
Таким образом, прямая ![]() является наклонной асимптотой графика при
является наклонной асимптотой графика при ![]() .
.
С «плюс бесконечностью» всё тривиальнее:
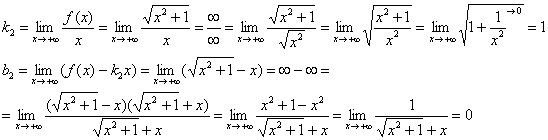
А прямая ![]() – при
– при ![]() .
.
Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Не удержусь от графического изображения:
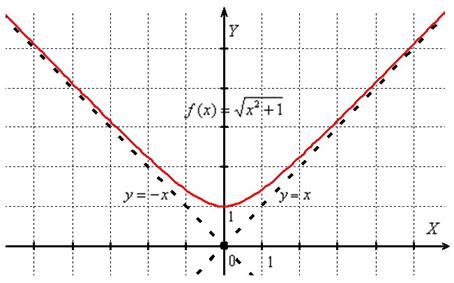
Это одна из ветвей гиперболы ![]() .
.
Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции:
Пример 11
Исследовать график функции на наличие асимптот
![]()
Решение: очевидно, что ![]() , поэтому рассматриваем только правую полуплоскость, где есть график функции.
, поэтому рассматриваем только правую полуплоскость, где есть график функции.
1) Функция непрерывна на интервале ![]() , а значит, если вертикальная асимптота и существует, то это может быть только ось ординат. Исследуем поведение функции вблизи точки
, а значит, если вертикальная асимптота и существует, то это может быть только ось ординат. Исследуем поведение функции вблизи точки ![]() справа:
справа:
![]()
Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов).
Таким образом, прямая ![]() (ось ординат) является вертикальной асимптотой для графика функции
(ось ординат) является вертикальной асимптотой для графика функции ![]() при
при ![]() .
.
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопиталя мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: ![]() (см. Пример 1 того же урока).
(см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при ![]() .
.
Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Чертёж для наглядности:
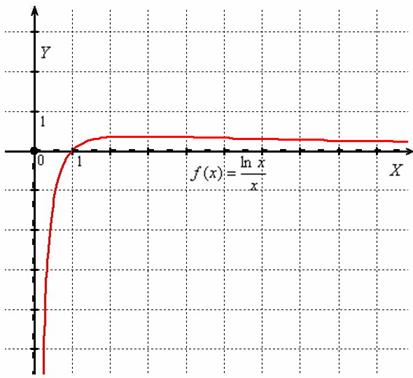
Интересно, что у вроде бы похожей функции ![]() асимптот нет вообще (желающие могут это проверить).
асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
![]()
Для проверки на вертикальные асимптоты сначала нужно найти область определения функции, а затем вычислить пару односторонних пределов в «подозрительных» точках. Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Пример 13
Исследовать график функции на наличие асимптот
![]()
А здесь могут быть только наклонные асимптоты, причём направления ![]() ,
, ![]() следует рассмотреть отдельно.
следует рассмотреть отдельно.
Надеюсь, вы отыскали нужную асимптоту =)
Желаю успехов!
Решения и ответы:
Пример 2: Решение:
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке ![]() . Найдём односторонние пределы:
. Найдём односторонние пределы:
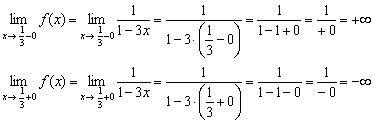
Прямая ![]() является вертикальной асимптотой графика функции при
является вертикальной асимптотой графика функции при ![]() .
.
2) Наклонные асимптоты.
![]()
Прямая ![]() (ось абсцисс) является горизонтальной асимптотой графика функции при
(ось абсцисс) является горизонтальной асимптотой графика функции при ![]() .
.
Ответ: ![]()
Чертёж к Примеру 3:
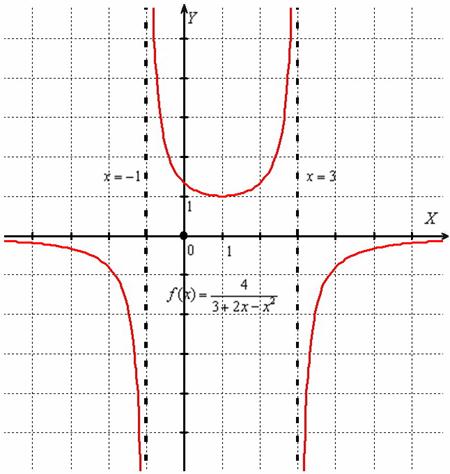
Пример 4: Решение:
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке ![]() . Вычислим односторонние пределы:
. Вычислим односторонние пределы:
![]()
Примечание: бесконечно малое отрицательное число в чётной степени равно бесконечно малому положительному числу: ![]() .
.
![]()
Прямая ![]() является вертикальной асимптотой графика функции.
является вертикальной асимптотой графика функции.
2) Наклонные асимптоты.
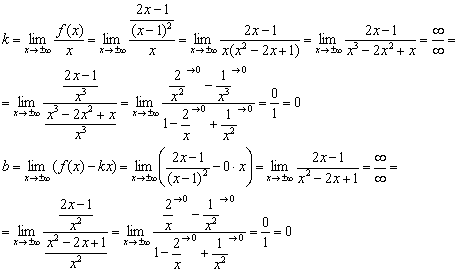
Прямая ![]() (ось абсцисс) является горизонтальной асимптотой графика функции при
(ось абсцисс) является горизонтальной асимптотой графика функции при ![]() .
.
Ответ: ![]()
Пример 5: Решение:
1) Исследуем функцию на наличие вертикальных асимптот. Найдём точки, в которых знаменатель обращается в ноль:
![]()
Действительных корней нет.
Исследуемая функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствуют.
2) Наклонные асимптоты.
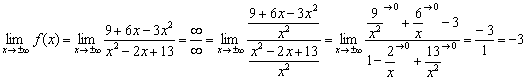
Прямая ![]() является горизонтальной асимптотой графика функции при
является горизонтальной асимптотой графика функции при ![]() .
.
Ответ: ![]()
Чертёж к Примеру 7:
Пример 8: Решение:
1) Вертикальные асимптоты. Исследуем точку ![]() .
.
![]() ,
,
Примечание: бесконечно малое отрицательное число в нечётной степени равно бесконечно малому отрицательному числу: ![]() .
.
![]() .
.
Прямая ![]() (ось
(ось ![]() ) является вертикальной асимптотой для графика
) является вертикальной асимптотой для графика ![]() , если
, если ![]() .
.
2) Наклонные асимптоты:
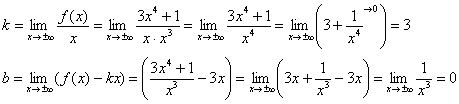
Прямая ![]() является наклонной асимптотой для графика
является наклонной асимптотой для графика ![]() при
при ![]() .
.
Ответ: ![]()
График данной функции:
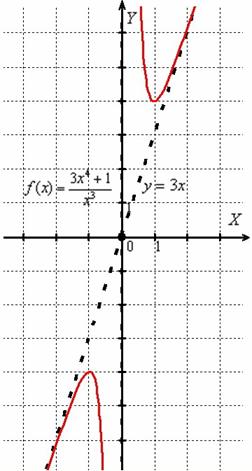
Пример 12: Решение: найдём область определения функции:
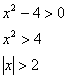
![]() .
.
Помимо аналитического способа нахождения области определения можно использовать и метод интервалов.
1) Проверим наличие вертикальных асимптот. Для удобства и наглядности вычислений разложим аргумент логарифма на множители:
![]()
Вычислим односторонние пределы:
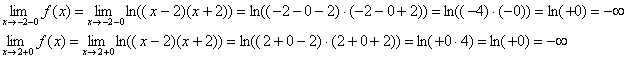 Таким образом, прямые
Таким образом, прямые ![]() являются вертикальными асимптотами для графика функции при
являются вертикальными асимптотами для графика функции при ![]() и
и ![]() соответственно.
соответственно.
2) Наклонные асимптоты.
Дважды используем правило Лопиталя:
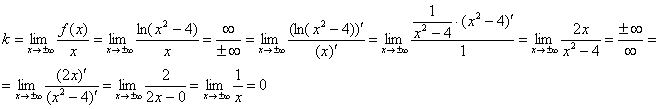 Первый предел конечен, находим второй предел:
Первый предел конечен, находим второй предел:
![]()
Значит, наклонные асимптоты отсутствуют.
Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Пример 13: Решение: так как функция непрерывна на ![]() , то вертикальные асимптоты отсутствуют.
, то вертикальные асимптоты отсутствуют.
Выясним, есть ли у графика наклонные асимптоты:
![]()
Значит, при ![]() у графика нет наклонной асимптоты.
у графика нет наклонной асимптоты.
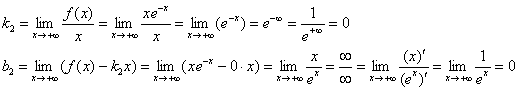
Таким образом, прямая ![]() является горизонтальной асимптотой графика данной функции при
является горизонтальной асимптотой графика данной функции при ![]() .
.
Ответ: ось абсцисс при ![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
