
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Ряды Фурье. Примеры решений
До сих пор мы раскладывали различные функции в степенные ряды, которые уже порядком поднадоели. И я чувствую, что настал момент, когда из стратегических запасов теории пора извлечь новые консервы. Нельзя ли разложить функцию в ряд как-нибудь по-другому? Например, выразить отрезок прямой линии через синусы и косинусы? Кажется невероятным, но такие, казалось бы, далекие друг от друга функции поддаются
«воссоединению». Помимо примелькавшихся степеней в теории и практике существуют и другие подходы к разложению функции в ряд.
На данном уроке мы познакомимся с тригонометрическим рядом Фурье, коснёмся вопроса его сходимости и суммы и, конечно же, разберём многочисленные примеры на разложение функций в ряд Фурье. Искренне хотелось назвать статью «Ряды Фурье для чайников», но это было бы лукавством, поскольку для решения задач потребуются знания других разделов математического анализа и некоторый практический опыт. Поэтому преамбула будет напоминать подготовку космонавтов =)
Во-первых, к изучению материалов страницы следует подойти в отличной форме. Выспавшимися, отдохнувшими и трезвыми. Без сильных эмоций по поводу сломанной лапы хомячка и навязчивых мыслей о тяготах жизни аквариумных рыбок. Ряд Фурье не сложен с точки зрения понимания, однако практические задания требуют просто повышенной концентрации внимания – в идеале следует полностью отрешиться от внешних раздражителей. Ситуация усугубляется тем, что не существует лёгкого способа проверки решения и ответа. Таким образом, если ваше самочувствие ниже среднего, то лучше заняться чем-нибудь попроще. Правда.
Во-вторых, перед полётом в космос необходимо изучить приборную панель космического корабля. Начнём со значений функций, которые должны щёлкаться на автомате:
![]()
При любом натуральном значении ![]() :
:
1) ![]() . И в самом деле, синусоида «прошивает» ось абсцисс через каждое «пи»:
. И в самом деле, синусоида «прошивает» ось абсцисс через каждое «пи»:
![]() . В случае отрицательных значений аргумента результат, само собой, будет таким же:
. В случае отрицательных значений аргумента результат, само собой, будет таким же: ![]() .
.
2) ![]() . А вот это знали не все. Косинус «пи эн» представляет собой эквивалент «мигалки»:
. А вот это знали не все. Косинус «пи эн» представляет собой эквивалент «мигалки»:
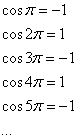
Отрицательный аргумент дела не меняет: ![]() .
.
Пожалуй, достаточно.
И, в-третьих, уважаемый отряд космонавтов, необходимо уметь… интегрировать.
В частности, уверенно подводить функцию под знак дифференциала, интегрировать по частям и быть в ладах с формулой Ньютона-Лейбница. Начнём важные предполётные упражнения. Категорически не рекомендую пропускать, чтобы потом не плющило в невесомости:
Пример 1
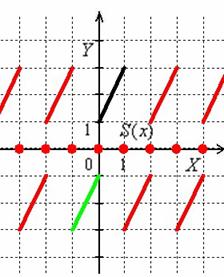
Вычислить определённые интегралы
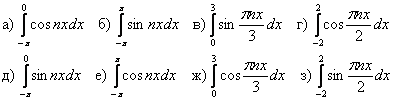
где ![]() принимает натуральные значения.
принимает натуральные значения.
Решение: интегрирование проводится по переменной «икс» и на данном этапе дискретная переменная «эн» считается константой. Во всех интегралах подводим функцию под знак дифференциала:
а) 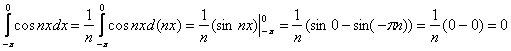
Перед применением формулы Ньютона-Лейбница полезно мысленно либо на черновике выполнить проверку. Используя правило дифференцирования сложной функции и не забывая, что ![]() – это константа, находим производную от первообразной:
– это константа, находим производную от первообразной:
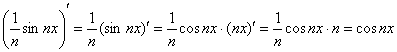 – получена исходная подынтегральная функция, как оно и должно быть.
– получена исходная подынтегральная функция, как оно и должно быть.
После интегрирования константа ![]() сразу выносится за скобки, и стандартная подстановка проходит без её участия: сначала в
сразу выносится за скобки, и стандартная подстановка проходит без её участия: сначала в ![]() вместо «икс» подставляем верхний предел (ноль), затем нижний предел («минус пи»). Синус нуля равен нулю, и как только что отмечалось,
вместо «икс» подставляем верхний предел (ноль), затем нижний предел («минус пи»). Синус нуля равен нулю, и как только что отмечалось, ![]() при любом натуральном «эн».
при любом натуральном «эн».
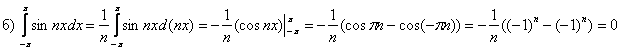
Кстати, результат тут виден сразу – интеграл от нечётной функции по симметричному относительно нуля отрезку равен нулю.
Не забываем о промежуточной проверке первообразной:
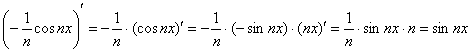
И на завершающем этапе даже лучше не проводить замены ![]() ,
,
а воспользоваться чётностью косинуса:
![]()
Крайне желательно научиться выполнять некоторые действия в уме и записывать решение сокращённо:
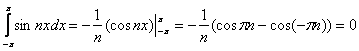
Желательно потому, что в рядах Фурье и без этого гелевый стержень опустеет.
Следующие два пункта отличаются усложнённой константой:
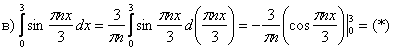
Проверка: 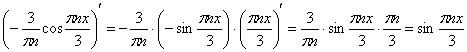
Подстановку распишу очень подробно:
![]()
Здесь на последнем этапе внесли «минус» в скобку и сделали ответ более компактным, возьмите на заметку этот приём. Также обратите внимание, что в результате применения формулы Ньютона-Лейбница, получено не число, а числовая последовательность.
Короткая версия решения, к которой хорошо бы пристреляться, выглядит так:
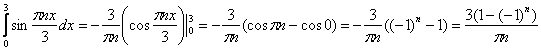
Привыкаем:
![]()
Четыре оставшихся пункта самостоятельно. Постарайтесь добросовестно отнестись к заданию и оформить интегралы коротким способом. Образцы решений в конце урока.
После КАЧЕСТВЕННОГО выполнения упражнений надеваем скафандры
и готовимся к старту!
Разложение функции в ряд Фурье на промежутке 
Рассмотрим некоторую функцию ![]() , которая определена по крайне мере на промежутке
, которая определена по крайне мере на промежутке ![]() (а, возможно, и на бОльшем промежутке). Если данная функция интегрируема на отрезке
(а, возможно, и на бОльшем промежутке). Если данная функция интегрируема на отрезке ![]() , то её можно разложить в тригонометрический ряд Фурье:
, то её можно разложить в тригонометрический ряд Фурье:
![]() , где
, где ![]() – так называемые коэффициенты Фурье.
– так называемые коэффициенты Фурье.
При этом число ![]() называют периодом разложения, а число
называют периодом разложения, а число ![]() – полупериодом разложения.
– полупериодом разложения.
Очевидно, что в общем случае ряд Фурье состоит из синусов и косинусов:
![]()
Действительно, распишем его подробно:
![]()
Нулевой член ряда принято записывать в виде ![]() .
.
Коэффициенты Фурье рассчитываются по следующим формулам:
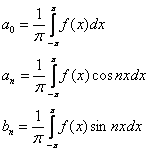
Прекрасно понимаю, что начинающим изучать тему пока малопонятны новые термины: период разложения, полупериод, коэффициенты Фурье и др. Без паники, это не сравнимо с волнением перед выходом в открытый космос. Во всём разберёмся в ближайшем примере, перед выполнением которого логично задаться насущными практическими вопросами:
Что нужно сделать в нижеследующих заданиях?
Разложить функцию ![]() в ряд Фурье. Дополнительно нередко требуется изобразить график функции
в ряд Фурье. Дополнительно нередко требуется изобразить график функции ![]() , график суммы ряда
, график суммы ряда ![]() , частичной суммы и в случае изощрённых профессорский фантазий – сделать что-нибудь ещё.
, частичной суммы и в случае изощрённых профессорский фантазий – сделать что-нибудь ещё.
Как разложить функцию в ряд Фурье?
По существу, нужно найти коэффициенты Фурье ![]() , то есть, составить и вычислить три определённых интеграла.
, то есть, составить и вычислить три определённых интеграла.
Пожалуйста, перепишите общий вид ряда Фурье и три рабочие формулы к себе в тетрадь. Я очень рад, что у некоторых посетителей сайта прямо на моих глазах осуществляется детская мечта стать космонавтом =)
Поехали:
Пример 2
Разложить функцию ![]() в ряд Фурье на промежутке
в ряд Фурье на промежутке ![]() . Построить график
. Построить график ![]() , график суммы ряда
, график суммы ряда ![]() и частичной суммы
и частичной суммы ![]() .
.
Решение: первая часть задания состоит в разложении функции в ряд Фурье.
Начало стандартное, обязательно записываем, что:
В данной задаче период разложения ![]() , полупериод
, полупериод ![]() .
.
Разложим функцию ![]() в ряд Фурье на промежутке
в ряд Фурье на промежутке ![]() :
:
![]()
Используя соответствующие формулы, найдём коэффициенты Фурье. Теперь нужно составить и вычислить три определённых интеграла. Для удобства я буду нумеровать пункты:
1) Первый интеграл самый простой, однако и он уже требует глаз да глаз:
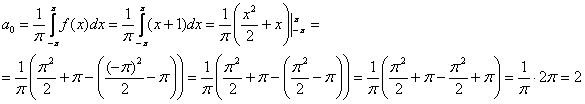
2) Используем вторую формулу:
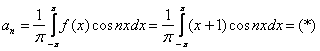
Данный интеграл хорошо знаком и берётся он по частям:
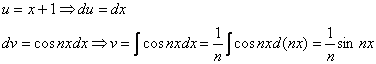
При нахождении ![]() использован метод подведения функции под знак дифференциала.
использован метод подведения функции под знак дифференциала.
В рассматриваемом задании сподручнее сразу использовать формулу интегрирования по частям в определённом интеграле 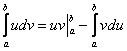 :
:
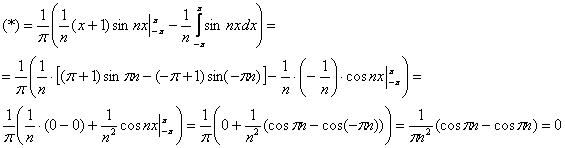
Пара технических замечаний. Во-первых, после применения формулы всё выражение нужно заключить в большие скобки, так как перед исходным интегралом находится константа ![]() . Не теряем её! Скобки можно раскрыть на любом дальнейшем шаге, я это сделал в самую последнюю очередь. В первом «куске»
. Не теряем её! Скобки можно раскрыть на любом дальнейшем шаге, я это сделал в самую последнюю очередь. В первом «куске» ![]() проявляем крайнюю аккуратность в подстановке, как видите, константа
проявляем крайнюю аккуратность в подстановке, как видите, константа ![]() не при делах, и пределы интегрирования подставляются в произведение
не при делах, и пределы интегрирования подставляются в произведение ![]() . Данное действие выделено квадратными скобками. Ну а интеграл
. Данное действие выделено квадратными скобками. Ну а интеграл  второго «куска» формулы вам хорошо знаком из тренировочного задания ;-)
второго «куска» формулы вам хорошо знаком из тренировочного задания ;-)
И самое главное – предельная концентрация внимания!
3) Ищем третий коэффициент Фурье:
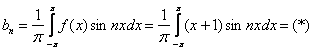
Получен родственник предыдущего интеграла, который тоже интегрируется по частям:
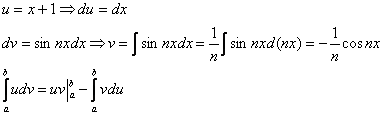
Этот экземпляр чуть сложнее, закомментирую дальнейшие действия пошагово:
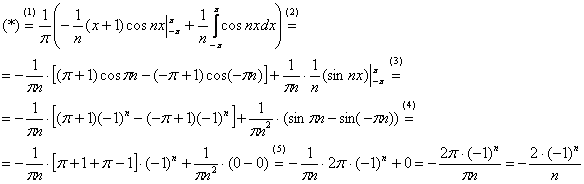
(1) Выражение 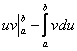 полностью заключаем в большие скобки. Не хотел показаться занудой, слишком уж часто теряют константу
полностью заключаем в большие скобки. Не хотел показаться занудой, слишком уж часто теряют константу ![]() .
.
(2) В данном случае я немедленно раскрыл эти большие скобки. Особое внимание уделяем первому «куску»: константа ![]() курит в сторонке и не участвует в подстановке пределов интегрирования (
курит в сторонке и не участвует в подстановке пределов интегрирования (![]() и
и ![]() ) в произведение
) в произведение ![]() . Ввиду загромождённости записи это действие снова целесообразно выделить квадратными скобками. Со вторым «куском»
. Ввиду загромождённости записи это действие снова целесообразно выделить квадратными скобками. Со вторым «куском» ![]() всё проще: здесь дробь
всё проще: здесь дробь ![]() появилась после раскрытия больших скобок, а константа
появилась после раскрытия больших скобок, а константа ![]() – в результате интегрирования знакомого интеграла ;-)
– в результате интегрирования знакомого интеграла ;-)
(3) В квадратных скобках проводим преобразования ![]() , а в правом интеграле – подстановку пределов интегрирования.
, а в правом интеграле – подстановку пределов интегрирования.
(4) Выносим «мигалку» из квадратных скобок: ![]() , после чего раскрываем внутренние скобки:
, после чего раскрываем внутренние скобки: ![]() .
.
(5) Взаимоуничтожаем 1 и –1 в скобках и проводим окончательные упрощения.
Наконец-то найдены все три коэффициента Фурье:
![]()
Подставим их в формулу ![]() :
:
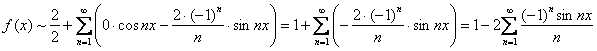
При этом не забываем разделить ![]() пополам. На последнем шаге константа («минус два»), не зависящая от «эн», вынесена за пределы суммы.
пополам. На последнем шаге константа («минус два»), не зависящая от «эн», вынесена за пределы суммы.
Таким образом, мы получили разложение функции ![]() в ряд Фурье на промежутке
в ряд Фурье на промежутке ![]() :
:
![]()
Изучим вопрос сходимости ряда Фурье. Я объясню теорию, в частности теорему Дирихле, буквально «на пальцах», поэтому если вам необходимы строгие формулировки, пожалуйста, обратитесь к учебнику по математическому анализу (например, 2-й том Бохана; или 3-й том Фихтенгольца, но в нём труднее).
Во второй части задачи требуется изобразить график ![]() , график суммы ряда
, график суммы ряда ![]() и график частичной суммы
и график частичной суммы ![]() .
.
График функции ![]() представляет собой обычную прямую на плоскости, которая проведена чёрным пунктиром:
представляет собой обычную прямую на плоскости, которая проведена чёрным пунктиром:
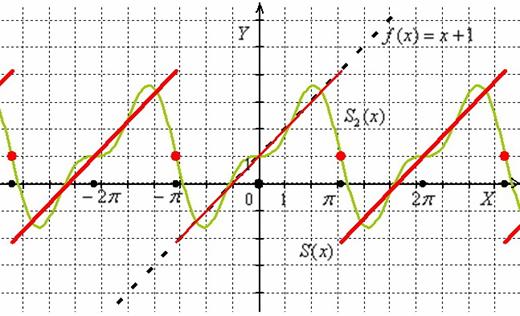
Разбираемся с суммой ряда ![]() . Как вы знаете, функциональные ряды сходятся к функциям. В нашем случае построенный ряд Фурье
. Как вы знаете, функциональные ряды сходятся к функциям. В нашем случае построенный ряд Фурье ![]() при любом значении «икс» сойдётся к функции
при любом значении «икс» сойдётся к функции ![]() , которая изображена красным цветом. Данная функция терпит разрывы 1-го рода в точках
, которая изображена красным цветом. Данная функция терпит разрывы 1-го рода в точках ![]() , но определена и в них (красные точки на чертеже)
, но определена и в них (красные точки на чертеже)
Таким образом: ![]() . Легко видеть, что
. Легко видеть, что ![]() заметно отличается от исходной функции
заметно отличается от исходной функции ![]() , именно поэтому в записи
, именно поэтому в записи ![]() ставится значок «тильда», а не знак равенства.
ставится значок «тильда», а не знак равенства.
Изучим алгоритм, по которому удобно строить сумму ряда.
На центральном интервале ![]() ряд Фурье сходится к самой функции
ряд Фурье сходится к самой функции ![]() (центральный красный отрезок совпадает с чёрным пунктиром линейной функции).
(центральный красный отрезок совпадает с чёрным пунктиром линейной функции).
Теперь немного порассуждаем о природе рассматриваемого тригонометрического разложения. В ряд Фурье ![]() входят только периодические функции (константа, синусы и косинусы), поэтому сумма ряда
входят только периодические функции (константа, синусы и косинусы), поэтому сумма ряда ![]() тоже представляет собой периодическую функцию.
тоже представляет собой периодическую функцию.
Что это значит в нашем конкретном примере? А это обозначает то, что сумма ряда ![]() – непременно периодична и красный отрезок интервала
– непременно периодична и красный отрезок интервала ![]() обязан бесконечно повторяться слева и справа.
обязан бесконечно повторяться слева и справа.
Думаю, сейчас окончательно прояснился смысл фразы «период разложения ![]() ». Упрощённо говоря, через каждые
». Упрощённо говоря, через каждые ![]() ситуация вновь и вновь повторяется.
ситуация вновь и вновь повторяется.
На практике обычно достаточно изобразить три периода разложения, как это сделано на чертеже. Ну и ещё «обрубки» соседних периодов – чтобы было понятно, что график продолжается.
Особый интерес представляют точки разрыва 1-го рода. В таких точках ряд Фурье сходится к изолированным значениям, которые расположены ровнёхонько посередине «скачка» разрыва (красные точки на чертеже). Как узнать ординату этих точек? Сначала найдём ординату «верхнего этажа»: для этого вычислим значение функции в крайней правой точке центрального периода разложения: ![]() . Чтобы вычислить ординату «нижнего этажа» проще всего взять крайнее левое значение этого же периода:
. Чтобы вычислить ординату «нижнего этажа» проще всего взять крайнее левое значение этого же периода: ![]() . Ордината среднего значения – это среднее арифметическое суммы «верха и низа»:
. Ордината среднего значения – это среднее арифметическое суммы «верха и низа»: ![]() . Приятным является тот факт, что при построении чертежа вы сразу увидите, правильно или неправильно вычислена середина.
. Приятным является тот факт, что при построении чертежа вы сразу увидите, правильно или неправильно вычислена середина.
Построим частичную сумму ряда ![]() и заодно повторим смысл термина «сходимость». Мотив известен ещё из урока о сумме числового ряда. Распишем наше богатство подробно:
и заодно повторим смысл термина «сходимость». Мотив известен ещё из урока о сумме числового ряда. Распишем наше богатство подробно:
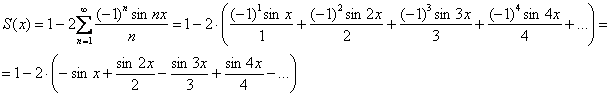
Чтобы составить частичную сумму ![]() необходимо записать нулевой + ещё два члена ряда. То есть,
необходимо записать нулевой + ещё два члена ряда. То есть, ![]()
На чертеже график функции ![]() изображен зелёным цветом, и, как видите, он достаточно плотно «обвивает» полную сумму
изображен зелёным цветом, и, как видите, он достаточно плотно «обвивает» полную сумму ![]() . Если рассмотреть частичную сумму из пяти членов ряда
. Если рассмотреть частичную сумму из пяти членов ряда ![]() , то график этой функции будет ещё точнее приближать красные линии, если сто членов
, то график этой функции будет ещё точнее приближать красные линии, если сто членов ![]() – то «зелёный змий» фактически полностью сольётся с красными отрезками и т.д. Таким образом, ряд Фурье сходится к своей сумме
– то «зелёный змий» фактически полностью сольётся с красными отрезками и т.д. Таким образом, ряд Фурье сходится к своей сумме ![]() .
.
Интересно отметить, что любая частичная сумма ![]() – это непрерывная функция, однако полная сумма ряда
– это непрерывная функция, однако полная сумма ряда ![]() всё же разрывна.
всё же разрывна.
На практике не так уж редко требуется построить и график частичной суммы. Как это сделать? В нашем случае необходимо рассмотреть функцию ![]() на отрезке
на отрезке ![]() , вычислить её значения на концах отрезка и в промежуточных точках (чем больше точек рассмотрите – тем точнее будет график). Затем следует отметить данные точки на чертеже и аккуратно изобразить график
, вычислить её значения на концах отрезка и в промежуточных точках (чем больше точек рассмотрите – тем точнее будет график). Затем следует отметить данные точки на чертеже и аккуратно изобразить график ![]() на периоде
на периоде ![]() , после чего «растиражировать» его на соседние промежутки. А как иначе? Ведь приближение
, после чего «растиражировать» его на соседние промежутки. А как иначе? Ведь приближение ![]() – это тоже периодическая функция… …чем-то мне её график напоминает ровный ритм сердца на дисплее медицинского прибора.
– это тоже периодическая функция… …чем-то мне её график напоминает ровный ритм сердца на дисплее медицинского прибора.
Выполнять построение, конечно, не сильно удобно, так как ![]() и приходится проявлять сверхаккуратность, выдерживая точность не меньше, чем до половины миллиметра. Впрочем, читателей, которые не в ладах с черчением, обрадую – в «реальной» задаче выполнять чертёж нужно далеко не всегда, где-то в 50% случаев требуется разложить функцию в ряд Фурье и всё.
и приходится проявлять сверхаккуратность, выдерживая точность не меньше, чем до половины миллиметра. Впрочем, читателей, которые не в ладах с черчением, обрадую – в «реальной» задаче выполнять чертёж нужно далеко не всегда, где-то в 50% случаев требуется разложить функцию в ряд Фурье и всё.
После выполнения чертежа завершаем задание:
Ответ: ![]()
Во многих задачах функция терпит разрыв 1-го рода прямо на периоде разложения:
Пример 3
Разложить в ряд Фурье функцию ![]() , заданную на отрезке
, заданную на отрезке ![]() . Начертить график функции и полной суммы ряда.
. Начертить график функции и полной суммы ряда.
![]()
Предложенная функция задана кусочным образом (причём, заметьте, только на отрезке ![]() ) и терпит разрыв 1-го рода в точке
) и терпит разрыв 1-го рода в точке ![]() . Можно ли вычислить коэффициенты Фурье? Без проблем. И левая
. Можно ли вычислить коэффициенты Фурье? Без проблем. И левая ![]() и правая
и правая ![]() части функции интегрируемы на своих промежутках, поэтому интегралы в каждой из трёх формул следует представить в виде суммы двух интегралов. Посмотрим, например, как это делается у нулевого коэффициента:
части функции интегрируемы на своих промежутках, поэтому интегралы в каждой из трёх формул следует представить в виде суммы двух интегралов. Посмотрим, например, как это делается у нулевого коэффициента:
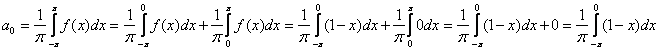
Второй интеграл оказался равным нулю, что убавило работы, но так бывает далеко не всегда.
Аналогично расписываются два других коэффициента Фурье.
Как изобразить сумму ряда? На левом интервале ![]() чертим отрезок прямой
чертим отрезок прямой ![]() , а на интервале
, а на интервале ![]() – отрезок прямой
– отрезок прямой ![]() (жирно-жирно выделяем участок оси
(жирно-жирно выделяем участок оси ![]() ). То есть, на промежутке разложения
). То есть, на промежутке разложения ![]() сумма ряда
сумма ряда ![]() совпадает с функцией
совпадает с функцией ![]() везде, кроме трёх «нехороших» точек. В точке разрыва функции
везде, кроме трёх «нехороших» точек. В точке разрыва функции ![]() ряд Фурье сойдётся к изолированному значению, которое располагается ровно посередине «скачка» разрыва. Его нетрудно увидеть и устно: левосторонний предел:
ряд Фурье сойдётся к изолированному значению, которое располагается ровно посередине «скачка» разрыва. Его нетрудно увидеть и устно: левосторонний предел: ![]() , правосторонний предел:
, правосторонний предел: ![]() и, очевидно, что ордината средней точки равна 0,5.
и, очевидно, что ордината средней точки равна 0,5.
В силу периодичности суммы ![]() , картинку необходимо «размножить» на соседние периоды, в частности изобразить то же самое на интервалах
, картинку необходимо «размножить» на соседние периоды, в частности изобразить то же самое на интервалах ![]() и
и ![]() . При этом, в точках
. При этом, в точках ![]() ряд Фурье сойдётся к срединным значениям.
ряд Фурье сойдётся к срединным значениям.
По сути-то ничего нового здесь нет.
Постарайтесь самостоятельно справиться с данной задачей. Примерный образец чистового оформления и чертёж в конце урока.
Далее возникает закономерный вопрос: если схема работает на отрезке ![]() , то почему бы её не применить к разложению функций в ряд Фурье на промежутках
, то почему бы её не применить к разложению функций в ряд Фурье на промежутках ![]() или на каком-нибудь другом периоде?
или на каком-нибудь другом периоде?
Разложение функции в ряд Фурье на произвольном периоде
Для произвольного периода разложения ![]() , где «эль» – любое положительное число, формулы ряда Фурье и коэффициентов Фурье отличаются немного усложнённым аргументом синуса и косинуса:
, где «эль» – любое положительное число, формулы ряда Фурье и коэффициентов Фурье отличаются немного усложнённым аргументом синуса и косинуса:

Если ![]() , то получаются формулы промежутка
, то получаются формулы промежутка ![]() , с которых мы начинали.
, с которых мы начинали.
Алгоритм и принципы решения задачи полностью сохраняются, но возрастает техническая сложность вычислений:
Пример 4
Разложить функцию ![]() в ряд Фурье и построить график суммы.
в ряд Фурье и построить график суммы.
![]()
Решение: фактически аналог Примера № 3 с разрывом 1-го рода в точке ![]() . В данной задаче период разложения
. В данной задаче период разложения ![]() , полупериод
, полупериод ![]() . Функция определена только на полуинтервале
. Функция определена только на полуинтервале ![]() , но это не меняет дела – важно, что оба куска функции интегрируемы.
, но это не меняет дела – важно, что оба куска функции интегрируемы.
Разложим функцию в ряд Фурье:
![]()
Поскольку функция разрывна в начале координат, то каждый коэффициент Фурье очевидным образом следует записать в виде суммы двух интегралов:
1) Первый интеграл распишу максимально подробно:
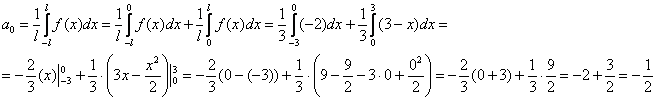
2) Тщательным образом вглядываемся в поверхность Луны:
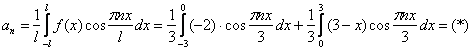
Второй интеграл берём по частям:
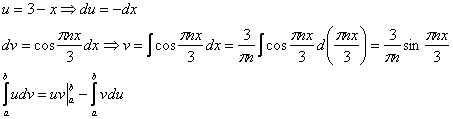
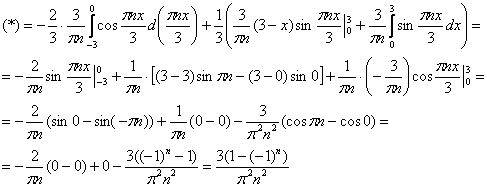
На что следует обратить пристальное внимание, после того, как мы звёздочкой ![]() открываем продолжение решения?
открываем продолжение решения?
Во-первых, не теряем первый интеграл 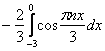 , где сразу же выполняем подведение под знак дифференциала. Во-вторых, не забываем злополучную константу
, где сразу же выполняем подведение под знак дифференциала. Во-вторых, не забываем злополучную константу ![]() перед большими скобками и не путаемся в знаках при использовании формулы
перед большими скобками и не путаемся в знаках при использовании формулы 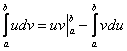 . Большие скобки, всё-таки удобнее раскрывать сразу же на следующем шаге.
. Большие скобки, всё-таки удобнее раскрывать сразу же на следующем шаге.
Остальное дело техники, затруднения может вызвать только недостаточный опыт решения интегралов.
Да, не зря именитые коллеги французского математика Фурье возмущались – как это тот посмел раскладывать функции в тригонометрические ряды?! =) К слову, наверное, всем интересен практический смысл рассматриваемого задания. Сам Фурье работал над математической моделью теплопроводности, а впоследствии ряд, названный его именем стал применяться для исследования многих периодических процессов, коих в окружающем мире видимо-невидимо. Сейчас, кстати, поймал себя на мысли, что не случайно сравнил график второго примера с периодическим ритмом сердца. Желающие могут ознакомиться с практическим применением преобразования Фурье в сторонних источниках. …Хотя лучше не надо – будет вспоминаться, как Первая Любовь =)
3) Учитывая неоднократно упоминавшиеся слабые звенья, разбираемся с третьим коэффициентом:
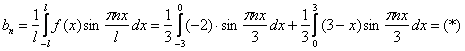
Интегрируем по частям:
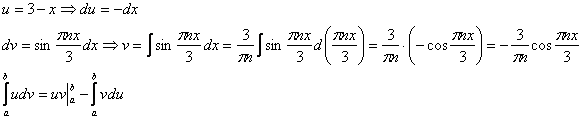
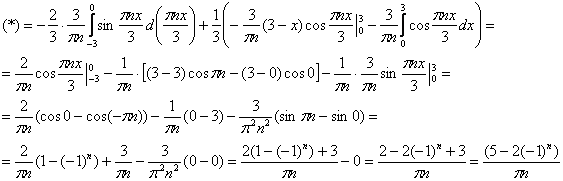
Подставим найдённые коэффициенты Фурье ![]() в формулу
в формулу ![]() , не забывая поделить нулевой коэффициент пополам:
, не забывая поделить нулевой коэффициент пополам:
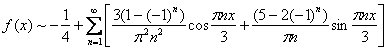
Построим график суммы ряда. Кратко повторим порядок действий: на интервале ![]() строим прямую
строим прямую ![]() , а на интервале
, а на интервале ![]() – прямую
– прямую ![]() . При нулевом значении «икс» ставим точку посередине «скачка» разрыва
. При нулевом значении «икс» ставим точку посередине «скачка» разрыва ![]() и «тиражируем» график на соседние периоды:
и «тиражируем» график на соседние периоды:
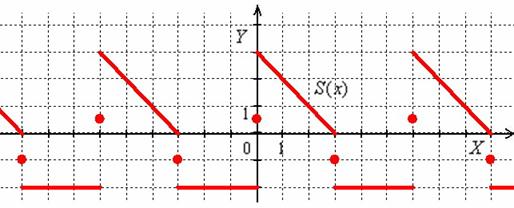
На «стыках» периодов ![]() сумма также будет равна серединам «скачка» разрыва
сумма также будет равна серединам «скачка» разрыва ![]() .
.
Готово. Напоминаю, что сама функция по условию определена только на полуинтервале ![]() и, очевидно, совпадает с суммой ряда на интервалах
и, очевидно, совпадает с суммой ряда на интервалах ![]()
Ответ: 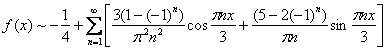
Иногда кусочно-заданная функция бывает и непрерывна на периоде разложения. Простейший образец: ![]() . Решение (см. 2-й том Бохана) такое же, как и двух предыдущих примерах: несмотря на непрерывность функции в точке
. Решение (см. 2-й том Бохана) такое же, как и двух предыдущих примерах: несмотря на непрерывность функции в точке ![]() , каждый коэффициент Фурье выражается суммой двух интегралов.
, каждый коэффициент Фурье выражается суммой двух интегралов.
На промежутке разложения точек разрыва 1-го рода и/или точек «стыка» графика может быть и больше (две, три и вообще любое конечное количество). Если функция интегрируема на каждой части, то она также разложима в ряд Фурье. Но из практического опыта такую жесть что-то не припоминаю. Тем не менее, встречаются более трудные задания, чем только что рассмотренное, и в конце статьи для всех желающих есть ссылки на ряды Фурье повышенной сложности.
А пока расслабимся, откинувшись в креслах и созерцая бескрайние звёздные просторы:
Пример 5
Разложить функцию ![]() в ряд Фурье на промежутке
в ряд Фурье на промежутке ![]() и построить график суммы ряда.
и построить график суммы ряда.
В данной задаче функция непрерывна на полуинтервале разложения, что упрощает решение. Всё очень похоже на Пример № 2. С космического корабля никуда не деться – придётся решать =) Примерный образец оформления в конце урока, график прилагается.
Разложение в ряд Фурье чётных и нечётных функций
С чётными и нечётными функциями процесс решения задачи заметно упрощается. И вот почему. Вернёмся к разложению функции в ряд Фурье на периоде «два пи» ![]() и произвольном периоде «два эль»
и произвольном периоде «два эль» ![]() .
.
Предположим, что наша функция ![]() чётна. Общий же член ряда, как вы видите, содержит чётные косинусы и нечётные синусы. А если мы раскладываем ЧЁТНУЮ функцию, то зачем нам нечётные синусы?! Давайте обнулим ненужный коэффициент:
чётна. Общий же член ряда, как вы видите, содержит чётные косинусы и нечётные синусы. А если мы раскладываем ЧЁТНУЮ функцию, то зачем нам нечётные синусы?! Давайте обнулим ненужный коэффициент: ![]() .
.
Таким образом, чётная функция раскладывается в ряд Фурье только по косинусам:

Поскольку интегралы от чётных функций по симметричному относительно нуля отрезку интегрирования можно удваивать, то упрощаются и остальные коэффициенты Фурье.
Для промежутка ![]() :
:
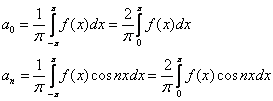
Для произвольного промежутка:

К хрестоматийным примерам, которые есть практически в любом учебнике по матанализу, относятся разложения чётных функций ![]() . Кроме того, они неоднократно встречались и в моей личной практике:
. Кроме того, они неоднократно встречались и в моей личной практике:
Пример 6
Дана функция ![]() . Требуется:
. Требуется:
1) разложить функцию в ряд Фурье с периодом ![]() , где
, где ![]() – произвольное положительное число;
– произвольное положительное число;
2) записать разложение на промежутке ![]() , построить функцию
, построить функцию ![]() и график полной суммы ряда
и график полной суммы ряда ![]() .
.
Решение: в первом пункте предлагается решить задачу в общем виде, и это очень удобно! Появится надобность – просто подставьте своё значение.
1) В данной задаче период разложения ![]() , полупериод
, полупериод ![]() . В ходе дальнейших действий, в частности при интегрировании, «эль» считается константой
. В ходе дальнейших действий, в частности при интегрировании, «эль» считается константой
Функция ![]() является чётной, а значит, раскладывается в ряд Фурье только по косинусам:
является чётной, а значит, раскладывается в ряд Фурье только по косинусам: ![]() .
.
Коэффициенты Фурье ищем по формулам 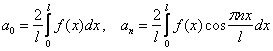 . Обратите внимание на их безусловные преимущества. Во-первых, интегрирование проводится по положительному отрезку разложения, а значит, мы благополучно избавляемся от модуля
. Обратите внимание на их безусловные преимущества. Во-первых, интегрирование проводится по положительному отрезку разложения, а значит, мы благополучно избавляемся от модуля ![]() , рассматривая из двух кусков только «икс». И, во-вторых, заметно упрощается интегрирование.
, рассматривая из двух кусков только «икс». И, во-вторых, заметно упрощается интегрирование.
Раз:
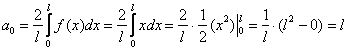
Два:
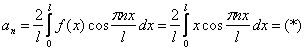
Интегрируем по частям:
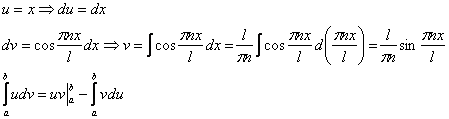
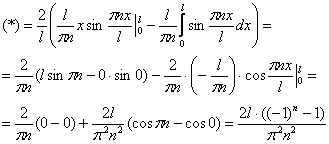
Таким образом:
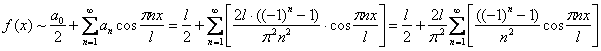 , при этом константу
, при этом константу ![]() , которая не зависит от «эн», выносим за пределы суммы.
, которая не зависит от «эн», выносим за пределы суммы.
Ответ: 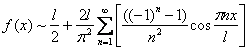
2) Запишем разложение ![]() на промежутке
на промежутке ![]() , для этого в общую формулу подставляем нужное значение полупериода
, для этого в общую формулу подставляем нужное значение полупериода ![]() :
:
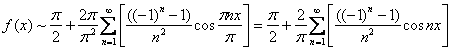
В данном случае сумма ряда непрерывна, и, разумеется, чётна. Построение графика ![]() вряд ли нуждается в комментариях:
вряд ли нуждается в комментариях:
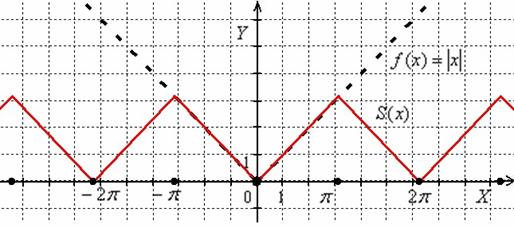
Хотел ещё построить частичную сумму ![]() , но её график практически совпал с «красной пилой» – настолько хорошо уже такое малое количество слагаемых приближает полную сумму.
, но её график практически совпал с «красной пилой» – настолько хорошо уже такое малое количество слагаемых приближает полную сумму.
Ответ: 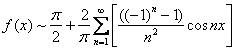
Думаю, все представили, как «водят хороводы» параболы при разложении функции ![]() . И, чтобы никому не было обидно, я прикреплю этот пример к дополнительным материалам.
. И, чтобы никому не было обидно, я прикреплю этот пример к дополнительным материалам.
Если ![]() – нечётная функция, то в разложениях Фурье
– нечётная функция, то в разложениях Фурье ![]() ,
, ![]() оказываются лишними чётные косинусы, из чего следует равенство
оказываются лишними чётные косинусы, из чего следует равенство ![]() . Более того, коэффициент
. Более того, коэффициент ![]() тоже равен нулю, в чём легко убедиться аналитически: интеграл от нечётной функции по симметричному относительно нуля отрезку равен нулю:
тоже равен нулю, в чём легко убедиться аналитически: интеграл от нечётной функции по симметричному относительно нуля отрезку равен нулю: 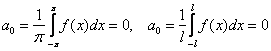 .
.
Таким образом, нечётная функция раскладывается в ряд Фурье только по синусам:
![]() на промежутке
на промежутке ![]() или
или ![]() на произвольном периоде.
на произвольном периоде.
При этом необходимо вычислить единственный коэффициент Фурье:
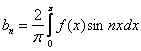 или
или 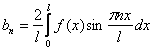 соответственно.
соответственно.
Небольшая миниатюра для самостоятельного решения:
Пример 7
Разложить функцию в ряд Фурье и построить график суммы ряда не менее чем на трёх периодах
![]()
Решение и ответ в конце урока.
Разложение чётной функции часто маскируют типовой формулировкой, пример:
Разложить функцию ![]() в ряд Фурье по косинусам на промежутке
в ряд Фурье по косинусам на промежутке ![]() .
.
Если по условию не нужно чертежа, тихой сапой применяем формулы 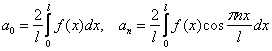 и даём ответ в виде
и даём ответ в виде ![]() . Про чётность можно скромно умолчать ;-)
. Про чётность можно скромно умолчать ;-)
Но если дополнительно требуется построить график суммы, то необходимо понимать следующее: разложение по косинусам отобразит отрезок прямой ![]() (чёрная линия) чётным образом (симметрично относительно оси
(чёрная линия) чётным образом (симметрично относительно оси ![]() ) на интервал
) на интервал ![]() (зелёная линия), и, очевидно, функция
(зелёная линия), и, очевидно, функция ![]() будет иметь непрерывный пилообразный график:
будет иметь непрерывный пилообразный график:
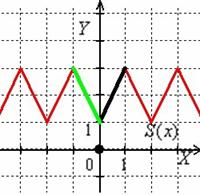
В ряде случаев симметричное продолжение функции надо записать аналитически. Начинающим рекомендую графический метод: сначала на промежутке ![]() чертим отрезок прямой
чертим отрезок прямой ![]() , затем, симметрично относительно оси ординат – его «зелёного» коллегу. Находим уравнение прямой
, затем, симметрично относительно оси ординат – его «зелёного» коллегу. Находим уравнение прямой ![]() , которая содержит зелёный отрезок (устно, или, например, по двум точкам).
, которая содержит зелёный отрезок (устно, или, например, по двум точкам).
Таким образом, эта же задача может быть сформулирована по-другому:
Разложить функцию ![]() в ряд Фурье.
в ряд Фурье.
Кстати, эта интерпретация вообще коварно умалчивает о чётности функции и может наказать двойным объёмом работы по общим формулам ;-) Поэтому в случае подозрительной похожести кусков функции (а чайникам – в любом случае!) имеет смысл сразу же изобразить её на чертеже.
Условие чётности ![]() нетрудно проверить и аналитически. В левую часть функции подставляем «минус икс»:
нетрудно проверить и аналитически. В левую часть функции подставляем «минус икс»: ![]() – в результате чего «на выходе» получаем правую часть.
– в результате чего «на выходе» получаем правую часть.
Решение данного примера есть в соответствующем архиве (Папка Ряды_7), который можно бесплатно закачать на странице Готовые задачи по высшей математике.
Аналогично вуалируется нечётность:
Разложить функцию ![]() в ряд Фурье по синусам на промежутке
в ряд Фурье по синусам на промежутке ![]() .
.
Если чертёж не нужен, ищем коэффициент 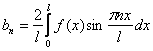 и записываем ответ в виде
и записываем ответ в виде ![]() . О нечётности снова молчок ;-) Однако в любом случае полезно знать следующее: разложение по синусам отобразит отрезок прямой
. О нечётности снова молчок ;-) Однако в любом случае полезно знать следующее: разложение по синусам отобразит отрезок прямой ![]() (чёрная линия) нечётным образом (симметрично относительно начала координат) на интервал
(чёрная линия) нечётным образом (симметрично относительно начала координат) на интервал ![]() (зелёная линия). И внимательный читатель статьи без труда изобразит график суммы ряда:
(зелёная линия). И внимательный читатель статьи без труда изобразит график суммы ряда:
Составим уравнение «зелёного» продолжения (например, по предложенному в предыдущем пункте алгоритму) и перепишем задачу в эквивалентной формулировке:
Разложить функцию ![]() в ряд Фурье.
в ряд Фурье.
Выглядит опять провокационно, и если вам встретилось похожее условие, то сначала постройте график функции и изучите его на предмет симметрии – чтобы не пришлось использовать общие формулы разложения.
Проверим условие нечётности ![]() аналитически, для этого в левый кусок функции подставляем «минус икс»:
аналитически, для этого в левый кусок функции подставляем «минус икс»: ![]() – в результате чего «на выходе» получается правый кусок с противоположным знаком.
– в результате чего «на выходе» получается правый кусок с противоположным знаком.
Вот, пожалуй, и все основные сведения о рядах Фурье, которых должно хватить для решения многих практических примеров. Надо сказать, что материал был непростой, причём изложить его доступно тоже было далеко не просто. Но вроде получилось неплохо.
Наш полёт подошёл к концу, и есть такое подозрение, что немалая часть экипажа хочет отправиться в экспедицию на Марс =) Дополнительные задачи с решениями можно закачать в Банке готовых работ, причём среди них есть и более редкие задания по теме – нахождение спектра амплитуд, суммы ряда в различных точках и т.д. Кроме того, я создал дополнительную pdf-ку, в которую включил примеры, не вошедшие в статью (всё-таки нужно соблюдать разумные рамки), а также ряды Фурье повышенной сложности, в своё время решённые на заказ студентам солидного технического ВУЗа.
Удачного путешествия – и обязательно возвращайтесь!
Решения и ответы:
Пример 1: Решение:
Пример 3: Решение: В данной задаче период разложения ![]() , полупериод
, полупериод ![]() . Разложим функцию в ряд Фурье:
. Разложим функцию в ряд Фурье: ![]() .
.
Используя соответствующие формулы, вычислим коэффициенты Фурье:
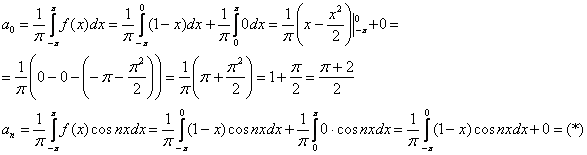
Интегрируем по частям:
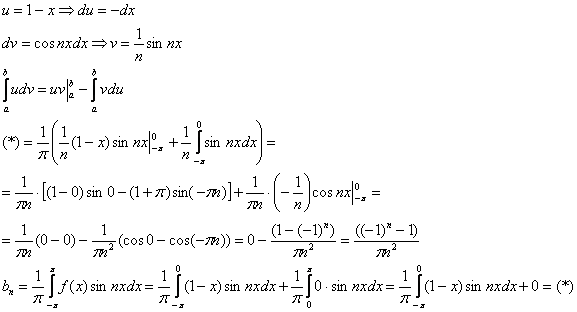
Интегрируем по частям:
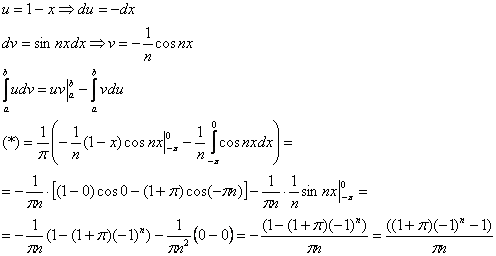
Искомое разложение имеет вид:
![]()
В данном случае:
![]()
Изобразим на чертеже исходную функцию (чёрный пунктир/точки) и график суммы ряда:
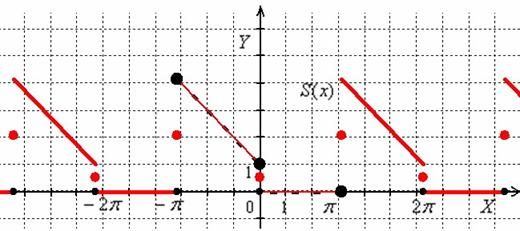
Ответ: ![]()
Пример 5: Решение: в данной задаче период разложения ![]() , полупериод
, полупериод ![]() .
.
Разложим функцию в ряд Фурье:
![]()
Используя соответствующие формулы, вычислим коэффициенты Фурье:
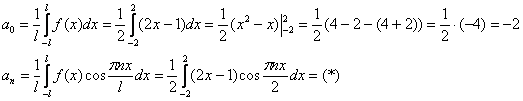
Интегрируем по частям:
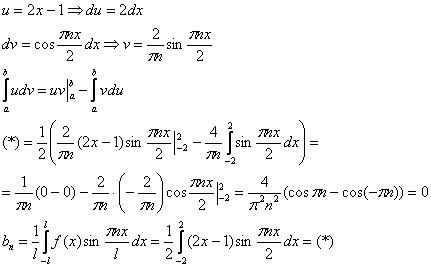
Интегрируем по частям:
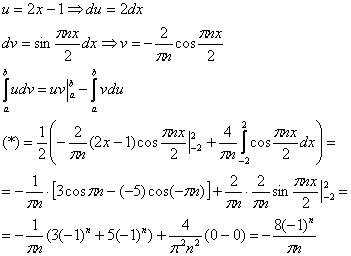
Таким образом:
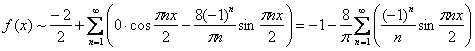
Изобразим на чертеже сумму ряда:
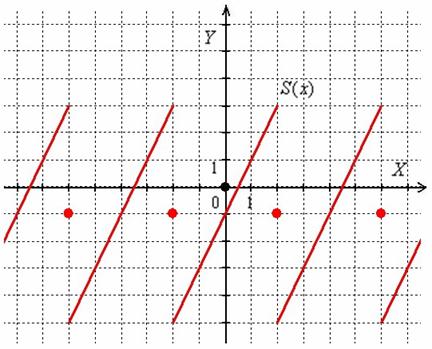
Ответ: 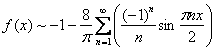
Пример 7: Решение: в данной задаче период разложения ![]() , полупериод
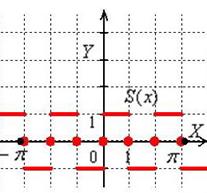
, полупериод ![]() . Функция является нечётной, а значит, раскладывается в ряд Фурье только по синусам:
. Функция является нечётной, а значит, раскладывается в ряд Фурье только по синусам: ![]() .
.
Вычислим коэффициент Фурье:
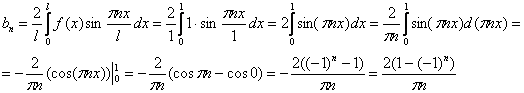
Таким образом: 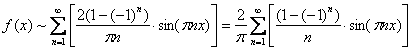
Построим график суммы ряда:
Ответ: 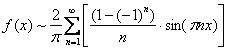
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
