
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как отобразить линию и область с помощью комплексной функции?
Минуту ещё, мой ветер не стих,
Мне нравится здесь, в королевстве кривых (с)
Для начала расшифруем заголовок :) Вспоминаем определение с первого урока:
функцией комплексной переменной называют правило (закон) ![]() , по которому каждому допустимому комплексному значению
, по которому каждому допустимому комплексному значению ![]() ставится в соответствие одно или бОльшее количество значений
ставится в соответствие одно или бОльшее количество значений ![]() .
.
Так, функция ![]() каждому комплексному «зет» ставит в соответствие одно значение «дубльвэ». К примеру, число
каждому комплексному «зет» ставит в соответствие одно значение «дубльвэ». К примеру, число ![]() по правилу
по правилу ![]() превращается в число
превращается в число ![]() . Геометрически это выглядит так:
. Геометрически это выглядит так:
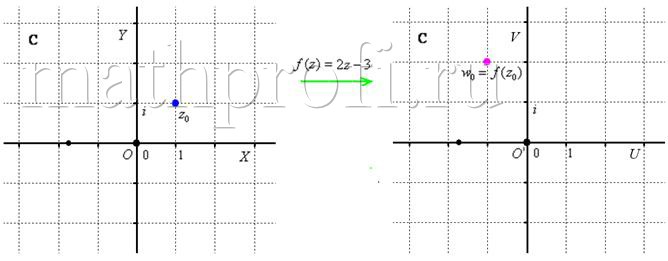
И наша сегодняшняя задача состоит в том, чтобы научиться отображать с помощью функций не отдельно взятые точки, а целые линии и более того – области. Напоминаю, что линию можно задать уравнением ![]() (как вариант, функцией
(как вариант, функцией ![]() ), присоединив к исходной комплексной плоскости (слева) декартову систему координат
), присоединив к исходной комплексной плоскости (слева) декартову систему координат ![]() . Также в ходу параметрическое задание линии:
. Также в ходу параметрическое задание линии: ![]() , а-ка
, а-ка ![]() .
.
Пример 1
С помощью функции ![]() отобразить линии:
отобразить линии:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() , …пожалуй, достаточно.
, …пожалуй, достаточно.
Решение: а) Отобразим прямую ![]() , то бишь ось
, то бишь ось ![]() с декартовым уравнением
с декартовым уравнением ![]() . Когда прямая параллельна координатным осям либо задаёт саму ось, удобно использовать прямое рассуждение. Так как
. Когда прямая параллельна координатным осям либо задаёт саму ось, удобно использовать прямое рассуждение. Так как ![]() , то
, то ![]() , и коль скоро
, и коль скоро ![]() , то имеем функцию
, то имеем функцию ![]() .
.
Таким образом, действительные значения «икс» (точки оси ![]() ) переходят в действительные значения
) переходят в действительные значения ![]() – точки действительной оси
– точки действительной оси ![]() . При этом имеет место несоответствие значений, так, если
. При этом имеет место несоответствие значений, так, если ![]() , то
, то ![]() . Но, так или иначе, функция
. Но, так или иначе, функция ![]() отображает ось
отображает ось ![]() в ось
в ось ![]() .
.
Как вариант (может даже лучший), ось ![]() можно записать в параметрической форме:
можно записать в параметрической форме: ![]() и подставив эти уравнения в
и подставив эти уравнения в ![]() :
:
![]() – получаем функцию в параметрическом виде.
– получаем функцию в параметрическом виде.
При изменении параметра «тэ» от «минус» до «плюс» бесконечности точки оси ![]() непрерывно отображаются в точки
непрерывно отображаются в точки ![]() оси
оси ![]() .
.
б) При отображении прямой ![]() (оси
(оси ![]() ) рассуждения «зеркальны»: поскольку
) рассуждения «зеркальны»: поскольку ![]() , то:
, то:
![]() – в результате значения «игрек» (точки оси
– в результате значения «игрек» (точки оси ![]() ) переходят во множество комплексных чисел с одинаковой действительной частью. А именно, это числа, лежащие на прямой
) переходят во множество комплексных чисел с одинаковой действительной частью. А именно, это числа, лежащие на прямой ![]() , параллельной оси
, параллельной оси ![]() (синяя линия на чертеже ниже).
(синяя линия на чертеже ниже).
Таким образом, ось ![]() отображается в прямую
отображается в прямую ![]() плоскости
плоскости ![]() .
.
Как вариант, можно использовать параметрическое уравнение оси ![]() , получив функцию в виде
, получив функцию в виде ![]() с тем же самым выводом.
с тем же самым выводом.
То были простые случаи, теперь общее правило. Чтобы отобразить линию ![]() плоскости
плоскости ![]() на плоскость
на плоскость ![]() с помощью функции
с помощью функции ![]() , нужно составить и решить следующую систему:
, нужно составить и решить следующую систему:
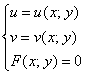 , где
, где ![]() – действительная часть функции
– действительная часть функции ![]() , а
, а ![]() – её мнимая часть. Это рабочие формулы (1), пожалуйста, перепишите их к себе на листок.
– её мнимая часть. Это рабочие формулы (1), пожалуйста, перепишите их к себе на листок.
Алгоритм решения состоит в том, чтобы исключить из этих уравнений «икс» и «игрек» и связать между собой переменные «у» и «вэ», получив линию ![]() на плоскости
на плоскости ![]() .
.
Действительная и мнимая часть функции ![]() уже найдены:
уже найдены:
![]()
![]()
и осталось перекоцать линии, предложенные в условии:
в) Отобразим с помощью функции ![]() прямую
прямую ![]() . Составим соответствующую систему:
. Составим соответствующую систему:
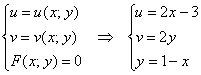
Решение начинают с последнего уравнения – тут у нас готовенький «игрек» ![]() , который мы подставляем во 2-е уравнение:
, который мы подставляем во 2-е уравнение:
![]() – теперь из 1-го уравнения выражаем «икс»:
– теперь из 1-го уравнения выражаем «икс»: ![]() – и подставляем его в то же 2-е уравнение:
– и подставляем его в то же 2-е уравнение:
![]()
Таким образом, прямая ![]() отобразилась в прямую
отобразилась в прямую ![]() (зелёный цвет на чертеже ниже). Прямую
(зелёный цвет на чертеже ниже). Прямую ![]() строим привычным образом в декартовой системе координат
строим привычным образом в декартовой системе координат ![]() , где роль независимой переменной играет
, где роль независимой переменной играет ![]() , а роль зависимой –
, а роль зависимой – ![]() .
.
г) Отобразим каноническую параболу ![]() :
:
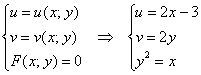
«Разворачиваем» последнее уравнение: ![]() и подставляем в 1-е:
и подставляем в 1-е:
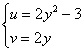
Из 2-го уравнения выражаем ![]() – подставляем в 1-е:
– подставляем в 1-е:
![]()
Таким образом, парабола ![]() отобразилась в параболу
отобразилась в параболу ![]() (оранжевый цвет на чертеже ниже).
(оранжевый цвет на чертеже ниже).
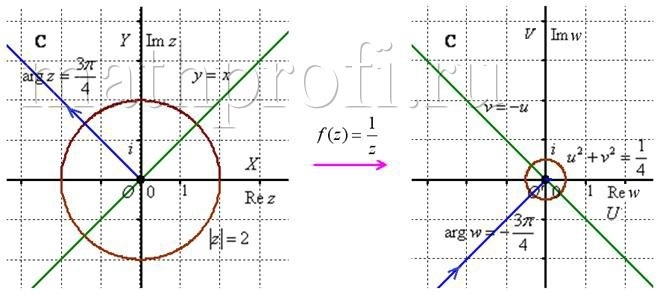
д) И, наконец, отобразим единичную окружность ![]() с известным декартовым уравнением:
с известным декартовым уравнением:
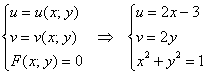
Плясать начинаем от третьего уравнения, и тут есть выбор: выразить «икс» через «игрек» либо наоборот. При прочих равных выражать лучше то, чтобы выгоднее была подстановка. Привлекательней выглядит подстановка во 2-е уравнение, а посему выражаем «игрек» ![]() и подставляем его в оное:
и подставляем его в оное:
![]() , после чего 2-е уравнение удобно сразу возвести в квадрат:
, после чего 2-е уравнение удобно сразу возвести в квадрат:
![]()
Теперь нужно исключить переменную «икс», для этого из 1-го уравнения выразим:
![]() – подставляем во 2-е уравнение:
– подставляем во 2-е уравнение:
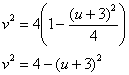
![]() – окружность с центром в точке
– окружность с центром в точке ![]() , радиуса 2.
, радиуса 2.
Таким образом, окружность ![]() отобразилась в окружность
отобразилась в окружность ![]() (коричневый цвет на чертеже).
(коричневый цвет на чертеже).
Решение можно упростить, рассмотрев параметрическое уравнение окружности ![]() :
:
![]()
В этом случае нужно составить систему ![]() и, исключив параметр «тэ», получить то же уравнение
и, исключив параметр «тэ», получить то же уравнение ![]() плоскости
плоскости ![]() . Это рабочие формулы (2) для параметрически заданной линии
. Это рабочие формулы (2) для параметрически заданной линии ![]() , добавьте их в свой справочник.
, добавьте их в свой справочник.
В нашей задаче:
![]() – и уже здесь опытный глаз сможет определить тип линии. Уравнения
– и уже здесь опытный глаз сможет определить тип линии. Уравнения ![]() задают окружность радиуса 2 с центром в начале координат, но по первой координате у нас есть вычитание тройки, что означает сдвиг графика на 3 единицы влево.
задают окружность радиуса 2 с центром в начале координат, но по первой координате у нас есть вычитание тройки, что означает сдвиг графика на 3 единицы влево.
Аналитически результат можно получить с помощью основного тригонометрического тождества ![]() , из которого выгоднее выразить синус
, из которого выгоднее выразить синус ![]() и подставить его во 2-е уравнение системы:
и подставить его во 2-е уравнение системы:
![]()
Далее по аналогии с первым способом решения возводим 2-е уравнение в квадрат:
![]() , из 1-го уравнения выражаем косинус
, из 1-го уравнения выражаем косинус ![]() и подставляем его во 2-е уравнение:
и подставляем его во 2-е уравнение:
![]() , получив тот же самый результат
, получив тот же самый результат ![]() .
.
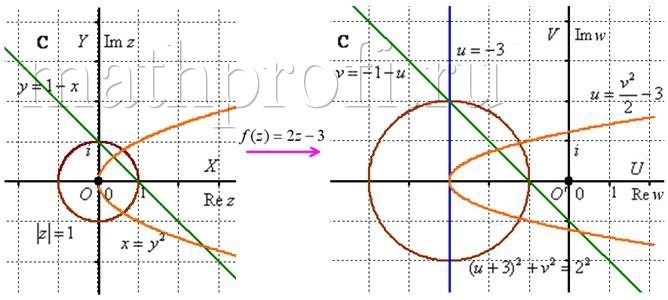
Ответ: а) ось ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]()
Скорее всего, у вас сложилось впечатление, что линия обязательно отображается в однотипную линию (прямая в прямую, окружность в окружность и т. д.). Разумеется, это не так. В общем случае комплексная функция ![]() запросто отобразит линию – в линию другого типа, прямую в окружность, например, и это ещё самое обыкновенное чудо.
запросто отобразит линию – в линию другого типа, прямую в окружность, например, и это ещё самое обыкновенное чудо.
Следующие примеры для самостоятельного решения, классика жанра:
Пример 2
Отобразить линии 1) ![]() , 2)
, 2) ![]() (составить параметрические уравнения), 3)
(составить параметрические уравнения), 3) ![]() с помощью функции
с помощью функции ![]() .
.
и задание, я бы сказал, повышенной сложности:
Пример 3
Найти образы координатных осей ![]() при отображении
при отображении ![]()
Здесь удобно использовать параметрические уравнения. При отображении оси ![]() следует иметь в виду, что точка
следует иметь в виду, что точка ![]() не входит в область определения функции. РассмотрИте два участка оси и проанализируйте, во что они отображаются при изменении параметра «тэ», продвинутые читатели могут использовать односторонние пределы, которые мы активно эксплуатировали при нахождении несобственных интегралов второго рода.
не входит в область определения функции. РассмотрИте два участка оси и проанализируйте, во что они отображаются при изменении параметра «тэ», продвинутые читатели могут использовать односторонние пределы, которые мы активно эксплуатировали при нахождении несобственных интегралов второго рода.
Решаем, сверяемся с образцом внизу страницы и переходим к отображению областей. В классической учебной задаче область ограничена несколькими линиями:
Пример 4
Отобразить область ![]() с помощью функции
с помощью функции ![]() :
:
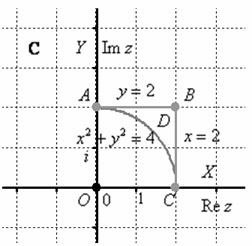
Это всё из ваших контрольных работ, решаем: действительная и мнимая части данной функции уже найдены в Примере 2: ![]() и на первом шаге напрашивается отобразить вершины области:
и на первом шаге напрашивается отобразить вершины области:
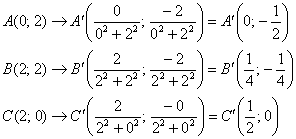
После чего выясняем, во что отобразятся куски границы:
1) Отрезок прямой ![]() между точками
между точками ![]() и
и ![]() .
.
Запишем параметрические уравнения этой прямой: ![]() и подставим их в действительную и мнимую часть функции:
и подставим их в действительную и мнимую часть функции:
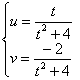 , при этом «тэ» у нас изменятся в пределах
, при этом «тэ» у нас изменятся в пределах ![]() , ибо отрезок.
, ибо отрезок.
Теперь нужно исключить параметр. Из 2-го уравнения выражаем ![]() и ещё сразу выразим «тэ»:
и ещё сразу выразим «тэ»: ![]() . Подставим эти выражения в 1-е уравнение:
. Подставим эти выражения в 1-е уравнение:
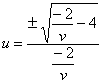
и избавимся от четырёхэтажности дроби:
![]()
возведём обе части в квадрат:
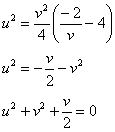
выделим полный квадрат:
![]()
![]()
Таким образом, отрезок ![]() отобразился в дугу окружности с центром в точке
отобразился в дугу окружности с центром в точке ![]() радиуса
радиуса ![]() . Но в какую именно? Ведь точки
. Но в какую именно? Ведь точки ![]() и
и ![]() делят окружность на две дуги. Для прояснения этого вопроса смотрим на пределы изменения параметра
делят окружность на две дуги. Для прояснения этого вопроса смотрим на пределы изменения параметра ![]() , выбираем какое-нибудь промежуточное значение, проще всего взять
, выбираем какое-нибудь промежуточное значение, проще всего взять ![]() , и подставляем его в параметрические уравнения
, и подставляем его в параметрические уравнения ![]() :
:
![]() – в результате получились координаты точки, которая лежит на меньшей дуге – её я обозначил красной линией (см. чертёж ниже).
– в результате получились координаты точки, которая лежит на меньшей дуге – её я обозначил красной линией (см. чертёж ниже).
Да, и, кстати, не лишним будет проверить, что координаты точек ![]() удовлетворяют уравнению
удовлетворяют уравнению ![]() , а то вдруг мы вообще где-то ошиблись?
, а то вдруг мы вообще где-то ошиблись?
2) Отобразим отрезок прямой ![]() между точками
между точками ![]() и
и ![]() .
.
Алгоритм тот же самый. Записываем параметрические уравнения прямой: ![]() и подставляем их в действительную и мнимую часть функции:
и подставляем их в действительную и мнимую часть функции:
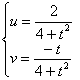 , при этом отрезку
, при этом отрезку ![]() соответствуют тот же диапазон
соответствуют тот же диапазон ![]() .
.
Из 1-го уравнения выражаем ![]() и
и ![]() – подставляем во 2-е уравнение:
– подставляем во 2-е уравнение:
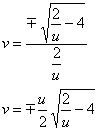
Возводим обе части в квадрат и допиливаем нашу белоснежку:
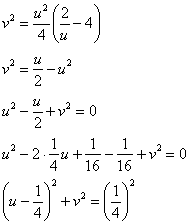
И уже тут лучше сразу устно проверить, что координаты точек ![]() удовлетворяют полученному уравнению.
удовлетворяют полученному уравнению.
Таким образом, отрезок ![]() отобразился в дугу окружности с центром в точке
отобразился в дугу окружности с центром в точке ![]() радиуса
радиуса ![]() . В какую именно дугу? Берём промежуточное значение параметра
. В какую именно дугу? Берём промежуточное значение параметра ![]() , подставляем его в систему выше и выясняем, что получена точка дуги, которую я провёл зелёным цветом (см. чертёж ниже).
, подставляем его в систему выше и выясняем, что получена точка дуги, которую я провёл зелёным цветом (см. чертёж ниже).
3) И, наконец, третье отображение, его мы уже выполнили в Примере 3. Дуга окружности ![]() между точками
между точками ![]() и
и ![]() отображается в дугу окружности
отображается в дугу окружности ![]() между точками
между точками ![]() и
и ![]() (устно проверяем, что координаты точек удовлетворяют уравнению).
(устно проверяем, что координаты точек удовлетворяют уравнению).
Выясним, в какую именно дугу. Запишем параметрические уравнения окружности ![]() :
: ![]() и подставим их в действительную и мнимую части функции:
и подставим их в действительную и мнимую части функции:
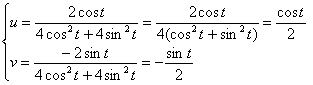
Исходной дуге ![]() , очевидно, соответствуют следующие пределы изменения параметра:
, очевидно, соответствуют следующие пределы изменения параметра: ![]() . Берём какое-нибудь промежуточное значение, например,
. Берём какое-нибудь промежуточное значение, например, ![]() и подставляем его в систему выше:
и подставляем его в систему выше:
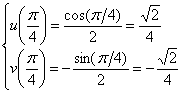 – в результате получились координаты точки, которая лежит именно на той дуге, которую я провёл синим цветом (справа):
– в результате получились координаты точки, которая лежит именно на той дуге, которую я провёл синим цветом (справа):
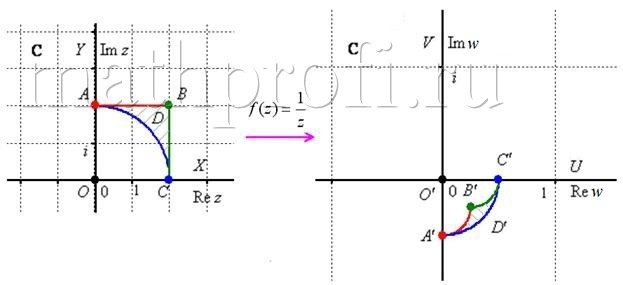
Таким образом, функция ![]() отобразила область
отобразила область ![]() в область
в область ![]() : Вот такая вот птичка получилась.
: Вот такая вот птичка получилась.
Следующее задание для самостоятельного решения:
Пример 5
Отобразить область ![]() с помощью функции
с помощью функции ![]() .
.
И после сверки переходим к следующей теме… – да, они самые!
Решения и ответы:
Пример 2. Решение: найдём действительную и мнимую часть функции ![]() . Так как
. Так как ![]() , то, домножая числитель и знаменатель на сопряжённое знаменателю число, получаем:
, то, домножая числитель и знаменатель на сопряжённое знаменателю число, получаем:
![]()
Таким образом:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() (не теряем «минус»!) – её мнимая часть.
(не теряем «минус»!) – её мнимая часть.
1) Отобразим с помощью функции прямую ![]() . Составим и решим соответствующую систему:
. Составим и решим соответствующую систему:
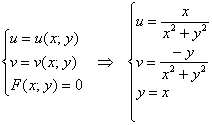 – подставим
– подставим ![]() в первые два уравнения:
в первые два уравнения:
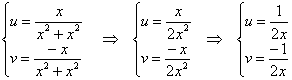 – из 1-го уравнения выразим
– из 1-го уравнения выразим ![]() – подставим во 2-е уравнение и избавимся от трёхэтажности дроби:
– подставим во 2-е уравнение и избавимся от трёхэтажности дроби:
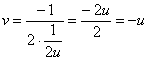
Таким образом, прямая ![]() плоскости
плоскости ![]() отображается в прямую
отображается в прямую ![]() плоскости
плоскости ![]() (см. рис ниже).
(см. рис ниже).
2) Отобразим линию ![]() – луч, исходящий из начала координат и делящий 2-ю координатную четверть пополам, при этом начало исключается, так как для него аргумент не определён. Данный луч лежит на прямой
– луч, исходящий из начала координат и делящий 2-ю координатную четверть пополам, при этом начало исключается, так как для него аргумент не определён. Данный луч лежит на прямой ![]() . Запишем её уравнение в параметрической форме: если
. Запишем её уравнение в параметрической форме: если ![]() , то
, то ![]() , таким образом:
, таким образом: ![]() . При этом лучу
. При этом лучу ![]() соответствуют следующие пределы изменения параметра
соответствуют следующие пределы изменения параметра ![]() : от 0 (не включая ноль) до
: от 0 (не включая ноль) до ![]() , то есть значения параметра убывают.
, то есть значения параметра убывают.
Запишем действительную и мнимую часть функции в параметрической форме ![]() :
:
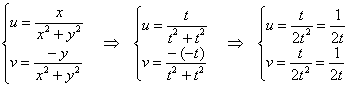 , при этом финальному значению
, при этом финальному значению ![]() соответствует предельная точка
соответствует предельная точка ![]() (начало координат) плоскости
(начало координат) плоскости ![]() , а при
, а при ![]() («тэ» стремится к нулю слева) действительная и мнимая части функции стремятся к «минус» бесконечности:
(«тэ» стремится к нулю слева) действительная и мнимая части функции стремятся к «минус» бесконечности: ![]() . Выясним, вдоль какой линии это всё происходит. Из 1-го уравнения системы выразим
. Выясним, вдоль какой линии это всё происходит. Из 1-го уравнения системы выразим ![]() – подставим во 2-е уравнение:
– подставим во 2-е уравнение: 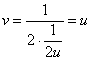 – вдоль прямой
– вдоль прямой ![]() .
.
Таким образом, при изменении параметра ![]() от 0 (не включая ноль) до
от 0 (не включая ноль) до ![]() биссектриса 2-й координатной четверти
биссектриса 2-й координатной четверти ![]() отображается в биссектрису 3-й координатной четверти, проходимой от «минус» бесконечности до нуля (синие линии на чертеже ниже).
отображается в биссектрису 3-й координатной четверти, проходимой от «минус» бесконечности до нуля (синие линии на чертеже ниже).
Примечание: при желании можно рассмотреть возрастающий параметр ![]() , и тогда лучи будут «отрисовываться» в противоположных направлениях.
, и тогда лучи будут «отрисовываться» в противоположных направлениях.
3) Отобразим окружность ![]() , которой соответствует декартово уравнение
, которой соответствует декартово уравнение ![]() . Запишем соответствующую систему:
. Запишем соответствующую систему:
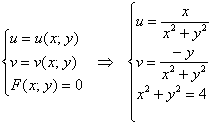 – подставим
– подставим ![]() – в первые два уравнения:
– в первые два уравнения:
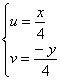 и оба уравнения удобно сразу возвести в квадрат:
и оба уравнения удобно сразу возвести в квадрат: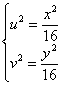 .
.
Из уравения окружности выразим ![]() – подставим в 1-е уравнение:
– подставим в 1-е уравнение:
![]() , откуда выразим «игрек квадрат»:
, откуда выразим «игрек квадрат»:
![]()
![]() – и подставим его во 2-е уравнение:
– и подставим его во 2-е уравнение:
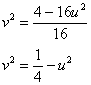
Таким образом, окружность ![]() отобразилась в окружность
отобразилась в окружность ![]() (коричневые линии на чертеже).
(коричневые линии на чертеже).
Ответ: 1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() .
.
Пример 3. Решение: так как ![]() , то
, то ![]()
а) Запишем параметрические уравнения оси ![]() и подставим их в функцию:
и подставим их в функцию:
![]()
1) Рассмотрим участок ![]() . Предельному значению
. Предельному значению ![]() соответствует точка:
соответствует точка:
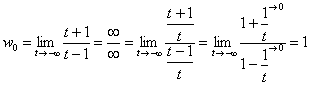 – лежащая на оси
– лежащая на оси ![]() .
.
А если мы приближаемся к единице слева, то ![]() .
.
Таким образом, участок оси ![]() от
от ![]() до
до ![]() отображается в аналогичный участок оси
отображается в аналогичный участок оси ![]() , проходимый (внимание!) справа налево от
, проходимый (внимание!) справа налево от ![]() (не включая точку) до «минус» бесконечности.
(не включая точку) до «минус» бесконечности.
2) Рассмотрим участок ![]() . Вблизи единицы справа ситуация такова:
. Вблизи единицы справа ситуация такова:
![]()
Предельному значению ![]() соответствует та же точка
соответствует та же точка ![]() .
.
Таким образом, участок оси ![]() от
от ![]() до
до ![]() отображается в аналогичный участок оси
отображается в аналогичный участок оси ![]() , проходимый справа налево от «плюс» бесконечности до точки
, проходимый справа налево от «плюс» бесконечности до точки ![]() (точка исключается).
(точка исключается).
б) Запишем параметрические уравнения оси ![]() и подставим их в функцию:
и подставим их в функцию:
![]()
Умножим числитель и знаменатель на сопряженное знаменателю число:
![]()
Составим систему из действительно и мнимой частей функции:
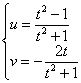
Преобразуем первое уравнение: ![]() и выразим из него:
и выразим из него:
![]() и, кроме того, ещё нужно выразить «тэ»:
и, кроме того, ещё нужно выразить «тэ»:
![]()
Подставим ![]() и
и ![]() во 2-е уравнение системы:
во 2-е уравнение системы:
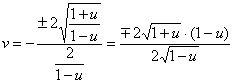
сокращаем числитель и знаменатель на двойку и на ![]() :
:
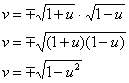
и возводим обе части в квадрат:
![]()
Таким образом, ось ![]() отобразилась в единичную окружность
отобразилась в единичную окружность ![]() плоскости
плоскости ![]() .
.
Ответ: а) ось ![]() , проходимая от точки
, проходимая от точки ![]() до
до ![]() и от
и от ![]() до той же точки (точка исключается), б)
до той же точки (точка исключается), б) ![]() .
.
Пример 5. Решение: найдём действительную и мнимую часть функции ![]() . Так как
. Так как ![]() , то:
, то:
![]()
Таким образом:
![]()
Область ![]() ограничена дугой окружности
ограничена дугой окружности ![]() сверху и прямой
сверху и прямой ![]() снизу (см. рис. ниже). Найдём координаты вершин области:
снизу (см. рис. ниже). Найдём координаты вершин области: 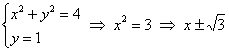 и отобразим их с помощью функции
и отобразим их с помощью функции ![]() :
:
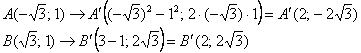
1) Отобразим отрезок ![]() . Запишем параметрические уравнения прямой
. Запишем параметрические уравнения прямой ![]() и подставим их в действительную и мнимую часть функции:
и подставим их в действительную и мнимую часть функции:
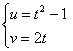 , при этом
, при этом ![]() .
.
Из 2-го уравнения выразим ![]() – подставим в 1-е уравнение:
– подставим в 1-е уравнение:
![]() – парабола с вершиной в точке
– парабола с вершиной в точке ![]() и ветвями по направлению оси
и ветвями по направлению оси ![]() .
.
Таким образом, отрезок ![]() , очевидно, отобразился во фрагмент параболы
, очевидно, отобразился во фрагмент параболы ![]() между точками
между точками ![]() (проверяем, что координаты удовлетворяют уравнению).
(проверяем, что координаты удовлетворяют уравнению).
2) Отобразим дугу ![]() окружности
окружности ![]() . Запишем её параметрические уравнения:
. Запишем её параметрические уравнения: ![]() и определим пределы изменения параметра. Точке
и определим пределы изменения параметра. Точке ![]() соответствует следующее значение тангенса:
соответствует следующее значение тангенса: ![]() (можно заглянуть в тригонометрическую таблицу). И из соображений симметрии находим конечное значение параметра:
(можно заглянуть в тригонометрическую таблицу). И из соображений симметрии находим конечное значение параметра: ![]() . Таким образом, параметр изменяется в пределах
. Таким образом, параметр изменяется в пределах ![]() .
.
Подставим ![]() в действительную и мнимую часть функции:
в действительную и мнимую часть функции:
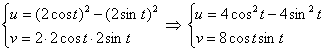
По известным формулам перейдём к двойному аргументу:
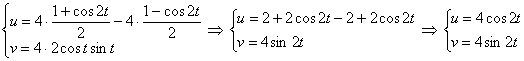 – в результате получены параметрические уравнения окружности
– в результате получены параметрические уравнения окружности ![]() .
.
Таким образом, дуга ![]() окружности
окружности ![]() отобразилась в дугу окружности
отобразилась в дугу окружности ![]() (проверяем, что координаты точек
(проверяем, что координаты точек ![]() удовлетворяют уравнению).
удовлетворяют уравнению).
Выясним, в какую именно дугу. Берём какое-нибудь промежуточное значение из диапазона ![]() , напрашивается
, напрашивается ![]() , и подставляем его в полученные параметрические уравнения
, и подставляем его в полученные параметрические уравнения ![]() :
:
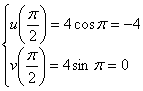 – в результате получены координаты точки, которая лежит на бОльшей (левой) дуге.
– в результате получены координаты точки, которая лежит на бОльшей (левой) дуге.
В результате область ![]() отобразилась в Пакмэна:))
отобразилась в Пакмэна:))
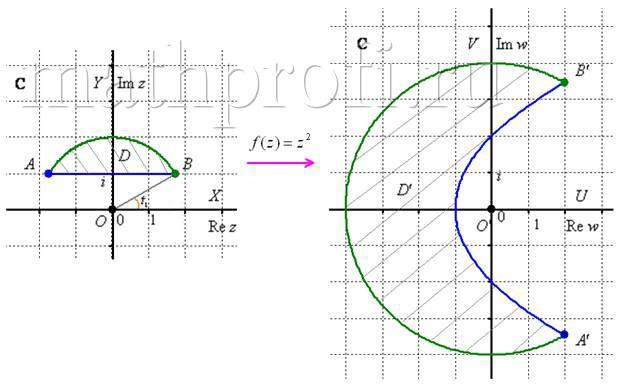
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
