Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Задача с треугольной пирамидой

После пройденного пути, который начался на уроке Векторы для чайников и закончился статьёй Задачи с прямой и плоскостью, рассмотрим распространённое задание, главным действующим героем которого является треугольная пирамида (тетраэдр). Посмотрим на эту пространственную фигуру и перечислим её элементарные признаки:

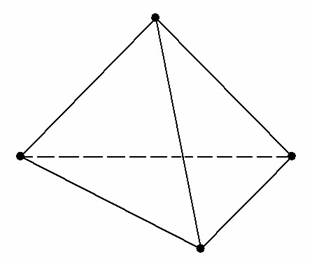
У треугольной пирамиды есть:

– четыре вершины;
– шесть рёбер (сторон);
– четыре грани.

Чем богаты, тем и рады. Каждая из четырёх граней представляет собой треугольник, отсюда и название – треугольная пирамида или тетраэдр.

Не буду перечислять геометрические свойства данной фигуры, известные из школьной программы, поскольку аналитическая геометрия вскрывает пакет молока своим способом. А именно, пристальное внимание уделяется уравнениям рёбер, плоскостей, всевозможным углам пирамиды и некоторым другим вещам, скоро увидите.

Примечание: корректнее говорить «уравнения прямой, содержащей ребро (стОрону)» и «уравнение плоскости, содержащей грань». Но для краткости будем использовать словосочетания «уравнения ребра (сторонЫ)» и «уравнение грани».

Особых трудностей не ожидается, так как весь инструментарий базируется на уже изученных материалах. Но если где-то обнаружатся пробелы, ничего страшного, каждый пункт решения будет снабжён ссылками на нужные уроки, чайник пыхтит – задача решается =)

Кроме того, мы поэтапно выполним точный чертёж пирамиды в прямоугольной системе координат. Это очень важный шаг для тех, кто только начинает разбираться с трёхмерными чертежами.

Приключения с треугольной пирамидой концептуально напоминают задачу с треугольником на плоскости. И начинаются они примерно так:

Треугольная пирамида задана координатами своих вершин

Далее, как правило, вам предложат четыре точки пространства. Причём, прямо сейчас =)

Пусть это будут вершины .

Требуется:

Потребуется много чего…. Счастливчики отделаются 3-4 пунктами, а билет с крупным выигрышем может насчитывать добрый десяток заданий.

Поздравляю, вы сорвали Джекпот!

1) найти длину ребра ;

2) составить уравнения стороны ;

3) найти угол между рёбрами ;

4) найти площадь грани ;

5) найти угол между ребром  и плоскостью ;

6) составить уравнение грани ;

7) составить уравнения высоты , опущенной из вершины  на грань ;

8) вычислить длину высоты ;

9) найти основание высоты ;

10) вычислить объем пирамиды;

11) составить уравнения медианы  грани ;

12) составить уравнение плоскости, проходящей через прямую  и вершину ;

13) найти угол между плоскостями  и ;

14) выполнить чертёж пирамиды  в прямоугольной декартовой системе координат;

15) перекреститься левой пяткой.

Это единственная задача данного урока, и вот так, слегка креативно, я решил записать условие... …немного наскучило выстраивать вереницу Пример 1, Пример 2, Пример 3, ….

Начнём-с бренчать монетами по карманам.

Во-первых, разберёмся с обозначениями вершин. Самый распространённый вариант, когда они обозначены буквами . Выполним схематический чертёж:

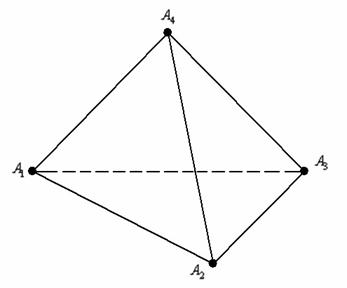
Если бегло просмотреть пункты задачи, то легко заметить, что в условии часто встречается грань . Чаще всего требуется составить уравнение этой «особенной» грани, а также найти её площадь. В качестве «особенной» вершины выступает точка , обычно из неё строится перпендикуляр к плоскости .

А всё это я сказал к тому, что в вашей задаче могут быть совершенно другие обозначения вершин. Например, . При таких буквах «особенной» гранью, скорее всего, будет грань , а «особенной» точкой – вершина . В этой связи очень важно выполнить схематический рисунок пирамиды, чтобы не запутаться в дальнейшем алгоритме решение. Да, более подготовленные читатели могут представлять тетраэдр мысленно, но для чайников чертёж просто обязателен.

Итак, на предварительном этапе разбираемся с обозначениями вершин пирамиды, анализируем условие, находим «нужную» плоскость и точку, выполняем бесхитростный набросок на черновике.

С чего начать решение задачи?

Перед тем, как отправиться в весёлое путешествие по пунктам условия, удобно найти три вектора. Почти всегда векторы откладываются от первой вершины, в данном случае – от точки . Решим элементарную задачу урока Векторы для чайников:

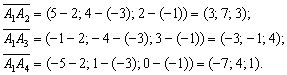
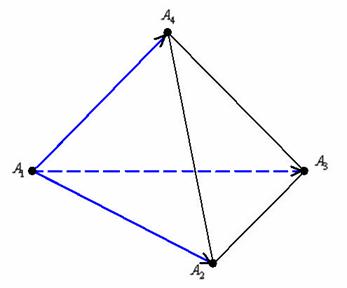
Элементарность элементарностью, но многие давно заметили, что эти простые вычисления на самом деле… достаточно неприятны! Дело в том, у каждого из нас бывает наваждение а-ля «два плюс два равно пяти», поэтому лучше подстраховаться и воспользоваться программой, которая заранее обсчитает многие параметры пирамиды. Калькулятор можно найти на странице Математические формулы и таблицы.

Кроме того, чтобы эффективнее и КОМФОРТНЕЕ воспринимать информацию, координаты четырёх точек и трёх полученных векторов рекомендую переписать на бумагу.

Как найти длину ребра пирамиды?

1) Найдём длину ребра . Длина данного ребра равна длине вектора :

Я обычно округляю результаты до двух знаков после запятой, но в условии задачи может быть дополнительное указание проводить округления, например, до 1-го или 3-го десятичного знака.

Думаю, в случае необходимости никого не затруднит аналогичным образом найти длины рёбер   или . Если же вам предложено найти длину какой-нибудь другой стороны, то используйте формулу нахождения длины отрезка по двум точкам:

Это всё простейшие задачи первого урока про векторы.

Как составить уравнения стороны пирамиды?

2) Найдём уравнения ребра . Очевидно, что речь идёт об уравнениях прямой в пространстве, но нам не сказано, в каком виде их нужно составить. «По умолчанию» обычно подразумевается, что студент запишет канонические уравнения прямой.

Уравнения ребра  составим по точке  (можно взять ) и направляющему вектору :

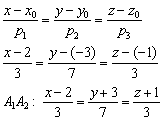
В целях проверки следует убедиться, что обе точки удовлетворяют найденным уравнениям.

Как найти угол между рёбрами пирамиды?

3) Найдём угол между сторонами :

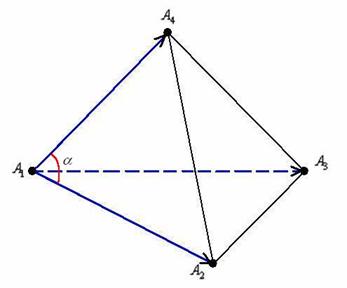
Перед вами обычный угол пространственного треугольника, который рассчитывается как угол  между векторами. И снова при делах тривиальная формула урока Скалярное произведение векторов:

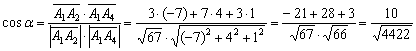
Заметьте, что в ходе решения можно (и нужно) использовать полученные ранее результаты, в данном случае нам уже известно, что  (см. пункт 1).

С помощью обратной функции находим сам угол:

Как найти площадь грани пирамиды?

4) Найдём площадь грани :

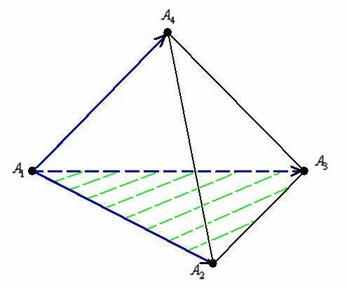
Площадь треугольника вычислим с помощью векторного произведения векторов, используя формулу .

Сначала найдём векторное произведение:

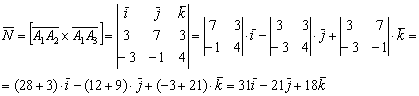
И вычислим его длину:

Вынести из-под корня ничего нельзя, поэтому он войдёт в ответ в неизменном виде.

Площадь грани :

Если получаются страшноватые числа, не обращайте внимания, обычная картина. Главное, не допустить ошибку в вычислениях.

Как найти угол между ребром и гранью?

5) Найдём угол  между ребром  и плоскостью . Это стандартная задача, рассмотренная в Примере № 3 п. «д» урока Основные задачи на прямую и плоскость. Прошу прощения за неточности ряда последующих чертежей, я рисую от руки, отражая лишь принципиальную картину:

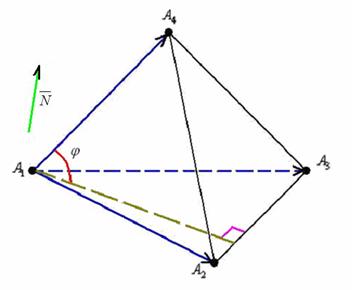
Используем формулу:

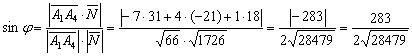
И с помощью арксинуса рассчитываем угол:

Как найти уравнение грани?

6) Составим уравнение плоскости . Первая мысль – использовать точки , но есть более выгодное решение. У нас уже найден вектор нормали  плоскости . Поэтому уравнение грани  составим по точке  (можно взять  либо ) и вектору нормали :

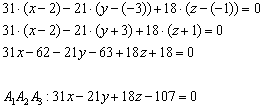
Для проверки можно подставить координаты точек  в полученное уравнение, все три точки должны «подходить».

Как составить уравнения высоты пирамиды?

7) Звучит грозно, решается просто.

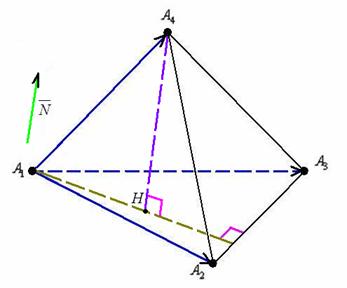
Уравнения высоты , опущенной из вершины  на грань , составим по точке  и направляющему вектору :

 – по умолчанию записываем канонические уравнения.

Вектор нормали в рассматриваемой задаче работает на всю катушку, и как только вам предложили найти площадь грани, составить уравнение грани или уравнения высоты – сразу пробивайте векторное произведение.

Как найти длину высоты пирамиды?

8) Пример № 9 статьи Уравнение плоскости. Длину высоты  найдём как расстояние от точки  до плоскости :

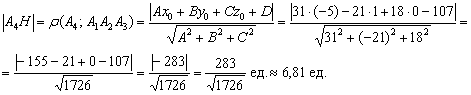
Результат громоздкий, поэтому позволим себе вольность не избавляться от иррациональности в знаменателе.

Как найти основание высоты пирамиды?

9) Найдём основание высоты . Тема пересечения прямой и плоскости подробно муссировалась на уроке Задачи с прямой и плоскостью. Повторим. Перепишем уравнения высоты в параметрической форме:

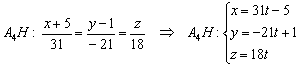
Неизвестным координатам точки  соответствует вполне конкретное значение параметра :
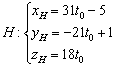, или: .

Основание высоты, понятно, лежит в плоскости. Подставим параметрические координаты точки  в уравнение :


 

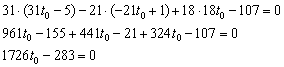
Кому-то покажется жестью, но я ничего не придумал – такое задание с зубодробительными дробями время от времени встречается на практике.

Полученное значение параметра подставим в координаты нашей точки:

Сурово, но идеально точно. Я проверил.

Как найти объем треугольной пирамиды?

10) Старая добрая задача. В аналитической геометрии объем пирамиды традиционно рассчитывается с помощью смешанного произведения векторов:

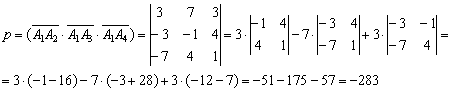
Таким образом:

В данном случае уместно выполнить проверку, вычислив объем тетраэдра по школьной формуле , где  – площадь грани,  – длина высоты, опущенной к этой грани.

Уместно ПОТОМУ, что мы знаем и площадь грани , и длину соответствующей высоты

Как составить уравнения медианы грани пирамиды?

11) Составим уравнения медианы  грани . Ничего сложного, обычная медиана обычного пространственного треугольника:

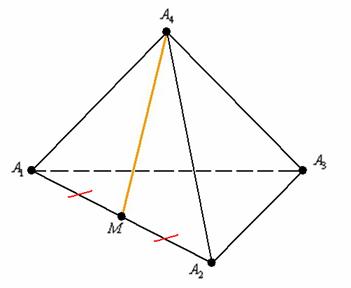
По сравнению с треугольником на плоскости, добавится лишь дополнительная координата. Нам известны вершины , и, по формулам координат середины отрезка, находим реквизиты точки :

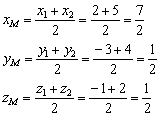
Уравнения медианы можно составить по двум точкам, но в статье Уравнения прямой в пространстве, по некоторым причинам я не рекомендовал использовать такой способ. Поэтому сначала найдём направляющий вектор прямой:

За направляющий вектор можно взять любой коллинеарный вектор, и сейчас подходящий момент избавиться от дробей:

Уравнения медианы составим по точке  и направляющему вектору :

Заметьте, что уравнения с эстетической точки зрения лучше составить по точке , так как координаты точки «эм» – дробные.

Проверка рутинна, нужно подставить координаты точек  в полученные канонические уравнения.

Как составить уравнение плоскости, проходящей через вершину и ребро?

12) Составим уравнение плоскости, проходящей через прямую  и вершину :

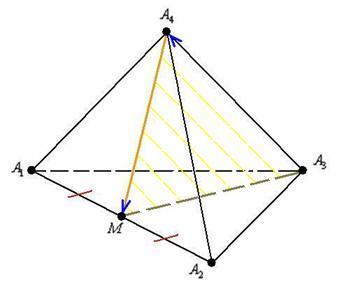
А задаёт ли вообще прямая и не принадлежащая ей точка плоскость? Да, это «жёсткая конструкция», однозначно определяющая плоскость.

К сожалению, мы не знаем вкусный нормальный вектор плоскости , и самый короткий путь – составить уравнение плоскости по точке и двум неколлинеарным векторам.

В качестве точки обязательно выбираем «одинокую» точку, которая не принадлежит прямой, в данном случае – это вершина . Один из нужных векторов уже известен: , но, конечно же, удобнее выбрать его брата-мажора . В качестве второго вектора подходит  либо  (и вообще, бесконечно много векторов, но у нас есть только две «готовые» точки прямой ). Учитывая дробные координаты точки «эм», выгоднее найти:

Уравнение плоскости составим по точке  и двум неколлинеарным векторам :

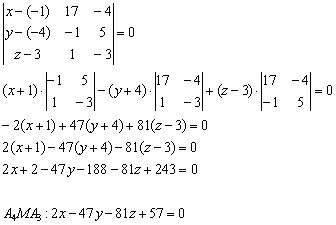
Очевидно, что координаты точек  должны «подходить» в полученное уравнение плоскости.

Как найти угол между гранью и плоскостью?

13) Найдём угол между плоскостями  и .

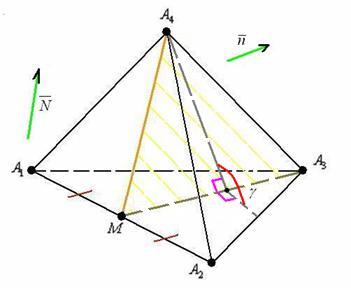
Очередной типовик, рассмотренный в Примере № 13 урока Уравнение плоскости.

Данные плоскости пересекаются, и косинус угла  между ними выражается формулой: 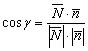, где  – вектор нормали плоскости . Напоминаю, что вектор нормали  и его длина  уже известны.

Осталось снять вектор нормали:  и аккуратно провести вычисления:

Возиться с такими корнями смысла нет, поэтому сразу находим угол:

От тупизны подальше за ответ таки лучше принять острого соседа:

Как начертить пирамиду в прямоугольной системе координат?

14) Выполним точный чертёж пирамиды  прямоугольной системе координат. Это проще, чем кажется.

С чего начать?

Во-первых, необходимо уметь правильно изображать саму систему координат на клетчатой бумаге. Справка в начале методички Графики и свойства функций.

Во-вторых, необходимо уметь строить точки в трёхмерном пространстве, об этом я уже начал рассказывать в статье Уравнения прямой в пространстве. И сейчас мы продолжим тему.

Построим точку . На мой взгляд, сначала удобно разобраться с первыми двумя координатами – «иксом» и «игреком»: отмеряем 2 единицы в положительном направлении оси  и 3 единицы в отрицательном направлении оси . В плоскости  прочерчиваем пунктирные дорожки, которые параллельны соответствующим  координатным осям. Пересечение дорожек я пометил небольшим ромбиком:

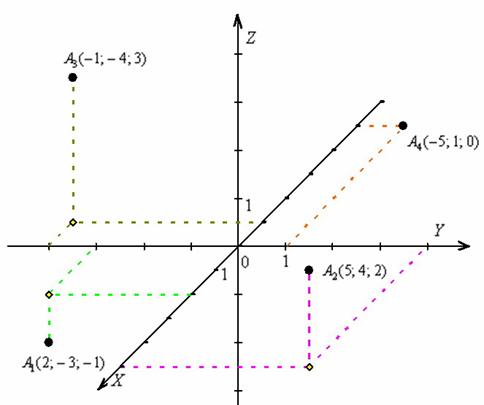
Теперь, в соответствии с отрицательной «зетовой» координатой, отмеряем 1 единицу вниз и тоже проводим пунктирную дорожку. Здесь и будет находиться наша точка , она расположена в нижнем полупространстве.

Для точки  отмеряем 5 единиц «на себя» и 4 единицы вправо, строим параллельные осям пунктирные дорожки и находим их точку пересечения. В соответствии с «зетовой» координатой, чертим пунктиром «подставку для точки» – 2 единицы вверх. Данная точка расположена в верхнем полупространстве.

Аналогично строятся две другие точки. Заметьте, что вершина  лежит в самой плоскости .

В тетради пунктирные линии аккуратно и не жирно проводятся простым карандашом.

Теперь нужно разобраться в удалённости точек, а в этом как раз и помогут пунктирные линии. Немного включаем пространственное воображение и внимательно смотрим на ось . Очевидно, что самая близкая к нам вершина – , а самая удалённая – .

Немало читателей уже мысленно прорисовали пирамиду, тем не менее, остановлюсь на построении подробнее. После того, как построены вершины, чайники могут тонко-тонко карандашом начертить все 6 сторон, и начинать разбираться, какие рёбра видимы, а какие рёбра скрыты. Лучше начать от самой близкой точки . Очевидно, что все три «исходящих» ребра в поле нашего зрения:

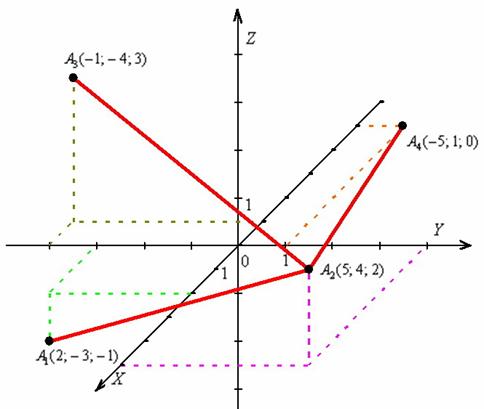
Должен предостеречь, так бывает далеко не всегда, одно ребро, например, может быть от нас скрыто. Не теряйте визуального восприятия пространства!

Какие ещё стороны в зоне видимости? ВиднЫ рёбра , а вот сторона  спряталась за пирамидой:

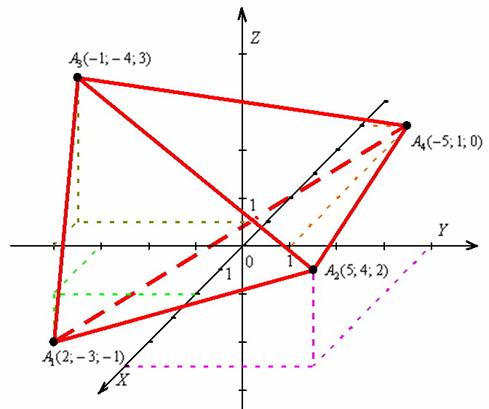
К слову, невидимое нам ребро  лежит в нижнем полупространстве и проходит под осями .

Чертеж-конфетка на практике получается не во всех случаях. Бывает, фортуна разворачивается и задом:

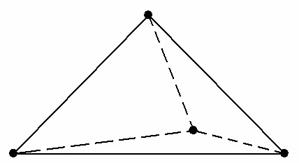
То есть, грань пирамиды может полностью или частично закрывать всё остальное. Но самое скверное, когда перекрываются рёбра:
 
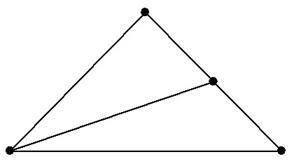
Тут сразу три ребра выстроились на одной прямой (правая верхняя прямая). В похожей ситуации приходится жирно прочерчивать накладывающиеся стороны разными цветами и ниже чертежа записывать дополнительные комментарии о расположении пирамиды.

Существуют и более мелкие неприятности, например, одна из сторон пирамиды может наложиться на координатную ось (а то и вовсе расположиться за ней).

Увы, перечисленные случаи – не редкость на практике.

Вот, пожалуй, и все основные сведения о построении треугольной пирамиды в декартовой системе координат.

15) Это пример для самостоятельного решения.

В конце решения желательно остограммиться записать ответ, и по пунктам перечислить полученные результаты. За ваше здоровье!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте