
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Числовая последовательность.
Как найти предел последовательности?
На данном уроке мы узнаем много интересного из жизни участников большого сообщества под названием Вконтакте числовые последовательности. Рассматриваемая тема относится не только к курсу математического анализа, но и затрагивает основы дискретной математики. Кроме того, материал потребуется для освоения других разделов вышки, в частности, в ходе изучения числовых рядов и функциональных рядов. Можно банально сказать, что это важно, можно ободряюще сказать, что это просто, можно сказать ещё много дежурных фраз, однако сегодня первая, необыкновенно ленивая учебная неделя, поэтому меня жутко ломает сочинять первый абзац =) Уже в сердцАх сохранил файл и собрался спать, как вдруг… голову озарила идея чистосердечного признания, которое невероятно облегчило душу и подтолкнуло к дальнейшему стуку пальцами по клавиатуре.
Отвлечёмся от летних воспоминаний, и заглянем в этот увлекательный и позитивный мир новой социальной сети:
Понятие числовой последовательности
Сначала задумаемся над самим словом: а что такое последовательность? Последовательность – это когда что-то расположено за чем-то. Например, последовательность действий, последовательность времён года. Или когда кто-то расположен за кем-то. Например, последовательность людей в очереди, последовательность слонов на тропе к водопою.
Немедленно проясним характерные признаки последовательности. Во-первых, члены последовательности располагаются строго в определённом порядке. Так, если двух человек в очереди поменять местами, то это уже будет другая последовательность. Во-вторых, каждому члену последовательности можно присвоить порядковый номер:
![]()
С числами всё аналогично. Пусть каждому натуральному значению ![]() по некоторому правилу поставлено в соответствие действительное число
по некоторому правилу поставлено в соответствие действительное число ![]() . Тогда говорят, что задана числовая последовательность
. Тогда говорят, что задана числовая последовательность ![]() .
.
Да, в математических задачах в отличие от жизненных ситуаций последовательность почти всегда содержит бесконечно много чисел.
При этом:
![]() называют первым членом последовательности;
называют первым членом последовательности;
![]() – вторым членом последовательности;
– вторым членом последовательности;
![]() – третьим членом последовательности;
– третьим членом последовательности;
…
![]() – энным или общим членом последовательности;
– энным или общим членом последовательности;
…
На практике последовательность обычно задаётся формулой общего члена, например:
![]() – последовательность положительных чётных чисел:
– последовательность положительных чётных чисел:
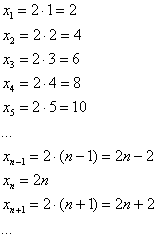
Таким образом, запись ![]() однозначно определяет все члены последовательности – это и есть то правило (формула), по которому натуральным значениям
однозначно определяет все члены последовательности – это и есть то правило (формула), по которому натуральным значениям ![]() в соответствие ставятся числа
в соответствие ставятся числа ![]() . Поэтому последовательность часто коротко обозначают общим членом, причём вместо «икс» могут использоваться другие латинские буквы, например:
. Поэтому последовательность часто коротко обозначают общим членом, причём вместо «икс» могут использоваться другие латинские буквы, например:
Последовательность положительных нечётных чисел ![]() :
:
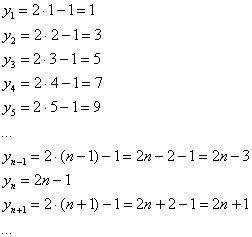
Ещё одна распространённая последовательность ![]() :
:
![]()
Как, наверное, многие подметили, переменная «эн» играет роль своеобразного счётчика.
На самом деле с числовыми последовательностями мы имели дело ещё в средних классах школы. Вспомним арифметическую прогрессию. Определение переписывать не буду, коснёмся самой сути на конкретном примере. Пусть ![]() – первый член, а
– первый член, а ![]() – шаг арифметической прогрессии. Тогда:
– шаг арифметической прогрессии. Тогда:
![]() – второй член данной прогрессии;
– второй член данной прогрессии;
![]() – третий член данной прогрессии;
– третий член данной прогрессии;
![]() – четвертый;
– четвертый;
![]() – пятый;
– пятый;
…
И, очевидно, энный член задаётся рекуррентной формулой ![]()
Примечание: в рекуррентной формуле каждый следующий член выражается через предыдущий член или даже через целое множество предыдущих членов.
Полученная формула малопригодна на практике – чтобы добраться, скажем, до ![]() , нужно перебрать все предыдущие члены. И в математике выведено более удобное выражение энного члена арифметической прогрессии:
, нужно перебрать все предыдущие члены. И в математике выведено более удобное выражение энного члена арифметической прогрессии: ![]() . В нашем случае:
. В нашем случае:
![]()
Подставьте в формулу ![]() натуральные номера
натуральные номера ![]() и проверьте правильность построенной выше числовой последовательности.
и проверьте правильность построенной выше числовой последовательности.
Аналогичные выкладки можно провести для геометрической прогрессии, энный член которой задаётся формулой ![]() , где
, где ![]() – первый член
– первый член ![]() , а
, а ![]() – знаменатель прогрессии
– знаменатель прогрессии ![]() . В заданиях по матану первый член частенько равен единице.
. В заданиях по матану первый член частенько равен единице.
Примеры:
прогрессия ![]() задаёт последовательность
задаёт последовательность ![]() ;
;
прогрессия ![]() задаёт последовательность
задаёт последовательность ![]() ;
;
прогрессия ![]() задаёт последовательность
задаёт последовательность ![]() ;
;
прогрессия ![]() задаёт последовательность
задаёт последовательность ![]() .
.
Надеюсь, все знают, что –1 в нечётной степени равно –1, а в чётной – единице.
Прогрессию называют бесконечно убывающей, если ![]() (последние два случая).
(последние два случая).
Давайте добавим в свой список двух новых друзей, один из которых только что постучался в матрицу монитора:
Последовательность ![]() на математическом жаргоне называют «мигалкой»:
на математическом жаргоне называют «мигалкой»:
![]()
Таким образом, члены последовательности могут повторяться. Так, в рассмотренном примере последовательность состоит из двух бесконечно чередующихся чисел.
А бывает ли так, что последовательность состоит из одинаковых чисел? Конечно. Например, ![]() задаёт бесконечное количество «троек». Для эстетов есть случай, когда в формуле всё же формально фигурирует «эн»:
задаёт бесконечное количество «троек». Для эстетов есть случай, когда в формуле всё же формально фигурирует «эн»: ![]()
Факториал: ![]()
Всего лишь свёрнутая запись произведения:
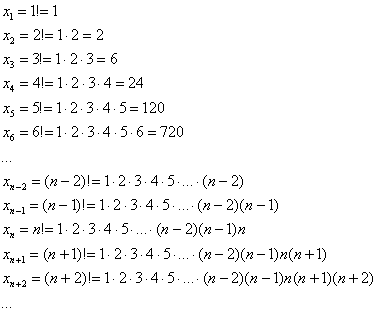
Отнюдь не графомания, пригодится для задач ;-) Рекомендую осмыслить-запомнить и даже переписать в тетрадь. …Пришёл тут в голову один вопрос: а почему никто не создаёт такие полезные граффити? Едет себе человек в поезде, смотрит в окно и изучает факториалы. Панки отдыхают =)
Возможно, некоторым читателям всё-таки ещё не до конца понятно, как расписать члены последовательности, зная общий член. Тот редкий случай, когда контрольный выстрел возвращает к жизни:
Разберёмся с последовательностью ![]() .
.
Сначала подставим в энный член значение ![]() и внимательно проведём вычисления:
и внимательно проведём вычисления:
![]()
Далее подставим в общий член ![]() :
:
![]()
Потом подставим следующий номер ![]() :
:
![]()
Четвёрку:
![]()
Чего уж, теперь и отличную отметку не зазорно заработать:
![]()
и так далее… пока разогреется самый последний чайник!
Понятие предела последовательности. Простейшие примеры
Для лучшего осмысления нижеследующей информации желательно ПОНИМАТЬ, что такое предел функции. Конечно, в стандартном курсе математического анализа сначала рассматривают предел последовательности и только потом предел функции, но дело в том, что о самой сущности предела я уже подробно рассказывал. Более того, в теории числовая последовательность считается частным случаем функции, и людям, которые знакомы с пределом функции, будет заметно веселее.
Впрочем, дальше могут читать все-все-все, однако если у вас возникнет непонимание или недопонимание чего-либо, то, пожалуйста, начните с пределов функций.
Пригласим на танец незамысловатую подругу ![]() :
:
![]()
Что происходит, когда «эн» увеличивается до бесконечности? Очевидно, что члены последовательности будут бесконечно близко приближаться к нулю. Это и есть предел данной последовательности, который записывается следующим образом:
![]()
Если предел последовательности равен нулю, то её называют бесконечно малой.
В теории математического анализа даётся строгое определение предела последовательности через так называемую эпсилон-окрестность. Этому определению будет посвящёна следующая статья, а пока что разберём его смысл:
Изобразим на числовой прямой члены последовательности ![]() и симметричную относительно нуля (предела)
и симметричную относительно нуля (предела) ![]() -окрестность:
-окрестность:
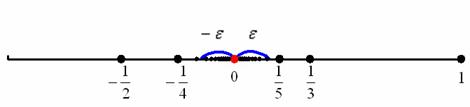
Теперь зажмите синюю окрестность рёбрами ладоней и начинайте её уменьшать, стягивая к пределу (красной точке). Число ![]() является пределом последовательности, если ДЛЯ ЛЮБОЙ заранее выбранной
является пределом последовательности, если ДЛЯ ЛЮБОЙ заранее выбранной ![]() -окрестности (сколь угодно малой) внутри неё окажется бесконечно много членов последовательности, а ВНЕ неё – лишь конечное число членов (либо вообще ни одного). То есть эпсилон-окрестность может быть микроскопической, да и того меньше, но «бесконечный хвост» последовательности рано или поздно обязан полностью зайти в данную окрестность.
-окрестности (сколь угодно малой) внутри неё окажется бесконечно много членов последовательности, а ВНЕ неё – лишь конечное число членов (либо вообще ни одного). То есть эпсилон-окрестность может быть микроскопической, да и того меньше, но «бесконечный хвост» последовательности рано или поздно обязан полностью зайти в данную окрестность.
Есть даже такая задача – доказать предел последовательности, пользуясь определением.
Последовательность ![]() тоже бесконечно малА:
тоже бесконечно малА: ![]() с той разницей, что её члены не прыгают туда-сюда, а подбираются к пределу исключительно справа.
с той разницей, что её члены не прыгают туда-сюда, а подбираются к пределу исключительно справа.
Естественно, предел может быть равен и любому другому конечному числу, элементарный пример:
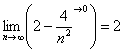
Здесь дробь стремится к нулю, и соответственно, предел равен «двойке».
Если у последовательности ![]() существует конечный предел
существует конечный предел ![]() , то она называется сходящейся (в частности, бесконечно малой при
, то она называется сходящейся (в частности, бесконечно малой при ![]() ). В противном случае – расходящейся, при этом возможны два варианта: либо предела вовсе не существует, либо он бесконечен. В последнем случае последовательность называют бесконечно большой. Пронесёмся галопом по примерам первого параграфа:
). В противном случае – расходящейся, при этом возможны два варианта: либо предела вовсе не существует, либо он бесконечен. В последнем случае последовательность называют бесконечно большой. Пронесёмся галопом по примерам первого параграфа:
Последовательности ![]() являются бесконечно большими, поскольку их члены уверенным ходом продвигаются к «плюс бесконечности»:
являются бесконечно большими, поскольку их члены уверенным ходом продвигаются к «плюс бесконечности»:
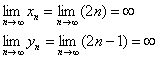
Арифметическая прогрессия с первым членом ![]() и шагом
и шагом ![]() тоже бесконечно великА:
тоже бесконечно великА:
![]()
К слову, расходится и любая арифметическая прогрессия, за исключением случая с нулевым шагом – когда к конкретному числу ![]() бесконечно добавляется
бесконечно добавляется ![]() . Предел такой последовательности существует и совпадает с первым членом.
. Предел такой последовательности существует и совпадает с первым членом.
У последовательностей ![]() схожая судьба:
схожая судьба:
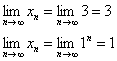
Любая бесконечно убывающая геометрическая прогрессия, как ясно уже из названия, бесконечно малА:
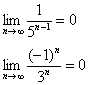
Если знаменатель геометрической прогрессии ![]() , то последовательность бесконечно великА:
, то последовательность бесконечно великА:
![]()
Если же ![]() , например,
, например, ![]() , то предела
, то предела ![]() вообще не существует, так как члены
вообще не существует, так как члены ![]() без устали прыгают то к «плюс бесконечности», то к «минус бесконечности». А здравый смысл и теоремы матана подсказывают, что если что-то куда-то и стремится, то это заветное место единственно.
без устали прыгают то к «плюс бесконечности», то к «минус бесконечности». А здравый смысл и теоремы матана подсказывают, что если что-то куда-то и стремится, то это заветное место единственно.
После небольшого разоблачения ![]() становится понятно, что в безудержных метаниях виновата «мигалка», которая, кстати, расходится и сама по себе.
становится понятно, что в безудержных метаниях виновата «мигалка», которая, кстати, расходится и сама по себе.
Действительно, для последовательности ![]() легко подобрать
легко подобрать ![]() -окрестность, которая, скажем, зажимает только число –1. В результате бесконечное количество членов последовательности («плюс единиц») останутся вне данной окрестности. Но по определению, «бесконечный хвост» последовательности с определённого момента (натурального номера) должен полностью заходить в ЛЮБУЮ
-окрестность, которая, скажем, зажимает только число –1. В результате бесконечное количество членов последовательности («плюс единиц») останутся вне данной окрестности. Но по определению, «бесконечный хвост» последовательности с определённого момента (натурального номера) должен полностью заходить в ЛЮБУЮ ![]() -окрестность своего предела. Вывод: предела
-окрестность своего предела. Вывод: предела ![]() не существует.
не существует.
Факториал ![]() является бесконечно большой последовательностью:
является бесконечно большой последовательностью:
![]()
Причём, растёт он как на дрожжах, так, ![]() представляет собой число, у которого более 100 цифр (разрядов)! Почему именно 70? На нём просит пощады мой инженерный микрокалькулятор.
представляет собой число, у которого более 100 цифр (разрядов)! Почему именно 70? На нём просит пощады мой инженерный микрокалькулятор.
С контрольным выстрелом всё чуть сложнее, и мы как раз подошли к практической части лекции, в которой разберём боевые примеры:
Как найти предел последовательности?
А вот сейчас необходимо уметь решать пределы функций, как минимум, на уровне двух базовых уроков: Пределы. Примеры решений и Замечательные пределы. Потому что многие методы решения будут похожи. Но, прежде всего, проанализируем принципиальные отличия предела последовательности от предела функции:
![]()
В пределе последовательности «динамическая» переменная «эн» может стремиться только к «плюс бесконечности» – в сторону увеличения натуральных номеров ![]() .
.
В пределе функции «икс» может быть направлен куда угодно – к «плюс/минус бесконечности» либо к произвольному действительному числу.
Последовательность дискретна (прерывна), то есть состоит из отдельных изолированных членов. Раз, два, три, четыре, пять, вышел зайчик погулять. Для аргумента же функции характерна непрерывность, то есть «икс» плавно, без приключений стремится к тому или иному значению. И, соответственно, значения функции будут так же непрерывно приближаться к своему пределу.
По причине дискретности в пределах последовательностей встречаются свои фирменные вещи, такие как факториалы, «мигалки», прогрессии и т.п. И сейчас я постараюсь разобрать пределы, которые свойственны именно для последовательностей.
Начнём с прогрессий:
Пример 1
Найти предел последовательности
![]()
Решение: нечто похожее на бесконечно убывающую геометрическую прогрессию, но она ли это? Для ясности распишем несколько первых членов:
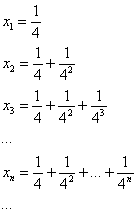
Так как ![]() , то речь идёт о сумме членов бесконечно убывающей геометрической прогрессии, которая рассчитывается по формуле
, то речь идёт о сумме членов бесконечно убывающей геометрической прогрессии, которая рассчитывается по формуле ![]() .
.
Оформляем решение:
![]()
Используем формулу суммы бесконечно убывающей геометрической прогрессии: ![]() . В данном случае:
. В данном случае: ![]() – первый член,
– первый член, ![]() – знаменатель прогрессии.
– знаменатель прогрессии.
Главное, совладать с четырёхэтажностью дроби:
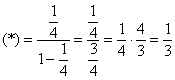
Есть.
Пример 2
Написать первые четыре члена последовательности и найти её предел
![]()
Это пример для самостоятельного решения. Для устранения неопределённости ![]() в числителе потребуется применить формулу суммы
в числителе потребуется применить формулу суммы ![]() первых членов арифметической прогрессии:
первых членов арифметической прогрессии:
![]() , где
, где ![]() – первый, а
– первый, а ![]() – энный член прогрессии.
– энный член прогрессии.
Поскольку в пределах последовательностей «эн» всегда стремится к «плюс бесконечности», то неудивительно, что неопределённость ![]() – одна из самых популярных.
– одна из самых популярных.
И многие примеры решаются точно так же, как пределы функций!
![]()
Как вычислить эти пределы? Смотрите Примеры № 1-3 урока Пределы. Примеры решений.
А может быть что-нибудь посложнее наподобие 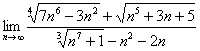 ? Ознакомьтесь с Примером № 3 статьи Методы решения пределов.
? Ознакомьтесь с Примером № 3 статьи Методы решения пределов.
С формальной точки зрения разница будет лишь в одной букве – там «икс», а здесь «эн».
Приём тот же – числитель и знаменатель надо разделить на «эн» в старшей степени.
Также в пределах последовательностей достаточно распространена неопределённость ![]() . Как решать пределы вроде
. Как решать пределы вроде ![]() можно узнать из Примеров № 11-13 той же статьи.
можно узнать из Примеров № 11-13 той же статьи.
Чтобы разобраться с пределом ![]() , обратитесь к Примеру № 7 урока Замечательные пределы (второй замечательный предел справедлив и для дискретного случая). Решение снова будет как под копирку с различием в единственной букве.
, обратитесь к Примеру № 7 урока Замечательные пределы (второй замечательный предел справедлив и для дискретного случая). Решение снова будет как под копирку с различием в единственной букве.
Следующие четыре примера (№ 3-6) тоже «двулики», но на практике почему-то больше характерны для пределов последовательностей, чем для пределов функций:
Пример 3
Найти предел последовательности
![]()
Решение: сначала полное решение, потом пошаговые комментарии:
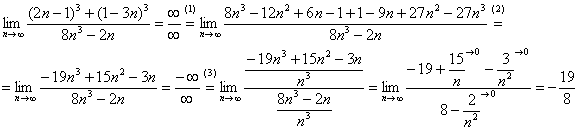
(1) В числителе дважды используем формулу ![]() .
.
(2) Приводим подобные слагаемые в числителе.
(3) Для устранения неопределённости делим числитель и знаменатель на ![]() («эн» в старшей степени).
(«эн» в старшей степени).
Как видите, ничего сложного.
Пример 4
Найти предел последовательности
![]()
Это пример для самостоятельного решения, формулы сокращенного умножения в помощь.
В пределах с показательными последовательностями применяется похожий метод деления числителя и знаменателя:
Пример 5
Найти предел последовательности
![]()
Решение оформим по той же схеме:
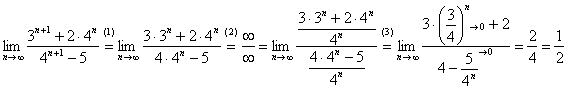
(1) Используя свойства степеней, вынесем из показателей всё лишнее, оставив там только «эн».
(2) Смотрим, какие показательные последовательности есть в пределе: ![]() и выбираем последовательность с наибольшим основанием:
и выбираем последовательность с наибольшим основанием: ![]() . В целях устранения неопределённости делим числитель и знаменатель на
. В целях устранения неопределённости делим числитель и знаменатель на ![]() .
.
(3) В числителе и знаменателе проводим почленное деление. Поскольку ![]() является бесконечно убывающей геометрической прогрессией
является бесконечно убывающей геометрической прогрессией ![]() , то она стремится к нулю. И тем более к нулю стремится константа, делённая на растущую прогрессию:
, то она стремится к нулю. И тем более к нулю стремится константа, делённая на растущую прогрессию: ![]() . Делаем соответствующие пометки и записываем ответ.
. Делаем соответствующие пометки и записываем ответ.
Пример 6
Найти предел последовательности
![]()
Это пример для самостоятельного решения.
Как-то незаслуженно остался в забвении стильный почерк, присущий только пределу последовательности. Пора исправить ситуацию:
Пример 7
Найти предел последовательности
![]()
Решение: чтобы избавиться от «вечного соперника» ![]() нужно расписать факториалы в виде произведений. Но прежде, чем приступить к математическому граффити, рассмотрим конкретный пример, например:
нужно расписать факториалы в виде произведений. Но прежде, чем приступить к математическому граффити, рассмотрим конкретный пример, например: ![]() .
.
Последним множителем в произведении идёт шестёрка. Что нужно сделать, чтобы получить предыдущий множитель? Вычесть единицу: 6 – 1 = 5. Чтобы получить множитель, который располагается ещё дальше, нужно из пятёрки ещё раз вычесть единичку: 5 – 1 = 4. И так далее.
Не беспокойтесь, это не урок в первом классе коррекционной школы, на самом деле мы знакомимся с важным и универсальным алгоритмом под названием «как разложить любой факториал». Давайте разделаемся с самым злостным флудером нашего чата: ![]()
Очевидно, что последним множителем в произведении будет ![]() .
.
Как получить предыдущий множитель? Вычесть единицу: ![]()
Как достать прадедушку? Ещё раз вычесть единицу: ![]() .
.
Ну и ещё на один шаг продвинемся вглубь: ![]()
Таким образом, наше чудовище распишется следующим образом:
![]()
С факториалами числителя всё проще, так, мелкие хулиганы.
Оформляем решение:
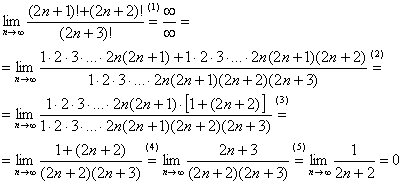
(1) Расписываем факториалы
(2) В числителе ДВА слагаемых. Выносим за скобки всё, что можно вынести, в данном случае это произведение ![]() . Квадратные скобки, как я где-то пару раз говорил, отличаются от круглых скобок только своей квадратностью.
. Квадратные скобки, как я где-то пару раз говорил, отличаются от круглых скобок только своей квадратностью.
(3) Сокращаем числитель и знаменатель на ![]() …. …хммм, флуда тут и впрямь много.
…. …хммм, флуда тут и впрямь много.
(4) Упрощаем числитель
(5) Сокращаем числитель и знаменатель на ![]() . Тут в известной степени повезло. В общем случае вверху и внизу получаются заурядные многочлены, после чего приходится выполнять стандартное действие – делить числитель и знаменатель на «эн» в старшей степени.
. Тут в известной степени повезло. В общем случае вверху и внизу получаются заурядные многочлены, после чего приходится выполнять стандартное действие – делить числитель и знаменатель на «эн» в старшей степени.
Более подготовленные студенты, которые легко раскладывают факториалы в уме, могут решить пример значительно быстрее. На первом шаге делим почленно числитель на знаменатель и мысленно выполняем сокращения:
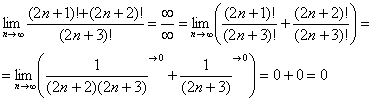
Но способ с разложением всё-таки более основателен и надёжен.
Пример 8
Найти предел последовательности
![]()
Это пример для самостоятельного решения.
Желающие набить руку на рассмотренных типах пределов могут обратиться к сборнику Кузнецова. Около 150 прорешанных примеров можно найти здесь >>> (задачи № 2-6).
Как и в любом обществе, среди числовых последовательностей попадаются экстравагантные личности.
Теорема: произведение ограниченной последовательности на бесконечно малую последовательность – есть бесконечно малая последовательность.
Если вам не очень понятен термин «ограниченность», пожалуйста, изучите статью об элементарных функциях и графиках.
Аналогичная теорема справедлива, кстати, и для функций: произведение ограниченной функции на бесконечно малую функцию – есть бесконечно малая функция.
Пример 9
Найти предел последовательности
![]()
Решение: последовательность ![]() – ограничена:
– ограничена: ![]() , а последовательность
, а последовательность ![]() – бесконечно малА, значит, по соответствующей теореме:
– бесконечно малА, значит, по соответствующей теореме:
![]()
Просто и со вкусом. Да-да, так и оформляем.
А почему бы и нет?
Пример 10
Найти предел последовательности
![]()
Это пример для самостоятельного решения.
Ещё две распространённые ограниченные функции – арктангенс и арккотангенс:
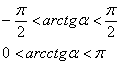
Аргументы перечисленных тригонометрических функций могут быть заполнены знатной абракадаброй, но это не должно приводить в панику – существенно то, что последовательности ограничены!
Иногда в ходе вычисления пределов последовательностей приходится использовать довольно неожиданные приёмы:
Пример 11
Найти предел последовательности
![]()
Решение: неопределённость ![]() можно раскрутить двумя способами. Первый путь – через первый замечательный предел, который справедлив, как ни странно, и для последовательностей:
можно раскрутить двумя способами. Первый путь – через первый замечательный предел, который справедлив, как ни странно, и для последовательностей:
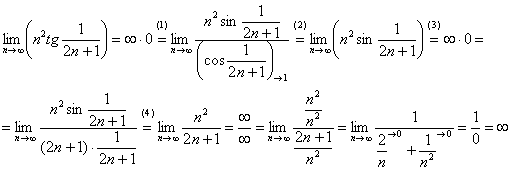
(1) Используем формулу ![]() .
.
(2) Избавляемся от косинуса, указывая, что он стремится к единице.
(3) Неопределённость ![]() не устранена, но теперь вместо тангенса у нас синус, и появляется возможность организовать 1-й замечательный предел. Проводим стандартный искусственный приём: делим всё выражение на
не устранена, но теперь вместо тангенса у нас синус, и появляется возможность организовать 1-й замечательный предел. Проводим стандартный искусственный приём: делим всё выражение на ![]() и, чтобы ничего не изменилось, домножаем на
и, чтобы ничего не изменилось, домножаем на ![]() .
.
(4) Используем первый замечательный предел ![]() , при этом, в качестве бесконечно малой величины выступает
, при этом, в качестве бесконечно малой величины выступает ![]() , которая, понятно, стремится к нулю при
, которая, понятно, стремится к нулю при ![]() .
.
Дальнейшее просто.
Прокатывает и 2-й метод решения – через замечательные эквивалентности:
![]()
Заменим бесконечно малую последовательность эквивалентной:
![]() при
при ![]() .
.
В данном случае ![]()
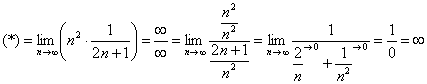
Готово.
Пример 12
Найти предел последовательности
![]()
Это пример для самостоятельного решения. Здесь аргумент арктангенса также бесконечно мал, поскольку его знаменатель более высокого порядка роста, чем числитель. Решать, разумеется, значительно выгоднее через замечательную эквивалентность.
Оба рассмотренных примера справедливы и для функций, похожие пределы также разобраны в Примерах 12-13 урока о бесконечно малых величинах.
В заключение урока рассмотрим ещё один важный вопрос:
Как найти предел знакочередующейся последовательности?
Такая последовательность уже неоднократно встречалась в статье, например, первая скрипка теоретического параграфа ![]() .
.
Действительно, как аналитически найти предел знакочередующейся последовательности, если знак то «плюс», то «минус»?
И я, наконец-то, заряжаю в свой револьвер тот самый волшебный патрон:
Пример 13
Найти предел последовательности ![]()
Решение: на первом шаге следует найти предел последовательности ![]() , которая составлена из модулей членов. Знак модуля уничтожает возможный минус, поэтому чтобы получить
, которая составлена из модулей членов. Знак модуля уничтожает возможный минус, поэтому чтобы получить ![]() , нужно попросту убрать множитель, обеспечивающий знакочередование. Чаще всего это «мигалка»:
, нужно попросту убрать множитель, обеспечивающий знакочередование. Чаще всего это «мигалка»:
![]()
Теперь как ни в чём не бывало, вымучиваем наш обычный предел:
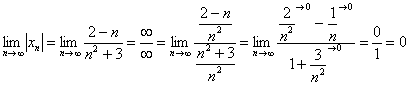
Получено конечное число. Очевидно, что знакочередование не поменяет сути – члены последовательности будут «прыгать» вокруг своего предела, бесконечно близко приближаясь к нему. Собственно, это проиллюстрировано на единственном рисунке данного урока.
Ситуация принципиально такая же, как, например, у более простых последовательностей ![]() .
.
Ответ: так как последовательность является знакочередующейся и ![]() , то
, то ![]() .
.
Если в ходе исследования знакочередующейся последовательности ![]() получен бесконечный результат
получен бесконечный результат ![]() (или если предела нет), то у последовательности
(или если предела нет), то у последовательности ![]() предела не существует вообще. Такой инцидент напоминает историю с
предела не существует вообще. Такой инцидент напоминает историю с ![]() .
.
Наше увлекательное путешествие в мир последовательностей подошло к концу и, надеюсь, оно составило достойную конкуренцию Вконтакте =) =) =)
Успехов в учёбе!
Решения и ответы:
Пример 2: Решение:
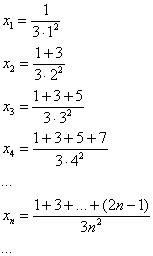
Найдём предел последовательности:
![]()
Используем формулу суммы ![]() первых членов арифметической прогрессии
первых членов арифметической прогрессии ![]() .
.
В данном случае ![]()
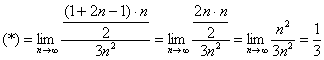
Пример 4: Решение:
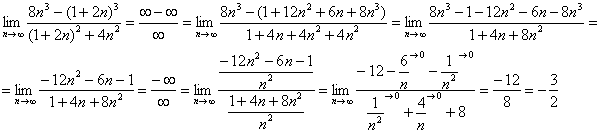
Пример 6: Решение:
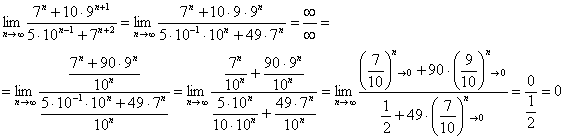
Пример 8: Решение:
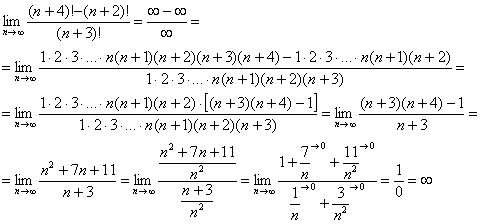
Пример 10: Решение: последовательность ![]() – ограничена:
– ограничена: ![]() , а последовательность
, а последовательность ![]() , значит, по соответствующей теореме:
, значит, по соответствующей теореме:
![]()
Пример 12: Решение:
![]()
Заменим бесконечно малую эквивалентной: ![]() при
при ![]() .
.
В данном примере ![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
