
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Повторные пределы. Примеры решений
Помимо общего предела ![]() функции двух переменных, в некоторых задачах математического анализа рассматриваются так называемые повторные пределы
функции двух переменных, в некоторых задачах математического анализа рассматриваются так называемые повторные пределы ![]() , которым и будет посвящена эта небольшая статья. Что такое повторные пределы? Во-первых, на корню развею распространённое заблуждение начинающих: повторные пределы – это НЕ методы решения общего предела. Общий предел – это общий предел, а повторные пределы – это повторные пределы. Однако между этими понятиями существует взаимосвязь, о которой мы тоже поговорим на сегодняшнем уроке. И в этой связи я рекомендую предварительно изучить пределы функций двух переменных, если вы ещё не успели этого сделать.
, которым и будет посвящена эта небольшая статья. Что такое повторные пределы? Во-первых, на корню развею распространённое заблуждение начинающих: повторные пределы – это НЕ методы решения общего предела. Общий предел – это общий предел, а повторные пределы – это повторные пределы. Однако между этими понятиями существует взаимосвязь, о которой мы тоже поговорим на сегодняшнем уроке. И в этой связи я рекомендую предварительно изучить пределы функций двух переменных, если вы ещё не успели этого сделать.
В целях простоты изложения рассмотрим функцию ![]() , которая непрерывна на всей плоскости
, которая непрерывна на всей плоскости ![]() , за исключением, возможно, точки
, за исключением, возможно, точки ![]() (как вы знаете, понятие предела не требует того, чтобы функция была определена в предельной точке).
(как вы знаете, понятие предела не требует того, чтобы функция была определена в предельной точке).
Теперь задумаемся над записью ![]() и термином «повторный предел». Нетрудно догадаться, что для вычисления такого предела сначала нужно найти
и термином «повторный предел». Нетрудно догадаться, что для вычисления такого предела сначала нужно найти ![]() , а затем уже «внешний» предел от некоего полученного результата. Повторный – один за другим.
, а затем уже «внешний» предел от некоего полученного результата. Повторный – один за другим.
Признаюсь честно, объяснять тяжеловато, поэтому придётся привлечь на помощь не только Фредди, но и его многочисленных друзей =) В добрый путь:
«Внутренний» предел ![]() зависит только от переменной «икс», а значит, при различных значениях «игрек» мы будем бесконечно близко приближаться к прямой
зависит только от переменной «икс», а значит, при различных значениях «игрек» мы будем бесконечно близко приближаться к прямой ![]() в разных местах (чёрные стрелки на чертеже). При этом Фредди и полчища его друзей будут бесконечно близко приближаться по поверхности к голубой кривой:
в разных местах (чёрные стрелки на чертеже). При этом Фредди и полчища его друзей будут бесконечно близко приближаться по поверхности к голубой кривой:
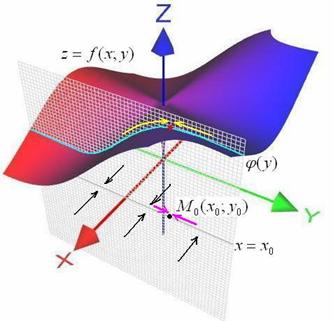
Таким образом, рассматриваемый предел равен не просто числу, а целой функции, которая, очевидно, зависит только от «игрек»:
![]()
Подставим полученный результат во внешний предел:
![]()
Ну а он совсем прост. Стремление ![]() означает, что мы подходим к точке
означает, что мы подходим к точке ![]() по прямой
по прямой ![]() (малиновые стрелки), и соответствующие значения функции приближаются по кривой
(малиновые стрелки), и соответствующие значения функции приближаются по кривой ![]() к красной точке. Пусть она расположена на высоте
к красной точке. Пусть она расположена на высоте ![]() , тогда:
, тогда:
![]()
Таким образом, повторный предел существует и равен ![]() -му:
-му:
![]()
Второй повторный предел ![]() определяется «зеркальным» образом. Если
определяется «зеркальным» образом. Если ![]() , то при различных значениях «икс» мы будет подходить к прямой
, то при различных значениях «икс» мы будет подходить к прямой ![]() в разных местах (чёрные стрелки), и предел
в разных местах (чёрные стрелки), и предел ![]() будет равен функции
будет равен функции ![]() , которая уже зависит только от «икс» (голубая линия на поверхности):
, которая уже зависит только от «икс» (голубая линия на поверхности):
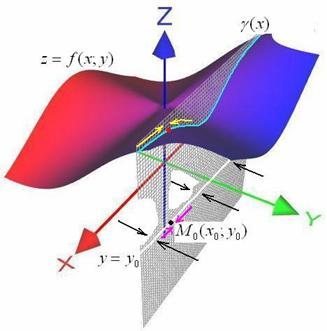
Теперь вычислим ![]() . Стремление
. Стремление ![]() означает, что мы приближаемся к точке
означает, что мы приближаемся к точке ![]() по прямой
по прямой ![]() (малиновые стрелки), и Фредди со своим товарищем в свою очередь приближаются по голубой кривой к той же самой красной точке (жёлтые стрелки):
(малиновые стрелки), и Фредди со своим товарищем в свою очередь приближаются по голубой кривой к той же самой красной точке (жёлтые стрелки): ![]() .
.
Таким образом, второй повторный предел:
![]()
Легко понять, что в точке ![]() существует и общий предел, равный тому же значению:
существует и общий предел, равный тому же значению: ![]() .
.
Однако то был демонстрационный пример, и такая идиллическая картина не должна усыплять бдительность! В общем случае повторные пределы не равны друг другу:
![]()
И, более того, один из них или даже оба могут вовсе не существовать! Согласитесь, не всегда же и не везде можно куда-то подойти.
Освоим технику решения повторных пределов на конкретных примерах:
Пример 1
Найти повторные пределы ![]() для функции
для функции ![]()
Решение удобно разбить на 2 пункта:
1) Вычислим ![]() .
.
Сначала разберёмся с внутренним пределом ![]() . И главный вопрос: что делать с «игреком»? Всё очень просто – с «игреком» нужно временно обращаться, как с константой. По существу, мы решаем обычный предел функции одной переменной, причём его простейший вид:
. И главный вопрос: что делать с «игреком»? Всё очень просто – с «игреком» нужно временно обращаться, как с константой. По существу, мы решаем обычный предел функции одной переменной, причём его простейший вид:
![]()
Подставим полученный результат во внешний предел:
![]()
Таким образом: ![]()
2) Вычислим ![]() .
.
Как и в предыдущем пункте, начинаем с внутреннего предела: ![]() . Теперь временно «замораживается» «икс»:
. Теперь временно «замораживается» «икс»:
![]()
Тут получилось, что «иксы» вообще сократились, и внешний предел становится чистой формальностью, ибо предел любой константы равен самой константе:
![]()
В результате: ![]()
Ответ: ![]()
Пожалуйста, посмотрите на схематический чертёж и постарайтесь ещё раз осмыслить найденные повторные пределы по образцу моих объяснений:
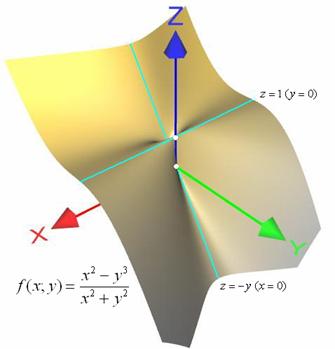
А теперь немного о взаимосвязи с общим пределом: из того, что повторные пределы различны, следует, что общего предела ![]() не существует. Желающие могут убедиться в этом с помощью стандартного алгоритма, рассмотренного на уроке Пределы функций нескольких переменных.
не существует. Желающие могут убедиться в этом с помощью стандартного алгоритма, рассмотренного на уроке Пределы функций нескольких переменных.
Но с другой стороны, если повторные пределы равны, то это ЕЩЁ НЕ ЗНАЧИТ, что существует общий предел. Так, например, для функции ![]() повторные пределы совпадают:
повторные пределы совпадают:
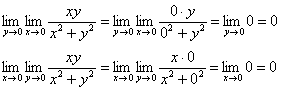
однако в Примере № 1 предыдущего урока мы выяснили, что предела ![]() не существует.
не существует.
Интересно отметить, что если один или оба повторных предела НЕ существуют, то общий предел может существовать! И такой пример будет в конце урока.
А пока разогреваемся:
Пример 2
Найти повторные пределы ![]() , если
, если ![]()
Примерный образец оформления задачи в конце урока.
Фактически мы имеем дело с «обычными» пределами и естественно, что в ходе их решения приходится устранять различные неопределённости:
Пример 3
Вычислить повторные пределы функции ![]() при
при ![]() .
.
Решение: бесконечности, так бесконечности:
1) Вычислим ![]() .
.
Поскольку во внутреннем пределе «динамической» переменной является «икс», то имеет место следующая неопределённость:
![]()
которая раскрывается по классике жанра – делением числителя и знаменателя на «икс» в старшей степени, причём делить можно прямо под синусом. Не забываем, что «игрек» на данном этапе «заморожен»:
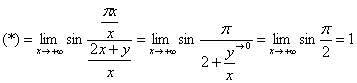 …мда, замёрз в вечной мерзлоте =) Если не очень понятно, почему
…мда, замёрз в вечной мерзлоте =) Если не очень понятно, почему ![]() , мысленно подставьте вместо «игрека» какое-нибудь конкретное число (хотя с содержательной точки зрения, это, конечно, не совсем корректно).
, мысленно подставьте вместо «игрека» какое-нибудь конкретное число (хотя с содержательной точки зрения, это, конечно, не совсем корректно).
И формальная подстановка константы во внешний предел:
![]()
2) Вычислим ![]()
Этот предел ещё проще. Так как роль константы теперь выполняет «икс», то под синусом уже нет неопределённости:
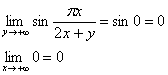
Ответ: ![]()
Самая что ни на есть борода для самостоятельного решения:
Пример 4
Вычислить повторные пределы функции ![]() , если
, если![]() .
.
Краткое решение и ответ в конце урока.
Как видите, ничего особенного, главное, чётко представлять, где и какая переменная находится вне игры. В самих же методах решения какой-то новизны нет:
Пример 5
Найти повторные пределы ![]() , если
, если
![]()
Решение шаблонно:
1) Вычислим ![]()
Во внутреннем пределе вопрос решается прямой подстановкой:
![]()
А вот на завершающем этапе возникают два бублика. Тригонометрическая формула и замечательный предел, думаю, не нуждаются в представлении:
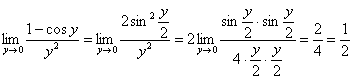
2) Второй повторный предел «симметричен». К слову, когда внутренний предел не слишком наворочен, то решение сподручнее записать «одной строкой»:
![]()
Ответ: ![]()
Два примера для самостоятельного решения. Попроще:
Пример 6
Найти повторные пределы ![]() , если
, если
![]()
И позабористей:
Пример 7
Найти повторные пределы ![]() , если
, если
![]()
Пожалуй, достаточно, ни вижу смысла дублировать материал темы Предел функции одной переменной. Давайте лучше рассмотрим обещанный случай, где оба повторных предела не существуют, но общий таки живёт-здравствует. Хрестоматийный пример, который можно найти во многих источниках информации:
![]()
Для данной функции не существует повторного предела ![]() поскольку, при фиксированном значении «игрек» у множителя
поскольку, при фиксированном значении «игрек» у множителя ![]() нет предела.
нет предела.
Примечание: график функции одной переменной ![]() при
при ![]() «петляет» вдоль оси ординат и бесконечно близко приближается к ней, при этом расстояние между «волнами» синусоиды становиться всё меньше и меньше. Таким образом, предела
«петляет» вдоль оси ординат и бесконечно близко приближается к ней, при этом расстояние между «волнами» синусоиды становиться всё меньше и меньше. Таким образом, предела ![]() не существует. В нашем же примере имеет место пространственный аналог этой ситуации: т.к. значение
не существует. В нашем же примере имеет место пространственный аналог этой ситуации: т.к. значение ![]() может быть любым, то «петлять» будет уже синусоидальная поверхность вдоль плоскости
может быть любым, то «петлять» будет уже синусоидальная поверхность вдоль плоскости ![]() , бесконечно близко приближаясь к ней.
, бесконечно близко приближаясь к ней.
По аналогичной причине не существует и второго повторного предела ![]() . Однако, общий предел всё же существует и равен нулю:
. Однако, общий предел всё же существует и равен нулю:
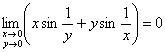
Кстати, не нужно думать, что в этом есть что-то удивительное: если к точке ![]() нет подхода со стороны координатных осей, то это ещё не значит, что к ней нельзя подойти по другим направлениям.
нет подхода со стороны координатных осей, то это ещё не значит, что к ней нельзя подойти по другим направлениям.
И в заключение будет небольшой оффтопик, где я расскажу ещё об одном методе решения предела функции двух переменных. Он основан на так называемой теореме о промежуточном значении. Краткая суть состоит в следующем: если для некоторой функции ![]() удаётся подобрать функцию
удаётся подобрать функцию ![]() – такую, что:
– такую, что:
![]() , то из того, что
, то из того, что ![]() следует, что и
следует, что и ![]() .
.
В рассмотренном примере ввиду ограниченности тригонометрических функций ![]() , для всех «икс» и «игрек» справедливо следующее неравенство:
, для всех «икс» и «игрек» справедливо следующее неравенство:
![]() , и поскольку
, и поскольку ![]() (проверьте это самостоятельно), то
(проверьте это самостоятельно), то 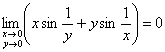 .
.
Данный метод обычно используют, чтобы избавиться от «нехороших» синусов и косинусов, вот ещё один пример такого рода: ![]() .
.
Так как для всех «икс» и «игрек» ![]() , то:
, то: ![]() . А из очевидного предела
. А из очевидного предела ![]() , следует что и наш предел
, следует что и наш предел ![]() .
.
Но иногда сравнение применяют для других функций, докажем, например, предел 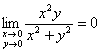 , который мы вычислили в Примере № 2 предыдущего урока «обычным» способом. Альтернативный путь элементарен: дробь
, который мы вычислили в Примере № 2 предыдущего урока «обычным» способом. Альтернативный путь элементарен: дробь ![]() положительна и, кроме того, при любых
положительна и, кроме того, при любых ![]() не превосходит единицы (проанализируйте, почему), поэтому справедливо следующее:
не превосходит единицы (проанализируйте, почему), поэтому справедливо следующее:
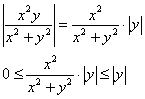
И, так как ![]() , то и
, то и 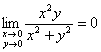 .
.
Просто и корректно! Но, конечно, такую возможность нужно ещё увидеть, и для этого требуется некоторый опыт.
Возвращаясь к теме повторных пределов, сделаем следующий вывод: из существования общего предела ЕЩЁ НЕ СЛЕДУЕТ существование повторных пределов. А о том, что ещё в этом случае нужно для их существования, можно узнать из соответствующей теоремы математического анализа. Формулировки не будет… надо же мне вас чем-то заманивать на страницы учебников по математическому анализу =)
Понятие повторных пределов распространяется и на функции бОльшего количества переменных, но из соображений практической целесообразности я ограничусь рассмотренными примерами.
Спасибо за внимание!
Решения и ответы:
Пример 2: Решение:
1) Вычислим ![]()
![]() – подставим во внешний предел:
– подставим во внешний предел:
![]()
2) Вычислим ![]()
![]() – подставим во внешний предел:
– подставим во внешний предел:
![]()
Ответ: ![]()
Пример 4: Решение:
1) Вычислим ![]()
![]()
Разделим числитель и знаменатель на ![]() :
:
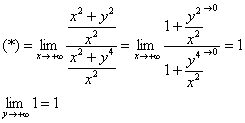
2) Вычислим ![]()
![]()
Разделим числитель и знаменатель на ![]() :
:
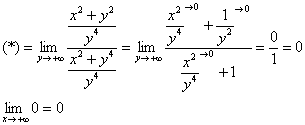
Ответ: ![]()
Пример 6: Решение:
1) ![]()
Заменим бесконечно малую эквивалентной: ![]() при
при ![]()
![]()
2) ![]()
Ответ: ![]()
Пример 7: Решение:
1) Вычислим ![]()
![]()
Используем формулу ![]() и первый замечательный предел:
и первый замечательный предел:
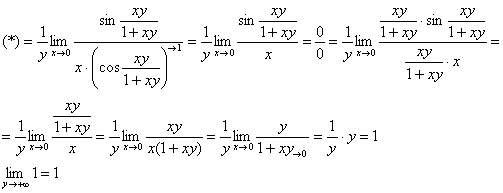
2) Вычислим ![]()
![]()
Разделим числитель и знаменатель аргумента тангенса на ![]() :
:
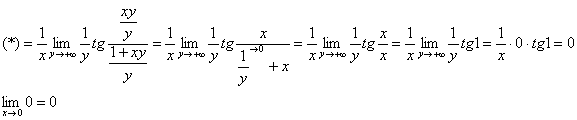
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
