
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Линейные дифференциальные уравнения высших порядков
И снова всех приветствую в разделе «Дифференциальные уравнения», а именно на странице, которая появилась по многочисленным просьбам посетителей сайта. Данная статья является закономерным продолжением уроков об однородных и неоднородных линейных ДУ 2-го порядка, и поэтому нижеследующие материалы эффективнее всего изучать «по горячим следам». Или с уже наработанными навыками решения этих уравнений. Так или иначе, на данный момент у вас должен быть более или менее приличный уровень подготовки по теме.
Наверное, многие уже представляют, как выглядят наши «подопечные». Линейное однородное дифференциальное уравнение ![]() -го порядка имеет следующий вид:
-го порядка имеет следующий вид:
![]()
(напоминаю, что ![]() – это обозначение «энной» производной)
– это обозначение «энной» производной)
и, соответственно, в линейном НЕоднородном дифференциальном уравнении справа присутствует ненулевая функция:
![]()
Достаточно часто названия этих дифуров сокращают до ЛОДУ и ЛНДУ, но я противник излишних аббревиатур. Потому что ЭПСНУУМ =)
Ранее мы рассмотрели линейные ДУ 1-го и 2-го порядков, и сегодня пришло время разделаться с их старшими собратьями, обладающих степенями ![]() . Кроме того, вы узнаете несколько дополнительных приёмов решения неоднородных уравнений 2-го порядка. В большинстве практических примеров коэффициенты
. Кроме того, вы узнаете несколько дополнительных приёмов решения неоднородных уравнений 2-го порядка. В большинстве практических примеров коэффициенты ![]() постоянны (являются константами), однако помимо всего прочего я коснусь и случая, когда там «затесалась» буква «икс». Надеюсь, вам всё очень понравится!
постоянны (являются константами), однако помимо всего прочего я коснусь и случая, когда там «затесалась» буква «икс». Надеюсь, вам всё очень понравится!
Началом этого урока можно смело считать параграф Линейные однородные уравнения высших порядков (откроется на соседней вкладке) вводной статьи, и перед дальнейшим чтением было бы неплохо пробежаться по нему взглядом. …Есть? Собственно, продолжаем:
Пример 1
Найти частное решение дифференциального уравнения ![]() , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям ![]()
Решение: перед нами линейное однородное ДУ 3-го порядка и всё начинается, как уже не раз начиналось. Составим и решим характеристическое уравнение:
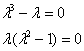
![]() – три различных действительных корня, поэтому общее решение:
– три различных действительных корня, поэтому общее решение:
![]()
Внимание! Если вам НЕ ПОНЯТЕН / ПОЗАБЫЛСЯ принцип формирования общего решения, то, пожалуйста, начните с рекомендованного выше параграфа.
Частное решение тоже разыскивается по обычному алгоритму – с той поправкой, что увеличивается длительность процесса и его техническая сложность. Сначала используем начальное условие ![]() :
:
![]()
Далее находим первую производную ![]() и применяем начальное условие
и применяем начальное условие ![]() :
:
![]()
И, наконец, «окучиваем» вторую производную ![]() начальным условием
начальным условием ![]() :
:
![]()
Таким образом, у нас нарисовалась система трёх линейных уравнений с тремя неизвестными:
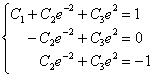
Здесь проще всего сложить почленно 2-е и 3-е уравнения, в результате чего получаем:
![]() – подставим по 2-е уравнение и выразим
– подставим по 2-е уравнение и выразим ![]() :
:
![]()
Надеюсь, все помнят действия со степенями, но всё же распишу их разок ОЧЕНЬ подробно:
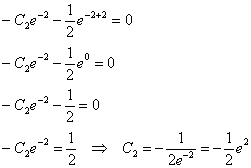
Почти всё готово. Подставим ![]() и
и ![]() в 1-е уравнение системы:
в 1-е уравнение системы:
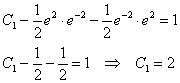
И на завершающем шаге подставим найденные значения констант в общее решение:
![]()
Ответ: частное решение: ![]()
С проверкой никаких чудес – сначала проверяем начальные условия:
![]() , ОК
, ОК
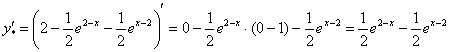
![]() , ОК
, ОК
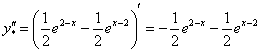
![]() , ОК
, ОК
После чего берём 3-ю производную 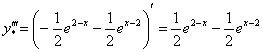 и подставляем её вместе с младшей сестрой
и подставляем её вместе с младшей сестрой ![]() в исходное дифференциальное уравнение
в исходное дифференциальное уравнение ![]() :
:
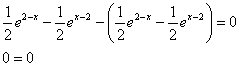
Получено верное равенство, таким образом, частное решение найдёно верно.
…Что-что не помешает, так это небольшая разминка:
Пример 2
Найти частное решение дифференциального уравнения ![]() , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям ![]()
Краткое решение и ответ в конце урока. Желающие разогреться поосновательнее могут «взять в оборот» ещё 30 примеров из задачника Рябушко (Часть 2, ИДЗ 11.4, Задача № 1), где для особых ценителей есть и диффуры 4-го порядка. Правильные ответы прилагаются!
Кстати, повторим немного алгебру – сколько слагаемых входит в общее решение ![]() однородного уравнения
однородного уравнения ![]() ?
?
Так как характеристический многочлен ![]() имеет ровно
имеет ровно ![]() комплексных корней, то таких слагаемых ровно «эн» штук:
комплексных корней, то таких слагаемых ровно «эн» штук: ![]() . А в случае неоднородности уравнения, понятно, больше – переходим к самому интересному:
. А в случае неоднородности уравнения, понятно, больше – переходим к самому интересному:
Линейные неоднородные уравнения высших порядков
![]()
Я буду придерживаться тех же обозначений, что и на уроке о неоднородных ДУ 2-го порядка. Для диффуров порядка ![]() общее решение имеет ту же самую структуру:
общее решение имеет ту же самую структуру:
![]() , где:
, где:
![]() – общее решение соответствующего однородного уравнения (в предыдущем параграфе обозначалось через
– общее решение соответствующего однородного уравнения (в предыдущем параграфе обозначалось через ![]() );
);
![]() – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
Как вы помните, наиболее трудной частью задачи является отыскание ![]() , для чего мы использовали таблицу подбора частного решения. Данная справка полезна и удобна, однако составлена она только для случая
, для чего мы использовали таблицу подбора частного решения. Данная справка полезна и удобна, однако составлена она только для случая ![]() . Как быть, если порядок уравнения выше? На самом деле можно вообще обойтись без таблицы! И сейчас я расскажу вам об одном удивительно простом приёме, который позволит избавиться от этого справочного балласта. Вернёмся к некоторым примерам статьи о неоднородных диффурах второго порядка:
. Как быть, если порядок уравнения выше? На самом деле можно вообще обойтись без таблицы! И сейчас я расскажу вам об одном удивительно простом приёме, который позволит избавиться от этого справочного балласта. Вернёмся к некоторым примерам статьи о неоднородных диффурах второго порядка:
В дифференциальном уравнении ![]() (Пример № 2) вроде бы нужно выполнить подбор в виде
(Пример № 2) вроде бы нужно выполнить подбор в виде ![]() , но если немного присмотреться к общему решению соответствующего однородного ДУ, то легко заметить, что константа там УЖЕ ЕСТЬ:
, но если немного присмотреться к общему решению соответствующего однородного ДУ, то легко заметить, что константа там УЖЕ ЕСТЬ: ![]() . Образно говоря, это место занято, и одинокая буква
. Образно говоря, это место занято, и одинокая буква ![]() в «очевидном» подборе – лишняя. Именно поэтому мы и повышаем степень домножением на «икс»:
в «очевидном» подборе – лишняя. Именно поэтому мы и повышаем степень домножением на «икс»: ![]()
Что характерно, итоговый ответ можно переписать «стильно»:
![]()
Прямо таки математическое событие под названием «Воссоединение членов многочлена» =)
В Примере же 1 для уравнения ![]() проходит «штатный» подбор
проходит «штатный» подбор ![]() – по той причине, что в общем решении
– по той причине, что в общем решении ![]() нет ничего подобного – ни куба, ни квадрата, ни линейного члена, ни константы.
нет ничего подобного – ни куба, ни квадрата, ни линейного члена, ни константы.
В уравнении ![]() (Пример 3) напрашивающийся подбор
(Пример 3) напрашивающийся подбор ![]() не годится, поскольку подобный член уже есть:
не годится, поскольку подобный член уже есть: ![]() , а значит, судьба наша
, а значит, судьба наша ![]() . И опять же – итоговый ответ можно красиво «упаковать»:
. И опять же – итоговый ответ можно красиво «упаковать»: ![]()
Для уравнения ![]() (Пример 6) ситуация интереснее: в нём не срабатывает подбор
(Пример 6) ситуация интереснее: в нём не срабатывает подбор ![]() и не помогает домножение на «икс»
и не помогает домножение на «икс» ![]() – оба «кандидата» уже присутствуют в общем решении:
– оба «кандидата» уже присутствуют в общем решении: ![]() . И поэтому ничего не остаётся, как ещё раз приподнять степень:
. И поэтому ничего не остаётся, как ещё раз приподнять степень: ![]() .
.
Думаю, теперь вам стал понятен неформальный смысл «аномальных» табличных случаев с домножением. И этот принцип так же работает для диффуров высших порядков! Впрочем, не будем торопиться:
Пример 3
Решить дифференциальное уравнение
![]()
Первый пункт решения пролетает на автопилоте:
![]()
![]() – сопряжённые комплексные корни, поэтому общее решение однородного ДУ:
– сопряжённые комплексные корни, поэтому общее решение однородного ДУ:
![]()
Но вот дальше хлопот побольше. Прежде всего, обращаем внимание, что правая часть неоднородного ДУ «разношёрстная» – в ней находятся синус с экспонентой. И возникает вопрос: как отыскать частное решение? Не спеша! В подобных ситуациях его удобно разделить на две части ![]() и «провернуть» алгоритм подбора два раза:
и «провернуть» алгоритм подбора два раза:
Примечание: эта возможность хоть и очевидна, однако строго доказывается в теории.
1) Первый кусок частного решения вроде бы надо искать в виде ![]() . Но подобные члены уже есть в общем решении
. Но подобные члены уже есть в общем решении ![]() , и поэтому «первоначальная версия» подлежит корректировке домножением на «икс»:
, и поэтому «первоначальная версия» подлежит корректировке домножением на «икс»:
![]()
Дальнейшее – дело техники, главное, тут не запутаться:
![]()
Вторую производную для надёжности лучше взять «столбиком»:
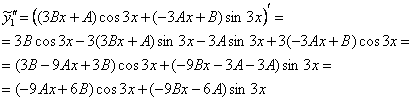
Этот приём я рекомендую использовать везде, где есть громоздкие выкладки, в частности при вычислении сложных кратных интегралов, коэффициентов ряда Фурье.
Подставим ![]() и
и ![]() в левую часть неоднородного уравнения, выполним упрощения и приравняем результат к
в левую часть неоднородного уравнения, выполним упрощения и приравняем результат к ![]() :
:
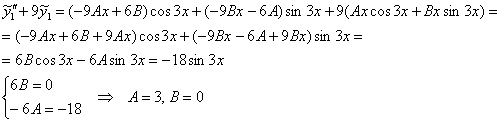
Таким образом: ![]()
Следует отметить, что в подобных технически сложных случаях выгоден более простой способ нахождения частного решения, связанный с применением аппарата комплексного анализа, однако в рамках данной статьи я оставлю его за кадром. Соответствующие примеры с пояснениями можно найти, например, в следующем решебнике:
Краснов М.Л., Киселёв А.И., Макаренко Г.И. Обыкновенные дифференциальные уравнения
2) Теперь разбираемся с экспонентой. Здесь проходит подбор в «штатном» виде ![]() , поскольку в общем решении
, поскольку в общем решении ![]() экспонент нет даже в помине.
экспонент нет даже в помине.
Тут всё гораздо проще:
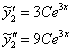
Подставим ![]() и
и ![]() в левую часть неоднородного ДУ, приведём подобные слагаемые и приравняем к
в левую часть неоднородного ДУ, приведём подобные слагаемые и приравняем к ![]() :
:
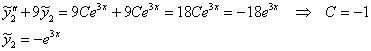
«Сведём» частное решение воедино:
![]()
Разумеется, его можно было найти и «за один присест», работая с ![]() , но к быстрому способу прикладывается жирный шанс что-нибудь где-нибудь потерять.
, но к быстрому способу прикладывается жирный шанс что-нибудь где-нибудь потерять.
Итак, общее решение неоднородного уравнения:
![]()
Скомпонуем «родственные» слагаемые:
Ответ: ![]()
Выполним проверку-«лайт». Во-первых, параноидально перепроверим, что числа ![]() являются корнями характеристического уравнения
являются корнями характеристического уравнения ![]() , а значит, слагаемые
, а значит, слагаемые ![]() находятся в ответе совершенно заслуженно; и, во-вторых, проверим частное решение
находятся в ответе совершенно заслуженно; и, во-вторых, проверим частное решение ![]() :
:
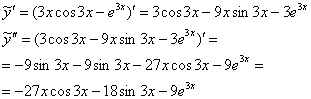
Подставим ![]() и
и ![]() в левую часть
в левую часть
неоднородного уравнения:
![]()
![]() – в результате получена правая часть, следовательно, частное решение найдено верно.
– в результате получена правая часть, следовательно, частное решение найдено верно.
Повышаем обороты:
Пример 4
Решить дифференциальное уравнение
![]()
Примерный образец чистового оформления задачи в конце урока. Ещё раз занудно остановлюсь на том, что частное решение желательно разбить на две части: ![]() – этот технический приём целесообразно применять во многих похожих случаях, за исключением совсем уж простых. Так, например, для правой части
– этот технический приём целесообразно применять во многих похожих случаях, за исключением совсем уж простых. Так, например, для правой части ![]() и подбора
и подбора ![]() разделять решение будет скорее, наоборот – лишней тратой времени. Хотя «разбивку» здесь тоже нельзя называть неуместной.
разделять решение будет скорее, наоборот – лишней тратой времени. Хотя «разбивку» здесь тоже нельзя называть неуместной.
Вторая часть урока будет посвящена наиболее распространённым на практике уравнениям, у которых в правой части находятся экспоненты и/или многочлены:
Пример 5
Найти общее решение дифференциального уравнения третьего порядка
![]()
…Мда…, бывает не только любовь, но и трудность с первого взгляда =)
Решение: найдём общее решение соответствующего однородного уравнения:
![]()
Первое, что приходит в голову, это подобрать какой-нибудь корень – здесь он обнаруживается быстро: ![]() , и разделить многочлен
, и разделить многочлен ![]() на
на ![]() . Или же воспользоваться схемой Горнера. Однако и в том, и в другом случае к нашей досаде выяснится, что
. Или же воспользоваться схемой Горнера. Однако и в том, и в другом случае к нашей досаде выяснится, что ![]() .
.
Всего-то лишь школьная формула куба суммы:
![]()
Но многие и многие студенты проходят мимо таких возможностей. Какой здесь можно дать совет? Решайте примеров больше и…париться будете меньше!
Итак, характеристическое уравнение имеет три кратных корня ![]() , поэтому:
, поэтому:
![]()
С частным решением на самом деле тоже всё просто. Смотрим на правую часть неоднородного уравнения, из которой напрашивается подбор ![]() , смотрим на «группу товарищей» из общего решения, и приходим к выводу, что ехать придётся на третьей полке:
, смотрим на «группу товарищей» из общего решения, и приходим к выводу, что ехать придётся на третьей полке: ![]() , ибо в общем решении
, ибо в общем решении ![]() и в подбираемом частном решении
и в подбираемом частном решении ![]() не должно быть подобных членов. Наконец-то сформулировал общее правило =) Если при «очевидном» подборе нарисовались подобные члены, то это лечится его домножением на «икс» (если нужно, 2 или бОльшее количество раз). Если не соблюсти это правило, то… проверьте сами.
не должно быть подобных членов. Наконец-то сформулировал общее правило =) Если при «очевидном» подборе нарисовались подобные члены, то это лечится его домножением на «икс» (если нужно, 2 или бОльшее количество раз). Если не соблюсти это правило, то… проверьте сами.
Производные – почти подарок:
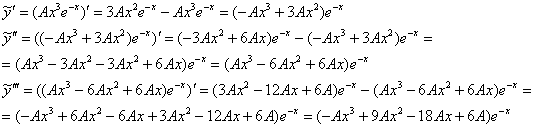
Подставим завоёванные трофеи в левую часть неоднородного уравнения, проведём упрощения и приравняем результат к правой части:
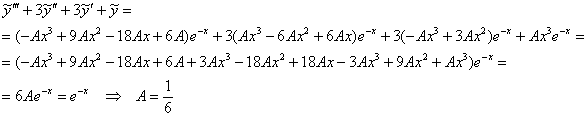
Если задание оформляется от руки, то подобные слагаемые удобно помечать и вычёркивать. И если после сокращений остаётся что-то «лишнее» – нужно искать ошибку: либо неправильно выбрана сама форма подбора, либо допущен огрех в производных, либо – в подстановке и финальных преобразованиях.
Таким образом: ![]()
Общее решение неоднородного уравнения:
![]()
Что называется, вся честнАя компания в одном купе:
Ответ: 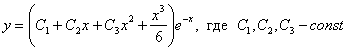
Не забываем о проверке! Хотя она здесь особо не нужна – маловероятно, что мы где-то ошиблись и всё так удачно «сошлось». Впрочем, для очистки совести можно «прозвонить» частное решение ![]() .
.
Очередной типовой пример для самостоятельного решения:
Пример 6
Найти общее решение дифференциального уравнения 3-го порядка
![]()
Краткое решение и ответ в конце урока, который мы завершаем приятнейшими задачами. Скоро поймёте, почему:)
Пример 7
Решить дифференциальное уравнение четвёртого порядка
![]()
Решение: с характеристическим уравнением никаких проблем:
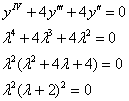
![]() – две пары кратных корней, таким образом:
– две пары кратных корней, таким образом:
![]()
А вот с частным решением всё несколько занятнее. Исходя из содержания правой части неоднородного ДУ, выдвигаем «штатную» версию подбора: ![]() , которая, понятно, нас не устраивает, поскольку в общем решении однородного ДУ уже есть
, которая, понятно, нас не устраивает, поскольку в общем решении однородного ДУ уже есть ![]() и
и ![]() . Домножением на «икс» вопрос не решить, так как подбор
. Домножением на «икс» вопрос не решить, так как подбор ![]() всё равно «пересекается» со слагаемым
всё равно «пересекается» со слагаемым ![]() общего решения . А значит, степень нужно поднять ещё выше:
общего решения . А значит, степень нужно поднять ещё выше:
![]()
Иметь дело с такими производными – действительно одно удовольствие:)
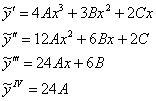
Подставим ![]() и
и ![]() в левую часть неоднородного уравнения, перегруппируем
в левую часть неоднородного уравнения, перегруппируем
слагаемые и приравняем результат к правой части:
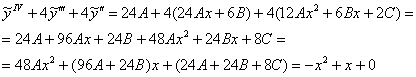
В результате получаем следующую систему линейных уравнений:
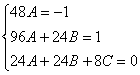
Дробей тушеваться не нужно – обычное дело, да и вычисления здесь устные. Из 1-го уравнения:
![]() – подставим во 2-е уравнение:
– подставим во 2-е уравнение:
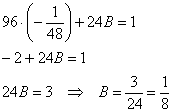
Подставим ![]() в 3-е уравнение:
в 3-е уравнение:
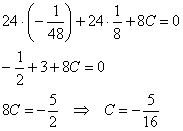
В результате: ![]()
Общее решение неоднородного уравнения:
![]()
И снова немного эстетики:
Ответ: ![]()
А почему бы и нет? – диффур пятого порядка для самостоятельного решения:
Пример 8
![]()
И коль скоро вы читаете эти строки, то, наверное, ждёте чего-нибудь особенного…. И я, конечно же, не могу обмануть этих ожиданий – пожалуйста, изящное и воздушное уравнение для полной релаксации:
Пример 9
Найти частное решение дифференциального уравнения ![]() , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям ![]()
Решения и ответы совсем близко.
Дополнительные тематические примеры с решениями можно посмотреть здесь (Задачи 12-15), а также в уже упомянутой книге Краснов М. Л., Киселёв А. И., Макаренко Г. И. Обыкновенные дифференциальные уравнения. Там же можно ознакомиться с линейными уравнениями с НЕпостоянными коэффициентами – когда среди ![]() есть коэффициенты с «иксами». Но разрешимы такие ДУ, понятно, далеко не всегда.
есть коэффициенты с «иксами». Но разрешимы такие ДУ, понятно, далеко не всегда.
...Признайтесь честно, вам понравилось?
Рекомендуйте друзьям!
Не понравилось?! …Ну что же, всяко бывает... – рекомендуйте недругам! =)
Решения и ответы:
Пример 2. Решение: составим и решим характеристическое уравнение:
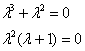
![]() – три действительных корня, среди которых есть два кратных, общее решение:
– три действительных корня, среди которых есть два кратных, общее решение: ![]() .
.
Найдём частное решение, соответствующее заданным начальным условиям:
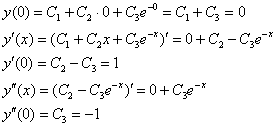
Составим и решим систему:
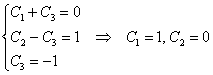
Ответ: ![]()
Пример 4. Решение: найдём общее решение соответствующего однородного уравнения:
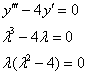
![]() – различные действительные корни, поэтому:
– различные действительные корни, поэтому:
![]()
Частное решение неоднородного уравнения найдём как сумму ![]()
1) Первую часть ищем в виде ![]()
Примечание: подбор ![]() не проходит, т. к. в общем решении уже есть подобный член:
не проходит, т. к. в общем решении уже есть подобный член: ![]() .
.
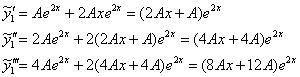
Подставим ![]() и
и ![]() в левую часть:
в левую часть:
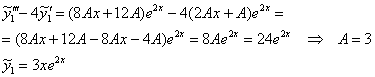
2) Вторую часть ищем в виде ![]()
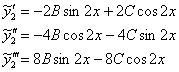
Подставим ![]() и
и ![]() в левую часть:
в левую часть:
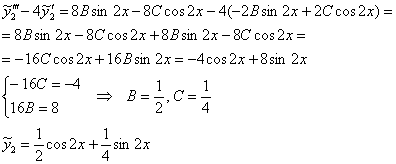
Таким образом:
![]()
Общее решение неоднородного уравнения:
![]()
Ответ: ![]()
Пример 6. Решение: найдём общее решение соответствующего однородного уравнения:
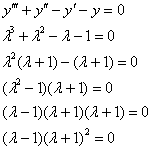
![]() , поэтому:
, поэтому: ![]()
Частное решение ищем в виде ![]()
Примечание: «очевидная» версия подбора ![]() не годится, поскольку в общем решении уже присутствует подобный член
не годится, поскольку в общем решении уже присутствует подобный член ![]() .
.
Найдём производные:
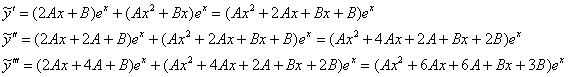
Подставим ![]() и
и ![]() в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:
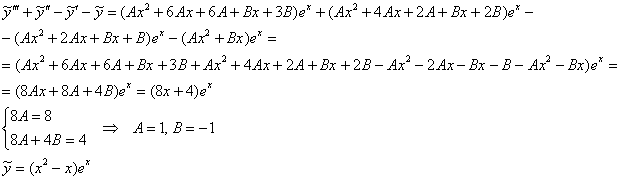
В результате:
![]()
Ответ: ![]()
Пример 8. Решение: найдём общее решение соответствующего однородного уравнения:
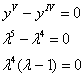
![]() , следовательно:
, следовательно:
![]()
Частное решение неоднородного ДУ ищем в виде: ![]()
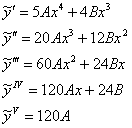
Подставим ![]() и
и ![]() в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:
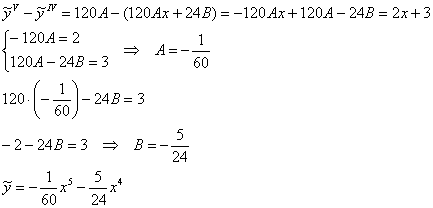
Таким образом:
![]()
Ответ: ![]()
Пример 9. Решение: найдём общее решение соответствующего однородного уравнения:
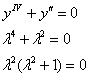
![]() , поэтому:
, поэтому:
![]()
Частное решение неоднородного уравнения ищем в виде: ![]()
![]()
Подставим ![]() и
и ![]() в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:
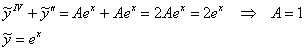
Общее решение неоднородного уравнения:
![]()
Найдём частное решение, соответствующее заданным начальным условиям:
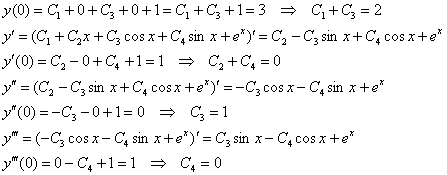
Составим и решим систему:
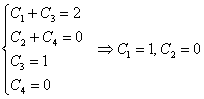
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
