
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Производная функции комплексной переменной.
Условия Коши-Римана. Краткая теория и примеры решений
Эпиграфы закончились,
Но будет послесловие…
Продолжаем наш курс ТФКП, и после изучения комплексных пределов на очереди производные. Сначала немного теории, затем много примеров, и на посошок смысл комплексной производной. …Если вы далеки от теории и тем паче от смысла, не тушуйтесь – появится и смысл и просветление, а уж практика будет разобрана под микроскопом, и решать вы наУчитесь :)
Формально производная функции комплексной переменной определяется почти так же, как в действительном случае. Рассмотрим однозначную функцию ![]() , которая определена в некоторой области
, которая определена в некоторой области ![]() . Возьмём точку
. Возьмём точку ![]() и зададим в ней приращение
и зададим в ней приращение ![]() – так, чтобы точка
– так, чтобы точка ![]() тоже принадлежала области
тоже принадлежала области ![]() . При этом «добавку» «дельта зет» мы можем «отмерять» произвольно в любую сторону от точки «зет». Заданному приращению аргумента
. При этом «добавку» «дельта зет» мы можем «отмерять» произвольно в любую сторону от точки «зет». Заданному приращению аргумента ![]() , очевидно, соответствует приращение функции
, очевидно, соответствует приращение функции ![]() , и определение:
, и определение:
если существует конечный предел ![]() при
при ![]() произвольным образом, то он называется производной функции
произвольным образом, то он называется производной функции ![]() в точке
в точке ![]() :
:
![]()
Варианты обозначений: ![]() («дэ эф по дэ зет»),
(«дэ эф по дэ зет»), ![]() – кому как нравится, кому как требуется.
– кому как нравится, кому как требуется.
Функцию ![]() , имеющую производную в точке
, имеющую производную в точке ![]() , называют дифференцируемой в этой точке. Но это ещё не всё. Поскольку предел
, называют дифференцируемой в этой точке. Но это ещё не всё. Поскольку предел ![]() должен существовать при любом стремлении
должен существовать при любом стремлении ![]() , то на функцию накладываются дополнительные условия, получившие фамилию Коши и Римана. Условий два и состоят они в следующих равенствах частных производных:
, то на функцию накладываются дополнительные условия, получившие фамилию Коши и Римана. Условий два и состоят они в следующих равенствах частных производных:
![]() ,
,
где ![]() и
и ![]() – действительная и мнимая часть функции
– действительная и мнимая часть функции ![]() . Буковки «у» и «вэ», напоминаю – есть функции двух действительных переменных.
. Буковки «у» и «вэ», напоминаю – есть функции двух действительных переменных.
Техническое замечание: частные производные в рассматриваемой теме, как правило, обозначают ![]() , старайтесь не использовать запись
, старайтесь не использовать запись ![]() .
.
Итак, чтобы производная существовала необходимо выполнение условий Коши-Римана, и в то же самое время (с определённой оговоркой) этого достаточно. Если условия Коши-Римана не выполнены в той или иной точке, то производной не существует в этой точке. Желающие могут найти обоснование этих фактов, например, в рекомендованных книгах.
Помимо дифференцируемости, в комплексном анализе есть ещё одно очень важное понятие:
если функция дифференцируема не только в точке ![]() , но и некоторой её окрестности (пусть очень малой), то её (функцию) называют аналитической в этой точке.
, но и некоторой её окрестности (пусть очень малой), то её (функцию) называют аналитической в этой точке.
Если функция дифференцируема во всех точках некоторой области ![]() , то она, очевидно, аналитична в этой области. Такую функцию называют аналитической или регулярной в области
, то она, очевидно, аналитична в этой области. Такую функцию называют аналитической или регулярной в области ![]() . Или голоморфной. Область «дэ», в частности, может представлять собой всю комплексную плоскость
. Или голоморфной. Область «дэ», в частности, может представлять собой всю комплексную плоскость ![]() .
.
Все элементарные функции аналитичны в своей области определения. Многие из них мы рассмотрели на первом уроке, ну а наиболее популярные на практике я перечислил в конце этой статьи. И мы, собственно, переходим к практическим задачам:
Пример 1
Выяснить, будет ли функция дифференцируема и аналитична хоть в какой-то точке комплексной плоскости:
а) ![]() ,
,
б) ![]() ,
,
в) ![]()
Чтобы исследовать функцию на дифференцируемость, нужно найти её действительную и мнимую часть и проверить условия Коши-Римана. Если они выполнены не только в точке (той или иной), а ещё и в её окрестности (хотя бы какой-то), то функция не только дифференцируема, но и аналитична в этой точке.
Решение: а) Вспоминаем, что «зет» с чёрточкой – это сопряжённое ![]() по отношению к
по отношению к ![]() число. Таким образом, функция
число. Таким образом, функция ![]() возвращает сопряжённые к аргументу значения. Видно, как ясный день, что:
возвращает сопряжённые к аргументу значения. Видно, как ясный день, что:
![]() – действительная часть этой функции, а
– действительная часть этой функции, а ![]() – её мнимая часть.
– её мнимая часть.
Найдём частные произвольные первого порядка сих частей:
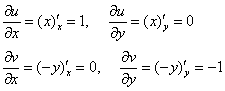
– и тут я кратко напомню основное правило: когда мы дифференцируем по «икс», то переменная «игрек» считается константой. И, наоборот – при дифференцировании по «игрек», константой считается «икс».
Проверим выполнение условий Коши-Римана, впрочем, чего тут проверять – светит солнце. Первое условие ![]() не выполнено
не выполнено ![]() , а второе
, а второе ![]() – да:
– да: ![]() , хотя, это уже не важно.
, хотя, это уже не важно.
Вывод: условия Коши-Римана не выполнены ни в одной точке комплексной плоскости ![]() , поэтому функция нигде не дифференцируема и тем более не аналитична.
, поэтому функция нигде не дифференцируема и тем более не аналитична.
Вот оно как может быть, а ведь функция ![]() определена и даже непрерывна на
определена и даже непрерывна на ![]() . Но этого ещё не достаточно для существования производной.
. Но этого ещё не достаточно для существования производной.
б) Рассмотрим функцию ![]() . Множитель
. Множитель ![]() возвращает действительную часть аргумента
возвращает действительную часть аргумента ![]() , поэтому
, поэтому ![]() . Таким образом:
. Таким образом:
![]() – действительная часть функции, а
– действительная часть функции, а ![]() – её мнимая часть.
– её мнимая часть.
Найдём частные производные первого порядка:
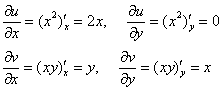
Проверим условия Коши-Римана:
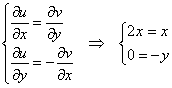
Очевидно, условия выполнены только при ![]() , то есть в единственной точке
, то есть в единственной точке ![]() комплексной плоскости.
комплексной плоскости.
Вывод: функция ![]() дифференцируема лишь в точке
дифференцируема лишь в точке ![]() , но не аналитична в ней (т. к. не дифференцируема в любой окрестности этой точки).
, но не аналитична в ней (т. к. не дифференцируема в любой окрестности этой точки).
в) И для функции ![]() я разберу всё крайне подробно, поскольку такие вещи предлагают людям, зачастую далёким от математики.
я разберу всё крайне подробно, поскольку такие вещи предлагают людям, зачастую далёким от математики.
Сначала решение, затем комментарии. Независимая переменная «зет», как вы помните, записывается в виде ![]() , поэтому:
, поэтому:
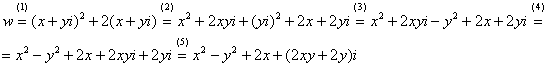
(1) В исходную функцию ![]() подставили
подставили ![]() .
.
(2) Для первого слагаемого использовали формулу сокращенного умножения ![]() . В слагаемом
. В слагаемом ![]() – раскрыли скобки.
– раскрыли скобки.
(3) Аккуратно возвели в квадрат ![]() , не забывая, что
, не забывая, что ![]()
(4) Перегруппировка слагаемых: сначала переписываем слагаемые, в которых нет мнимой единицы (первая группа), затем слагаемые, где есть ![]() (вторая группа). Следует отметить, что перетасовывать слагаемые не обязательно, и данный этап можно пропустить (фактически выполнив его устно).
(вторая группа). Следует отметить, что перетасовывать слагаемые не обязательно, и данный этап можно пропустить (фактически выполнив его устно).
(5) У второй группы выносим ![]() за скобки.
за скобки.
В результате наша функция оказалась представлена в виде ![]() , где:
, где:
![]() – действительная часть функции.
– действительная часть функции.
![]() – её мнимая часть.
– её мнимая часть.
Найдём частные производные первого порядка:
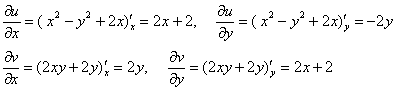
– производные тут устные, но если у вас всё ещё сложности с ними – наверстайте материал по ссылке выше.
Проверим выполнение условий Коши-Римана:
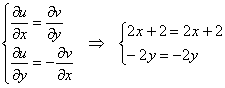
В результате получены тождества (равенства, верные для всех значений ![]() ), поэтому функция
), поэтому функция ![]() дифференцируема во всех точках комплексной плоскости, и, очевидно, регулярна в ней – по той причине, что в окрестности (причём, любой) любой точки – функция дифференцируема.
дифференцируема во всех точках комплексной плоскости, и, очевидно, регулярна в ней – по той причине, что в окрестности (причём, любой) любой точки – функция дифференцируема.
Вывод: функция дифференцируема и аналитична на всей комплексной плоскости.
Аналогичное задание для самостоятельного решения:
Пример 2
Исследовать функции на дифференцируемость и аналитичность:
а) ![]() ,
,
б) ![]() ,
,
в) ![]() и тут из практических соображений я сразу запишу действительную
и тут из практических соображений я сразу запишу действительную ![]() и мнимую часть
и мнимую часть ![]() этой функции, которые мы нашли ещё в Примере 6 вводного урока. Потому что сейчас наша задача – поразмять частные производные.
этой функции, которые мы нашли ещё в Примере 6 вводного урока. Потому что сейчас наша задача – поразмять частные производные.
Решаем, сверяемся и продолжаем.
Как найти производную комплексной функции?
Во-первых, производную можно найти по определению – аналогично действительному случаю. Но это вам грозит, скорее всего, только в том случае, если вы учитесь профильно и / или углублённо.
И во-вторых, у меня отличная новость! Для функции комплексной переменной ![]() работают те же правила дифференцирования и таблица производных, в том числе всё это справедливо (с некоторыми оговорками) и для многозначных функций, а-ка корни, логарифмы, «арки». Только вместо буковки «икс» нужно использовать букву «зет».
работают те же правила дифференцирования и таблица производных, в том числе всё это справедливо (с некоторыми оговорками) и для многозначных функций, а-ка корни, логарифмы, «арки». Только вместо буковки «икс» нужно использовать букву «зет».
И, конечно, для той или иной функции, которую мы дифференцируем, должны быть выполнены условия Коши-Римана. Только в этом случае будет существовать производная!
Так, в Примере 1, пункте «в» условия Коши-Римана выполнены, и мы можем с лёгким сердцем найти производную по обычной схеме:
![]()
В Примере 2, пунктах «б», «в» аналогично:
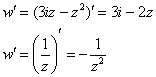
Напоминаю (и это прекрасно видно), что производная ![]() – это тоже функция, смысл которой мы проясним после наработки практики.
– это тоже функция, смысл которой мы проясним после наработки практики.
Но перед тем как решать, обратим внимание на пару полезных формул. В первом же примере было выяснено, что ![]() .
.
Теперь куб. Используя формулу сокращенного умножения ![]() , выведем:
, выведем:
![]() .
.
Рекомендую переписать в тетрадь две рабочие формулы:
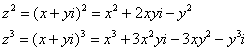
Формулы очень удобно использовать на практике, поскольку они значительно ускоряют процесс решения.
Пример 3
Определить действительную ![]() и мнимую
и мнимую ![]() части функции
части функции ![]() . Проверить условия Коши-Римана. В случае их выполнения, найти производную функции.
. Проверить условия Коши-Римана. В случае их выполнения, найти производную функции.
Решение раскладывается на три последовательных этапа:
1) Найдём действительную и мнимую часть функции. Это задание было неоднократно разобрано в предыдущих примерах, поэтому запишу без комментариев.
Так как ![]() , то:
, то:
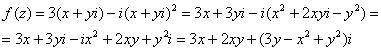
Таким образом:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Остановлюсь еще на одном техническом моменте: в каком порядке записывать слагаемые в действительной и мнимой частях? Да, в принципе, без разницы. Например, действительную часть можно записать так: ![]() , а мнимую – так:
, а мнимую – так: ![]() .
.
3) Проверим выполнение условий Коши Римана. Обычно это удобнее делать последовательно – сначала одно, затем другое.
Начнем с проверки условия ![]() . Находим частные производные:
. Находим частные производные:
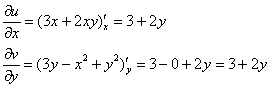
Таким образом, условие ![]() выполнено.
выполнено.
Несомненно, приятная новость – частные производные почти всегда очень простые.
Проверяем выполнение второго условия ![]() :
:
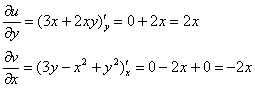
Получилось одно и то же, но с разными знаками, то есть условие ![]() также выполнено.
также выполнено.
Условия Коши-Римана выполнены на всей комплексной плоскости, как оно чаще всего бывает в «массовой практике». Следовательно, функция дифференцируема (по умолчанию – всюду).
3) Найдём производную функции. Производная тоже очень простая и находится по обычным правилам:
![]()
Мнимая единица – это константа, и при дифференцировании обращаемся с ней соответствующим образом.
Ответ: ![]() – действительная часть,
– действительная часть, ![]() – мнимая часть.
– мнимая часть.
Условия Коши-Римана выполнены, ![]() .
.
Кроме того, существуют иной способ нахождения производной – не пропускаем! Эта информация крайне полезна для понимания следующего урока – Как найти функцию комплексной переменной?
Суть состоит в том, что производную можно сконструировать из частных производных по формуле:
![]()
В нашем примере: ![]() , таким образом:
, таким образом:
![]()
Теперь предстоит решить обратную задачу – в полученном выражении нужно вычленить ![]() . Для того, чтобы это сделать, нужно в слагаемых
. Для того, чтобы это сделать, нужно в слагаемых ![]() и
и ![]() вынести
вынести ![]() за скобку:
за скобку:
![]()
Обратное действие, как многие заметили, выполнять несколько труднее, поэтому тут лучше выполнить промежуточную проверку – берём выражение ![]() , устно либо на черновике раскрываем скобки и убеждаемся, что получилось именно
, устно либо на черновике раскрываем скобки и убеждаемся, что получилось именно ![]() .
.
Имея в виду условия Коши-Римана ![]() , формулу можно записать следующим образом:
, формулу можно записать следующим образом:
![]()
В данном случае: ![]() , поэтому:
, поэтому:
![]()
И, используя те же условия, производную можно выразить ещё двумя способами:
![]()
Откуда выявляется важный факт: аналитическая (!) функция ![]() однозначно определяется своей действительной либо мнимой частью. Если мы знаем одну из этих частей, то, по сути, знаем и функцию. Чтобы найти производную, достаточно взять частные производные от известной части и использовать одну из формул, которые я только что привёл выше.
однозначно определяется своей действительной либо мнимой частью. Если мы знаем одну из этих частей, то, по сути, знаем и функцию. Чтобы найти производную, достаточно взять частные производные от известной части и использовать одну из формул, которые я только что привёл выше.
Однако возвращаемся в основное русло, аналогичный пример для самостоятельного решения:
Пример 4
Определить действительную ![]() и мнимую
и мнимую ![]() части функции
части функции ![]() . Проверить выполнение условий Коши-Римана и найти производную.
. Проверить выполнение условий Коши-Римана и найти производную.
Но перед тем как с шашками наголо броситься в бой на комплексной плоскости, я напомню главное правило при работе с комплексными числами:
БУДЬТЕ ВНИМАТЕЛЬНЫ! Внимательным нужно быть, конечно, везде, но в комплексных числах следует быть внимательным, как никогда! Помните, что ![]() , аккуратно раскрывайте скобки, ничего не теряйте. По моим наблюдениям, самой распространенной ошибкой является потеря знака. Не спешите!
, аккуратно раскрывайте скобки, ничего не теряйте. По моим наблюдениям, самой распространенной ошибкой является потеря знака. Не спешите!
Краткое решение и примерный образец чистового оформления примера в конце урока.
Усложним наши функции:
Пример 5
Определить действительную ![]() и мнимую
и мнимую ![]() части функции
части функции ![]() . Проверить выполнение условий Коши-Римана. Вычислить
. Проверить выполнение условий Коши-Римана. Вычислить ![]()
Алгоритм решения полностью сохраняется, но в конце добавится новый пунктик: нахождение производной в точке. Для куба нужная формула уже выведена: ![]()
Определим действительную и мнимую части предложенной функции.
Внимание и еще раз внимание!
Так как ![]() , то:
, то:
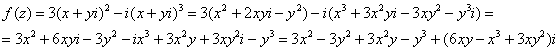
Таким образом:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – её мнимая часть.
– её мнимая часть.
Проверим выполнение условий Коши-Римана:
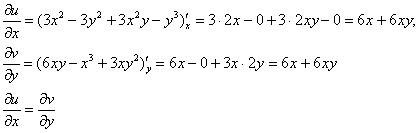
Проверка второго условия:
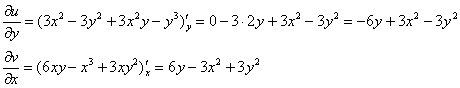
Получилось одно и то же, но с разными знаками, то есть условие ![]() также выполнено.
также выполнено.
Условия Коши-Римана выполнены (по умолчанию – всюду), следовательно, функция является дифференцируемой:
![]()
Вычислим значение производной в требуемой точке:
![]()
Ответ: ![]() ,
, ![]() , условия Коши-Римана выполнены,
, условия Коши-Римана выполнены, ![]()
Функции с кубами встречаются очень часто, поэтому пример для закрепления:
Пример 6
Определить действительную ![]() и мнимую
и мнимую ![]() части функции
части функции ![]() . Проверить выполнение условий Коши-Римана. Вычислить
. Проверить выполнение условий Коши-Римана. Вычислить ![]() .
.
Образец для сверки в конце урока.
Теперь переходим к другим элементарным функциям. Начнём с комплексной экспоненты. Для решения тематической задачи нам потребуется формула Эйлера:
![]() – для любого действительного числа
– для любого действительного числа ![]() ,
,
и я сразу запишу версию для «минус альфа»:
![]()
И вы тоже запишИте их к себе в тетрадь, чтобы они были перед глазами.
Пример 7
Определить действительную ![]() и мнимую
и мнимую ![]() части функции
части функции ![]() . Проверить выполнение условий Коши-Римана. Найти производную.
. Проверить выполнение условий Коши-Римана. Найти производную.
Решение: генеральная линия партии остаётся непоколебимой – сначала выделяем действительную и мнимую части функции. Приведу подробное решение, и ниже закомментирую каждый шаг.
Поскольку ![]() , то:
, то:
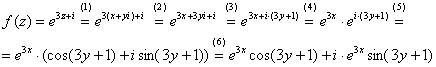
(1) Подставляем ![]() вместо «зет».
вместо «зет».
(2) После подстановки нужно выделить действительную и мнимую часть сначала в показателе экспоненты. Для этого раскрываем скобки.
(3) Группируем мнимую часть показателя, вынося мнимую единицу за скобки.
(4) Используем школьное действие со степенями.
(5) Для множителя ![]() используем формулу Эйлера
используем формулу Эйлера ![]() , при этом
, при этом ![]() .
.
(6) Раскрываем скобки, в результате:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Дальнейшие действия стандартны, проверим выполнение условий Коши-Римана:
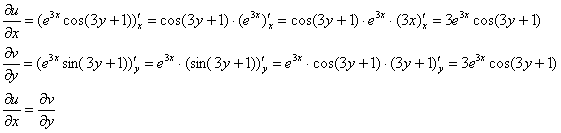
Частные производные опять не очень сложные, но на всякий пожарный расписал их максимально подробно. Проверяем второе условие:
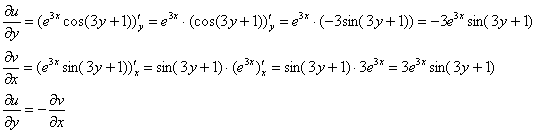
Условия Коши-Римана выполнены, найдём производную. По правилу дифференцирования сложной функции:
![]()
Ответ: ![]() ,
, ![]() , условия Коши-Римана выполнены,
, условия Коши-Римана выполнены, ![]()
Аналогичное задание для самостоятельного решения:
Пример 8
Определить действительную ![]() и мнимую
и мнимую ![]() части функции
части функции ![]() . Проверить выполнение условий Коши-Римана, найти производную.
. Проверить выполнение условий Коши-Римана, найти производную.
! Внимание! Знак «минус» справа ![]() относится к мнимой части:
относится к мнимой части: ![]() . Терять минус нельзя!
. Терять минус нельзя!
Полное решение и ответ в конце урока.
Та же задача с комплексным синусом либо косинусом решается с помощью формул:
![]()
– их я тоже освещал на первом же уроке.
Параметры «альфа» и «бета», принимают только действительные значения, в том числе они могут быть функциями действительных переменных.
Также обратите внимание, что в формулах есть гиперболические функции, при дифференцировании они превращаются друг в друга, не случайно я включил их в таблицу производных.
Пример 9
Определить действительную ![]() и мнимую
и мнимую ![]() части функции
части функции ![]() . Найти производную, если это возможно.
. Найти производную, если это возможно.
Решение: алгоритм решения очень похож на предыдущие два примера, но есть очень важные моменты, поэтому начальный этап я опять закомментирую пошагово.
Поскольку ![]() , то:
, то:
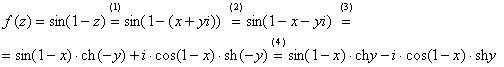
1) Подставляем ![]() вместо «зет».
вместо «зет».
(2) Сначала выделяем действительную и мнимую часть внутри синуса. В этих целях раскрываем скобки.
(3) Используем формулу ![]() , при этом
, при этом ![]() .
.
(4) Используем чётность гиперболического косинуса: ![]() и нечётность гиперболического синуса:
и нечётность гиперболического синуса: ![]() . Гиперболики хоть и не от мира студенческого, но во многом напоминают аналогичные тригонометрические функции.
. Гиперболики хоть и не от мира студенческого, но во многом напоминают аналогичные тригонометрические функции.
В итоге:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Внимание! Знак «минус» относится к мнимой части, и его ни в коем случае не теряем! Для наглядной иллюстрации полученный выше результат можно переписать так:
![]()
Проверим выполнение условий Коши-Римана:
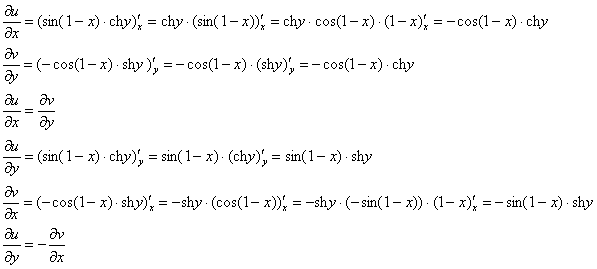
Условия Коши-Римана выполнены, значит, функция дифференцируема.
По правилу дифференцирования сложной функции:
![]()
Ответ: ![]() ,
, ![]() ,
, ![]()
С косинусом, дамы и господа, разбираемся самостоятельно:
Пример 10
Найти производную функции ![]() , если это возможно.
, если это возможно.
И в заключение ответим на важный практический вопрос:
что делать, если в таком задании условия Коши-Римана «не сошлись»?
– Возможно, так и было задумано, особенно если дана какая-нибудь «нестандартная» функция, как в первых примерах. И особенно, если математика у вас основательная.
– Вы допустили ошибку. Опечаток здесь быть не может. Дело в том, что элементарные функции аналитичны в своих областях определения, и условия Коши-Римана просто обязаны выполняться. Это, в частности:
– рациональная («многочленная») функция, типичные представители были в Примерах 3-6;
– дробно-рациональная функция (многочлены в числителе и знаменателе) – дифференцируема всюду, за исключением точек, где знаменатель обращается в ноль, простейшим представителем можно считать ![]() (Пример 2в);
(Пример 2в);
– комплексная экспонента;
– комплексный синус и косинус;
– комплексный гиперболический синус и косинус, к слову, как их решать? Просто пользуемся определениями ![]() ,
, ![]() – и разбираемся с двумя экспонентами по образцу Примеров 7-8.
– и разбираемся с двумя экспонентами по образцу Примеров 7-8.
а также:
– сумма / разность, произведение / частное и композиция элементарных функций. Это, кстати, сама дробно-рациональная функция (деление двух многочленов) и, например, сложная (композиционная) функция ![]() , опционально её можно ещё домножить, да хотя на «зет». Все они заведомо аналитичны в своих областях определения.
, опционально её можно ещё домножить, да хотя на «зет». Все они заведомо аналитичны в своих областях определения.
Главное, всё внимательно перепроверить и не впадать в ступор.
И в качестве эпилога как раз короткая история про ступор, или о том, какие вопросы преподавателей являются самыми сложными. Самые сложные вопросы, как ни странно – это вопросы с очевидными ответами. А история такова: сдаёт человек экзамен по алгебре, тема билета: «Следствие основной теоремы алгебры». Экзаменатор слушает-слушает, а потом вдруг спрашивает: «А откуда это следует?». Вот это был ступор, так ступор. Вся аудитория уже угорала, но студент так и не сказал правильного ответа: «из основной теоремы алгебры».
Вспоминаю историю и из личного опыта, сдаю физику, что-то там про давление жидкости, что уже не помню, но рисунок остался в памяти навсегда – изогнутая труба, по которой текла жидкость. Ответил я билет «на отлично», причем даже сам понял, что ответил. И вот преподаватель напоследок спрашивает: «Где здесь трубка тока?». Крутил-вертел я этот чертёж с изогнутой трубой минут пять, высказывал самые дикие версии, пилил трубу, рисовал какие-то проекции. А ответ был прост, трубка тока – это вся труба.
Неплохо разгрузились, до скорой встречи на уроке Как найти функцию комплексной переменной? – по известной действительной или мнимой части.
Всем желаю не тормозить, иногда очевидное – это самое сложное!
Решения и ответы:
Пример 2. Решение:
а) Запишем действительную и мнимую часть функции ![]() :
:
![]()
Найдём частные произвольные первого порядка:
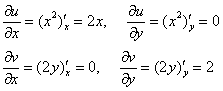
Проверим условия Коши-Римана:
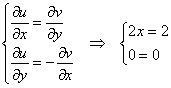
Таким образом, условия Коши-Римана выполнены лишь для чисел ![]() с действительной частью
с действительной частью ![]() . В любой окрестности любого из этих чисел есть точки, в которых функция не дифференцируема, поэтому функция не аналитична в них.
. В любой окрестности любого из этих чисел есть точки, в которых функция не дифференцируема, поэтому функция не аналитична в них.
Вывод: функция дифференцируема в точках с действительной частью ![]() и не регулярна в комплексной плоскости.
и не регулярна в комплексной плоскости.
б) Так как ![]() , то:
, то:
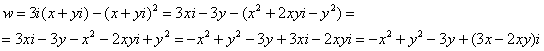
Таким образом, ![]() – действительная часть,
– действительная часть, ![]() – мнимая часть.
– мнимая часть.
Найдём частные производные:
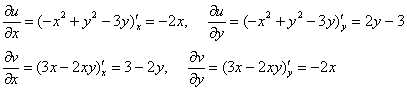
и проверим условия Коши-Римана:
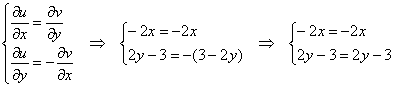
Условия Коши-Римана выполнены для всех значений ![]() .
.
Вывод: функция дифференцируема во всех точках комплексной плоскости, а значит, регулярна в ней.
в) Найдём частные производные и проверим условия Коши-Римана. Это можно сделать в такой редакции:
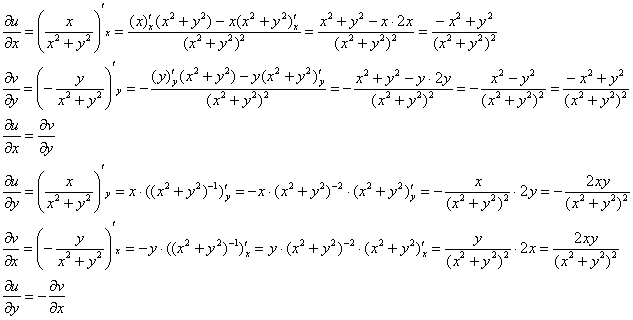
Условия Коши-Римана выполнены во всех точках комплексной плоскости, кроме ![]() , где функция
, где функция ![]() не определена.
не определена.
Вывод: функция регулярна на всей комплексной плоскости кроме точки ![]() .
.
Пример 4. Решение: так как ![]() , то:
, то:
![]()
Таким образом:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Проверим выполнение условий Коши Римана:
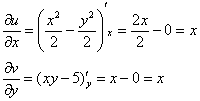
Условие ![]() выполнено.
выполнено.
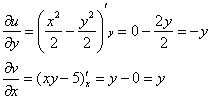
Условие ![]() также выполнено.
также выполнено.
Условия Коши-Римана выполнены, найдём производную:
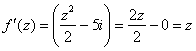
Ответ: ![]() – действительная часть,
– действительная часть, ![]() – мнимая часть.
– мнимая часть.
Условия Коши-Римана выполнены, ![]() .
.
Пример 6. Решение: определим действительную и мнимую части данной функции.
Так как ![]() , то:
, то:
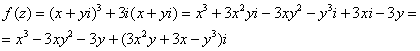
Таким образом:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Проверим выполнение условий Коши-Римана:
![]()
![]()
Условия Коши-Римана выполнены:
![]()
![]()
Ответ: ![]() ,
, ![]() , условия Коши-Римана выполнены,
, условия Коши-Римана выполнены, ![]()
Пример 8. Решение: так как ![]() , то:
, то:
![]()
Таким образом:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Проверим выполнение условий Коши-Римана:
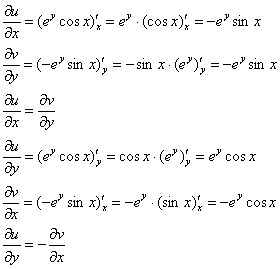
Условия Коши-Римана выполнены, найдём производную:
![]()
Ответ: ![]() ,
, ![]() , условия Коши-Римана выполнены,
, условия Коши-Римана выполнены, ![]()
Пример 10. Решение: найдём действительную и мнимую часть функции. Так как ![]() , то:
, то:
![]()
Таким образом:
![]() – действительная часть функции
– действительная часть функции ![]() ;
;
![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Проверим выполнение условий Коши-Римана:
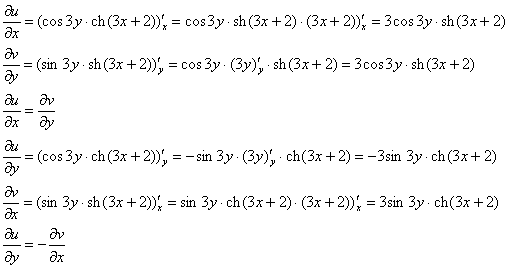
Условия Коши-Римана выполнены.
По правилу дифференцирования сложной функции:
![]()
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
