
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Уравнение плоскости. Как составить уравнение плоскости?
Взаимное расположение плоскостей. Задачи
Пространственная геометрия не намного сложнее «плоской» геометрии, и наши полёты в пространстве начинаются с данной статьи. Для усвоения темы необходимо хорошо разобраться в векторах, кроме того, желательно быть знакомым с геометрией плоскости – будет много похожего, много аналогий, поэтому информация переварится значительно лучше. В серии моих уроков 2D-мир открывается статьёй Уравнение прямой на плоскости. Но сейчас Бэтмен сошёл с плоского экрана телевизора и стартует с космодрома Байконур.
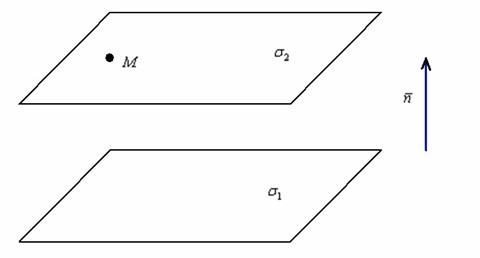
Начнём с чертежей и обозначений. Схематически плоскость можно нарисовать в виде параллелограмма, что создаёт впечатление пространства:

Плоскость бесконечна, но у нас есть возможность изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко. Мне по техническим причинам удобнее изображать плоскость именно так и именно в таком положении. Реальные плоскости, которые мы рассмотрим в практических примерах, могут располагаться как угодно – мысленно возьмите чертёж в руки и покрутите его в пространстве, придав плоскости любой наклон, любой угол.
Обозначения: плоскости принято обозначать маленькими греческими буквами ![]() , видимо, чтобы не путать их с прямой на плоскости или с прямой в пространстве. Я привык использовать букву
, видимо, чтобы не путать их с прямой на плоскости или с прямой в пространстве. Я привык использовать букву ![]() . На чертеже именно буква «сигма», а вовсе не дырочка. Хотя, дырявая плоскость, это, безусловно, весьма забавно.
. На чертеже именно буква «сигма», а вовсе не дырочка. Хотя, дырявая плоскость, это, безусловно, весьма забавно.
В ряде случаев для обозначения плоскостей удобно использовать те же греческие буквы с нижними подстрочными индексами, например, ![]() .
.
Очевидно, что плоскость однозначно определяется тремя различными точками, не лежащими на одной прямой. Поэтому достаточно популярны трёхбуквенные обозначения плоскостей – по принадлежащим им точкам, например, ![]() и т.д. Нередко буквы заключают в круглые скобки:
и т.д. Нередко буквы заключают в круглые скобки: ![]() , чтобы не перепутать плоскость с другой геометрической фигурой.
, чтобы не перепутать плоскость с другой геометрической фигурой.
Для опытных читателей приведу меню быстрого доступа:
- Общее уравнение плоскости
- Как составить уравнение плоскости по точке и двум векторам?
- Как составить уравнение плоскости по трём точкам?
- Нормальный вектор плоскости
- Как составить уравнение плоскости по точке и вектору нормали?
- Как построить плоскость, параллельную данной?
- Как найти расстояние от точки до плоскости?
- Взаимное расположение плоскостей:
и мы не будем томиться долгими ожиданиями:
Общее уравнение плоскости
Общее уравнение плоскости имеет вид ![]() , где коэффициенты
, где коэффициенты ![]() одновременно не равны нулю.
одновременно не равны нулю.
Ряд теоретических выкладок и практических задач справедливы как для привычного ортонормированного базиса, так и для аффинного базиса пространства (если масло - масляное, вернитесь к уроку Линейная (не) зависимость векторов. Базис векторов). Для простоты будем полагать, что все события происходят в ортонормированном базисе и декартовой прямоугольной системе координат.
А теперь немного потренируем пространственное воображение. Ничего страшного, если у вас оно плохое, сейчас немного разовьём. Даже для игры на нервах нужны тренировки.
В самом общем случае, когда числа ![]() не равны нулю, плоскость пересекает все три координатные оси. Например, так:
не равны нулю, плоскость пересекает все три координатные оси. Например, так:
Ещё раз повторю, что плоскость бесконечно продолжается во все стороны, и у нас есть возможность изобразить только её часть.
Рассмотрим простейшие уравнения плоскостей:
![]()
Как понимать данное уравнение? Вдумайтесь: «зет» ВСЕГДА, при любых значениях «икс» и «игрек» равно нулю. Это уравнение «родной» координатной плоскости ![]() . Действительно, формально уравнение можно переписать так:
. Действительно, формально уравнение можно переписать так: ![]() , откуда хорошо видно, что нам по барабану, какие значения принимают «икс» и «игрек», важно, что «зет» равно нулю.
, откуда хорошо видно, что нам по барабану, какие значения принимают «икс» и «игрек», важно, что «зет» равно нулю.
Аналогично:
![]() – уравнение координатной плоскости
– уравнение координатной плоскости ![]() ;
;
![]() – уравнение координатной плоскости
– уравнение координатной плоскости ![]() .
.
Немного усложним задачу, рассмотрим плоскость ![]() (здесь и далее в параграфе предполагаем, что числовые коэффициенты не равны нулю). Перепишем уравнение в виде:
(здесь и далее в параграфе предполагаем, что числовые коэффициенты не равны нулю). Перепишем уравнение в виде: ![]() . Как его понимать? «Икс» ВСЕГДА, при любых значениях «игрек» и «зет» равно некоторому числу
. Как его понимать? «Икс» ВСЕГДА, при любых значениях «игрек» и «зет» равно некоторому числу ![]() . Эта плоскость параллельна координатной плоскости
. Эта плоскость параллельна координатной плоскости ![]() . Например, плоскость
. Например, плоскость ![]() параллельна плоскости
параллельна плоскости ![]() и проходит через точку
и проходит через точку ![]() .
.
Аналогично:
![]() – уравнение плоскости, которая параллельна координатной плоскости
– уравнение плоскости, которая параллельна координатной плоскости ![]() ;
;
![]() – уравнение плоскости, которая параллельна координатной плоскости
– уравнение плоскости, которая параллельна координатной плоскости ![]() .
.
Добавим членов: ![]() . Уравнение можно переписать так:
. Уравнение можно переписать так: ![]() , то есть «зет» может быть любым. Что это значит? «Икс» и «игрек» связаны соотношением
, то есть «зет» может быть любым. Что это значит? «Икс» и «игрек» связаны соотношением ![]() , которое прочерчивает в плоскости
, которое прочерчивает в плоскости ![]() некоторую прямую (узнаёте уравнение прямой на плоскости?). Поскольку «зет» может быть любым, то эта прямая «тиражируется» на любой высоте. Таким образом, уравнение
некоторую прямую (узнаёте уравнение прямой на плоскости?). Поскольку «зет» может быть любым, то эта прямая «тиражируется» на любой высоте. Таким образом, уравнение ![]() определяет плоскость, параллельную координатной оси
определяет плоскость, параллельную координатной оси ![]()
Аналогично:
![]() – уравнение плоскости, которая параллельна координатной оси
– уравнение плоскости, которая параллельна координатной оси ![]() ;
;
![]() – уравнение плоскости, которая параллельна координатной оси
– уравнение плоскости, которая параллельна координатной оси ![]() .
.
Если свободные члены ![]() нулевые, то плоскости будут непосредственно проходить через соответствующие оси. Например, классическая «прямая пропорциональность»:
нулевые, то плоскости будут непосредственно проходить через соответствующие оси. Например, классическая «прямая пропорциональность»: ![]() . Начертите в плоскости
. Начертите в плоскости ![]() прямую
прямую ![]() и мысленно размножьте её вверх и вниз (так как «зет» любое). Вывод: плоскость, заданная уравнением
и мысленно размножьте её вверх и вниз (так как «зет» любое). Вывод: плоскость, заданная уравнением ![]() , проходит через координатную ось
, проходит через координатную ось ![]() .
.
Завершаем обзор: плоскость ![]() проходит через начало координат. Ну, здесь совершенно очевидно, что точка
проходит через начало координат. Ну, здесь совершенно очевидно, что точка ![]() удовлетворяет данному уравнению.
удовлетворяет данному уравнению.
И, наконец, случай, который изображён на чертеже: ![]() – плоскость дружит со всеми координатными осями, при этом она всегда «отсекает» треугольник, который может располагаться в любом из восьми октантов.
– плоскость дружит со всеми координатными осями, при этом она всегда «отсекает» треугольник, который может располагаться в любом из восьми октантов.
Как грамотно построить перечисленные виды плоскостей на клетчатой бумаге – смотрите в справочных материалах о пространственных поверхностях.
Линейные неравенства в пространстве
Для лучшего понимания информации желательно хорошо изучить линейные неравенства на плоскости, поскольку многие вещи буду похожи. Параграф будет носить краткий обзорный характер с несколькими примерами, так как материал на практике встречается довольно редко.
Если уравнение ![]() задаёт плоскость, то неравенства
задаёт плоскость, то неравенства
![]() задают полупространства. Если неравенство нестрогое (два последних в списке), то в решение неравенства кроме полупространства входит и сама плоскость.
задают полупространства. Если неравенство нестрогое (два последних в списке), то в решение неравенства кроме полупространства входит и сама плоскость.
Как и для линейных неравенств плоскости, справедлив аналогичный принцип: если одна точка полупространства удовлетворяет неравенству, то и ВСЕ точки данного полупространства удовлетворяют данному неравенству.
Читайте примеры и посматривайте на чертёж:
1) ![]() . Как понимать данное неравенство? «Икс» и «зет» могут быть любыми, а вот «игрек» всегда больше либо равно нулю. Данное неравенство определяет правое полупространство; так как оно нестрогое, то координатная плоскость
. Как понимать данное неравенство? «Икс» и «зет» могут быть любыми, а вот «игрек» всегда больше либо равно нулю. Данное неравенство определяет правое полупространство; так как оно нестрогое, то координатная плоскость ![]() входит в решение.
входит в решение.
2) ![]() – «игрек» и «зет» могут быть любыми, а вот «икс» строго меньше нуля. Неравенство задаёт дальнее от нас полупространство, и ввиду его строгости, координатная плоскость
– «игрек» и «зет» могут быть любыми, а вот «икс» строго меньше нуля. Неравенство задаёт дальнее от нас полупространство, и ввиду его строгости, координатная плоскость ![]() не входит в решение.
не входит в решение.
3) ![]() Сначала мысленно начертим плоскость
Сначала мысленно начертим плоскость ![]() – данная плоскость параллельна «родной» координатной плоскости
– данная плоскость параллельна «родной» координатной плоскости ![]() и расположена на высоте
и расположена на высоте ![]() (на 2 единицы выше плоскости
(на 2 единицы выше плоскости ![]() ). При любых «икс» и «игрек» – «зет» меньше либо равно двум. Поэтому неравенство определяет нижнее полупространство + саму плоскость
). При любых «икс» и «игрек» – «зет» меньше либо равно двум. Поэтому неравенство определяет нижнее полупространство + саму плоскость ![]() .
.
4) Дана плоскость ![]() . Я специально подобрал плоскость, которая «высекает» треугольник в первом октанте (такой, как на чертеже). Требуется строгим неравенством задать полупространство, которое содержит начало координат.
. Я специально подобрал плоскость, которая «высекает» треугольник в первом октанте (такой, как на чертеже). Требуется строгим неравенством задать полупространство, которое содержит начало координат.
Составим вспомогательный многочлен ![]() и вычислим его значение в начале координат:
и вычислим его значение в начале координат: ![]() , таким образом, искомое неравенство:
, таким образом, искомое неравенство: ![]() .
.
Проведённый обзор полезен не только в аналитической геометрии, но и для решения ряда задач математического анализа.
Как составить уравнение плоскости?
Конструировать уравнение плоскости будем с помощью векторов и точек. Их должно быть как можно меньше, но достаточно, чтобы однозначно определить плоскость. Одним словом, красивая математическая лаконичность. Математика – царица наук, не стерва, но строгА. А уж насколько доступна, во многом зависит от вашего к ней отношения =)
Казалось бы, плоскость можно определить с помощью двух неколлинеарных векторов. Но векторы свободны и бродят по всему пространству, поэтому ещё нужна фиксированная точка.
Как составить уравнение плоскости по точке и двум неколлинеарным векторам?
Рассмотрим точку ![]() и два неколлинеарных вектора
и два неколлинеарных вектора ![]() . Уравнение плоскости, которая проходит через точку
. Уравнение плоскости, которая проходит через точку ![]() параллельно векторам
параллельно векторам ![]() , выражается формулой:
, выражается формулой:
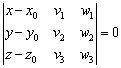
! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.
Принципиально ситуация выглядит так:
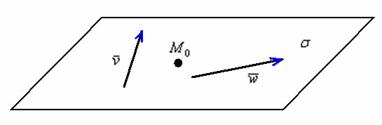
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость однозначно (векторы будут свободно «вертеться» вокруг точки и зададут бесконечно много плоскостей).
Пример 1
Составить уравнение плоскости по точке ![]() и векторам
и векторам ![]() .
.
Решение: Составим уравнение плоскости по точке и двум неколлинеарным векторам:
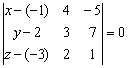
Определитель удобнее всего раскрыть по первому столбцу:
![]()
Раскрываем определители второго порядка:
![]()
На первом месте у нас находится знак «минус». Хорошим тоном считается убрать наглеца, в этих целях меняем знак у каждого слагаемого. Проводим дальнейшие упрощения и получаем уравнение плоскости:
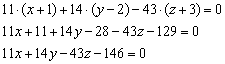
Сократить здесь ничего нельзя, поэтому:
Ответ: ![]()
…числа, конечно, страшноваты получились для первого примера =) …но переделывать, пожалуй, не буду, на практике большие числа – вещь распространённая.
Как проверить задание? Для проверки пока не хватает информации, но я обязательно выполню её чуть позже.
Пример 2
Составить уравнение плоскости по точке ![]() и двум неколлинеарным векторам
и двум неколлинеарным векторам ![]() .
.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Иногда может потребоваться решить обратную задачу – по известному уравнению плоскости найти параллельные ей векторы. Кстати, сколько параллельных векторов существует у плоскости? Бесконечно много. Однако нельзя объять необъятное, поэтому «вытащим» из уравнения плоскости три таких вектора:
Пусть плоскость задана общим уравнением ![]() . Тогда векторы
. Тогда векторы ![]() будут параллельны данной плоскости (а, значит, компланарны), и любые два из них – линейно независимы. Так, в Примере № 1 мы составили уравнение плоскости
будут параллельны данной плоскости (а, значит, компланарны), и любые два из них – линейно независимы. Так, в Примере № 1 мы составили уравнение плоскости ![]() . Построенной плоскости будут параллельны следующие векторы:
. Построенной плоскости будут параллельны следующие векторы: ![]() . Если честно, не припомню, чтобы приходилось этим пользоваться, тем не менее, справка не лишняя.
. Если честно, не припомню, чтобы приходилось этим пользоваться, тем не менее, справка не лишняя.
Итак, «конструкция» из двух неколлинеарных векторов и точки однозначно определяет плоскость. Но существует более очевидный способ, о котором упоминалось выше, и он громким стуком в дверь уже давно просится на урок. Три точки. Дёшево и сердито.
Как составить уравнение плоскости по трём точкам?
Любые ли три точки пространства задают плоскость? Нет. Во-первых, точки должны быть различными. А во-вторых, они не должны лежать на одной прямой (сразу все три).
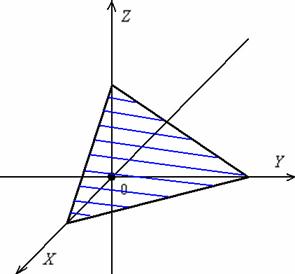
Уравнение плоскости, проходящей через три различные точки ![]() , которые не лежат на одной прямой, можно составить по формуле:
, которые не лежат на одной прямой, можно составить по формуле:
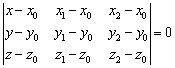
На самом деле это разновидность предыдущего способа, смотрим на картинку:
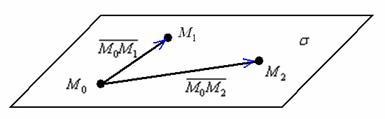
Если известны три различные точки, не лежащие на одной прямой, то легко найти два неколлинеарных вектора, параллельных данной плоскости:
![]()
То есть, наша формула фактически совпадает с формулой предыдущего параграфа. Многие уже заметили явную аналогию с материалами статьи Уравнение прямой на плоскости. Закономерности будут сохраняться и дальше!
Чтобы не умереть от скуки, предлагаю раскрутить примеры-шарады:
Пример 3
Составить уравнение плоскости по точкам ![]() .
.
Решение: составим уравнение плоскости по трём точкам. Используем формулу:
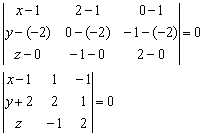
Вот теперь и аналитически видно, что всё дело свелось к координатам двух векторов. Раскрываем определитель по первому столбцу, находим уравнение плоскости:
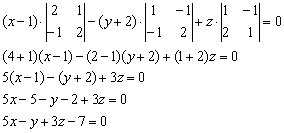
Больше ничего упростить нельзя, записываем:
Ответ: ![]()
Проверка напрашивается сама собой – в полученное уравнение плоскости нужно подставить координаты каждой точки. Если хотя бы одна из трёх точек «не подойдёт», ищите ошибку.
Для «мёртвого» зачёта всегда выполняйте проверку мысленно или на черновике!!!
Пример 4
Составить уравнение плоскости, проходящей через точки ![]() и начало координат.
и начало координат.
Это пример для самостоятельного решения. Ещё раз присмотримся к формуле 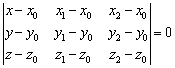 . В каждом столбце определителя встречаются координаты точки
. В каждом столбце определителя встречаются координаты точки ![]() , и это можно с выгодой использовать. В предложенной задаче даны три точки:
, и это можно с выгодой использовать. В предложенной задаче даны три точки: ![]() , начало координат. В качестве точки
, начало координат. В качестве точки ![]() можно выбрать любую из трёх точек. Подумайте, как рациональнее оформить решение! Да, и постарайтесь, не пропускать это задание, в самом конце решения увидите важный технический нюанс ;-)
можно выбрать любую из трёх точек. Подумайте, как рациональнее оформить решение! Да, и постарайтесь, не пропускать это задание, в самом конце решения увидите важный технический нюанс ;-)
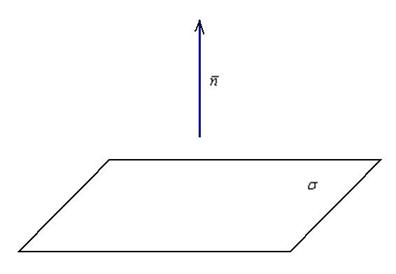
Вектор нормали плоскости (нормальный вектор)
Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов. Но для решения задач нам будет хватать и одного.
Если плоскость задана общим уравнением ![]() , то вектор
, то вектор ![]() является вектором нормали данной плоскости. Просто до безобразия. Всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости.
является вектором нормали данной плоскости. Просто до безобразия. Всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости.
Обещанного три экрана ждут, вернёмся к Примеру № 1 и выполним его проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке ![]() и двум векторам
и двум векторам ![]() . В результате решения мы получили уравнение
. В результате решения мы получили уравнение ![]() . Проверяем:
. Проверяем:
Во-первых, подставим координаты точки ![]() в полученное уравнение:
в полученное уравнение:
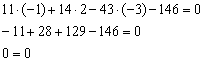
Получено верное равенство, значит, точка ![]() действительно лежит в данной плоскости.
действительно лежит в данной плоскости.
Во-вторых, из уравнения плоскости снимаем вектор нормали: ![]() . Поскольку векторы
. Поскольку векторы ![]() параллельны плоскости, а вектор
параллельны плоскости, а вектор ![]() перпендикулярен плоскости, то должны иметь место следующие факты:
перпендикулярен плоскости, то должны иметь место следующие факты: ![]() . Перпендикулярность векторов легко проверить с помощью скалярного произведения:
. Перпендикулярность векторов легко проверить с помощью скалярного произведения:
![]()
Вывод: уравнение плоскости найдено правильно.
В ходе проверки я фактически процитировал следующее утверждение теории: вектор ![]() параллелен плоскости
параллелен плоскости ![]() в том и только том случае, когда
в том и только том случае, когда ![]() .
.
Решим важную задачу, которая имеет отношение и к уроку Скалярное произведение векторов:
Пример 5
Найти единичный нормальный вектор плоскости ![]() .
.
Решение: Единичный вектор – это вектор, длина которого равна единице. Обозначим данный вектор через ![]() . Совершенно понятно, что векторы
. Совершенно понятно, что векторы ![]() коллинеарны:
коллинеарны:
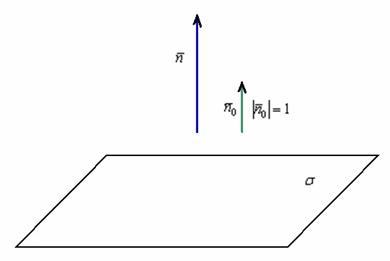
Сначала из уравнения плоскости снимем вектор нормали: ![]() .
.
Как найти единичный вектор? Для того чтобы найти единичный вектор ![]() , нужно каждую координату вектора
, нужно каждую координату вектора ![]() разделить на длину вектора
разделить на длину вектора ![]() .
.
Перепишем вектор нормали в виде ![]() и найдём его длину:
и найдём его длину:
![]()
Согласно вышесказанному:
![]()
Ответ: ![]()
Проверка: 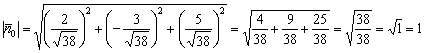 , что и требовалось проверить.
, что и требовалось проверить.
Читатели, которые внимательно изучили последний параграф урока Скалярное произведение векторов, наверное, заметили, что координаты единичного вектора ![]() – это в точности направляющие косинусы вектора
– это в точности направляющие косинусы вектора ![]() :
:
![]()
Отвлечёмся от разобранной задачи: когда вам дан произвольный ненулевой вектор, и по условию требуется найти его направляющие косинусы (см. последние задачи урока Скалярное произведение векторов), то вы, по сути, находите и единичный вектор, коллинеарный данному. Фактически два задания в одном флаконе.
Необходимость найти единичный вектор нормали возникает в некоторых задачах математического анализа.
С выуживанием нормального вектора разобрались, теперь ответим на противоположный вопрос:
Как составить уравнение плоскости по точке и вектору нормали?
Эту жёсткую конструкцию вектора нормали и точки хорошо знает мишень для игры в дартс. Пожалуйста, вытяните руку вперёд и мысленно выберите произвольную точку пространства, например, маленькую кошечку в серванте. Очевидно, что через данную точку можно провести единственную плоскость, перпендикулярную вашей руке.
Уравнение плоскости, проходящей через точку ![]() перпендикулярно вектору
перпендикулярно вектору ![]() , выражается формулой:
, выражается формулой:
![]()
Выглядит значительно привлекательнее, чем предыдущие мытарства. В некоторых задачах аналитической геометрии уравнение плоскости можно составить несколькими способами, и решение через точку и нормальный вектор – самое оптимальное.
Пример 6
Составить уравнение плоскости по точке ![]() и вектору нормали
и вектору нормали ![]() .
.
Решение: Используем формулу:
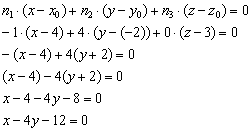
Ответ: ![]()
Проверка выполняется очень легко:
1) Из полученного уравнения ![]() снимаем вектор нормали:
снимаем вектор нормали: ![]() – всё хорошо, полученный вектор совпал с вектором из условия (в ряде случаев может получиться коллинеарный вектор).
– всё хорошо, полученный вектор совпал с вектором из условия (в ряде случаев может получиться коллинеарный вектор).
2) Подставим координаты точки ![]() в уравнение плоскости:
в уравнение плоскости:
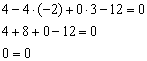
Верное равенство, значит, точка ![]() принадлежит данной плоскости.
принадлежит данной плоскости.
Вывод: уравнение плоскости найдено правильно.
Пример настолько прозрачен, что хочется немного завуалировать условие:
Пример 7
Найти уравнение плоскости, проходящей через точку ![]() перпендикулярно оси
перпендикулярно оси ![]() .
.
Это пример для самостоятельного решения. Просто, но со вкусом.
Перейдём к более содержательным примерам. Типовая задача:
Как построить плоскость, параллельную данной?
Пример 8
Построить плоскость, проходящую через точку ![]() параллельно плоскости
параллельно плоскости ![]() .
.
Решение: Обозначим известную плоскость через ![]() . По условию требуется найти плоскость
. По условию требуется найти плоскость ![]() , которая параллельна плоскости
, которая параллельна плоскости ![]() и проходит через точку
и проходит через точку ![]() .
.
Выполним схематический чертёж, который поможет быстрее разобраться в условии и понять алгоритм решения:
У параллельных плоскостей один и тот же вектор нормали. Добавить нечего =) Осталось оформить мат в два хода:
1) Из уравнения ![]() найдём вектор нормали плоскости:
найдём вектор нормали плоскости: ![]() .
.
2) Уравнение плоскости ![]() составим по точке
составим по точке ![]() и вектору нормали
и вектору нормали ![]() :
:
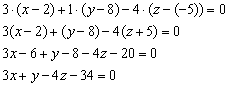
Ответ: ![]()
Как выполнить проверку, я уже рассказал.
Продолжаем раскидывать стог сена пространственной геометрии:
Как найти расстояние от точки до плоскости?
Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из точки ![]() к данной плоскости:
к данной плоскости:
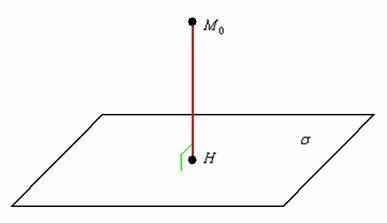
Формула очень похожа на формулу «плоской» геометрии расстояния от точки до прямой (см. Пример № 8 урока Простейшие задачи с прямой на плоскости).
Расстояние от точки ![]() до плоскости
до плоскости ![]() выражается формулой
выражается формулой
![]()
При желании или надобности можно найти и точку ![]() , но для этого нужно разобраться с уравнениями прямой в пространстве и посетить урок Основные задачи на прямую и плоскость.
, но для этого нужно разобраться с уравнениями прямой в пространстве и посетить урок Основные задачи на прямую и плоскость.
Пример 9
Найти расстояние от точки ![]() до плоскости
до плоскости ![]()
Решение: анализировать тут нечего, главное, не допустить ошибку в вычислениях:
![]()
Ответ: ![]()
Такое даже для самостоятельного решения неловко предлагать.
Заключительный раздел урока будет посвящен взаимному расположению плоскостей. Мы уже немного поговорили о параллельных плоскостях, и сейчас продолжим тему:
Взаимное расположение плоскостей
Для практики наиболее важна информация о взаимном расположении двух плоскостей, но и о трёх плоскостях также будет краткая справка.
Рассмотрим две плоскости пространства, заданные общими уравнениями:
![]()
Они могут:
1) совпадать;
2) быть параллельными: ![]() ;
;
3) пересекаться по некоторой прямой «эль»: ![]() .
.
Всё очень и очень похоже на взаимное расположение прямых на плоскости (урок Простейшие задачи с прямой на плоскости).
Совпадающие плоскости
Две плоскости совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства ![]()
Рассмотрим плоскости ![]() и составим систему:
и составим систему:
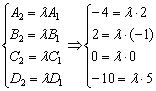
Из каждого уравнения системы следует, что ![]() . Таким образом, система совместна и плоскости
. Таким образом, система совместна и плоскости ![]() совпадают.
совпадают.
Параллельные плоскости
Две плоскости параллельны тогда и только тогда, когда их коэффициенты при переменных ![]() пропорциональны:
пропорциональны: ![]() , но
, но ![]() .
.
На практике очень часто первые три коэффициента банально совпадают (![]() ). Посмотрим, например, на уравнения параллельных плоскостей из Примера № 8:
). Посмотрим, например, на уравнения параллельных плоскостей из Примера № 8:
![]()
Комментарии, думаю, излишни, всё прекрасно видно. Но на всякий случай выполню формальную проверку, вдруг кому потребуется. Составим систему:
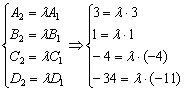
Из первых трёх уравнений следует, что ![]() , а из четвёртого уравнения следует, что
, а из четвёртого уравнения следует, что ![]() , значит, система несовместна. Но коэффициенты при переменных
, значит, система несовместна. Но коэффициенты при переменных ![]() пропорциональны, следовательно, плоскости параллельны.
пропорциональны, следовательно, плоскости параллельны.
Задача о нахождении параллельной плоскости уже была, поэтому решим что-нибудь новое:
Как найти расстояние между плоскостями?
Расстояние между двумя параллельными плоскостями ![]() выражается формулой:
выражается формулой:
![]()
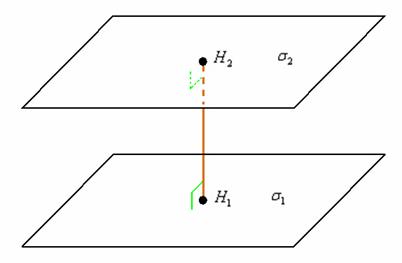
Координаты точек ![]() нам неизвестны, да их и не нужно знать, поскольку перпендикуляр между плоскостями можно протянуть в любом месте.
нам неизвестны, да их и не нужно знать, поскольку перпендикуляр между плоскостями можно протянуть в любом месте.
Найдём расстояние между параллельными плоскостями Примера № 8:
Пример 10
Найти расстояние между параллельными плоскостями ![]() .
.
Решение: Используем формулу:
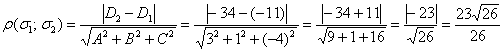
Ответ: ![]()
У многих наверняка возник вопрос: вот у этих плоскостей ![]() – первые три коэффициенты одинаковы, но это же не всегда так! Да, не всегда.
– первые три коэффициенты одинаковы, но это же не всегда так! Да, не всегда.
Пример 11
Найти расстояние между параллельными плоскостями ![]()
Проверим пропорциональность коэффициентов: ![]() , но
, но ![]() , значит, плоскости действительно параллельны. Первые три коэффициента пропорциональны, но не совпадают. Однако формула-то
, значит, плоскости действительно параллельны. Первые три коэффициента пропорциональны, но не совпадают. Однако формула-то ![]() предусмотрена для совпадающих коэффициентов!
предусмотрена для совпадающих коэффициентов!
Есть два пути решения:
1) Найдём какую-нибудь точку, принадлежащую любой из плоскостей. Например, рассмотрим плоскость ![]() . Чтобы найти точку, проще всего обнулить две координаты. Обнулим «икс» и «зет», тогда:
. Чтобы найти точку, проще всего обнулить две координаты. Обнулим «икс» и «зет», тогда: ![]() .
.
Таким образом, точка ![]() принадлежит данной плоскости. Теперь можно использовать формулу расстояния от точки до плоскости
принадлежит данной плоскости. Теперь можно использовать формулу расстояния от точки до плоскости ![]() , рассмотренную в предыдущем разделе.
, рассмотренную в предыдущем разделе.
2) Второй способ связан с небольшим трюком, который нужно применить, чтобы таки использовать формулу ![]() ! Это пример для самостоятельного решения.
! Это пример для самостоятельного решения.
Пересекающиеся плоскости
Третий, самый распространённый случай, когда две плоскости пересекаются по некоторой прямой ![]() :
:
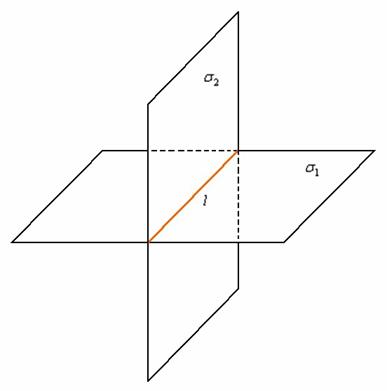
Две плоскости пересекаются тогда и только тогда, когда их коэффициенты при переменных ![]() НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства
НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства ![]()
Сразу отмечу важный факт: Если плоскости пересекаются, то система линейных уравнений ![]() задаёт прямую в пространстве. Но о ней позже.
задаёт прямую в пространстве. Но о ней позже.
В качестве примера рассмотрим плоскости ![]() . Составим систему для соответствующих коэффициентов:
. Составим систему для соответствующих коэффициентов:
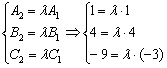
Из первых двух уравнений следует, что ![]() , но из третьего уравнения следует, что
, но из третьего уравнения следует, что ![]() , значит, система несовместна, и плоскости пересекаются.
, значит, система несовместна, и плоскости пересекаются.
Проверку можно выполнить «по пижонски» одной строкой:
![]()
Параллельные плоскости мы уже разобрали, теперь поговорим о перпендикулярных плоскостях. Очевидно, что к любой плоскости можно провести бесконечно много перпендикулярных плоскостей, а для того, чтобы зафиксировать конкретную перпендикулярную плоскость, нужно задать две точки:
Пример 12
Дана плоскость ![]() . Построить плоскость
. Построить плоскость ![]() , перпендикулярную данной и проходящую через точки
, перпендикулярную данной и проходящую через точки ![]() .
.
Решение: Начинаем анализировать условие. Что мы знаем о плоскости ![]() ? Известны две точки. Можно найти вектор
? Известны две точки. Можно найти вектор ![]() , параллельный данной плоскости. Но этого мало, нужен ещё один. Так как плоскости должны быть перпендикулярны, то вторым вектором следует взять нормальный вектор плоскости
, параллельный данной плоскости. Но этого мало, нужен ещё один. Так как плоскости должны быть перпендикулярны, то вторым вектором следует взять нормальный вектор плоскости ![]() .
.
Проводить подобные рассуждения здОрово помогает схематический чертёж:
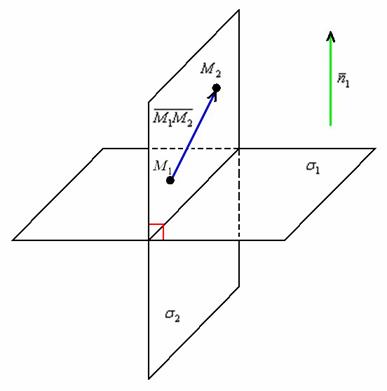
Для лучшего понимания задачи отложите вектор нормали ![]() от точки
от точки ![]() в плоскости
в плоскости ![]() .
.
Кстати, теперь чётко видно, почему одна точка не определит перпендикулярную плоскость – вокруг единственной точки будет «вращаться» бесконечно много перпендикулярных плоскостей. Так же нас не устроит и единственный вектор (без всяких точек). Вектор является свободным и «наштампует» нам бесконечно много перпендикулярных плоскостей (которые, к слову, будут параллельны между собой). В этой связи минимальную жёсткую конструкцию обеспечивают две точки.
Задача разобрана, решаем:
1) Найдём вектор ![]() .
.
2) Из уравнения ![]() снимем вектор нормали:
снимем вектор нормали: ![]() .
.
3) Уравнение плоскости ![]() составим по точке
составим по точке ![]() (можно было взять и
(можно было взять и ![]() ) и двум неколлинеарным векторам
) и двум неколлинеарным векторам ![]() :
:
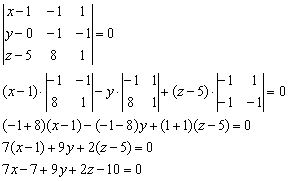
Ответ: ![]()
Проверка состоит из двух этапов:
1) Проверяем, действительно ли плоскости будут перпендикулярны. Если две плоскости перпендикулярны, то их векторы нормали будут ортогональны. Логично. Из полученного уравнения ![]() снимаем вектор нормали
снимаем вектор нормали ![]() и рассчитываем скалярное произведение векторов:
и рассчитываем скалярное произведение векторов:
![]()
Таким образом, ![]()
2) В уравнение плоскости ![]() подставляем координаты точек
подставляем координаты точек ![]() . Обе точки должны «подойти».
. Обе точки должны «подойти».
И первый, и второй пункт можно выполнить устно.
Перейдём к заключительной задаче урока:
Как найти угол между плоскостями?
Две пересекающиеся плоскости ![]() образуют четыре двухгранных угла и любой из этих углов называют углом между плоскостями.
образуют четыре двухгранных угла и любой из этих углов называют углом между плоскостями.
Обозначим угол между плоскостями через ![]() :
:
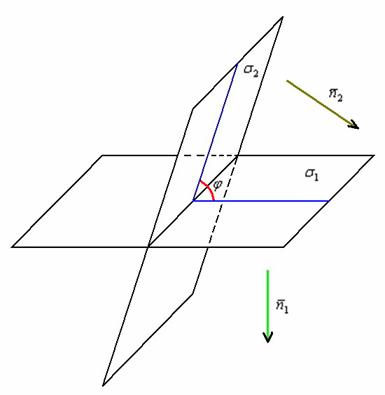
Наклон плоскости однозначно определяется её вектором нормали, поэтому угол между плоскостями можно найти через угол между нормальными векторами данных плоскостей. А угол между векторами рассчитывается с помощью обыденной формулы, рассмотренной на уроке Скалярное произведение векторов:
![]()
Распишем формулу в коэффициентах:
![]()
Обратите внимание, что формула может дать и тупой угол, например, 150 градусов. Такой ответ не будет страшной ошибкой, но за угол между плоскостями, как правило, принимают острый угол, поэтому концовку задания лучше дополнить расчётом «традиционного» угла: 180 – 150 =30 градусов.
Задачка поинтереснее:
Пример 13
Найти угол между плоскостями ![]()
Это пример для самостоятельного решения. Решение и ответ в конце урока.
Что-то не хочется мне вас сегодня отпускать… наверное, хорошо себя вели и активно работали на уроке =) Придётся рассказать что-нибудь ещё.
Взаимное расположение трёх плоскостей
Три плоскости могут располагаться в пространстве 8 способами, если интересуют все случаи, пожалуйста, посмотрите в книге Атанасяна-Базылева или в Интернете, видел вроде в Википедии, точно уже не помню.
Самый известный случай взаимного расположения трёх плоскостей – плоскости пересекаются в одной точке. Живой пример находится совсем недалеко от вас. Посмотрите вверх – в угол комнаты, где пересекаются две стены и потолок. Пессимисты могут посмотреть вниз.
Аналитически данному случаю соответствует система линейных уравнений 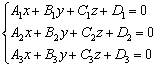 , которая имеет единственное решение.
, которая имеет единственное решение.
Ничего не напоминает? Вот, оказывается, где прячется метод Крамера… – в углу вашей комнаты!
На следующем уроке мы изучим Прямые в пространстве.
Спасибо за работу, домашнего задания не будет!
Решения и ответы:
Пример 2: Решение: составим уравнение плоскости по точке и двум неколлинеарным векторам:
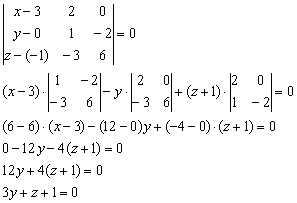
Ответ: ![]()
Пример 4: Решение: составим уравнение плоскости по трём точкам ![]() :
:
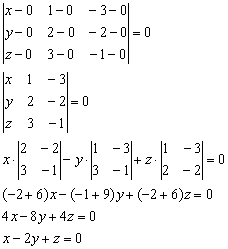
Ответ: ![]()
Пример 7: Решение: Так как плоскость перпендикулярна оси ![]() , то вектор
, то вектор ![]() является вектором нормали для данной плоскости. Уравнение плоскости составим по точке
является вектором нормали для данной плоскости. Уравнение плоскости составим по точке ![]() и вектору нормали
и вектору нормали ![]() :
:
![]()
Ответ: ![]()
Пример 11: Решение: Разделим все коэффициенты второго уравнения на два:
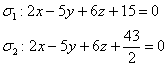
Используем формулу
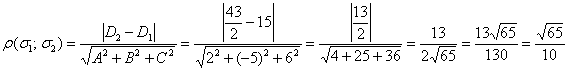
Ответ: ![]()
Пример 13: Решение: Обозначим ![]() . Используем формулу:
. Используем формулу:
![]()
![]()
За угол между плоскостями примем острый угол: ![]()
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
