
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Линейная зависимость и линейная независимость векторов.
Базис векторов. Аффинная система координат
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.
Линейная зависимость векторов, линейная независимость векторов, базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл. Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства ![]() . Или вектор погоды, за которым я только что сходил на Гисметео:
. Или вектор погоды, за которым я только что сходил на Гисметео: ![]() – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
– температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всем векторам с алгебраической точки зрения, но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры. Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Линейная зависимость и независимость векторов плоскости.
Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости. Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор ![]() . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор
. Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор ![]() . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах
. Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах ![]() ? Данные векторы коллинеарны, а значит, линейно выражаются друг через друга:
? Данные векторы коллинеарны, а значит, линейно выражаются друг через друга:
![]() , ну, или наоборот:
, ну, или наоборот: ![]() , где
, где ![]() – некоторое число, отличное от нуля.
– некоторое число, отличное от нуля.
Картинку сего действа можно посмотреть на уроке Векторы для чайников, где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики ![]() задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина.
задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина.
Такие векторы называют линейно зависимыми.
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны.
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости ![]() линейно независимы в том и только том случае, если они не коллинеарны. Итак, базис
линейно независимы в том и только том случае, если они не коллинеарны. Итак, базис ![]() получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
Любой вектор плоскости ![]() единственным образом раскладывается по базису
единственным образом раскладывается по базису ![]() :
:
![]() , где
, где ![]() – действительные числа. Числа
– действительные числа. Числа ![]() называют координатами вектора в данном базисе.
называют координатами вектора в данном базисе.
Также говорят, что вектор ![]() представлен в виде линейной комбинации базисных векторов. То есть, выражение
представлен в виде линейной комбинации базисных векторов. То есть, выражение ![]() называют разложением вектора
называют разложением вектора ![]() по базису
по базису ![]() или линейной комбинацией базисных векторов.
или линейной комбинацией базисных векторов.
Например, можно сказать, что вектор ![]() разложен по ортонормированному базису плоскости
разложен по ортонормированному базису плоскости ![]() , а можно сказать, что он представлен в виде линейной комбинации векторов
, а можно сказать, что он представлен в виде линейной комбинации векторов ![]() .
.
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов ![]() , взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.
, взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке. Базисы ![]() – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
– это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом ![]() . Вот стандартная картина:
. Вот стандартная картина:
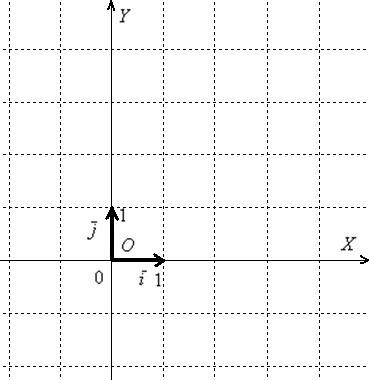
Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис ![]() . И это почти так. Формулировка звучит следующим образом:
. И это почти так. Формулировка звучит следующим образом:
Точка ![]() плоскости, которая называется началом координат, и ортонормированный базис
плоскости, которая называется началом координат, и ортонормированный базис ![]() задают декартову прямоугольную систему координат плоскости. То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами
задают декартову прямоугольную систему координат плоскости. То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами ![]() . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
. Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
Думаю, всем понятно, что с помощью точки ![]() (начала координат) и ортонормированного базиса
(начала координат) и ортонормированного базиса ![]() ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».
ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку ![]() и два ортогональных вектора
и два ортогональных вектора ![]() произвольной ненулевой длины:
произвольной ненулевой длины:
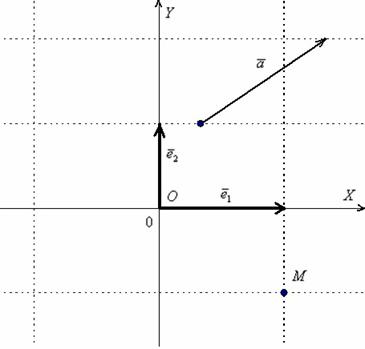
Такой базис называется ортогональным. Начало координат с векторами ![]() задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например,
задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, ![]() или
или ![]() . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
. Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
! Примечание: в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ. Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными. Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка ![]() плоскости, которая называется началом координат, и неколлинеарные векторы
плоскости, которая называется началом координат, и неколлинеарные векторы ![]() , взятые в определённом порядке, задают аффинную систему координат плоскости:
, взятые в определённом порядке, задают аффинную систему координат плоскости:
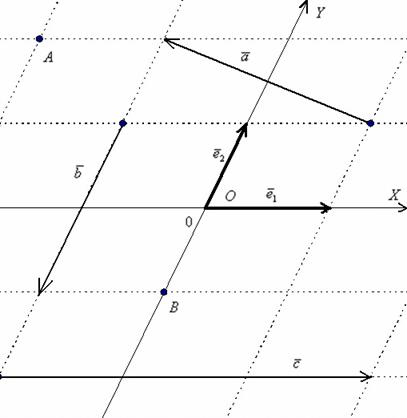
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки ![]() и векторы:
и векторы:
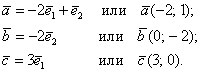
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников, многие вкусные формулы, связанные со скалярным произведением векторов. Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении, а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Как определить коллинеарность векторов плоскости?
Типовая вещь. Для того чтобы два вектора плоскости ![]() были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны
были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны 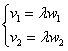 . По существу, это покоординатная детализация очевидного соотношения
. По существу, это покоординатная детализация очевидного соотношения ![]() .
.
Пример 1
а) Проверить, коллинеарны ли векторы ![]() .
.
б) Образуют ли базис векторы ![]() ?
?
Решение:
а) Выясним, существует ли для векторов ![]() коэффициент пропорциональности
коэффициент пропорциональности ![]() , такой, чтобы выполнялись равенства
, такой, чтобы выполнялись равенства 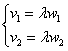 :
:
![]() , значит, данные векторы коллинеарны.
, значит, данные векторы коллинеарны.
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию ![]() и посмотреть, будет ли она верной:
и посмотреть, будет ли она верной:
Составим пропорцию из отношений соответствующих координат векторов:
![]()
Сокращаем:
![]() , таким образом, соответствующие координаты пропорциональны, следовательно,
, таким образом, соответствующие координаты пропорциональны, следовательно, ![]()
Отношение можно было составить и наоборот, это равноценный вариант:
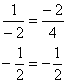
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства ![]() . Их справедливость легко проверяется через элементарные действия с векторами:
. Их справедливость легко проверяется через элементарные действия с векторами:
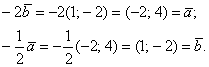
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы ![]() . Составим систему:
. Составим систему:
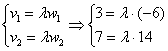
Из первого уравнения следует, что ![]() , из второго уравнения следует, что
, из второго уравнения следует, что ![]() , значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.
, значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.
Вывод: векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов ![]() :
:
![]() , значит, данные векторы линейно независимы и образуют базис.
, значит, данные векторы линейно независимы и образуют базис.
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: ![]() . Или так:
. Или так: ![]() . Или так:
. Или так: ![]() . Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».
. Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».
Ответ: а) ![]() , б) образуют.
, б) образуют.
Небольшой творческий пример для самостоятельного решения:
Пример 2
При каком значении параметра ![]() векторы
векторы ![]() будут коллинеарны?
будут коллинеарны?
В образце решения параметр найден через пропорцию ![]() .
.
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не коллинеарны;
4) векторы нельзя линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля.
Соответственно, эквивалентны следующие противоположные утверждения:
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю.
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости ![]() коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю:
коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: 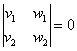 . Для применения данного признака, естественно, нужно уметь находить определители.
. Для применения данного признака, естественно, нужно уметь находить определители.
Решим Пример 1 вторым способом:
а) Вычислим определитель, составленный из координат векторов ![]() :
:
![]() , значит, данные векторы коллинеарны.
, значит, данные векторы коллинеарны.
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов ![]() :
:
![]() , значит, векторы
, значит, векторы ![]() линейно независимы и образуют базис.
линейно независимы и образуют базис.
Ответ: а) ![]() , б) образуют.
, б) образуют.
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
Проверка векторов на коллинеарность – простая и очень распространенная задача аналитической геометрии. Нередко в условии заодно требуется проверить векторы и на ортогональность (базис в таких случаях, как правило, ортонормированный). Данное задание подробно рассмотрено на уроке Скалярное произведение векторов.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Пример 3
Даны вершины четырёхугольника ![]() . Доказать, что четырёхугольник
. Доказать, что четырёхугольник ![]() является параллелограммом.
является параллелограммом.
Доказательство: Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, нужно доказать:
1) параллельность противоположных сторон ![]() и
и ![]() ;
;
2) параллельность противоположных сторон ![]() и
и ![]() .
.
Доказываем:
1) Найдём векторы:
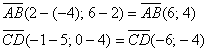
Вычислим определитель, составленный из координат векторов ![]() :
:
![]() , значит, данные векторы коллинеарны, и
, значит, данные векторы коллинеарны, и ![]() .
.
2) Найдём векторы:
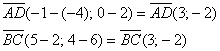
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов ![]() :
:
![]() , значит, данные векторы коллинеарны, и
, значит, данные векторы коллинеарны, и ![]() .
.
Вывод: Противоположные стороны четырёхугольника ![]() попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать.
попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать.
Больше фигур хороших и разных:
Пример 4
Даны вершины четырёхугольника ![]() . Доказать, что четырёхугольник
. Доказать, что четырёхугольник ![]() является трапецией.
является трапецией.
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?
Правило очень похоже. Для того чтобы два вектора пространства ![]() были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны
были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны 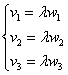 .
.
Пример 5
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) ![]() ;
;
б) ![]()
в) ![]()
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
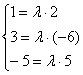
Система не имеет решения, значит, векторы ![]() не коллинеарны.
не коллинеарны.
«Упрощёнка» оформляется проверкой пропорции ![]() . В данном случае:
. В данном случае:
![]() – соответствующие координаты не пропорциональны, значит, векторы
– соответствующие координаты не пропорциональны, значит, векторы ![]() не коллинеарны.
не коллинеарны.
Ответ: векторы ![]() не коллинеарны.
не коллинеарны.
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов.
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства.
Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы ![]() , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
, они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы ![]() мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы
мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы ![]() не коллинеарны, то третий вектор выражается через них единственным образом:
не коллинеарны, то третий вектор выражается через них единственным образом: ![]() (а почему – легко догадаться по материалам предыдущего раздела).
(а почему – легко догадаться по материалам предыдущего раздела).
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов ![]() , взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису
, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису ![]() , где
, где ![]() – координаты вектора
– координаты вектора ![]() в данном базисе
в данном базисе
Напоминаю, также можно сказать, что вектор ![]() представлен в виде линейной комбинации базисных векторов.
представлен в виде линейной комбинации базисных векторов.
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
Точка ![]() пространства, которая называется началом координат, и некомпланарные векторы
пространства, которая называется началом координат, и некомпланарные векторы ![]() , взятые в определённом порядке, задают аффинную систему координат трёхмерного пространства:
, взятые в определённом порядке, задают аффинную систему координат трёхмерного пространства:
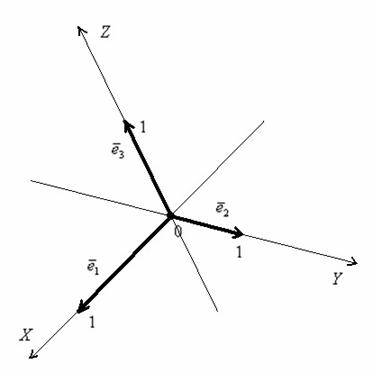
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства:
Точка ![]() пространства, которая называется началом координат, и ортонормированный базис
пространства, которая называется началом координат, и ортонормированный базис ![]() задают декартову прямоугольную систему координат пространства. Знакомая картинка:
задают декартову прямоугольную систему координат пространства. Знакомая картинка:
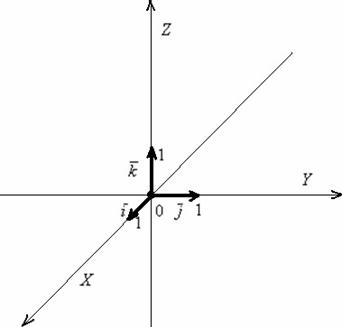
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) ни один из векторов нельзя линейно выразить через другие;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Три вектора пространства ![]() компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю:
компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: 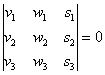 .
.
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Пример 6
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
а) ![]()
б) ![]()
Решение: Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов ![]() (определитель раскрыт по первой строке):
(определитель раскрыт по первой строке):
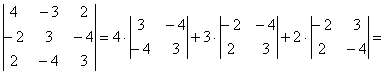
![]() , значит, векторы
, значит, векторы ![]() линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
Ответ: данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
Пример 7
При каком значении параметра ![]() векторы
векторы ![]() будут компланарны?
будут компланарны?
Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
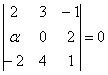
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
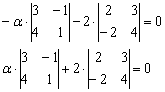
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
![]()
Ответ: при ![]()
Здесь легко выполнить проверку, для этого нужно подставить полученное значение ![]() в исходный определитель и убедиться, что
в исходный определитель и убедиться, что 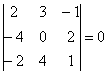 , раскрыв его заново.
, раскрыв его заново.
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространства
и найти координаты 4-го вектора в данном базисе
Пример 8
Даны векторы ![]() . Показать, что векторы
. Показать, что векторы ![]() образуют базис трехмерного пространства и найти координаты вектора
образуют базис трехмерного пространства и найти координаты вектора ![]() в этом базисе.
в этом базисе.
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора ![]() вполне могут образовывать новый базис. И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы
вполне могут образовывать новый базис. И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы ![]() линейно независимы:
линейно независимы:
Вычислим определитель, составленный из координат векторов ![]() :
:
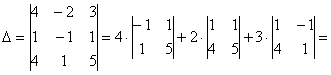
![]() , значит, векторы
, значит, векторы ![]() линейно независимы и образуют базис трехмерного пространства.
линейно независимы и образуют базис трехмерного пространства.
! Важно: координаты векторов ![]() обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Теперь вспомним теоретическую часть: если векторы ![]() образуют базис, то любой вектор
образуют базис, то любой вектор ![]() можно единственным способом разложить по данному базису:
можно единственным способом разложить по данному базису: ![]() , где
, где ![]() – координаты вектора в базисе
– координаты вектора в базисе ![]() .
.
Поскольку наши векторы ![]() образуют базис трёхмерного пространства (это уже доказано), то вектор
образуют базис трёхмерного пространства (это уже доказано), то вектор ![]() можно единственным образом разложить по данному базису:
можно единственным образом разложить по данному базису:
![]() , где
, где ![]() – координаты вектора
– координаты вектора ![]() в базисе
в базисе ![]() .
.
По условию и требуется найти координаты ![]() .
.
Для удобства объяснения поменяю части местами: ![]() . В целях нахождения
. В целях нахождения ![]() следует расписать данное равенство покоординатно:
следует расписать данное равенство покоординатно:
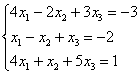
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя 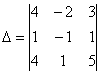 , в правую часть записаны координаты вектора
, в правую часть записаны координаты вектора ![]() .
.
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден:
![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.
Дальнейшее – дело техники:

Таким образом:
![]() – разложение вектора
– разложение вектора ![]() по базису
по базису ![]() .
.
Ответ: ![]()
Более подготовленные читатели могут ознакомиться с уроком Переход к новому базису, и окончательно уяснить смысл прорешанной задачи. Кстати, с содержательной точки зрения использовать метод Крамера здесь – совсем не айс ;-)
И, как я уже отмечал, задание носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, произвольные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу – решение будет технически намного проще, и поэтому я прошёл мимо него в предыдущем параграфе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Пример 9
Даны векторы ![]() . Показать, что векторы
. Показать, что векторы ![]() образуют базис и найти координаты вектора
образуют базис и найти координаты вектора ![]() в этом базисе. Систему линейных уравнений решить методом Крамера.
в этом базисе. Систему линейных уравнений решить методом Крамера.
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра.…Хотя, кто его знает, может быть и не чистая…, однако закругляемся – о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Решения и ответы:
Пример 2: Решение: составим пропорцию из соответствующих координат векторов:
![]()
Ответ: при ![]()
Пример 4: Доказательство: трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон ![]() и
и ![]() .
.
Найдём векторы:
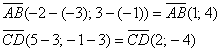
Вычислим определитель, составленный из координат векторов ![]() :
:
![]() , значит, данные векторы не коллинеарны и стороны
, значит, данные векторы не коллинеарны и стороны ![]() не параллельны.
не параллельны.
2) Проверим параллельность противоположных сторон ![]() и
и ![]() .
.
Найдём векторы:
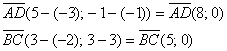
Вычислим определитель, составленный из координат векторов ![]() :
:
![]() , значит, данные векторы коллинеарны и
, значит, данные векторы коллинеарны и ![]() .
.
Вывод: Две стороны четырёхугольника ![]() параллельны, а две другие стороны не параллельны, значит, он является трапецией по определению. Что и требовалось доказать.
параллельны, а две другие стороны не параллельны, значит, он является трапецией по определению. Что и требовалось доказать.
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
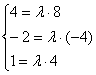
Система не имеет решения, значит, векторы ![]() не коллинеарны.
не коллинеарны.
Более простое оформление:
![]() – вторая и третья координаты не пропорциональны, значит, векторы
– вторая и третья координаты не пропорциональны, значит, векторы ![]() не коллинеарны.
не коллинеарны.
Ответ: векторы ![]() не коллинеарны.
не коллинеарны.
в) Исследуем на коллинеарность векторы ![]() . Составим систему:
. Составим систему:
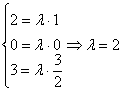
Соответствующие координаты векторов пропорциональны, значит ![]()
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ: ![]()
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов ![]() (определитель раскрыт по первой строке):
(определитель раскрыт по первой строке):
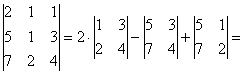
![]() , значит, векторы
, значит, векторы ![]() линейно зависимы и не образуют базиса трёхмерного пространства.
линейно зависимы и не образуют базиса трёхмерного пространства.
Ответ: данные векторы не образуют базиса
Пример 9: Решение: Вычислим определитель, составленный из координат векторов ![]() :
:

Таким образом, векторы ![]() линейно независимы и образуют базис.
линейно независимы и образуют базис.
Представим вектор ![]() в виде линейной комбинации базисных векторов:
в виде линейной комбинации базисных векторов:
![]()
Покоординатно:
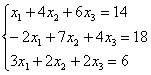
Систему решим по формулам Крамера:
![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.

Ответ: Векторы ![]() образуют базис,
образуют базис, ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
