
Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Форум, библиотека и блог: mathprofi
Форум, библиотека и блог: mathprofi
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi.com
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Что такое производная?
Определение и смысл производной функции
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных.
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции, и, в особенности, бесконечно малые величины. Дело в том, что определение производной базируется на понятии предела, которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций. Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные, в том числе производные сложных функций. Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования, даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной, где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики», пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функции
Многие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу ![]() (вид сбоку):
(вид сбоку):
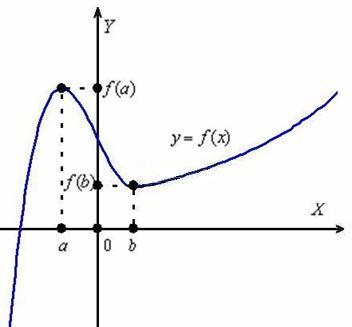
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо. Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах ![]() функция возрастает, то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале
функция возрастает, то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале ![]() функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке ![]() мы достигаем максимума, то есть существует такой участок пути, на котором значение
мы достигаем максимума, то есть существует такой участок пути, на котором значение ![]() будет самым большим (высоким). В точке же
будет самым большим (высоким). В точке же ![]() достигается минимум, и существует такая её окрестность, в которой значение
достигается минимум, и существует такая её окрестность, в которой значение ![]() самое маленькое (низкое).
самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции, а пока изучим ещё одну важную особенность: на промежутках ![]() функция возрастает, но возрастает она с разной скоростью. И первое, что бросается в глаза – на интервале
функция возрастает, но возрастает она с разной скоростью. И первое, что бросается в глаза – на интервале ![]() график взмывает вверх гораздо более круто, чем на интервале
график взмывает вверх гораздо более круто, чем на интервале ![]() . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
. Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Скорость изменения функции
Идея состоит в следующем: возьмём некоторое значение ![]() (читается «дельта икс»), которое назовём приращением аргумента, и начнём его «примерять» к различным точкам нашего пути:
(читается «дельта икс»), которое назовём приращением аргумента, и начнём его «примерять» к различным точкам нашего пути:
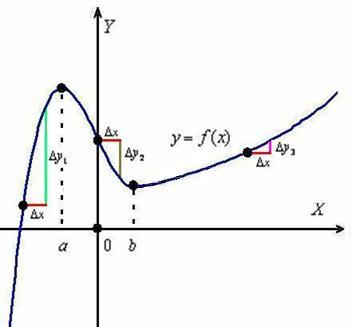
1) Посмотрим на самую левую точку: минуя расстояние ![]() , мы поднимаемся по склону на высоту
, мы поднимаемся по склону на высоту ![]() (зелёная линия). Величина
(зелёная линия). Величина ![]() называется приращением функции, и в данном случае это приращение положительно (разность значений по оси
называется приращением функции, и в данном случае это приращение положительно (разность значений по оси ![]() – больше нуля). Составим отношение
– больше нуля). Составим отношение ![]() , которое и будет мерИлом крутизны нашей дороги. Очевидно, что
, которое и будет мерИлом крутизны нашей дороги. Очевидно, что ![]() – это вполне конкретное число, и, поскольку оба приращения положительны, то
– это вполне конкретное число, и, поскольку оба приращения положительны, то ![]() .
.
Внимание! Обозначение ![]() являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
являются ЕДИНЫМ символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние ![]() метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит
метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит ![]() метров (зелёная линия) и:
метров (зелёная линия) и: ![]() . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
. Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание: числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние ![]() от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение
от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение ![]() (малиновая линия) относительно невелико, и отношение
(малиновая линия) относительно невелико, и отношение ![]() по сравнению с предыдущим случаем будет весьма скромным. Условно говоря,
по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, ![]() метров и скорость роста функции составляет
метров и скорость роста функции составляет ![]() . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
. То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние ![]() , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси
, в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ![]() ), то итоговое приращение функции (высоты) будет отрицательным:
), то итоговое приращение функции (высоты) будет отрицательным: ![]() метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции:
метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: ![]() , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
, то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» ![]() лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом
лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом ![]() мы не получим вразумительной характеристики подобных участков пути посредством отношения
мы не получим вразумительной характеристики подобных участков пути посредством отношения ![]() .
.
Из проведённого рассуждения следует вывод – чем меньше значение ![]() , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
, тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов ![]() можно подобрать значение
можно подобрать значение ![]() (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты
(пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты ![]() будет гарантированно положительным, и неравенство
будет гарантированно положительным, и неравенство ![]() корректно укажет рост функции в каждой точке этих интервалов.
корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона ![]() существует значение
существует значение ![]() , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты
, которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты ![]() однозначно отрицательно, и неравенство
однозначно отрицательно, и неравенство ![]() корректно покажет убыль функции в каждой точке данного интервала.
корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: ![]() . Во-первых, нулевое приращение высоты (
. Во-первых, нулевое приращение высоты (![]() ) – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок
) – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок ![]() в любую сторону, то изменение высоты
в любую сторону, то изменение высоты ![]() будет ничтожно мало, и можно сказать, что скорость изменения функции
будет ничтожно мало, и можно сказать, что скорость изменения функции ![]() фактически нулевая. В точках
фактически нулевая. В точках ![]() наблюдается именно такая картина.
наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: ![]() , то есть сделать его бесконечно малым.
, то есть сделать его бесконечно малым.
По итогу возникает ещё один закономерный вопрос: можно ли для дороги ![]() и её графика найти другую функцию, которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
и её графика найти другую функцию, которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.
Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
По аналогии с непрерывностью, «раскрутка» производной начинается с её изучения в отдельно взятой точке:
Производная функции в точке
Рассмотрим функцию ![]() (синий график), которая определена и непрерывна на некотором интервале, произвольную точку
(синий график), которая определена и непрерывна на некотором интервале, произвольную точку ![]() , принадлежащую данному интервалу, и соответствующее значение
, принадлежащую данному интервалу, и соответствующее значение ![]() :
:
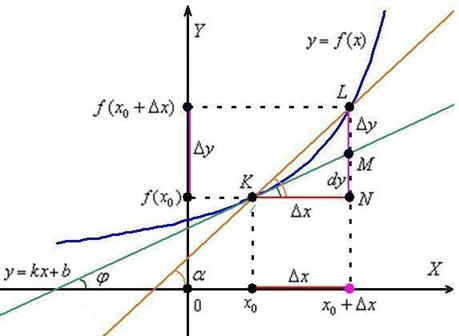
Зададим аргументу функции приращение ![]() (красный отрезок) в точке
(красный отрезок) в точке ![]() . Обратите внимание, что
. Обратите внимание, что ![]() – это тоже вполне определённая точка нашего интервала (на всякий случай отметил её малиновым цветом). И в этой точке существует своё значение функции
– это тоже вполне определённая точка нашего интервала (на всякий случай отметил её малиновым цветом). И в этой точке существует своё значение функции ![]() .
.
Приращение аргумента ![]() повлекло за собой приращение функции:
повлекло за собой приращение функции:
![]() (малиновый отрезок)
(малиновый отрезок)
В данном случае ![]() , поскольку в качестве примера выбран промежуток, на котором функция возрастает.
, поскольку в качестве примера выбран промежуток, на котором функция возрастает.
Давайте сразу возьмём на заметку, что нарисовалось в результате проделанных действий. Ну, конечно же, в глаза бросается секущая ![]() (коричневая прямая) и прямоугольный треугольник
(коричневая прямая) и прямоугольный треугольник ![]() .
.
Угол наклона секущей к оси ![]() я обозначил через
я обозначил через ![]() и отметил его коричневой дугой в двух местах. Такое внимание к данному углу не случайно – он однозначно определяется приращениями
и отметил его коричневой дугой в двух местах. Такое внимание к данному углу не случайно – он однозначно определяется приращениями ![]() . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник ![]() и угол
и угол ![]() . Согласно школьному определению, тангенс угла равен отношению противолежащего катета к прилежащему катету:
. Согласно школьному определению, тангенс угла равен отношению противолежащего катета к прилежащему катету: ![]()
Определение: производной функции в точке ![]() называется предел отношения приращения функции
называется предел отношения приращения функции ![]() к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента ![]() в этой точке при
в этой точке при ![]() . Или коротко:
. Или коротко:
![]()
Если данный предел конечен, то функция ![]() является дифференцируемой в точке
является дифференцируемой в точке ![]() . А то, что в львиной доле случаев предел
. А то, что в львиной доле случаев предел ![]() существует и конечен, скептики убедятся в самом ближайшем будущем.
существует и конечен, скептики убедятся в самом ближайшем будущем.
И, конечно же, не забываем о важнейшей особенности предела, как такового: ПРИНЦИПИАЛЬНЫЙ МОМЕНТ состоит в том, что приращение аргумента стремится к нулю, но нуля не достигает, иными словами, величина ![]() бесконечно малА, но не равна нулю!
бесконечно малА, но не равна нулю!
Геометрический смысл производной
Пожалуйста, возьмите в руки обычную линейку и совместите её ребро с прямой ![]() .
.
Да-да – приложите прямо к экрану монитора, не комплексуйте =) Вместо линейки можно использовать тетрадку, лист бумаги или даже руку.
Теперь, согласно определению производной ![]() , медленно двигаем линейку влево к точке
, медленно двигаем линейку влево к точке ![]() , уменьшая тем самым приращение
, уменьшая тем самым приращение ![]() . При этом приращение функции
. При этом приращение функции ![]() тоже уменьшается: точка
тоже уменьшается: точка ![]() будет бесконечно близко приближаться к точке
будет бесконечно близко приближаться к точке ![]() по горизонтали (красному отрезку), и точка
по горизонтали (красному отрезку), и точка ![]() – бесконечно близко приближаться к той же точке
– бесконечно близко приближаться к той же точке ![]() , но уже по графику функции
, но уже по графику функции ![]() (синей линии).
(синей линии).
В результате секущая ![]() стремится занять положение касательной
стремится занять положение касательной ![]() к графику функции
к графику функции ![]() в точке
в точке ![]() . Искомая касательная изображена зелёным цветом.
. Искомая касательная изображена зелёным цветом.
Таким образом, мы получили строгое определение касательной к графику функции:
Касательная к графику функции в точке – это предельное положение секущей в данной точке.
Вот что матан животворящий делает =)
Развиваем мысль дальше. Вспомним полученную ранее формулу тангенса угла наклона секущей ![]() и осуществим в обеих её частях так называемый предельный переход.
и осуществим в обеих её частях так называемый предельный переход.
В свете рассматриваемых событий (бесконечного уменьшения ![]() и нахождения предела
и нахождения предела ![]() ) угол наклона
) угол наклона ![]() секущей
секущей ![]() стремится к углу наклона
стремится к углу наклона ![]() касательной
касательной ![]() (последний дважды отмечен зелёными дугами). Аналогичное утверждение справедливо и для тангенсов данных углов:
(последний дважды отмечен зелёными дугами). Аналогичное утверждение справедливо и для тангенсов данных углов: ![]() . В итоге:
. В итоге:
![]()
Вывод: производная функции в точке ![]() численно равна тангенсу угла наклона касательной к графику функции в данной точке:
численно равна тангенсу угла наклона касательной к графику функции в данной точке: ![]() .
.
А тангенс угла наклона касательной – это в точности её угловой коэффициент:
![]()
В курсе аналитической геометрии выведена формула, по которой можно составить уравнение прямой с угловым коэффициентом:
![]()
Учитывая полученное равенство ![]() , перепишем уравнение в виде
, перепишем уравнение в виде ![]() .
.
Данной формулой мы уже активно пользовались, когда находили уравнение касательной, и сейчас стало ясно, откуда она взялась.
Существование производной в точке и непрерывность функции
По определению: ![]() , следовательно, существование производной в точке
, следовательно, существование производной в точке ![]() тесно связано с существованием предела
тесно связано с существованием предела ![]() в данной точке.
в данной точке.
Я изо всех сил пытался отсрочить этот момент, чтобы не путать посетителей сайта, но рассказать всё равно придётся…. В определении производной ВАЖНЕЙШИМ является тот факт, что приращение аргумента ![]() задаётся и в другую сторону. Возьмите карандаш и листок бумаги (не ленимся – так будет в 10 раз понятнее!!!!). Изобразите координатные оси, примерно такой же график функции
задаётся и в другую сторону. Возьмите карандаш и листок бумаги (не ленимся – так будет в 10 раз понятнее!!!!). Изобразите координатные оси, примерно такой же график функции ![]() и точки
и точки ![]() .
.
Отложите на чертеже небольшой отрезок ![]() слева от точки
слева от точки ![]() . При этом точка
. При этом точка ![]() расположится левее точки
расположится левее точки ![]() , а точка
, а точка ![]() – ниже точки
– ниже точки ![]() . Теперь проведите секущую графика функции
. Теперь проведите секущую графика функции ![]() и начните мысленно уменьшать приращение
и начните мысленно уменьшать приращение ![]() вправо к точке
вправо к точке ![]() . В результате данная секущая будет стремиться занять положение той же самой «зелёной» касательной!
. В результате данная секущая будет стремиться занять положение той же самой «зелёной» касательной!
Примечание: приращение с левой стороны осуществляется «против оси абсцисс» и поэтому отрицательно: ![]() . Заметьте, что всё остаётся корректным, так, в нашем случае соответствующее приращение
. Заметьте, что всё остаётся корректным, так, в нашем случае соответствующее приращение ![]() тоже меньше нуля, и по этой причине левосторонний предел таки будет положительным
тоже меньше нуля, и по этой причине левосторонний предел таки будет положительным ![]() , корректно показывая (как и его правосторонний коллега) рост функции в точке
, корректно показывая (как и его правосторонний коллега) рост функции в точке ![]() . Односторонние пределы конечны и совпадают, что говорит о существовании общего предела, производной и единой касательной.
. Односторонние пределы конечны и совпадают, что говорит о существовании общего предела, производной и единой касательной.
Таким образом, существование производной в точке геометрически очень удобно ассоциировать с существованием ОБЩЕЙ КАСАТЕЛЬНОЙ в данной точке.
Очевидно, что функция не дифференцируема в точках разрыва. Во-первых, она может быть не определена в такой точке, следовательно, приращение ![]() задать невозможно (на нет и суда нет). А во-вторых, практически всегда попросту не существует общего предела
задать невозможно (на нет и суда нет). А во-вторых, практически всегда попросту не существует общего предела ![]() (по причине различных «нехорошестей» с односторонними пределами). Читатели, насмотревшиеся графиков разрывных функций (это намёк ;-) = )), легко представят проблему с общей касательной.
(по причине различных «нехорошестей» с односторонними пределами). Читатели, насмотревшиеся графиков разрывных функций (это намёк ;-) = )), легко представят проблему с общей касательной.
Вывод: из дифференцируемости функции в точке ![]() необходимо (обязательно) следует её непрерывность в данной точке.
необходимо (обязательно) следует её непрерывность в данной точке.
Однако обратное утверждение в общем случае неверно, то есть из непрерывности функции дифференцируемость следует далеко не всегда! Классический пример, функция ![]() в точке
в точке ![]() (чертёж есть в Примере 24 урока о геометрических преобразованиях графика). Если рассмотреть приращение
(чертёж есть в Примере 24 урока о геометрических преобразованиях графика). Если рассмотреть приращение ![]() справа, то правосторонний предел будет равен
справа, то правосторонний предел будет равен ![]() , и, соответственно, получаем касательную
, и, соответственно, получаем касательную ![]() , совпадающую с правой частью графика
, совпадающую с правой частью графика ![]() . Если же придать приращение аргументу
. Если же придать приращение аргументу ![]() влево, получается совсем другой результат:
влево, получается совсем другой результат: ![]() и другая касательная
и другая касательная ![]() , которая совпадает с левой частью графика
, которая совпадает с левой частью графика ![]() . Печалька. Ни общего предела, ни общей касательной. Таким образом, функция
. Печалька. Ни общего предела, ни общей касательной. Таким образом, функция ![]() хоть и непрерывна в точке
хоть и непрерывна в точке ![]() , но не дифференцируема в ней! Подробное аналитическое доказательство проводится по шаблону Примера 11 статьи Производная по определению. Ещё один типичный образец есть в Примере 6 урока Непрерывность функции, где кусочно-заданная функция непрерывна на
, но не дифференцируема в ней! Подробное аналитическое доказательство проводится по шаблону Примера 11 статьи Производная по определению. Ещё один типичный образец есть в Примере 6 урока Непрерывность функции, где кусочно-заданная функция непрерывна на ![]() . Однако не всё так безоблачно – она не дифференцируема в точках «стыка» графика.
. Однако не всё так безоблачно – она не дифференцируема в точках «стыка» графика.
В заключение параграфа немного об особых случаях.
Когда предел ![]() равен «плюс» или «минус бесконечности», то производная тоже существует и касательная к графику функции будет параллельная оси
равен «плюс» или «минус бесконечности», то производная тоже существует и касательная к графику функции будет параллельная оси ![]() . Например, касательной к графику функции
. Например, касательной к графику функции ![]() (см. чертёж Примера 6 урока Методы решения определённых интегралов) в точке
(см. чертёж Примера 6 урока Методы решения определённых интегралов) в точке ![]() является сама ось ординат. Более того, если односторонние пределы бесконечны и различны по знаку, то единая касательная и производная всё равно существуют! Пожалуйста: квадратный корень из модуля «икс» в той же точке
является сама ось ординат. Более того, если односторонние пределы бесконечны и различны по знаку, то единая касательная и производная всё равно существуют! Пожалуйста: квадратный корень из модуля «икс» в той же точке ![]() .
.
За более детальной и подробной информацией по сабжу можно обратиться, например, к первому тому Фихтенгольца. НедУрно издание 1962 года, закачивается без проблем.
Раз пошла такая пьянка...:
Дифференциал функции в точке и его геометрический смысл
Дифференциалом функции ![]() в точке
в точке ![]() называют главную линейную часть приращения функции
называют главную линейную часть приращения функции ![]() (строго говоря, его следовало обозначить
(строго говоря, его следовало обозначить ![]() или
или ![]() ). На чертеже дифференциал
). На чертеже дифференциал ![]() в точке
в точке ![]() равен длине отрезка
равен длине отрезка ![]() .
.
Давайте снова возьмём в руки линейку и приложим её ребром к монитору на прямую ![]() . Двигая линейку влево к точке
. Двигая линейку влево к точке ![]() , уменьшаем приращение
, уменьшаем приращение ![]() . Впрочем, и сам выполню несколько засечек:
. Впрочем, и сам выполню несколько засечек:
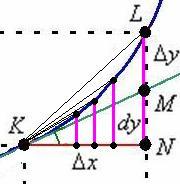
По рисунку хорошо видно, что с уменьшением ![]() уменьшается и приращение функции
уменьшается и приращение функции ![]() (малиновые линии). При этом отрезок
(малиновые линии). При этом отрезок ![]() занимает всё меньшую и меньшую часть приращения функции
занимает всё меньшую и меньшую часть приращения функции ![]() , а наш дифференциал
, а наш дифференциал ![]() – всю бОльшую и бОльшую его часть, именно поэтому его и называют главной частью приращения функции. Настолько главной, что при бесконечно малом
– всю бОльшую и бОльшую его часть, именно поэтому его и называют главной частью приращения функции. Настолько главной, что при бесконечно малом ![]() дифференциал стремится к полному приращению функции:
дифференциал стремится к полному приращению функции: ![]() (соответственно отрезок
(соответственно отрезок ![]() будет бесконечно малым).
будет бесконечно малым).
Нетрудно вывести формулу для приближенных вычислений с помощью дифференциала. Рассмотрим прямоугольный треугольник ![]() и тангенс угла наклона касательной
и тангенс угла наклона касательной ![]() . Обозначив дифференциал в рассматриваемой точке
. Обозначив дифференциал в рассматриваемой точке ![]() корректнее через
корректнее через ![]() , и учитывая, что
, и учитывая, что ![]() , получаем:
, получаем:
![]()
То есть идея формулы приближенных вычислений ![]() состоит в том, чтобы точное значение
состоит в том, чтобы точное значение ![]() функции (смотрим на ось ординат основного чертёжа) заменить суммой
функции (смотрим на ось ординат основного чертёжа) заменить суммой ![]() и отрезка
и отрезка ![]() . К слову, отрезок
. К слову, отрезок ![]() на главном чертеже существенно «не достаёт» до полного приращения
на главном чертеже существенно «не достаёт» до полного приращения ![]() , и это не случайность. В демонстрационной иллюстрации я выбрал большое значении
, и это не случайность. В демонстрационной иллюстрации я выбрал большое значении ![]() , чтобы всё было видно. На практике же, чем приращение
, чтобы всё было видно. На практике же, чем приращение ![]() меньше – тем дифференциал лучше «дотянется» до полного приращения функции (см. маленький рисунок), и тем точнее сработает формула
меньше – тем дифференциал лучше «дотянется» до полного приращения функции (см. маленький рисунок), и тем точнее сработает формула ![]() .
.
Провернём ещё один неожиданный фокус с полученным равенством ![]() . Предельно малое значение
. Предельно малое значение ![]() часто обозначают через
часто обозначают через ![]() , поэтому формула принимает вид
, поэтому формула принимает вид ![]() . Скинем
. Скинем ![]() в знаменатель противоположной части:
в знаменатель противоположной части:
![]()
Понятие производной функции
До сих пор речь шла о производной и дифференциале в единственной «подопытной» точке ![]() . Но ведь в качестве
. Но ведь в качестве ![]() можно взять ЛЮБУЮ ТОЧКУ
можно взять ЛЮБУЮ ТОЧКУ ![]() рассматриваемого интервала!
рассматриваемого интервала!
Из этих соображений в равенстве ![]() проведём замену
проведём замену ![]() и получим
и получим ![]() . А это не что иное, как обозначение производной
. А это не что иное, как обозначение производной ![]() , о котором я упомянул на первом же уроке по технике дифференцирования. Символ
, о котором я упомянул на первом же уроке по технике дифференцирования. Символ ![]() используется двояко – и как цельный символ производной, и как частное дифференциалов. Вторая интерпретация активно эксплуатируется в ходе решения дифференциальных уравнений.
используется двояко – и как цельный символ производной, и как частное дифференциалов. Вторая интерпретация активно эксплуатируется в ходе решения дифференциальных уравнений.
Естественно, и в самом определении производной в точке ![]() заменим
заменим ![]() на
на ![]() :
:
![]()
К чему мы пришли? А пришли мы к тому, что для функции ![]() по закону
по закону ![]() ставится в соответствие другая функция
ставится в соответствие другая функция ![]() , которая называется производной функцией (или просто производной).
, которая называется производной функцией (или просто производной).
Производная ![]() характеризует скорость изменения функции
характеризует скорость изменения функции ![]() . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку
. Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку ![]() области определения функции
области определения функции ![]() . Пусть функция дифференцируема в данной точке. Тогда:
. Пусть функция дифференцируема в данной точке. Тогда:
1) Если ![]() , то функция
, то функция ![]() возрастает в точке
возрастает в точке ![]() . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку
. И, очевидно, существует интервал (пусть даже очень малый), содержащий точку ![]() , на котором функция
, на котором функция ![]() растёт, и её график идёт «снизу вверх».
растёт, и её график идёт «снизу вверх».
2) Если ![]() , то функция
, то функция ![]() убывает в точке
убывает в точке ![]() . И существует интервал, содержащий точку
. И существует интервал, содержащий точку ![]() , на котором функция
, на котором функция ![]() убывает (график идёт «сверху вниз»).
убывает (график идёт «сверху вниз»).
3) Если ![]() , то бесконечно близко около точки
, то бесконечно близко около точки ![]() функция
функция ![]() сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции, в частности в точках минимума и максимума.
сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции, в частности в точках минимума и максимума.
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию ![]() , мы «выделяем» скорость её изменения в виде производной функции
, мы «выделяем» скорость её изменения в виде производной функции ![]() . А что, кстати, понимается под словом «производная»? Функция
. А что, кстати, понимается под словом «производная»? Функция ![]() произошла от функции
произошла от функции ![]() .
.
Термины весьма удачно истолковывает механический смысл производной:
Рассмотрим закон изменения координаты тела ![]() , зависящий от времени
, зависящий от времени ![]() , и функцию скорости движения данного тела
, и функцию скорости движения данного тела ![]() . Функция
. Функция ![]() характеризует скорость изменения координаты тела, поэтому является первой производной функции
характеризует скорость изменения координаты тела, поэтому является первой производной функции ![]() по времени:
по времени: ![]() . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
. Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного понятия «скорость тела».
Ускорение тела ![]() – это скорость изменения скорости, поэтому:
– это скорость изменения скорости, поэтому: ![]() . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
. Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
Откуда взялись правила дифференцирования и таблица производных? Невероятно, но все они появились благодаря единственной формуле: ![]() . И как это происходит, мы начнём разбирать прямо сейчас.
. И как это происходит, мы начнём разбирать прямо сейчас.
Действительно, пора переходить к практическим примерам. Ну а это был, пожалуй, первый обстоятельный теоретический материал, который я опубликовал на сайте – вполне можете взять для реферата или курсовика. Только аккуратнее, здесь есть зашифрованное послание для вашего преподавателя =)
Пример 1
Используя определение производной, доказать, что производная константы равна нулю.
Функция-константа имеет вид ![]() , и графически – это семейство прямых, параллельных оси абсцисс. Наверное, многие уже догадались, почему
, и графически – это семейство прямых, параллельных оси абсцисс. Наверное, многие уже догадались, почему ![]() .
.
Изобразим, например, график функции ![]() :
:
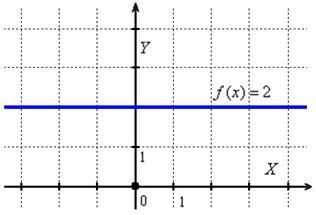
Это «ровная дорога», то есть функция и не возрастает и не убывает в каждой точке. Ни вверх и не вниз.
Покажем аналитически, что производная функции-константы равна нулю. Рассмотрим произвольное значение ![]() , в котором, понятно,
, в котором, понятно, ![]() . Придадим аргументу приращение:
. Придадим аргументу приращение: ![]() . Функция всё время постоянна, поэтому
. Функция всё время постоянна, поэтому ![]() и приращение функции:
и приращение функции: ![]() . По определению производной в точке:
. По определению производной в точке:
![]()
Заметьте, тут нет неопределённости: ноль, делённый на бесконечно малое число ![]() , равен нулю. Пытливые читатели могут взять в руки калькулятор и убедиться в этом.
, равен нулю. Пытливые читатели могут взять в руки калькулятор и убедиться в этом.
Поскольку в качестве точки ![]() можно взять любое «икс», то проведём замену
можно взять любое «икс», то проведём замену ![]() и получим:
и получим: ![]() .
.
Пример 2
Найти производную функции ![]() по определению.
по определению.
Рассмотрим произвольное значение ![]() , в котором
, в котором ![]() .
.
Зададим аргументу приращение ![]() и вычислим соответствующее значение функции:
и вычислим соответствующее значение функции: ![]() (обычная алгебра – в функцию
(обычная алгебра – в функцию ![]() вместо «икса» подставили
вместо «икса» подставили ![]() и раскрыли скобки).
и раскрыли скобки).
Вычислим приращение функции:
![]()
По определению производной в точке:
![]()
Поскольку в качестве ![]() можно взять любое значение
можно взять любое значение ![]() , то
, то ![]() .
.
О чём нам говорит найденная производная? Во-первых, для любого «икс» она отрицательна, а значит, функция ![]() убывает на всей области определения. И, во-вторых, это убывание постоянно, то есть «наклон горки везде одинаков» – в какой бы точке мы ни находились, предельное отношение
убывает на всей области определения. И, во-вторых, это убывание постоянно, то есть «наклон горки везде одинаков» – в какой бы точке мы ни находились, предельное отношение ![]() будет неизменным:
будет неизменным:
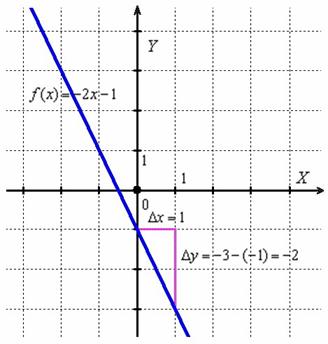
Здесь и далее я предполагаю, что читатель умеет находить, как минимум, простые производные, пользуясь правилами дифференцирования и таблицей. Давайте найдём производную «быстрым» способом: ![]()
Теперь вам должно быть понятно происхождение и весь неформальный смысл полученного результата.
Используя этот же алгоритм, можно решить задачу в общем виде и доказать, что производная линейной функции ![]() равна её угловому коэффициенту:
равна её угловому коэффициенту:
![]() .
.
В начале статьи Уравнение прямой на плоскости я проанализировал расположение прямой в зависимости от углового коэффициента. И сейчас получено объяснение данных фактов с точки зрения математического анализа. Действительно, рассмотрим две линейные функции ![]() и найдём их производные:
и найдём их производные:
![]()
Обе производные положительны, а значит, функции возрастают на всей области определения (графики идут «снизу вверх»). Кроме того, не забываем, что производная – это мера скорости изменения функции. Поскольку ![]() , то функция
, то функция ![]() растёт быстрее (причём, значительно) функции
растёт быстрее (причём, значительно) функции ![]() , и, соответственно, график
, и, соответственно, график ![]() намного более крут.
намного более крут.
Факт тривиален, но озвучу: касательная к графику линейной функции в каждой точке совпадает с самим графиком данной линейной функции.
Заключительная демонстрационная задача, думаю, развеет все оставшиеся непонятки:
Пример 3
Найти производную функции ![]() по определению.
по определению.
Рассмотрим произвольную точку ![]() и соответствующее значение
и соответствующее значение ![]() . Зададим приращение
. Зададим приращение ![]() и вычислим значение функции в точке
и вычислим значение функции в точке ![]() :
:
![]()
Найдём приращение функции:
![]()
По определению производной в точке:
![]()
Поскольку в качестве ![]() можно рассмотреть любую точку
можно рассмотреть любую точку ![]() области определения функции
области определения функции ![]() , то проведём замену
, то проведём замену ![]() и получим
и получим ![]() .
.
Проверим результат «лёгким» способом: ![]()
Исходная функция ![]() и её производная
и её производная ![]() – это две совершенно разные функции, однако между ними существует чёткая и прозрачная связь:
– это две совершенно разные функции, однако между ними существует чёткая и прозрачная связь:
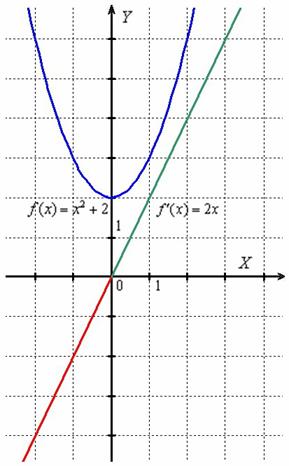
На интервале ![]() производная отрицательна:
производная отрицательна: ![]() (красная линия), что говорит об убывании функции
(красная линия), что говорит об убывании функции ![]() на данном интервале. Грубо говоря, ветвь параболы идёт сверху вниз. А на интервале
на данном интервале. Грубо говоря, ветвь параболы идёт сверху вниз. А на интервале ![]() производная положительна:
производная положительна: ![]() (зелёная линия), значит, функция
(зелёная линия), значит, функция ![]() растёт на этом интервале, и её график идёт снизу вверх.
растёт на этом интервале, и её график идёт снизу вверх.
При ![]() производная равна нулю:
производная равна нулю: ![]() . Найденное значение показывает, что скорость изменения функции
. Найденное значение показывает, что скорость изменения функции ![]() в точке
в точке ![]() равна нулю (функция не растёт в ней и не убывает). В данном случае здесь минимум функции.
равна нулю (функция не растёт в ней и не убывает). В данном случае здесь минимум функции.
Всё это можно утверждать даже не зная, что такое парабола и как выглядит график функции ![]() !
!
И ещё раз заостряю внимание, что значение производной в точке выражает собой некоторую меру скорости изменения функции в данной точке. Найдём несколько значений производной:
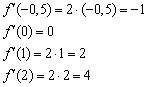
Таким образом, в точке ![]() функция
функция ![]() убывает, в точке
убывает, в точке ![]() сохраняет скорость постоянной, а в точках
сохраняет скорость постоянной, а в точках ![]() – растёт. Причём
– растёт. Причём ![]() , поэтому можно сказать (опять даже не зная чертежа!), что в окрестности точки
, поэтому можно сказать (опять даже не зная чертежа!), что в окрестности точки ![]() график функции
график функции ![]() идёт вверх круче, чем вблизи точки
идёт вверх круче, чем вблизи точки ![]() .
.
Закрепим геометрический смысл: производная в точке численно равна тангенсу угла наклона касательной к графику функции в данной точке. Не поленюсь, применю формулу ![]() четыре раза:
четыре раза:
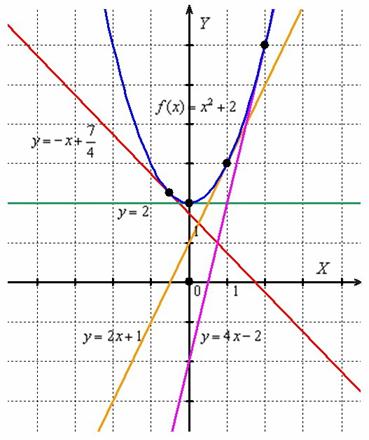
Вот так вот изящно производная характеризует свою функцию.
Наше увлекательное путешествие подошло к концу, и возникает вопрос: в каком направлении двигаться дальше? Это зависит от ваших сегодняшних потребностей:
– Можно потренироваться в нахождении производной по определению. И смех, и грех, но для применения формулы ![]() опять же совсем не обязательно понимать, что это производная =)
опять же совсем не обязательно понимать, что это производная =)
– Можно отработать и окончательно уяснить геометрический смысл производной на уроке Уравнения касательной и нормали.
– И, наконец, можно перейти в следующий раздел – к статье об экстремумах функции, из-за которой на сайте, собственно, и появилась теория.
Желаю успехов!
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта
