


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Абсолютная и условная сходимость несобственного интеграла.
Признак Дирихле. Признак Абеля
В предыдущих статьях мы исследовали сходимость интегралов 1-го и 2-го рода (см. по ссылкам), и в заключительной части урока рассмотрим важное понятие сходимости, которое касается и тех, и других «пациентов». Прежде всего, тех, у которых подынтегральная функция меняет знак.
Начнём по порядку, с интеграла 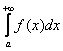 . Если функция
. Если функция ![]() положительна (неотрицательна), то проблем никаких – исследуем интеграл по обычной схеме. Если отрицательна – тоже, картинка отобразится симметрично относительно оси
положительна (неотрицательна), то проблем никаких – исследуем интеграл по обычной схеме. Если отрицательна – тоже, картинка отобразится симметрично относительно оси ![]() вниз, и ситуация будет зеркальной. Если
вниз, и ситуация будет зеркальной. Если ![]() где-то отрицательна, а затем положительна (или наоборот), то интеграл можно разделить на 2 части, и рассмотреть каждый кусок отдельно.
где-то отрицательна, а затем положительна (или наоборот), то интеграл можно разделить на 2 части, и рассмотреть каждый кусок отдельно.
Но как исследовать, например, с интеграл ![]() ? Здесь подынтегральная функция принимает то положительные, то отрицательные, то положительные, то отрицательные значения – и так далее, до бесконечности (все помнят синусоиду?). Такие функции называют знакопеременными. Что делать в этом случае?
? Здесь подынтегральная функция принимает то положительные, то отрицательные, то положительные, то отрицательные значения – и так далее, до бесконечности (все помнят синусоиду?). Такие функции называют знакопеременными. Что делать в этом случае?
Этому и посвящен сегодняшний разговор.
Рассмотрим интеграл  – с модулем, который уничтожает возможные отрицательные значения подынтегральной функции. Если данный интеграл сходится, то сходиться будет и интеграл
– с модулем, который уничтожает возможные отрицательные значения подынтегральной функции. Если данный интеграл сходится, то сходиться будет и интеграл  , при этом последний называют абсолютно сходящимся.
, при этом последний называют абсолютно сходящимся.
Примечание: откуда сразу следует, что сходящиеся интегралы от неотрицательных функций, например, 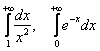 , сходятся абсолютно.
, сходятся абсолютно.
Пример 18
Исследовать интегралы на абсолютную сходимость
а) 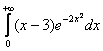 б)
б) ![]()
Решение:
а) На интервале от 0 до 3 подынтегральная функция отрицательна, а при бОльших значениях «икс» – положительна. При ином условии, данный интеграл можно разделить на 2 части:
 , и поскольку 1-й кусок сходится (т.к. это определённый интеграл), то всё дело сведётся к тривиальному исследованию.
, и поскольку 1-й кусок сходится (т.к. это определённый интеграл), то всё дело сведётся к тривиальному исследованию.
Но условие требует исследовать абсолютную сходимость, и поэтому нам следует рассмотреть интеграл:
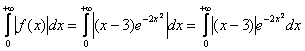 – помним, что экспонента положительна, а посему под модулем ей делать нечего.
– помним, что экспонента положительна, а посему под модулем ей делать нечего.
И сейчас я расскажу вам ещё об одном приёме сравнения, который можно использовать и в других примерах. Разложим экспоненту на множители, распишу очень подробно:
![]() – это преобразование можно выполнить при любом показателе
– это преобразование можно выполнить при любом показателе ![]() , и, признаться,
, и, признаться, ![]() я выбрал специально – чисто для удобства.
я выбрал специально – чисто для удобства.
Функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() и
и ![]() , следовательно, она ограничена на нём, то есть, существует число
, следовательно, она ограничена на нём, то есть, существует число ![]() , такое, что для всех
, такое, что для всех ![]() справедливо неравенство:
справедливо неравенство:
![]()
Таким образом:
![]() , значит, по признаку сравнения, интеграл
, значит, по признаку сравнения, интеграл 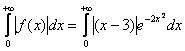 сходится вместе с интегралом
сходится вместе с интегралом 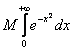 , сходимость которого мы установили в 1-й части урока (см. по ссылке выше).
, сходимость которого мы установили в 1-й части урока (см. по ссылке выше).
А из сходимости и  следует сходимость
следует сходимость 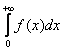 , таким образом, интеграл
, таким образом, интеграл  сходится, причём сходится абсолютно.
сходится, причём сходится абсолютно.
б) ![]() , ну, тут всё проще пареной репы.
, ну, тут всё проще пареной репы.
Рассмотрим интеграл: ![]()
Поскольку синус ограничен: ![]() , то
, то ![]() и для всех
и для всех ![]() из промежутка интегрирования справедливо неравенство:
из промежутка интегрирования справедливо неравенство:
![]() , значит, по признаку сравнения, интеграл
, значит, по признаку сравнения, интеграл ![]() сходится вместе с «эталонным» интегралом
сходится вместе с «эталонным» интегралом ![]() .
.
Вывод: интеграл ![]() сходится абсолютно.
сходится абсолютно.
Самостоятельно:
Пример 19
Исследовать абсолютную сходимость интеграла
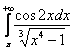
Решение в конце урока.
Но, как вы догадываетесь, это ещё не всё. А что, если интеграл 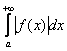 расходится? В этом случае интеграл
расходится? В этом случае интеграл 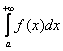 может не только расходиться, но и сходиться!
может не только расходиться, но и сходиться!
Если интеграл  сходится, но
сходится, но  расходится, то говорят, что он сходится условно.
расходится, то говорят, что он сходится условно.
Пример 20
Исследовать сходимость интеграла
![]()
Решение: при рассмотрении ![]() простых путей не видно, и поэтому мы переходим к прямому исследованию предложенного интеграла.
простых путей не видно, и поэтому мы переходим к прямому исследованию предложенного интеграла.
Немного забегая вперёд, скажу, что здесь удобно применить признак Дирихле, но почему бы не вооружиться на все случаи жизни?
![]()
Как и в случае с определённым интегралом, несобственный интеграл можно проинтегрировать по частям: 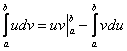 , единственное, у нас
, единственное, у нас ![]() , и вместо
, и вместо ![]() следует рассмотреть предел
следует рассмотреть предел ![]() .
.
Итак:
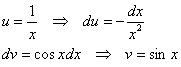
и по формуле:
![]()
Первое слагаемое равно конечному числу: 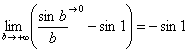 (предел бесконечно малой функции на ограниченную равен нулю - теорема есть такая (см. Пример 9)); второе слагаемое – это недавно разобранный абсолютно сходящийся интеграл.
(предел бесконечно малой функции на ограниченную равен нулю - теорема есть такая (см. Пример 9)); второе слагаемое – это недавно разобранный абсолютно сходящийся интеграл.
Таким образом, интеграл ![]() сходится. Осталось выяснить, условно или абсолютно.
сходится. Осталось выяснить, условно или абсолютно.
Исследуем сходимость интеграла
![]()
По «общим очертаниям» он напоминает расходящийся интеграл ![]() , и поэтому мы постараемся соорудить нужное неравенство, чтобы использовать признак сравнения. Для всех «икс» справедливо неравенство
, и поэтому мы постараемся соорудить нужное неравенство, чтобы использовать признак сравнения. Для всех «икс» справедливо неравенство ![]() – это понятно? – если значение из интервала
– это понятно? – если значение из интервала![]() возвести в квадрат, то получится мЕньшее значение. Таким образом, на промежутке интегрирования:
возвести в квадрат, то получится мЕньшее значение. Таким образом, на промежутке интегрирования:
![]()
Используя тригонометрическую формулу ![]() , получаем:
, получаем:
![]()
Интеграл ![]() – расходится, а интеграл
– расходится, а интеграл ![]() сходится – это «старший брат» нашего интеграла
сходится – это «старший брат» нашего интеграла ![]() , сходимость которого доказана в 1-й части задания. Следовательно, интеграл
, сходимость которого доказана в 1-й части задания. Следовательно, интеграл ![]() является расходящимся, и по признаку сравнения, интеграл
является расходящимся, и по признаку сравнения, интеграл ![]() тоже расходится.
тоже расходится.
Вывод: интеграл ![]() сходится условно.
сходится условно.
И теперь обещанный инструмент исследования:
Признак Дирихле: интеграл вида  сходится, если:
сходится, если:
1) функция ![]() интегрируема в любом конечном промежутке
интегрируема в любом конечном промежутке ![]() , где
, где ![]() и её первообразная
и её первообразная 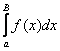 на этом промежутке ограничена;
на этом промежутке ограничена;
2) при ![]() функция
функция ![]() монотонно стремится к нулю:
монотонно стремится к нулю: ![]() .
.
Применим этот признак для только что разобранного интеграла ![]() , в котором обозначим:
, в котором обозначим: ![]() .
.
1) На промежутке ![]() функция
функция ![]() интегрируема:
интегрируема:
![]() – и для любого значения
– и для любого значения ![]() полученная первообразная ограничена, «на грубую», можно сделать оценку:
полученная первообразная ограничена, «на грубую», можно сделать оценку: ![]() .
.
2) При ![]() функция
функция ![]() монотонно убывает до нуля:
монотонно убывает до нуля: ![]() (графически это обычная «школьная» гипербола).
(графически это обычная «школьная» гипербола).
Таким образом, интеграл ![]() сходится по признаку Дирихле.
сходится по признаку Дирихле.
Следует отметить, что требование монотонности функции ![]() – существенно, и если оно не выполнено, то признак Дирихле не срабатывает, т.е. интеграл может, как сходиться, так и расходиться. Может быть не всем понятен термин – на всякий случай нарисую пример немонотонного убывания:
– существенно, и если оно не выполнено, то признак Дирихле не срабатывает, т.е. интеграл может, как сходиться, так и расходиться. Может быть не всем понятен термин – на всякий случай нарисую пример немонотонного убывания:

Такая вот совсем не монотонная картинка с весёлыми подпрыгиваниями :) …что это за функция? ![]()
С помощью признака Дирихле легко установить, что интегралы вида ![]() сходятся при любом
сходятся при любом ![]() , т.к. монотонность функций
, т.к. монотонность функций ![]() совершенно очевидна – все они по форме похожи на гиперболу
совершенно очевидна – все они по форме похожи на гиперболу ![]() .
.
Но, как вы, наверное, поняли, признак Дирихле не даёт ответа на вопрос, сходится ли интеграл 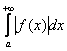 . Это достаточный признак сходимости интеграла
. Это достаточный признак сходимости интеграла 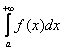 .
.
Следствием признака Дирихле является достаточный признак Абеля:
интеграл вида  сходится, если:
сходится, если:
1) интеграл 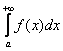 сходится (не важно, условно или абсолютно);
сходится (не важно, условно или абсолютно);
2) функция ![]() монотонна и ограничена на
монотонна и ограничена на ![]() .
.
Здесь сразу приходит на ум такой пример:
![]()
1) интеграл ![]() сходится, 2) на промежутке интегрирования арктангенс монотонно возрастает и ограничен:
сходится, 2) на промежутке интегрирования арктангенс монотонно возрастает и ограничен: ![]() , значит, по признаку Абеля, данный интеграл сходится.
, значит, по признаку Абеля, данный интеграл сходится.
Следующие интегралы для самостоятельного решения:
Пример 21
Исследовать сходимость интегралов
а) ![]() , б)
, б) ![]()
В пункте «а» следует провести замену ![]() и перейти к новым пределам интегрирования (так, как мы это сделали в Примере 17), далее исследуем полученный интеграл – в плане сходимости он будет эквивалентен исходному.
и перейти к новым пределам интегрирования (так, как мы это сделали в Примере 17), далее исследуем полученный интеграл – в плане сходимости он будет эквивалентен исходному.
Решение и ответы в конце урока.
Хочу обратить внимание, что формулировка «исследовать сходимость» обычно подразумевает то, что сначала нужно исследовать сходимость предложенного интеграла, и только потом (если потребуется) – сходимость интеграла с модулем. В случае с «халявными» интегралами, наподобие ![]() , преподаватель может запросто вернуть задание на доработку, если вы исследовали только интеграл
, преподаватель может запросто вернуть задание на доработку, если вы исследовали только интеграл ![]() .
.
И в заключение статьи рассмотрим условную и абсолютную сходимость несобственных интегралов 2-го рода.
Она определяется аналогично. Пусть подынтегральная функция терпит бесконечный разрыва слева или справа, тогда интеграл 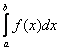 называют абсолютно сходящимся, если сходится
называют абсолютно сходящимся, если сходится 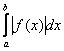 , и условно сходящимся, если он сходится, но
, и условно сходящимся, если он сходится, но  – расходится.
– расходится.
Пример 22
Исследовать сходимость интеграла

Решение: подынтегральная функция терпит бесконечный разрыв слева и является знакопеременной. Исследуем сходимость интеграла:

Поскольку ![]() , то для всех значений промежутка интегрирования справедливо неравенство:
, то для всех значений промежутка интегрирования справедливо неравенство:
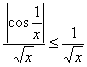 , значит, по признаку сравнения, интеграл
, значит, по признаку сравнения, интеграл  сходится вместе с «эталонным» интегралом
сходится вместе с «эталонным» интегралом ![]() , откуда следует и сходимость интеграла
, откуда следует и сходимость интеграла  .
.
Вывод: исследуемый интеграл сходится абсолютно.
Но то был «лёгкий» путь, в котором мы не исследовали сам интеграл  . И возникает вопрос: как его исследовать напрямую?
. И возникает вопрос: как его исследовать напрямую?
С помощью аналогичного признака Дирихле, сформулирую его как раз для разрыва слева:
Интеграл вида  сходится, если:
сходится, если:
1) функция ![]() интегрируема в любом конечном промежутке
интегрируема в любом конечном промежутке ![]() , где
, где ![]() и её первообразная
и её первообразная ![]() на этом промежутке ограничена;
на этом промежутке ограничена;
2) при ![]() функция
функция ![]() монотонно стремится к нулю:
монотонно стремится к нулю: ![]() .
.
Представим наш интеграл в виде 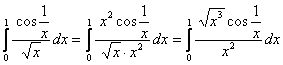 и обозначим
и обозначим 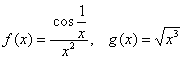
1) Функция ![]() интегрируема в любом конечном промежутке
интегрируема в любом конечном промежутке ![]() , где
, где ![]() :
:
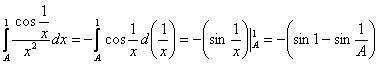 – и более того, её первообразная ограничена в этом промежутке (в силу естественной ограниченности синуса).
– и более того, её первообразная ограничена в этом промежутке (в силу естественной ограниченности синуса).
2) При ![]() функция
функция ![]() монотонно убывает до нуля:
монотонно убывает до нуля: ![]() .
.
Вывод: интеграл  сходится по признаку Дирихле. Ну а абсолютную сходимость мы установили ранее.
сходится по признаку Дирихле. Ну а абсолютную сходимость мы установили ранее.
И, разумеется, для интегралов 2-го рода справедлив признак Абеля (формулирую снова для точки разрыва слева):
Интеграл вида  сходится, если:
сходится, если:
1) интеграл  сходится (условно или абсолютно);
сходится (условно или абсолютно);
2) функция ![]() монотонна и ограничена на
монотонна и ограничена на ![]() .
.
Посмотрим, как это работает на практике:
Пример 23
Исследовать сходимость интеграла
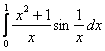
Решение: здесь мы пойдём академичным путём и начнём с прямого исследования предложенного интеграла, в котором обозначим  и используем признак Абеля:
и используем признак Абеля:
1) Исследуем сходимость интеграла  . Для этого проведём замену
. Для этого проведём замену ![]() , и тогда
, и тогда  – если есть какие-то сомнения, выполните обратную замену
– если есть какие-то сомнения, выполните обратную замену ![]() .
.
Выясним, во что превратится дифференциал:
так как ![]() , то
, то ![]()
И осталось найти новые пределы интегрирования:
– если ![]() , то
, то ![]() ;
;
– если ![]() , то
, то ![]()
Вот такая вот метаморфоза! В результате замены несобственный интеграл сменил свой род:
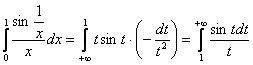 – полученный интеграл сходится условно (см. Пример 20 и после), а значит, таковым является и исходный интеграл
– полученный интеграл сходится условно (см. Пример 20 и после), а значит, таковым является и исходный интеграл 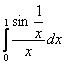 .
.
2) Со вторым пунктом признака Абеля всё проще: на полуинтервале ![]() функция
функция ![]() ограничена:
ограничена: ![]() и при
и при ![]() монотонно убывает до единицы:
монотонно убывает до единицы: ![]() . Геометрически – это кусок всем известной параболы.
. Геометрически – это кусок всем известной параболы.
Вывод: интеграл  сходится по признаку Абеля.
сходится по признаку Абеля.
Исследуем его на абсолютную сходимость:

И здесь снова удобно заменить переменную: ![]() , тогда:
, тогда:
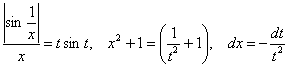 , и новые пределы интегрирования уже найдены выше:
, и новые пределы интегрирования уже найдены выше:
 – первый интеграл сходится по признаку сравнения
– первый интеграл сходится по признаку сравнения 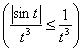 , а вот второй расходится, но уже по другой части того же признака:
, а вот второй расходится, но уже по другой части того же признака: ![]() (тоже знакомый мотив из Примеров 20, 21).
(тоже знакомый мотив из Примеров 20, 21).
Таким образом, интеграл 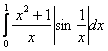 расходится, а значит, интеграл
расходится, а значит, интеграл 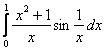 сходится условно.
сходится условно.
Готово!
Но на практике такая жесть, конечно, встречается крайне редко (это надо как-то очень углублённо учиться :)), и поэтому чисто символический интеграл для самостоятельного решения:
Пример 24
Исследовать сходимость интеграла
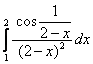
На этом цикл статей, посвящённых исследованию несобственных интегралов, завершён – желаю успехов и до скорых встреч!
Решения и ответы:
Пример 19. Решение:  .
.
Поскольку ![]() , то:
, то:
![]()
Исследуем сходимость интеграла 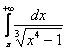 . Сравним его со сходящимся интегралом
. Сравним его со сходящимся интегралом ![]() («эталонный» интеграл). Используем предельный признак сравнения:
(«эталонный» интеграл). Используем предельный признак сравнения:
 – конечное число, отличное от нуля, значит, интеграл
– конечное число, отличное от нуля, значит, интеграл 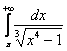 сходится вместе с интегралом
сходится вместе с интегралом ![]() , и в силу установленного выше неравенства (по «обычному» признаку сравнения), сходится и интеграл
, и в силу установленного выше неравенства (по «обычному» признаку сравнения), сходится и интеграл  .
.
Таким образом, интеграл  сходится абсолютно.
сходится абсолютно.
Пример 21. Решение:
а) ![]()
Проведём замену: ![]() . Согласно проведенной замене,
. Согласно проведенной замене, ![]() и и новые пределы интегрирования:
и и новые пределы интегрирования:
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]() .
.
![]()
Обозначим ![]()
1) На промежутке ![]() функция
функция ![]() интегрируема:
интегрируема:
![]() – и для любого значения
– и для любого значения ![]() полученная первообразная ограничена.
полученная первообразная ограничена.
2) при ![]() функция
функция ![]() монотонно убывает до нуля:
монотонно убывает до нуля: ![]() .
.
Таким образом, интеграл ![]() сходится по признаку Дирихле.
сходится по признаку Дирихле.
Исследуем его на абсолютную сходимость:
![]()
На всех значений ![]() справедливо неравенство
справедливо неравенство ![]() , поэтому:
, поэтому:
![]()
Используем тригонометрическую формулу ![]() :
:
![]()
Интеграл ![]() расходится, а интеграл
расходится, а интеграл ![]() сходится по признаку Дирихле, значит, интеграл
сходится по признаку Дирихле, значит, интеграл ![]() расходится, и по признаку сравнения, вместе с ним расходится и интеграл
расходится, и по признаку сравнения, вместе с ним расходится и интеграл ![]() .
.
Вывод: интеграл ![]() сходится условно, и в силу проведённой замены, условно сходится и интеграл
сходится условно, и в силу проведённой замены, условно сходится и интеграл ![]() .
.
б) В интеграле ![]() обозначим
обозначим ![]() .
.
1) Интеграл ![]() сходится по признаку Дирихле.
сходится по признаку Дирихле.
2) На промежутке интегрирования экспонента ограничена: ![]() и монотонно убывает от
и монотонно убывает от ![]() до нуля:
до нуля: ![]() .
.
Таким образом, исследуемый интеграл сходится по признаку Абеля.
И другой способ решения, на который указал один из читателей: можно обозначить ![]() и использовать признак Дирихле. Но это если вам хорошо понятно, почему функция
и использовать признак Дирихле. Но это если вам хорошо понятно, почему функция ![]() убывает монотонно.
убывает монотонно.
Исследуем интеграл на абсолютную сходимость:

Так как ![]() , то:
, то:
![]()
На промежутке интегрирования ![]() , поэтому:
, поэтому:
![]() , таким образом, по признаку сравнения (по построенной цепочке неравенства), интеграл
, таким образом, по признаку сравнения (по построенной цепочке неравенства), интеграл 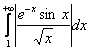 сходится вместе с интегралом
сходится вместе с интегралом ![]() .
.
Вывод: исследуемый интеграл сходится абсолютно.
Пример 24. Решение: проведём прямое вычисление:
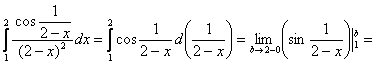
![]() – данного предела не существует, а значит, не существует и предложенного несобственного интеграла.
– данного предела не существует, а значит, не существует и предложенного несобственного интеграла.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright