Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

18. Эмпирический коэффициент детерминации
и эмпирическое корреляционное отношение.
Поле корреляции и эмпирические линии регрессии

Об эмпирическом коэффициенте детерминации я уже рассказал на уроке о дисперсиях (конец Примера 59), а об эмпирическом корреляционном отношении – после выполнения аналитической группировки (Пример 61). Более того, мы вычислили эти показатели в ходе выполнения указанных задач. И если вы до сих пор с ними не ознакомились, то пройдите по ссылкам. «Чайникам» рекомендую начать со статьи Группировка данных.

Сейчас нам встретятся те же самые показатели, только рассчитываться они будут немного по-другому – в рамках комбинационной группировки. И мы, конечно, повторим их суть. Для опытных читателей оглавление:

– эмпирический коэффициент детерминации;
– эмпирическое корреляционное отношение;
– корреляционная зависимость и причинно-следственная связь (читать всем!);
– корреляционное поле и эмпирическая линия регрессии,

и обо всём по порядку, как обычно, в конкретной задаче:

Пример 65

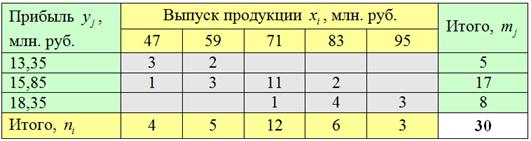
Имеются выборочные данные о выпуске продукции и сумме прибыли по 30 предприятиям:

Внимание! Эту таблицу мы построили на уроке Комбинационная группировка (Пример 63), и если вам не очень понятно её устройство, то ОБЯЗАТЕЛЬНО разберитесь. Без этого дальше никуда.

Теперь задание:

1) Вычислить эмпирический коэффициент детерминации и эмпирическое корреляционное отношение. Сделать выводы.

2) Построить корреляционное поле и эмпирическую линию регрессии. Прокомментировать полученный график.

Решение: анализируя комбинационную таблицу, легко заметить, что частоты в серых ячейках имеют тенденцию располагаться по диагонали от левого верхнего к правому нижнему углу. Это говорит о наличии прямой корреляционной зависимости прибыли предприятий  от выпуска продукции  – чем больше выпускают предприятия, тем в среднем больше их прибыль.

Однако на размер прибыли, очевидно, влияет не только этот, но и множество других факторов, в том числе случайных. И возникает вопрос: как оценить весомость фактора, положенного в основу комбинационной группировки? Иными словами, насколько жИво или вяло «откликается» прибыль на изменение выпуска продукции?

Ответ на этот вопрос даёт:

1) Эмпирический коэффициент детерминации:

 – есть отношение межгрупповой дисперсии к общей дисперсии.

Общая дисперсия  учитывает ВСЕ причины, которые влияют на вариацию признака-результата (прибыли). Межгрупповая дисперсия  учитывает влияние фактора, положенного в основу группировки (выпуска продукции).

Эмпирический коэффициент детерминации характеризует ДОЛЮ влияния группировочного фактора (выпуска продукции). Данный коэффициент изменяется в пределах , и чем он ближе к единице, тем сильнее влияние группировочного фактора на признак-результат (прибыль).

Дело за малым – вычислить  и .

В «шапке» и в левом столбце комбинационной таблицы (см. выше) у нас находятся два интервальных вариационных ряда и сначала нужно перейти к дискретным рядам, выбрав в качестве вариант  и  середины соответствующих интервалов:

На всякий случай примеры расчёта: .

Вычислим общую среднюю признака-результата:
 млн. руб.

и общую дисперсию:

Разбираемся с межгрупповой дисперсией. Для её нахождения вычислим групповые или, как их называют, условные средние. При условии  средняя прибыль составит:
 млн. руб.
и давайте ещё в качестве закрепляющего примера приведу расчёт для :
 млн. руб.

Промежуточные вычисления удобно заносить рядышком, наращивая комбинационную таблицу:

Полагаю, после моих видео вам не составит труда автоматизировать эти вычисления в Экселе. Вычислим межгрупповую дисперсию:

В качестве факультативного задания предлагаю самостоятельно вычислить групповые дисперсии ( по каждой из пяти групп), внутригрупповую дисперсию и проверить правило сложения дисперсий . Я выполнил это в обязательном порядке, дабы избежать ошибок.

Вычислим эмпирический коэффициент детерминации:
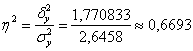 – таким образом, 66,93% вариации прибыли обусловлено изменением  выпуска продукции. Остальные 33,07% вариации обусловлены другими факторами.

Исходя из правило сложения дисперсий , легко понять, что за остальную вариацию отвечает внутригрупповая дисперсия , графически она характеризует меру разброса частот в серых столбцах (см. таблицу выше).

Теперь повторим суть коэффициента детерминации. Чем ближе  к единице, тем больше межгрупповая дисперсия  и меньше . Высокое значение  говорит о том, что групповые средние  знАчимо отличаются от общей средней , то есть изменение значений «икс» приводит к существенному изменению значений «игрек». Иными словами, признак-фактор действительно оказывает сильное влияние. При этом внутригрупповая  дисперсия  будет малА и частоты в серой области примут выраженный диагональный вид. В предельном случае   (и нулевом значении ) речь идёт о строгой функциональной зависимости.

Обратно, малые значения  обусловлены тем, что межгрупповая дисперсия  близкА к нулю – по той причине, что групповые средние  близкИ к общей средней . Это означает, что на изменение значений «икс» – «игреки» «откликаются» слабо. При этом внутригрупповая дисперсия  будет большой – это значит, что дисперсия в группах существенна и частоты в серых столбцах более разбросаны – фактически они заполнят всю серую область и, естественно, утратят диагональный вид.

Кто всё понял, тот монстр :)

Следующий показатель:

эмпирическое корреляционное отношение

– есть квадратный корень из эмпирического коэффициента детерминации:

Данный показатель тоже изменяется в пределах   и характеризует тесноту (силу) корреляционной зависимости. Чем ближе  к единице, тем сильнее зависит признак-результат  от признака-фактора  – тем «жёстче» реагируют значения «игрек» на изменение значений «икс». И наоборот, чем ближе  к нулю, тем зависимость слабее – тем более вяло реагируют «игреки» на изменение значений «икс».

Для качественной оценки этой силы используют уже известную вам шкалу Чеддока, скопирую её из статьи Аналитическая группировка:

Следует заметить, что эта шкала не единственна, в разных источниках информации вы можете встретить немного разные градации.

В нашей задаче:
 – таким образом, существует сильная корреляционная зависимость прибыли предприятия  от выпуска продукции .

И ещё раз подчёркиваю, что это всего лишь одна из математических моделей, а не какая-то «абсолютная» истина. Так, в Примере 61, работая с теми же исходными данными, мы получили  и . Но, несмотря на то, что та и эта модель несколько разные – результаты по содержательному смыслу получились примерно одинаковыми. Вообще говоря, первая модель (Пример 61) более точная, но зато вторая (с комбинационной группировкой) более компактная и информативная, что становится актуальным при увеличении объёма выборки.

Да, а почему показатели называют эмпирическими? Потому что они получены опытным путём. Ещё их можно назвать эмпирическими выборочными коэффициентами. И если мы возьмём другую случайную репрезентативную выборку предприятий, то получим другие значения  (в рамках и той и другой модели). Однако они вряд ли будут сильно отличаться от уже полученных результатов.

Теперь поговорим о недостатках эмпирического коэффициента детерминации и эмпирического корреляционного отношения. Начнём с главного и, пожалуй, фундаментального момента, который удостоился отдельного параграфа:

Корреляционная зависимость и причинно-следственная связь

Это разные вещи.

Если между признаками  существует сильная корреляционная зависимость, то это ещё не значит, что между ними есть взаимосвязь. Так, если мы возьмём два произвольных вариационных ряда, которые примерно одинаково растут (или убывают), то в любом случае получатся высокие значения . При этом между признаками может вообще не быть никакой причинно-следственной связи, а-ля  – сезонное размножение сусликов в Монголии и  – скорость свободного падения кирпича с Пизанской башни.

Поэтому причинно-следственная зависимость признака  от  должна быть предварительно обоснована если не экспертным путём, то хотя бы здравым смыслом. Как это произошло в примере с котами и в нашей задаче с выпуском продукции и прибылью. И уже выявленная в ходе решения корреляционная зависимость лишь подтверждает зависимость причинно-следственную.

С другой стороны, если коэффициенты  близки к нулю (слабая корреляционная зависимость), то это ещё не значит, что между признаками нет причинно-следственной связи. Представьте, что вы с разной силой дёргаете ручку игрового автомата, на котором крутятся бананчики, вишенки, семёрки и другие картинки. Есть ли причинно-следственная связь между вашими действиями и тем, что выпало на автомате? Безусловно. Но вот корреляционной зависимости (выпавших картинок от ваших усилий) нет никакой. Частоты в комбинационной таблице будут расположены хаотично, а при большом количестве испытаний примерно равномерно, и коэффициенты   устремятся к нулю. Таким образом, к некоторым (и даже многим) зависимостям вообще нельзя применять метод корреляционного анализа.  Или же можно, но работать он будет плохо.

Основная предпосылка использования корреляционного анализа состоит в том, что при изменении одного фактора – другой должен гипотетически (по нашему предположению и обоснованию) возрастать или убывать.

Кроме того, величина  может зависеть от  косвенно, опосредованно, и удачный тому пример есть в Википедии: очевидно, что между уличным травматизмом и количеством ДТП существует выраженная корреляционная зависимость, однако, эти показатели прямо не зависят друг от друга, у них есть общая причина – погодные условия (гололед, туман и т.д.).

Ещё раз перечитайте и хорошо ОСМЫСЛИТЕ вышесказанное!

Какие ещё есть недостатки у коэффициентов ?

– Данные коэффициенты не отражают направление корреляционной зависимости. Так, если вам просто покажут значение , то невозможно сказать, обратная здесь зависимость или прямая. В простейшем случае этот факт определяется логическим путём либо визуально – смотрим, как расположены частоты в комбинационной таблице, и делаем соответствующий вывод. Да, и графики, графики ещё есть! – на которых хорошо виднА корреляционная зависимость, читаем о следующем недостатке:

– Эмпирические коэффициенты ничего нам не говорят о форме зависимости. Под формой имеется в виду функция, которой можно удачно приблизить эмпирические (точечные) значения показателей, и график этой функции. И здесь мы плавно подошли к заключительному пункту задачи, который открывает ещё одну большую тему:

2) Корреляционное поле и эмпирическая линия регрессии

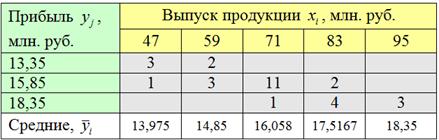
Корреляционное поле – это множество точек с абсциссами  и ординатами , которые соответствуют ненулевым значениям частот .

Для осмысления определения я просто скопирую сверху комбинационную таблицу:

и приведу готовое корреляционное поле:

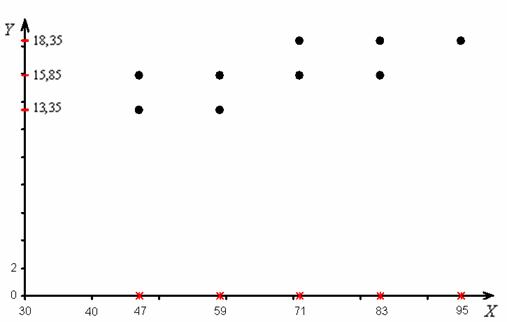
При этом сами частоты  (числа в серых ячейках) на графике никак не отмечаются. И уже по внешнему виду корреляционного поля можно сказать, что зависимость здесь прямая («чем больше, тем больше»). О том, как выполнить такой симпатичный чертёж, смотрите здесь, правда, ролик относится уже к следующим урокам

Далее. Что такое регрессия?

В статистическом смысле регрессия – это зависимость средних значений  признака-результата от соответствующих значений  признака-фактора.

Термин «регрессия» появился исторически, и желающие могут найти эту историю в Сети. Если быть лаконичным, то полученные средние значения «игрек» регрессивно возвращают нас к первопричине – соответствующим исходным значениям «икс».

Эмпирическая линия регрессии   к  (именно так) – это ломаная, соединяющая точки :

В Экселе не составляет никакого труда добавить ломаную, отсылаю вас к тому же видео. Построенная ломаная проходит максимально близко к точкам корреляционного поля, при этом учитываются весомость частот , на основе которых были вычислены значения  (см. начало 1-го пункта задачи).

Эмпирическая линия регрессии используется не только для наглядного изображения корреляционной зависимости, но и для интерполяции промежуточных значений…, сейчас объясню :) Рассматривая различные промежуточные значения выпуска продукции (промежуточные «иксы», отличные от ) мы можем достаточно точно оценить соответствующие средние значения прибыли («игреки средние»).

Задание выполнено.

Но тема продолжается. Дело в том, что существует два «комплекта» коэффициентов  и две линии регрессии. Это обусловлено тем, что встречаются ситуации, где признаки  взаимно влияют друг на друга. Приведу философский пример, адаптированный к современным реалиям:)

 – количество произведённых куриц на птицефабрике;
 – количество произведённых яиц.

Совершенно понятно, что здесь как признак  влияет на , так и наоборот. И мы можем вычислить два «комплекта» показателей. Первый комплект – как в только что рассмотренной задаче:
 – коэффициенты, которые показывают степень зависимости  от . Графическое изображение зависимости – эмпирическая линия регрессии   к – есть ломаная, соединяющая точки .

И второй комплект:
 – коэффициенты, характеризующие  зависимость  от . Эмпирическая линия регрессии   к  – есть ломаная, соединяющая точки .

Для расчёта коэффициентов второго комплекта используют «зеркальные» формулы, и желающие могут исследовать этот вопрос самостоятельно. Если честно, не припомню, чтобы в студенческих работах требовалось находить коэффициенты . Но вот изобразить вторую линию регрессии – требовалось, и в качестве демонстрации я построю её для данных только что прорешанной задачи. Для наглядности снова скопирую табличку сверху:

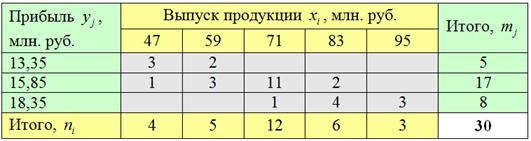
Вычислим «икс среднее» по каждой из трёх групп.  При :
;
при :
;
и при :
.

Изобразим на чертеже то же корреляционное поле (оно у нас одно) и эмпирическую линию регрессии  к   – ломаную, соединяющую точки :

Готово. Звенья ломаной расположились почти по прямой, и это наводит на светлую мысль: а нельзя ли приблизить эмпирические точки линейной функцией? Во многих случаях это будет удачным решением! А, главное, технически простым. Об этом речь пойдёт на следующих уроках – о линейном коэффициенте корреляции и уравнении линейной регрессии.

Ну а пока закрепим материал, и я, конечно же, не мог не вернуться к этой задаче:

Пример 66

По результатам выборочного исследования 100 котов получены следующие данные:

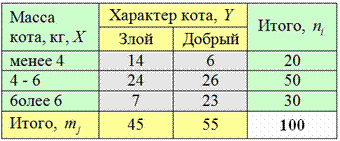
Требуется исследовать корреляционную зависимость доброты кота от его массы:

1) Вычислить эмпирический коэффициент детерминации и эмпирическое корреляционное отношение. Сделать выводы.

2) Построить корреляционное поле и эмпирическую линию регрессии.

Указание: при переходе к дискретному ряду взять значения 3,5 кг, 5 и 7 кг. Злых котов обозначить «минус» единицей, а добрых – «плюс» единицей.

Также обратите внимание, что здесь признак-фактор расположен слева по вертикали, а признак-результат – в «шапке» таблицы. Как я уже отмечал, именно такое расположение чаще всего встречается в практических задачах. Но тем лучше – тем лучше вы осмыслите формулы и алгоритм решения.

Образец для сверки рядом, и мы, наконец, переходим к «попсовой» теме, которая встречается повсеместно, даже у закоренелых гуманитариев  – Линейный коэффициент корреляции по курсу.

Решения и ответы:

Пример 66. Решение: перейдём к дискретным рядам распределения:

1) Эмпирический коэффициент детерминации найдем по формуле:

Вычислим общую среднюю:
 – средняя доброта кота в выборке.
Вычислим общую дисперсию:

Вычислим групповые средние. У тощих котов  средняя доброта составляет:
,
у обычных котов :

и у толстых котов :
.
Вычислим межгрупповую дисперсию:

Эмпирический коэффициент детерминации:
 – таким образом, 10,92% вариации доброты котов обусловлено их массой, остальные 89,06% вариации обусловлено другими причинами. Таки условия жизни и воспитание кота имеют куда бОльшее значение :)

Вычислим эмпирическое корреляционное отношение:
 – таким образом, существует слабо-умеренная корреляционная зависимость доброты кота от его массы.

Примечание: о достаточно низком значении этих показателей нам говорили частоты  комбинационной таблицы, которые не имели ярко выраженного диагонального вида.

2) Построим корреляционное поле и эмпирическую линию регрессии – ломаную, соединяющую точки :

З.Ы. Это, конечно, была задача-шутка :) Но если у кого-то есть реальное исследование на данную тему – пишите!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте