


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Линейные преобразования для «чайников»
На двух ближайших уроках я вкратце расскажу вам ещё об одном разделе высшей алгебры, который касается линейных преобразований… и тут сразу, заметьте, напрашивается добавить «преобразований чего-то». Тема обширная, тема интересная, и моя скромная задача состоит в том, чтобы в доступной форме донести до читателя её основы. В этой связи статья будет посвящена не только абстрактным алгебраическим вопросам, но и наполнена богатым геометрическим содержанием. Кроме того, сегодня мы обобщим такое важное понятие как вектор, имеющий к сему содержанию лишь частное отношение.
Есть ли среди вас начинающие изучать высшую математику? …хотя, чего тут спрашивать, конечно же, есть… – не смогли ведь пройти мимо заголовка! …Ну вот вы мне и попались, голубчики =) Для эффективного изучения материала нужно знать основы алгебры, аналитической геометрии, а также уметь выполнять действия с матрицами. На самом деле всё довольно просто, но если у вас возникнут вопросы (или уже встретился какой-то непонятный термин), то, пожалуйста, воспользуйтесь ссылками.
Обобщение понятия вектора. Векторное пространство
Ожидание казни хуже самой казни и поэтому лучше сразу почувствовать леденящий холодок настоящей алгебры =) Начнём с обещанного разбора полётов, а именно с понятия вектора. Давайте вспомним, что мы о нём знаем. Палочка со стрелочкой, знакомая ещё из школы. В высшей математике эта палочка «поднялась» до свободного вектора плоскости и пространства. Хорошо…. Далее слово «вектор» встретилось нам в ходе изучения матриц. Так, например, матрицу «один на два» ![]() мы называем вектором-строкой, а матрицу «три на один»
мы называем вектором-строкой, а матрицу «три на один» ![]() – вектором-столбцом. Это векторы? Да, это векторы! Причём эти векторы сами по себе не имеют никакого отношения к геометрии. В своих статьях по алгебре я неоднократно оговаривался, что «данный вектор нужно понимать в алгебраическом смысле» и на уроке о ранге матрицы привёл краткую теоретическую справку по этому поводу: вектор
– вектором-столбцом. Это векторы? Да, это векторы! Причём эти векторы сами по себе не имеют никакого отношения к геометрии. В своих статьях по алгебре я неоднократно оговаривался, что «данный вектор нужно понимать в алгебраическом смысле» и на уроке о ранге матрицы привёл краткую теоретическую справку по этому поводу: вектор ![]() – это упорядоченный набор чисел
– это упорядоченный набор чисел ![]() (обычно действительных)… и далее по тексту. А вот это уже более близко к истине: здесь, скажем, двумерный вектор
(обычно действительных)… и далее по тексту. А вот это уже более близко к истине: здесь, скажем, двумерный вектор ![]() понимается именно как упорядоченная пара чисел, которую, в частности можно интерпретировать, как координаты геометрического вектора. Или как решение системы линейных уравнений (см., например, статью об однородных системах). Или ещё как-нибудь.
понимается именно как упорядоченная пара чисел, которую, в частности можно интерпретировать, как координаты геометрического вектора. Или как решение системы линейных уравнений (см., например, статью об однородных системах). Или ещё как-нибудь.
Но и это частность! На самом деле в определённом контексте векторами являются матрицы, многочлены, функции и т.д. …и даже наши «обычные» действительные числа! А почему нет? Пожалуйста: множество векторов ![]() (никаких геометрических ассоциаций!), имеющих в наборе одно действительное число
(никаких геометрических ассоциаций!), имеющих в наборе одно действительное число ![]() .
.
Так что же такое вектор? Что объединяет все эти случаи?
Предположим, что для всех элементов некоторого множества определены операции их сложения ![]() и умножения на скаляр
и умножения на скаляр ![]() , причём результаты этих операций (полученные элементы) тоже принадлежат данному множеству. Если при этом выполнены следующие восемь аксиом (см. по ссылке), то рассматриваемые элементы называются векторами (никаких ассоциаций!!), а всё их множество – векторным или линейным пространством
, причём результаты этих операций (полученные элементы) тоже принадлежат данному множеству. Если при этом выполнены следующие восемь аксиом (см. по ссылке), то рассматриваемые элементы называются векторами (никаких ассоциаций!!), а всё их множество – векторным или линейным пространством ![]()
Обратите внимание на обозначения: абстрактный вектор чаще всего записывают жирной буквой – чтобы не возникало путаницы с различными «конкретными» векторами. Для векторного пространства стандартно используется буква ![]() .
.
Итак, какие бы «частные семейства» векторов мы ни взяли (геометрические, матричные, строковые и т.д.) – для каждой из этих алгебраических структур справедливо следующее:
– все элементы рассматриваемого множества можно складывать и умножать на скаляр (далее работаем с действительными числами), причём результаты этих операций тоже принадлежат данному множеству.
– для операций сложения и умножения выполнены аксиомы векторного пространства.
И здесь следует отметить, что термины «сложение» и «умножение» тоже носят общий символический смысл – в зависимости от природы того или иного векторного пространства эти операции определяются по-разному.
В курсе линейной алгебры проводится скрупулезная проверка различных множеств на предмет того, образуют ли они линейное пространство. И если удастся определить сложение и умножение на скаляр медведей на велосипеде и доказать для данных операций выполнение указанных 8 аксиом, то векторами будут и эти объекты =)
А теперь к основной теме урока:
Что такое линейное преобразование?
Если в линейном пространстве ![]() каждому вектору
каждому вектору ![]() по некоторому правилу
по некоторому правилу ![]() поставлен в соответствие вектор
поставлен в соответствие вектор ![]() этого же пространства, то говорят, что в данном пространстве задана векторная функция векторного аргумента:
этого же пространства, то говорят, что в данном пространстве задана векторная функция векторного аргумента: ![]() (во избежание разночтений с другими математическими записями скобки нередко опускают:
(во избежание разночтений с другими математическими записями скобки нередко опускают: ![]() ).
).
Данная функция называется линейным преобразованием, если для неё выполнены пресловутые свойства линейности, с которыми вы ещё не раз столкнётесь в ходе изучения высшей математики:
![]() ,
,
![]() , где
, где ![]() – произвольные векторы данного пространства, а
– произвольные векторы данного пространства, а ![]() – действительное число.
– действительное число.
Линейное преобразование также называют линейным оператором.
Следующий пример оброс не только бородой, но и волосами на спине: рассмотрим линейное пространство векторов-строк вида ![]() , в котором определены операция сложения
, в котором определены операция сложения ![]() и умножения вектора на число
и умножения вектора на число ![]() .
.
Никакой геометрии!!! – то, что я сформулировал в статье о ранге матрицы, называется ![]() -мерным арифметическим векторным пространством, и сейчас мы имеем дело с частным арифметическим пространством размерности 2.
-мерным арифметическим векторным пространством, и сейчас мы имеем дело с частным арифметическим пространством размерности 2.
Докажем, что функция векторного аргумента ![]() является линейным преобразованием. Доказательство состоит в проверке свойств линейности:
является линейным преобразованием. Доказательство состоит в проверке свойств линейности:
![]()
Здесь мы воспользовались дистрибутивностью умножения на скаляр относительно сложения векторов (одна из аксиом векторного пространства)
![]()
А здесь – аксиомой ассоциативности умножения на скаляр, коммутативностью (перестановочностью) самих действительных чисел (аксиома поля) и снова той же аксиомой ассоциативности.
Читателям, которым предстоит изучать теорию высшей алгебры, следует привыкнуть к таким доказательствам. Беспощадно формально, но, как сказали бы древние римляне, Dura algebra sed algebra =)
Таким образом, ![]() – это линейное преобразование.
– это линейное преобразование.
Разумеется, далеко не всякий оператор является линейным, и в других источниках информации можно найти массу примеров, как на удачную, так и неудачную проверку различных преобразований ![]() на линейность. И со строгостью доказательств на практике обычно всё попроще, …хотя, тут от преподавателя зависит – и по-хорошему, в математике ещё нужно обосновать, почему «ноль не равен единице».
на линейность. И со строгостью доказательств на практике обычно всё попроще, …хотя, тут от преподавателя зависит – и по-хорошему, в математике ещё нужно обосновать, почему «ноль не равен единице».
Ну а сейчас мы спускаемся на землю грешную и переходим к геометрическому смыслу линейных преобразований. Пусть ![]() – это множество геометрических векторов плоскости. Для простоты рассмотрим привычный ортонормированный базис и прямоугольную систему координат
– это множество геометрических векторов плоскости. Для простоты рассмотрим привычный ортонормированный базис и прямоугольную систему координат ![]() .
.
Если задан какой-либо базис, то линейное преобразование удобнее представить в матричном виде. Как записать оператор в виде матрицы? На этот счёт существует общее правило: чтобы записать матрицу линейного преобразования в ![]() -мерном базисе
-мерном базисе ![]() нужно последовательно и строго по порядку применять данный оператор к базисным векторам, а результаты заносить в столбцы матрицы (слева направо).
нужно последовательно и строго по порядку применять данный оператор к базисным векторам, а результаты заносить в столбцы матрицы (слева направо).
Наш случай элементарен: сначала применим линейное преобразование ![]() к первому базисному вектору:
к первому базисному вектору: ![]() и запишем результат в 1-й столбец:
и запишем результат в 1-й столбец: ![]() . Затем «обрабатываем» 2-й орт:
. Затем «обрабатываем» 2-й орт: ![]() и заносим полученные координаты во 2-й столбец:
и заносим полученные координаты во 2-й столбец:
![]() – матрица линейного преобразования
– матрица линейного преобразования ![]() в базисе
в базисе ![]() .
.
Протестируем построенную матрицу с помощью вектора ![]() . Для этого «уложим» его координаты в вектор-столбец и выполним следующее матричное умножение:
. Для этого «уложим» его координаты в вектор-столбец и выполним следующее матричное умножение:
![]() – в результате «на выходе» получены координаты вектора
– в результате «на выходе» получены координаты вектора ![]() , что и требовалось проверить.
, что и требовалось проверить.
Поскольку любая точка плоскости ![]() однозначно определяется её радиус-вектором
однозначно определяется её радиус-вектором ![]() (
(![]() – начало координат), то матрица преобразования, по существу, применима и к координатам точек. И далее для простоты я буду говорить, что, например, точка
– начало координат), то матрица преобразования, по существу, применима и к координатам точек. И далее для простоты я буду говорить, что, например, точка ![]() :
:
![]() – перешла в точку
– перешла в точку ![]() .
.
Наверное, все уже поняли, что делает этот оператор. Мысленно представьте произвольный треугольник на плоскости. После применения рассматриваемого линейного преобразования данный треугольник увеличится в два раза. Такие треугольники (имеющие равные соответствующие углы), как многие помнят из школы, называются подобными. Да и сам оператор носит такое же название:
Линейное преобразование ![]() называется преобразованием подобия или гомотетией, причём:
называется преобразованием подобия или гомотетией, причём:
– если ![]() , то речь идёт об однородном растяжении (увеличении) объектов плоскости в
, то речь идёт об однородном растяжении (увеличении) объектов плоскости в ![]() раз;
раз;
– если ![]() – то о сжатии (уменьшении) в
– то о сжатии (уменьшении) в ![]() раз;
раз;
– если ![]() , то преобразование тождественно (ничего не меняет).
, то преобразование тождественно (ничего не меняет).
И если ![]() меньше нуля, то дополнительно к растяжению/сжатию/неизменности векторы меняют направление, а точки отображаются симметрично относительно начала координат.
меньше нуля, то дополнительно к растяжению/сжатию/неизменности векторы меняют направление, а точки отображаются симметрично относительно начала координат.
При ![]() имеет место так называемое нулевое преобразование.
имеет место так называемое нулевое преобразование.
Следует отметить, что на прикладном и «любительском» уровне линейные преобразования чаще всего как раз и ассоциируются именно с геометрическими преобразованиями. Рассмотрим ещё несколько популярных примеров по теме, и, чтобы разнообразить серые геометрические будни, мысленно нарисуем на координатной плоскости кошачью морду. Можно и не мысленно =)
…Представили? Нарисовали? Отлично!
Преобразование ![]() растягивает объекты плоскости по направлению вектора
растягивает объекты плоскости по направлению вектора ![]() (горизонтали) в 2 раза, после чего кот Леопольд радует нас своей широкой-широкой улыбкой!
(горизонтали) в 2 раза, после чего кот Леопольд радует нас своей широкой-широкой улыбкой!
…хотя у многих, наверное, не кот… да и не факт, что с улыбкой… – как говорится, у каждого в голове своя морда =)
И в самом деле, преобразуем точку ![]() :
:
![]() – «иксовая» координата увеличилась в 2 раза, а «игрековая» – не изменилась.
– «иксовая» координата увеличилась в 2 раза, а «игрековая» – не изменилась.
Преобразование ![]() сожмёт кота по горизонтали в 3 раза. Желающие могут по ходу объяснений
сожмёт кота по горизонтали в 3 раза. Желающие могут по ходу объяснений приготовить мясорубку тестировать для рассматриваемых матриц различные векторы и точки. Читателям с маломальскими навыками матричного умножения не составит особого труда делать это устно.
Преобразование ![]() вытянет все ненулевые объекты плоскости по направлению вектора
вытянет все ненулевые объекты плоскости по направлению вектора ![]() (по вертикали) в полтора раза. Это будет очень удивлённый кот....
(по вертикали) в полтора раза. Это будет очень удивлённый кот....
Дополнительные знаки «минус» приведут к зеркальному отображению объектов (относительно оси ординат либо начала координат).
![]() – образно говоря, «челюсть налево, лоб направо». Это преобразование называется перекосом или сдвигом плоскости в направлении вектора
– образно говоря, «челюсть налево, лоб направо». Это преобразование называется перекосом или сдвигом плоскости в направлении вектора ![]() (в данном случае).
(в данном случае).
![]() – данное преобразование поворачивает векторы системы
– данное преобразование поворачивает векторы системы ![]() против часовой стрелки на угол
против часовой стрелки на угол ![]() .
.
И, наконец, венчает все эти метаморфозы ещё один лохматый пример:
преобразование ![]() переводит единичный квадрат с вершинами
переводит единичный квадрат с вершинами ![]() в параллелограмм с вершинами
в параллелограмм с вершинами ![]() .
.
А тут уж дело случая – может получиться, как комната смеха, так и комната страха – зависит от того или иного преобразования.
Из вышесказанного нетрудно понять, что в базисе ![]() любой квадратной матрице «два на два» соответствует некоторое линейное преобразование, и наоборот любому линейному преобразованию соответствует своя матрица «два на два». И данный факт справедлив вообще для любого аффинного базиса
любой квадратной матрице «два на два» соответствует некоторое линейное преобразование, и наоборот любому линейному преобразованию соответствует своя матрица «два на два». И данный факт справедлив вообще для любого аффинного базиса ![]() , причём одно и то же линейное преобразование в разных базисах будет иметь в общем случае разные матрицы (что следует из самого принципа формирования этих матриц).
, причём одно и то же линейное преобразование в разных базисах будет иметь в общем случае разные матрицы (что следует из самого принципа формирования этих матриц).
По аналогичной схеме можно рассмотреть векторы ![]() нашего трёхмерного пространства, с тем отличием, что преобразований будет больше, преобразования будут веселее. И, разумеется, линейные преобразования «работают» в векторных пространствах бОльшей размерности, однако там они уже далеки от геометрии.
нашего трёхмерного пространства, с тем отличием, что преобразований будет больше, преобразования будут веселее. И, разумеется, линейные преобразования «работают» в векторных пространствах бОльшей размерности, однако там они уже далеки от геометрии.
Разминаемся:
Пример 1
В некотором аффинном базисе задано линейное преобразование ![]() . Найти образ точки
. Найти образ точки ![]() . Используя обратное преобразование, выполнить проверку.
. Используя обратное преобразование, выполнить проверку.
Решение: потихоньку нагружаю вас терминологией: образ – это то, что должно получиться в результате преобразования. В данном случае, очевидно, должна получиться некоторая точка ![]() . Исходная точка
. Исходная точка ![]() , соответственно, является прообразом.
, соответственно, является прообразом.
! Надеюсь, все понимают, что штрихи в данном контексте не имеют никакого отношения к производным.
Образы векторов и точек мы уже неоднократно находили выше:

Таким образом, линейное преобразование перевело точку ![]() в точку
в точку ![]() .
.
Теперь найдём матрицу обратного преобразования, которое превращает образы векторов и точек обратно в их прообразы. Для этого запишем простейшее матричное уравнение ![]() (где
(где ![]() – координатный столбец прообразов, а
– координатный столбец прообразов, а ![]() – образов) и для его разрешения относительно
– образов) и для его разрешения относительно ![]() умножим обе части на обратную матрицу
умножим обе части на обратную матрицу ![]() слева:
слева:

«Развернём» уравнение в привычном порядке:
![]()
Обратную матрицу можно найти через алгебраические дополнения либо методом Гаусса-Жордана, но здесь я рекомендую первый способ, поскольку он позволит быстро выяснить, а существует ли матрица ![]() вообще.
вообще.
Заряжаем стандартный алгоритм. Сначала вычислим определитель:
![]() , значит, матрица линейного преобразования обратима. С содержательной точки зрения это означает, что обратное линейное преобразование существует и задаётся оно в точности матрицей
, значит, матрица линейного преобразования обратима. С содержательной точки зрения это означает, что обратное линейное преобразование существует и задаётся оно в точности матрицей ![]() .
.
Здесь и далее я не буду подробно расписывать процесс нахождения обратной матрицы. Итак, в результате стандартных действий находим ![]() и выясняем, во что превратится найденная точка
и выясняем, во что превратится найденная точка ![]() :
:
 – получены координаты исходной точки
– получены координаты исходной точки ![]() , что и требовалось проверить.
, что и требовалось проверить.
Ответ: ![]()
Следует отметить, что обратное преобразование осуществимо далеко не всегда. Так бывает, например, при проектировании векторов на координатные оси или при тривиальном нулевом преобразовании. В таких случаях определитель матрицы прямого оператора равен нулю ![]() и обратной матрицы
и обратной матрицы ![]() не существует.
не существует.
Творческая задача для самостоятельного решения:
Пример 2
В результате применения оператора ![]() в некотором базисе получены образы
в некотором базисе получены образы ![]() . Найти прообразы данных векторов.
. Найти прообразы данных векторов.
Краткое решение и ответ в конце урока. Обратите внимание, что формулировка данной задачи вовсе не утверждает, что речь идёт именно о геометрических векторах. Как оно, собственно, и бывает в большинстве типовых заданий, которые для полного комфорта оформляются малопонятной клинописью:
Пример 3
Даны два линейных преобразования:

Спокойно, спокойно, сейчас во всём разберёмся…
Средствами матричного исчисления найти преобразование, выражающее ![]() через
через ![]() .
.
Решение: и как раз первое, что здесь можно сказать – это отсутствие информации о характере векторов  . Известно только, что они заданы в некотором базисе, ибо матрица линейного преобразования НЕ МОЖЕТ существовать без базиса (т.к. она порождается базисными векторами). Сам базис нам тоже не известен, но для решения задачи информация о нём и не нужна.
. Известно только, что они заданы в некотором базисе, ибо матрица линейного преобразования НЕ МОЖЕТ существовать без базиса (т.к. она порождается базисными векторами). Сам базис нам тоже не известен, но для решения задачи информация о нём и не нужна.
Тем не менее, для пущего понимания предположим, что все дела происходят в обычной декартовой системе координат ![]() . И, чтобы не прослыть живодёром, я рассмотрю 3D-модель кота Леопольда =)
. И, чтобы не прослыть живодёром, я рассмотрю 3D-модель кота Леопольда =)
Запишем матрицу левого преобразования:  . Данное преобразование переводит векторы
. Данное преобразование переводит векторы  в образы
в образы 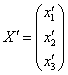 . Систему, кстати, удобнее переписать в виде уже знакомого матричного уравнения:
. Систему, кстати, удобнее переписать в виде уже знакомого матричного уравнения:
 или, если короче:
или, если короче: ![]() .
.
Данный оператор определённым образом преобразует все векторы (а значит и точки) пространства. Геометрически это означает, что кот Леопольд, оказывается, например, сплющенным (не знаю, не проверял).
Теперь ВНИМАТЕЛЬНО записываем матрицу второго преобразования: 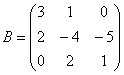 (здесь существует немалый риск поставить ноль не там где нужно). Данное преобразование переводит векторы
(здесь существует немалый риск поставить ноль не там где нужно). Данное преобразование переводит векторы  в образы
в образы 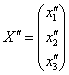 , в результате чего «сплющенный кот», скажем, растягивается вдоль какой-нибудь плоскости.
, в результате чего «сплющенный кот», скажем, растягивается вдоль какой-нибудь плоскости.
Аналогично – запишем преобразование в матричном виде:
 или:
или: ![]()
По условию, нужно найти результирующее (композиционное) преобразование, которое нам сразу даст «сплющенного и растянутого Леопольда». Подставим ![]() в уравнение
в уравнение ![]() :
:
![]()
Всё оказалось до безобразия просто – главное, матрицы перемножить в правильном порядке. Вычислим матрицу композиционного преобразования:

Если вы позабыли само матричное умножение, обратитесь к статье Свойства матричных операций, где я подробнейшим образом разобрал этот случай.
В результате:
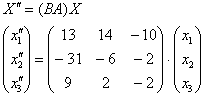
Осуществим матричное умножение в правой части:

Две матрицы равны, если равны их соответствующие элементы. Таким образом, итоговое преобразование, выражающее координаты векторов-образов ![]() через координаты векторов-прообразов
через координаты векторов-прообразов![]() , запишется в виде следующей системы:
, запишется в виде следующей системы:

Выполним проверку. Для этого подставим уравнения ![]() ,
, ![]() левой системы (см. условие) в правую часть каждого уравнения 2-й системы:
левой системы (см. условие) в правую часть каждого уравнения 2-й системы:
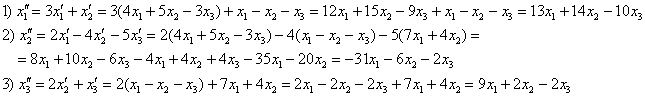
Что и требовалось проверить.
Этот способ, кстати, можно было бы рискнуть взять и за основной, если бы итоговое преобразование не требовалось найти средствами матричного исчисления
Ответ: 
Как пользоваться этой системой? Очень просто – берём например, вектор  и тупо подставляем его координаты:
и тупо подставляем его координаты:
 – таким образом, он превратился в вектор
– таким образом, он превратился в вектор  .
.
Более академичный способ – использование матричного уравнения ![]() .
.
Энтузиасты могут смоделировать деформацию кота Леопольда с помощью специализированного программного обеспечения и отправить мне картинку, которую я обязательно опубликую. Мне и самому интересно, что же там с ним на самом деле произошло =) И такой энтузиаст нашёлся! – Леопольд,… выходи в 3d 8^)! Он и в самом деле оказался довольно сильно «сплюснутым и растянутым». Модель реализована в среде Wolfram Mathematica, вот картинка с другого ракурса, и это, к слову, уже дополнительное линейное преобразование. Выражаю особую благодарность всем, кто присылает свои решения, на сайте есть немало творческих задач и предложений, порой, даже жестоких :)
В том случае, если нужно «вернуть кота к первоначальному виду», следует найти обратную матрицу результирующего преобразования ![]() и воспользоваться уравнением
и воспользоваться уравнением ![]() .
.
«Плоский» случай для самостоятельного решения:
Пример 4
Даны два линейных преобразования в некотором базисе:
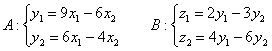
Найти образ вектора ![]() двумя способами:
двумя способами:
1) путём последовательного применения преобразований ![]() и
и ![]() ;
;
2) с помощью композиционного оператора, выражающего координаты ![]() через
через ![]() .
.
Был велик соблазн вас запутать, но всё же я воздержался. Однако на практике нужно иметь в виду следующее:
– системы запросто могут быть переставлены местами;
– условие задачи может требовать выразить ![]() через
через ![]() и тогда потребуется дополнительно находить обратную матрицу результирующего преобразования;
и тогда потребуется дополнительно находить обратную матрицу результирующего преобразования;
В этой связи очень важно РАЗОБРАТЬСЯ в сути задания, и если что-то осталось недопонятым, обязательно перечитайте объяснения ещё раз – не лишним будет даже порисовать.
А сейчас переходим к вопросу, который назревал в течение всего урока:
Матрица линейного преобразования в различных базисах
В начале статьи мы выяснили происхождение матрицы линейного преобразования на примере оператора ![]() и ортонормированного базиса
и ортонормированного базиса ![]() . Напоминаю: для того, чтобы записать матрицу линейного оператора в каком-либо базисе, нужно строго по порядку подействовать этим оператором на базисные векторы и полученные координаты занести в столбцы матрицы (слева направо). В результате «обработки» векторов
. Напоминаю: для того, чтобы записать матрицу линейного оператора в каком-либо базисе, нужно строго по порядку подействовать этим оператором на базисные векторы и полученные координаты занести в столбцы матрицы (слева направо). В результате «обработки» векторов ![]() нами была составлена матрица
нами была составлена матрица ![]() данного линейного преобразования в данном базисе.
данного линейного преобразования в данном базисе.
Но ведь на «школьном» базисе свет клином не сошёлся! Ничто нам не мешает перейти к произвольному базису ![]() , где это же линейное преобразование, скорее всего, выразится другой матрицей. Но сам-то оператор не изменится – он будет по-прежнему увеличивать векторы плоскости в 2 раза. Таким образом, справедливо следующее утверждение, которое по существу уже было озвучено ранее:
, где это же линейное преобразование, скорее всего, выразится другой матрицей. Но сам-то оператор не изменится – он будет по-прежнему увеличивать векторы плоскости в 2 раза. Таким образом, справедливо следующее утверждение, которое по существу уже было озвучено ранее:
одно и то же линейное преобразование в разных базисах в общем случае имеет РАЗНЫЕ матрицы.
И следующие две задачи как раз посвящены этому вопросу:
Пример 5
В базисе ![]() задано линейное преобразование
задано линейное преобразование ![]() . Найти матрицу данного преобразования в базисе
. Найти матрицу данного преобразования в базисе ![]() , если
, если 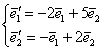
Решение: в условии задачи опять ничего не сказано о характере векторов, но для наглядности предположим, что данные базисы являются аффинными базисами плоскости. Как заметили внимательные читатели, предложенное линейное преобразование вытягивает все ненулевые объекты плоскости в направлении координатного вектора ![]() в 2 раза, и наша задача состоит в том, чтобы записать матрицу
в 2 раза, и наша задача состоит в том, чтобы записать матрицу ![]() этого же преобразования в новом базисе
этого же преобразования в новом базисе ![]() . Для решения этого вопроса существует специальная формула:
. Для решения этого вопроса существует специальная формула:
![]() , где
, где ![]() – матрица перехода от базиса
– матрица перехода от базиса ![]() к базису
к базису ![]() .
.
Составляется она просто: берём вектор ![]() и «укладываем» коэффициенты его разложения (внимание!) в 1-й столбец матрицы:
и «укладываем» коэффициенты его разложения (внимание!) в 1-й столбец матрицы: ![]() . Затем рассматриваем вектор
. Затем рассматриваем вектор ![]() и заносим коэффициенты его разложения во 2-й столбец:
и заносим коэффициенты его разложения во 2-й столбец:
![]()
Внимание! Базисные векторы, в данном случае векторы ![]() , следует «перебирать» строго по порядку!
, следует «перебирать» строго по порядку!
Остальное дело техники. Находим обратную матрицу:
![]()
Произведение:
![]()
И, наконец, матрицу рассматриваемого линейного преобразования в новом базисе:
![]()
Пользуясь ассоциативностью матричного умножения, можно было сначала найти ![]() , а затем
, а затем ![]() , но, в общем-то, это уже несущественные детали.
, но, в общем-то, это уже несущественные детали.
Ответ: ![]()
Ещё раз повторим смысл задания: само линейное преобразование не поменялось – оно по-прежнему растягивает ненулевые объекты плоскости вдоль «старого» вектора ![]() в 2 раза и не деформирует их в направлении вектора
в 2 раза и не деформирует их в направлении вектора ![]() , но в новом базисе
, но в новом базисе ![]() матрица данного преобразования уже другая. И вы видите её в ответе.
матрица данного преобразования уже другая. И вы видите её в ответе.
Очевидно, что найденная матрица ![]() задаёт обратное преобразование, т. е. выражает старые базисные векторы через новые. Аккуратно «транспонируем» столбцы матрицы в коэффициенты соответствующей системы:
задаёт обратное преобразование, т. е. выражает старые базисные векторы через новые. Аккуратно «транспонируем» столбцы матрицы в коэффициенты соответствующей системы: 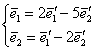 . Таким образом, при желании всегда можно вернуться к старому базису:
. Таким образом, при желании всегда можно вернуться к старому базису: ![]() . Обратная формула следует из простых логических соображений, но её можно вывести и формально – разрешив матричное уравнение
. Обратная формула следует из простых логических соображений, но её можно вывести и формально – разрешив матричное уравнение ![]() относительно
относительно ![]() .
.
Иногда матрицы ![]() и
и ![]() называют подобными.
называют подобными.
Какой базис удобнее? Ну конечно, исходный ![]() , где матрица преобразования имеет вид
, где матрица преобразования имеет вид ![]() , и сразу виднА характерная особенность этого преобразования. А что это за такой интересный базис, и как отыскать эту матрицу, вы узнаете на уроке о собственных векторах.
, и сразу виднА характерная особенность этого преобразования. А что это за такой интересный базис, и как отыскать эту матрицу, вы узнаете на уроке о собственных векторах.
Трехмерный случай для самостоятельного решения:
Пример 6
Найти матрицу линейного преобразования в базисе ![]() , где
, где ![]() ,
, ![]() ,
, ![]() , если она задана в базисе
, если она задана в базисе ![]() .
.

Пожалуйста, не путайте это задание с Примером № 3 – по первой оглядке здесь тоже какие-то похожие равенства, тоже штрихи, но смысл совершено другой. Если там шла речь о двух линейных преобразованиях и взаимосвязи координат векторов, то здесь – об одном и том же преобразовании и взаимосвязи векторов двух базисов.
Краткое решение и ответ совсем рядом.
И в завершении урока вернёмся к двумерному случаю и матрицам «два на два». Казалось бы, с геометрической точки зрения эти матрицы задают линейные преобразования плоскости и разговор закончен. Но на самом деле это не так – у матриц есть и другой геометрический смысл, с которым можно ознакомиться на уроке Переход к новому базису. Сначала я хотел включить пару соответствующих примеров в эту статью, но чуть позже решил, что материал будет уместнее опубликовать в разделе аналитической геометрии.
Ну и конечно, не забываем, что рассматриваемый материал касается не только геометрических векторов плоскости и пространства, но и вообще любых векторов.
Спасибо за внимание, жду вас на следующем, не менее увлекательном уроке о собственных числах и собственных векторах линейного преобразования.
Решения и ответы:
Пример 2 Решение: найдём матрицу обратного преобразования:
![]() (см. урок. Как найти обратную матрицу)
(см. урок. Как найти обратную матрицу)
Найдём прообразы:
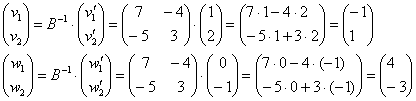
Ответ: ![]()
Пример 4. Решение: запишем матрицы преобразований:
![]()
1) Последовательно применим к вектору ![]() преобразования
преобразования ![]() и
и ![]() :
:
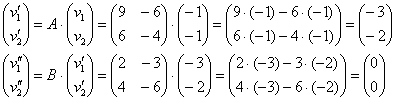
2) Найдём результирующее преобразование:
![]()
Таким образом:
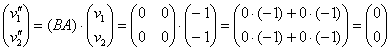
Ответ: ![]() (нулевой вектор)
(нулевой вектор)
Пример 6. Решение: используем формулу ![]() . Запишем матрицу перехода к новому базису:
. Запишем матрицу перехода к новому базису:
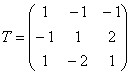
Найдём матрицу обратного перехода:

Вычислим:

Ответ: 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright