


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить определенный интеграл
по формуле трапеций и методом Симпсона?
Численные методы – достаточно большой раздел высшей математики и серьезные учебники по данной теме насчитывают сотни страниц. На практике, в контрольных работах традиционно предлагаются для решения некоторые задачи по численным методам, и одной из распространенных задач является – приближенное вычисление определенных интегралов. В этой статье я рассмотрю два метода приближенного вычисления определенного интеграла – метод трапеций и метод Симпсона.
Что нужно знать, чтобы освоить данные методы? Прозвучит забавно, но можно вообще не уметь брать интегралы. И даже вообще не понимать, что такое интегралы. Из технических средств потребуется микрокалькулятор. Да-да, нас ждут рутинные школьные расчёты. А еще лучше – закачайте мой калькулятор-полуавтомат для метода трапеций и метода Симпсона. Калькулятор написан в Экселе и позволит в десятки раз уменьшить время решения и оформления задач. Для экселевских чайников прилагается видеомануал! К слову, первая видеозапись с моим голосом.
Сначала зададимся вопросом, а зачем вообще нужны приближенные вычисления? Вроде бы можно найти первообразную функции и использовать формулу Ньютона-Лейбница, вычислив точное значение определенного интеграла. В качестве ответа на вопрос сразу рассмотрим демонстрационный пример с рисунком.
Вычислить определённый интеграл:
![]() .
.
Всё было бы хорошо, но в данном примере интеграл не берётся – перед вами неберущийся, так называемый интегральный логарифм. А существует ли вообще этот интеграл? Изобразим на чертеже график подынтегральной функции ![]() :
:
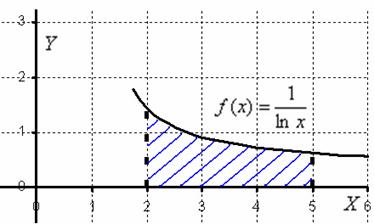
Всё нормально. Подынтегральная функция непрерывна на отрезке ![]() и определенный интеграл
и определенный интеграл ![]() численно равен заштрихованной площади. Да вот только одна загвоздка – интеграл не берётся. И в подобных случаях на помощь как раз приходят численные методы. При этом задача встречается в двух формулировках:
численно равен заштрихованной площади. Да вот только одна загвоздка – интеграл не берётся. И в подобных случаях на помощь как раз приходят численные методы. При этом задача встречается в двух формулировках:
1) Вычислить определенный интеграл приближенно, округляя результат до определённого знака после запятой. Например, до двух знаков после запятой, до трёх знаков после запятой и т.д. Предположим, получился приближенный ответ 5,347. На самом деле он может быть не совсем верным (в действительности, скажем, более точный ответ 5,343). Наша задача состоит лишь в том, чтобы округлить результат до трёх знаков после запятой.
2) Вычислить определенный интеграл приближенно, с определённой точностью. Например, вычислить определённый интеграл приближенно с точностью до 0,001. Что это значит? Это значит, мы должны отыскать такое приближенное значение, которое по модулю (в ту или другую сторону) отличается от истины не более чем на 0,001.
Существуют несколько основных методов приближенного вычисления определенного интеграла, который встречается в задачах:
Метод прямоугольников. Отрезок интегрирования разбивается на несколько частей и строится ступенчатая фигура, которая по площади близка к искомой площади:

Не судите строго за чертежи, точность не идеальна – они лишь помогают понять суть методов.
В данном примере проведено разбиение отрезка интегрирования ![]() на три отрезка:
на три отрезка:
![]() . Очевидно, что чем чаще разбиение (больше более мелких промежуточных отрезков), тем выше точность. «Ступенчатое» приближение является самым простым, и, видимо, поэтому довольно редко встречается в практических задачах. Тем не менее, методу прямоугольников посвящен отдельный урок, который «исторически» был создан намного позже этой статьи. Само собой, желательно пройтись по ссылке, но если метод не нужен/вы не хотите/нет времени, то можно читать дальше, единственное, останетесь без фильма =)
. Очевидно, что чем чаще разбиение (больше более мелких промежуточных отрезков), тем выше точность. «Ступенчатое» приближение является самым простым, и, видимо, поэтому довольно редко встречается в практических задачах. Тем не менее, методу прямоугольников посвящен отдельный урок, который «исторически» был создан намного позже этой статьи. Само собой, желательно пройтись по ссылке, но если метод не нужен/вы не хотите/нет времени, то можно читать дальше, единственное, останетесь без фильма =)
Метод трапеций. Идея аналогична. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается ломаной линией:
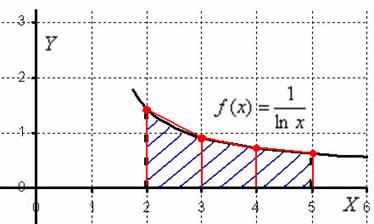
Таким образом, наша площадь (синяя штриховка) приближается суммой площадей трапеций (красный цвет). Отсюда и название метода. Легко заметить, что метод трапеций даёт значительно лучшее приближение, чем метод прямоугольников (при одинаковом количестве отрезков разбиения). И, естественно, чем больше более мелких промежуточных отрезков мы рассмотрим, тем будет выше точность. Метод трапеций время от времени встречается в практических заданиях, и в данной статье будет разобрано несколько примеров.
Метод Симпсона (метод парабол). Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболками. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций.
Чертеж строить не вижу смысла, поскольку визуально приближение будет накладываться на график функции ![]() (ломаная линия предыдущего пункта – и то практически совпала).
(ломаная линия предыдущего пункта – и то практически совпала).
Задача на вычисление определенного интеграла по формуле Симпсона – самая популярное задание на практике. И методу парабол будет уделено значительное внимание.
Как вычислить определенный интеграл методом трапеций?
Сначала формула в общем виде. Возможно, она будет не всем и не сразу понятна… да Карлссон с вами – практические примеры всё прояснят! Спокойствие. Только спокойствие.
Рассмотрим определенный интеграл 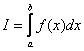 , где
, где ![]() – функция, непрерывная на отрезке
– функция, непрерывная на отрезке ![]() . Проведём разбиение отрезка
. Проведём разбиение отрезка ![]() на
на ![]() равных отрезков:
равных отрезков:
![]() . При этом, очевидно:
. При этом, очевидно: ![]() (нижний предел интегрирования) и
(нижний предел интегрирования) и ![]() (верхний предел интегрирования). Точки
(верхний предел интегрирования). Точки ![]() также называют узлами.
также называют узлами.
Тогда определенный интеграл можно вычислить приближенно по формуле трапеций:
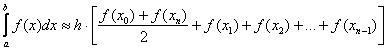 , где:
, где:
![]() – длина каждого из маленьких отрезков или шаг;
– длина каждого из маленьких отрезков или шаг;
![]() – значения подынтегральной функции в точках
– значения подынтегральной функции в точках ![]() .
.
Пример 1
Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.
![]()
а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.
Решение:
а) Специально для чайников я привязал первый пункт к чертежу, который наглядно демонстрировал принцип метода. Если будет трудно, посматривайте на чертёж по ходу комментариев, вот его кусок:
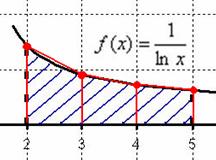
По условию отрезок интегрирования нужно разделить на 3 части, то есть ![]() .
.
Вычислим длину каждого отрезка разбиения: ![]() . Параметр
. Параметр ![]() , напоминаю, также называют шагом.
, напоминаю, также называют шагом.
Сколько будет точек ![]() (узлов разбиения)? Их будет на одну больше, чем количество отрезков:
(узлов разбиения)? Их будет на одну больше, чем количество отрезков:
![]()
Ну а общая формула трапеций сокращается до приятных размеров:
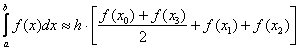
Для расчетов можно использовать обычный микрокалькулятор:
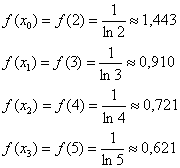
Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-го знака после запятой.
Окончательно:
![]()
С геометрической точки зрения мы вычислили сумму площадей трёх трапеций (см. рис. выше).
б) Разобьём отрезок интегрирования на 5 равных частей, то есть ![]() . Зачем это нужно? Чтобы Фобос-Грунт не падал в океан – увеличивая количество отрезков, мы увеличиваем точность вычислений.
. Зачем это нужно? Чтобы Фобос-Грунт не падал в океан – увеличивая количество отрезков, мы увеличиваем точность вычислений.
Если ![]() , то формула трапеций принимает следующий вид:
, то формула трапеций принимает следующий вид:
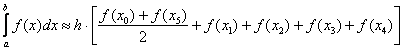
Найдем шаг разбиения:
![]() , то есть, длина каждого промежуточного отрезка равна 0,6.
, то есть, длина каждого промежуточного отрезка равна 0,6.
При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:

В первой строке записываем «счётчик».
Как формируется вторая строка, думаю, всем видно – сначала записываем нижний предел интегрирования ![]() , остальные значения получаем, последовательно приплюсовывая шаг
, остальные значения получаем, последовательно приплюсовывая шаг ![]() .
.
По какому принципу заполняется нижняя строка, тоже, думаю, практически все поняли. Например, если ![]() , то
, то ![]() . Что называется, считай, не ленись.
. Что называется, считай, не ленись.
В результате:

Ну что же, уточнение, и серьёзное, действительно есть! Если для 3 отрезков разбиения приближённое значение составило![]() , то для 5 отрезков
, то для 5 отрезков ![]() . Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере
. Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере ![]() .
.
Пример 2
Вычислить приближенно определенный интеграл по формуле трапеций с точностью до двух знаков после запятой (до 0,01).
![]()
Решение: Почти та же задача, но немного в другой формулировке. Принципиальное отличие от Примера 1 состоит в том, что мы не знаем, НА СКОЛЬКО отрезков разбивать отрезок интегрирования, чтобы получить два верных знака после запятой. Иными словами, мы не знаем значение ![]() .
.
Существует специальная формула, позволяющая определить количество отрезков разбиения, чтобы гарантированно достигнуть требуемой точности, но практике она часто трудноприменима. Поэтому выгодно использовать упрощенный подход.
Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 2-3-4-5. Разобьем отрезок интегрирования, например, на те же 5 частей. Формула уже знакома:
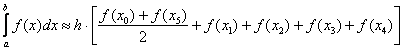
И шаг, естественно, тоже известен: ![]()
Но возникает еще один вопрос, до какого разряда округлять результаты ![]() ? В условии же ничего не сказано о том, сколько оставлять знаков после запятой. Общая рекомендация такова: к требуемой точности нужно прибавить 2-3 разряда. В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):
? В условии же ничего не сказано о том, сколько оставлять знаков после запятой. Общая рекомендация такова: к требуемой точности нужно прибавить 2-3 разряда. В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):

В результате:
![]() , обозначим приближение через
, обозначим приближение через ![]() .
.
После первичного результата количество отрезков удваивают. В данном случае необходимо провести разбиение на 10 отрезков. И когда количество отрезков растёт, то в голову приходит светлая мысль, что тыкать пальцами в микрокалькулятор уже как-то надоело. Поэтому еще раз предлагаю закачать и использовать мой калькулятор-полуавтомат (ссылка в начале урока).
Для ![]() формула трапеций приобретает следующий вид:
формула трапеций приобретает следующий вид:
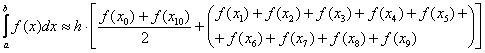
В бумажной версии запись можно спокойно перенести на следующую строчку.
Вычислим шаг разбиения: ![]()
Результаты расчётов сведём в таблицу:
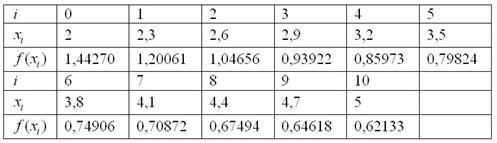
При чистовом оформлении в тетрадь длинную таблицу выгодно превратить в двухэтажную.
В результате:
![]()
Теперь вычислим расхождение между приближениями:
![]()
Здесь используем знак модуля, поскольку нас интересует абсолютная разность, а не какой результат больше, а какой – меньше.
Что касается дальнейших действий, то лично мне на практике встречалось 2 пути решения:
1) Первый способ – это «сравнение в лоб». Поскольку полученная оценка погрешности больше, чем требуемая точность:![]() , то необходимо ещё раз удвоить количество отрезков разбиения до
, то необходимо ещё раз удвоить количество отрезков разбиения до ![]() и вычислить уже
и вычислить уже ![]() . С помощью экселевского калькулятора готовый результат можно получить в считанные секунды:
. С помощью экселевского калькулятора готовый результат можно получить в считанные секунды: ![]() . Теперь снова оцениваем погрешность:
. Теперь снова оцениваем погрешность: ![]() . Полученная оценка меньше, чем требуемая точность:
. Полученная оценка меньше, чем требуемая точность: ![]() , следовательно, вычисления закончены. Осталось округлить последний (наиболее точный) результат
, следовательно, вычисления закончены. Осталось округлить последний (наиболее точный) результат ![]() до двух знаков после запятой и дать ответ.
до двух знаков после запятой и дать ответ.
2) Другой, более эффективный способ основан на применении так называемого правила Рунге, согласно которому мы ошибаемся в оценке определённого интеграла на самом деле не более чем на ![]() . В нашей задаче:
. В нашей задаче: ![]() , таким образом, надобность в вычислении
, таким образом, надобность в вычислении ![]() отпадает. Однако за скорость решения в данном случае пришлось расплатиться точностью:
отпадает. Однако за скорость решения в данном случае пришлось расплатиться точностью: ![]() . Тем не менее, такой результат приемлем, поскольку наш «лимит на ошибку» как раз и составляет одну сотую.
. Тем не менее, такой результат приемлем, поскольку наш «лимит на ошибку» как раз и составляет одну сотую.
Что выбрать? Ориентируйтесь на вашу методичку или предпочтения преподавателя.
Ответ: ![]() с точностью до 0,01 (
с точностью до 0,01 (![]() при использовании правила Рунге).
при использовании правила Рунге).
Пример 3
Вычислить приближенно определенный интеграл по формуле трапеций с точностью до 0,001.

Перед вами опять неберущийся интеграл (почти интегральный косинус). В образце решения на первом шаге проведено разбиение на 4 отрезка, то есть ![]() . Полное решение и примерный образец чистового оформления в конце урока.
. Полное решение и примерный образец чистового оформления в конце урока.
Как вычислить определенный интеграл по формуле Симпсона?
Если вы искали на данной страничке только метод Симпсона, то настоятельно рекомендую сначала прочитать начало урока и просмотреть хотя бы первый пример. По той причине, что многие идеи и технические приемы будут схожими с методом трапеций.
И снова, начнём с общей формулы.
Рассмотрим определенный интеграл  , где
, где ![]() – функция, непрерывная на отрезке
– функция, непрерывная на отрезке ![]() . Проведём разбиение отрезка
. Проведём разбиение отрезка ![]() на чётное количество равных отрезков. Чётное количество отрезков обозначают через
на чётное количество равных отрезков. Чётное количество отрезков обозначают через ![]() .
.
На практике отрезков может быть:
два: ![]()
четыре: ![]()
восемь: ![]()
десять: ![]()
двадцать: ![]()
Другие варианты не припоминаю.
Внимание! Число ![]() понимается как ЕДИНОЕ ЧИСЛО. То есть, НЕЛЬЗЯ сокращать, например,
понимается как ЕДИНОЕ ЧИСЛО. То есть, НЕЛЬЗЯ сокращать, например, ![]() на два, получая
на два, получая ![]() . Запись
. Запись ![]() лишь обозначает, что количество отрезков чётно. И ни о каких сокращениях речи не идёт
лишь обозначает, что количество отрезков чётно. И ни о каких сокращениях речи не идёт
Итак, наше разбиение имеет следующий вид:
![]()
Термины аналогичны терминам метода трапеций:
Точки ![]() называют узлами.
называют узлами.
Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид:
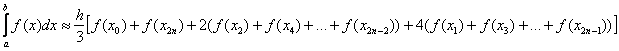 , где:
, где:
![]() – длина каждого из маленьких отрезков или шаг;
– длина каждого из маленьких отрезков или шаг;
![]() – значения подынтегральной функции в точках
– значения подынтегральной функции в точках ![]() .
.
Детализируя это нагромождение, разберу формулу подробнее:
![]() – сумма первого и последнего значения подынтегральной функции;
– сумма первого и последнего значения подынтегральной функции;
![]() – сумма членов с чётными индексами умножается на 2;
– сумма членов с чётными индексами умножается на 2;
![]() – сумма членов с нечётными индексами умножается на 4.
– сумма членов с нечётными индексами умножается на 4.
Пример 4
Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков ![]()
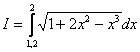
Интеграл, кстати, опять неберущийся.
Решение: Сразу обращаю внимание на тип задания – необходимо вычислить определенный интеграл с определенной точностью. Что это значит, уже комментировалось в начале статьи, а также на конкретных примерах предыдущего параграфа. Как и для метода трапеций, существует формула, которая сразу позволит определить нужное количество отрезков (значение «эн») чтобы гарантированно достичь требуемой точности. Правда, придётся находить четвертую производную и решать экстремальную задачу. Кто понял, о чём я, и оценил объем работы, тот улыбнулся. Однако здесь не до смеха, находить четвертую производную от такой подынтегральной функции будет уже не мегаботан, а клинический психопат. Поэтому на практике практически всегда используется упрощенный метод оценки погрешности.
Начинаем решать. Если у нас два отрезка разбиения ![]() , то узлов будет на один больше:
, то узлов будет на один больше: ![]() . И формула Симпсона принимает весьма компактный вид:
. И формула Симпсона принимает весьма компактный вид:
![]()
Вычислим шаг разбиения: ![]()
Заполним расчетную таблицу:
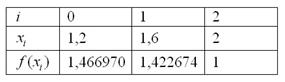
Еще раз комментирую, как заполняется таблица:
В верхнюю строку записываем «счётчик» индексов
Во второй строке сначала пишем нижний предел интегрирования ![]() , а затем последовательно приплюсовываем шаг
, а затем последовательно приплюсовываем шаг ![]() .
.
В третью строку заносим значения подынтегральной функции. Например, если ![]() , то
, то ![]() . Сколько оставлять знаков после запятой? Действительно, в условии опять об этом ничего не сказано. Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой.
. Сколько оставлять знаков после запятой? Действительно, в условии опять об этом ничего не сказано. Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой.
В результате:
![]()
Первичный результат получен. Теперь удваиваем количество отрезков до четырёх: ![]() . Формула Симпсона для данного разбиения принимает следующий вид:
. Формула Симпсона для данного разбиения принимает следующий вид:
![]()
Вычислим шаг разбиения: ![]()
Заполним расчетную таблицу:

Таким образом:
![]()
Найдём абсолютное значение разности между приближениями:
![]()
Правило Рунге для метода Симпсона очень вкусное. Если при использовании метода средних прямоугольников и метода трапеций нам даётся «поблажка» в одну треть, то сейчас – аж в одну пятнадцатую:
![]() , и точность здесь уже не страдает:
, и точность здесь уже не страдает:
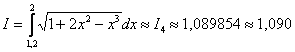
Но для полноты картины я приведу и «простецкое» решение, где придётся сделать дополнительный шаг: так как ![]() больше требуемой точности:
больше требуемой точности: ![]() , то необходимо еще раз удвоить количество отрезков:
, то необходимо еще раз удвоить количество отрезков: ![]() .
.
Формула Симпсона растёт, как на дрожжах:
![]()
Вычислим шаг: ![]()
И снова заполним расчетную таблицу:

Таким образом:
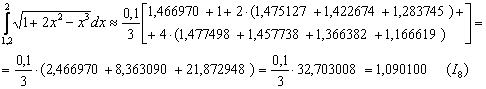
Заметьте, что здесь вычисления желательно уже расписать более подробно, поскольку формула Симпсона достаточно громоздка, и если сразу бУхнуть:
![]() , то выглядеть сиё бухло будет как халтура. А при более детальной записи у преподавателя сложится благостное впечатление, что вы добросовестно стирали клавиши микрокалькулятора в течение доброго часа. Детальные вычисления для «тяжелых» случаев присутствуют в моём калькуляторе.
, то выглядеть сиё бухло будет как халтура. А при более детальной записи у преподавателя сложится благостное впечатление, что вы добросовестно стирали клавиши микрокалькулятора в течение доброго часа. Детальные вычисления для «тяжелых» случаев присутствуют в моём калькуляторе.
Оцениваем погрешность:
![]()
Погрешность меньше требуемой точности: ![]() . Осталось взять наиболее точное приближение
. Осталось взять наиболее точное приближение ![]() , округлить его до трёх знаков после запятой и записать:
, округлить его до трёх знаков после запятой и записать:
Ответ:  с точностью до 0,001
с точностью до 0,001
Пример 5
Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,0001. Разбиение начать с двух отрезков ![]()
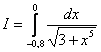
Это пример для самостоятельного решения. Примерный образец чистового оформления и ответ в конце урока.
В заключительной части урока рассмотрим еще пару распространенных примеров:
Пример 6
Вычислить приближенное значение определенного интеграла ![]() с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой.
Решение: обратите внимание, что здесь следует провести лишь округление, а уж насколько точным окажется приближение – совершенно не важно.
Используем формулу Симпсона:
![]()
При десяти отрезках разбиения ![]() шаг составляет
шаг составляет ![]()
Заполним расчетную таблицу:
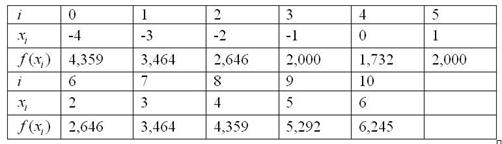
Чтобы не пришлось «мельчить» и всё разборчиво вместилось на тетрадный лист – таблицу рациональнее сделать двухэтажной.
Вычисления, не ленимся, расписываем подробно:

Ответ: ![]()
И еще раз подчеркну, что о точности здесь речи не идет. На самом деле, ответ может быть не ![]() , а, условно говоря,
, а, условно говоря, ![]() . В этой связи в ответе не нужно машинально приписывать «дежурную» концовку: «с точностью до 0,001».
. В этой связи в ответе не нужно машинально приписывать «дежурную» концовку: «с точностью до 0,001».
Интересно отметить, что данный интеграл берётся, правда, новичку взломать его не так-то просто (соответствующий метод решения рассмотрен в Примере 5 урока Сложные интегралы). Любознательные студенты могут вычислить предложенный интеграл по формуле Ньютона-Лейбница и найти ТОЧНУЮ абсолютную погрешность найденного приближенного значения.
Для самостоятельного решения:
Пример 7
Вычислить приближенное значение определенного интеграла ![]() с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой..
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления проводить с точностью до третьего знака после запятой..
Примерная версия чистового оформления и ответ в конце урока, который подошел к концу.
Для приближенного вычисления определенного интеграла применяются и другие методы. В частности, теория степенных рядов со стандартной задачей Приближенное вычисление определенного интеграла путём разложения подынтегральной функции в ряд. Но это уже материал второго курса.
А сейчас настала пора раскрыть страшную тайну интегрального исчисления. Я создал около двух десятков уроков по интегралам, и это, так скажем, классика темы. На практике же, в частности, при инженерных расчетах – приблизить объекты реального мира стандартными математическими функциями практически невозможно. Невозможно идеально точно рассчитать, площадь, объем, плотность, к примеру, асфальтового покрытия. Погрешность, пусть с десятого, пусть с сотого знака после запятой – но она всё равно будет. Именно поэтому по приближенным методам вычисления написаны сотни увесистых кирпичей и создано серьёзное программное обеспечение для приближенных вычислений. Классическая же теория интегрального исчисления в действительности применяется заметно реже. Но, кстати, без неё – тоже никуда!
Данный урок не рекорден по объему, но на его создание у меня ушло необычно много времени. Я правил материал и переделывал структуру статьи несколько раз, поскольку постоянно прорисовывались новые нюансы и тонкости. Надеюсь, труды были не напрасны, и получилось вполне логично и доступно.
Всего вам доброго!
Решения и ответы:
Пример 3: Решение: Разбиваем отрезок интегрирования на 4 части: ![]()
Тогда формула трапеций принимает следующий вид:
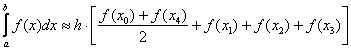
Вычислим шаг: ![]()
Заполним расчетную таблицу:

Таким образом:
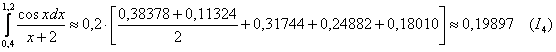
Удвоим количество отрезков: ![]()
Вычислим шаг: ![]()
Заполним расчетную таблицу:

Таким образом:
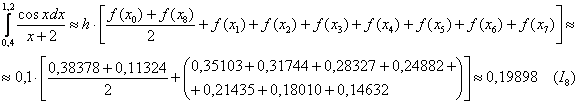
Оценим погрешность вычислений:
![]() , таким образом, требуемая точность достигнута.
, таким образом, требуемая точность достигнута.
Примечание: и тем более она достигнута по правилу Рунге.
Ответ:  с точностью до 0,001
с точностью до 0,001
Пример 5: Решение: 1) Рассмотрим два отрезка разбиения ![]()
Вычислим шаг: ![]()
Заполним расчетную таблицу:
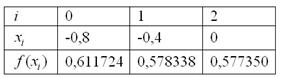
Таким образом:
![]()
2) Рассмотрим четыре отрезка разбиения ![]()
Вычислим шаг: ![]()
Заполним расчетную таблицу:

Таким образом:

Оценим погрешность:
![]()
Примечание: если оценку проводить по правилу Рунге, то:
![]() , то есть вычисления закончены и дополнительного шага не требуется.
, то есть вычисления закончены и дополнительного шага не требуется.
2) Рассмотрим восемь отрезков разбиения ![]()
Вычислим шаг: ![]()
Заполним расчетную таблицу:

Таким образом:

Оценим погрешность:
![]()
Ответ:  с точностью до 0,0001
с точностью до 0,0001
Пример 7: Решение: Используем формулу Симпсона:
![]() , где:
, где: ![]() ,
, ![]() ,
, ![]()
В данном случае: ![]()

Таким образом:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright