


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Простейшие типовые задачи с производной. Примеры решений
После изучения азов нахождения производной в статьях Как найти производную? Примеры решений и Производная сложной функции мы рассмотрим типовые задачи, связанные с нахождением производной. Желающие улучшить свои навыки дифференцирования также могут ознакомиться с уроком Сложные производные. Логарифмическая производная.
Помимо нового материала у вас есть возможность дополнительно «набить руку» на нахождении производных. Действительно, если речь пойдет о типовых задачах на производную, то, как минимум, во всех примерах нужно будет найти эту самую производную. Я постараюсь рассмотреть приёмы решения и хитрости, которые не встречались в других статьях.
Вот наше аппетитное меню:
- Производная функции в точке
- Уравнение касательной к графику функции в точке
- Дифференциал функции одной переменной
- Вторая производная
Повар на раздаче.
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Пример 1
Вычислить производную функции ![]() в точке
в точке ![]()
Справка: Следующие способы обозначения функции эквивалентны:
![]()
![]()
В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
![]()
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке ![]() :
:
![]()
Готово.
Небольшой разминочный пример для самостоятельного решения:
Пример 2
Вычислить производную функции ![]() в точке
в точке ![]()
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Пример 3
Вычислить производную функции ![]() в точке
в точке ![]() .
.
Сначала найдем производную:
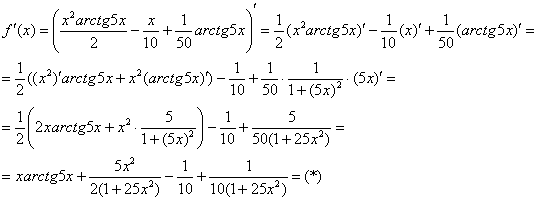
Производная, в принципе, найдена, и можно подставлять требуемое значение ![]() . Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
. Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
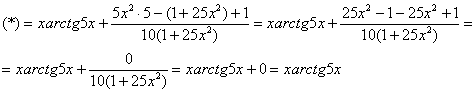
Ну вот, совсем другое дело. Вычислим значение производной в точке ![]() :
:
![]()
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому что арктангенсов на студенческий век ещё хватит.
Пример 4
Вычислить производную функции ![]() в точке
в точке ![]() .
.
Это пример для самостоятельного решения.
Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной к графику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
Составить уравнение касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() . Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):
. Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):
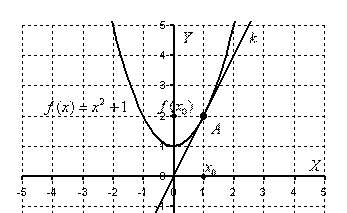
Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственной точке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.
Применительно к нашему случаю: при ![]() касательная
касательная ![]() (стандартное обозначение) касается графика функции в единственной точке
(стандартное обозначение) касается графика функции в единственной точке ![]() .
.
И наша задача состоит в том, чтобы найти уравнение прямой ![]() .
.
Как составить уравнение касательной в точке с абсциссой 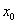 ?
?
Общая формула знакома нам еще со школы:
![]()
Значение ![]() нам уже дано в условии.
нам уже дано в условии.
Теперь нужно вычислить, чему равна сама функция в точке ![]() :
:
![]()
На следующем этапе находим производную:
![]()
Находим производную в точке (задание, которое мы недавно рассмотрели):
![]()
Подставляем значения ![]() ,
, ![]() и
и ![]() в формулу
в формулу ![]() :
:
![]()
![]()
Таким образом, уравнение касательной:
![]()
Это «школьный» вид уравнения прямой с угловым коэффициентом. В высшей математике уравнение прямой на плоскости принято записывать в так называемой общей форме ![]() , поэтому перепишем найденное уравнение касательной в соответствии с традицией:
, поэтому перепишем найденное уравнение касательной в соответствии с традицией:
![]()
Очевидно, что точка ![]() должна удовлетворять данному уравнению:
должна удовлетворять данному уравнению:
![]()
![]() – верное равенство.
– верное равенство.
Следует отметить, что такая проверка является лишь частичной. Если мы неправильно вычислили производную в точке ![]() , то выполненная подстановка нам ничем не поможет.
, то выполненная подстановка нам ничем не поможет.
Рассмотрим еще два примера.
Пример 5
Составить уравнение касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]()
Уравнение касательной составим по формуле ![]()
1) Вычислим значение функции в точке ![]() :
:
![]()
2) Найдем производную. Дважды используем правило дифференцирования сложной функции:
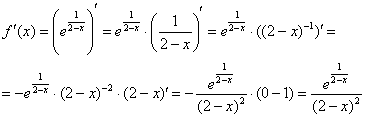
3) Вычислим значение производной в точке ![]() :
:
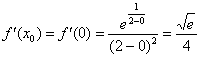
4) Подставим значения ![]() ,
, ![]() и
и ![]() в формулу
в формулу ![]() :
:
![]()
![]()
![]()
![]()
![]()
Готово.
Выполним частичную проверку:
Подставим точку ![]() в найденное уравнение:
в найденное уравнение:
![]()
![]() – верное равенство.
– верное равенство.
Пример 6
Составить уравнение касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]()
Полное решение и образец оформления в конце урока.
В задаче на нахождение уравнения касательной очень важно ВНИМАТЕЛЬНО и аккуратно выполнить вычисления, привести уравнение прямой к общему виду. И, конечно же, ознакомьтесь со строгим определением касательной, после чего закрепите материал на уроке Уравнение нормали, где есть дополнительные примеры с касательной.
Дифференциал функции одной переменной
С формально-технической точки зрения найти дифференциал функции – это «почти то же самое, что найти производную».
Производная функции чаще всего обозначается через ![]() .
.
Дифференциал функции стандартно обозначается через ![]() (так и читается – «дэ игрек»)
(так и читается – «дэ игрек»)
Дифференциал функции одной переменной записывается в следующем виде:
![]()
Другой вариант записи: ![]()
Простейшая задача: Найти дифференциал функции ![]()
1) Первый этап. Найдем производную:
![]()
2) Второй этап. Запишем дифференциал:
![]()
Готово.
Дифференциал функции одной или нескольких переменных чаще всего используют для приближенных вычислений.
Помимо «комбинированных» задач с дифференциалом время от времени встречается и «чистое» задание на нахождение дифференциала функции:
Пример 7
Найти дифференциал функции 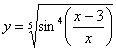
Перед тем, как находить производную или дифференциал, всегда целесообразно посмотреть, а нельзя ли как-нибудь упростить функцию (или запись функции) ещё до дифференцирования? Смотрим на наш пример. Во-первых, можно преобразовать корень:
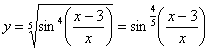 (корень пятой степени относится именно к синусу).
(корень пятой степени относится именно к синусу).
Во-вторых, замечаем, что под синусом у нас дробь, которую, очевидно, предстоит дифференцировать. Формула дифференцирования дроби очень громоздка. Нельзя ли избавиться от дроби? В данном случае – можно, почленно разделим числитель на знаменатель:
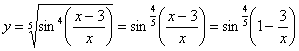
Функция сложная. В ней два вложения: под степень вложен синус, а под синус вложено выражение ![]() . Найдем производную, используя правило дифференцирования сложной функции
. Найдем производную, используя правило дифференцирования сложной функции ![]() два раза:
два раза:
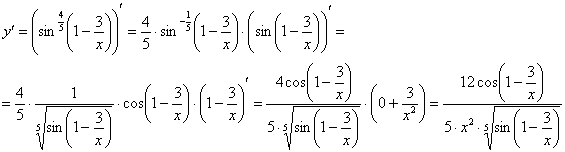
Запишем дифференциал, при этом снова представим ![]() в первоначальном «красивом» виде:
в первоначальном «красивом» виде:
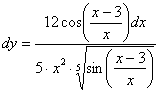
Готово.
Когда производная представляет собой дробь, значок ![]() обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).
обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).
Пример 8
Найти дифференциал функции ![]()
Это пример для самостоятельного решения.
Следующие два примера на нахождение дифференциала в точке:
Пример 9
Вычислить дифференциал функции ![]() в точке
в точке ![]()
Найдем производную:
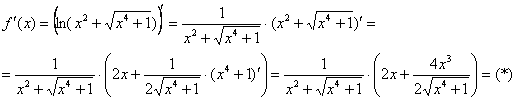
Опять, производная вроде бы найдена. Но в эту бодягу еще предстоит подставлять число, поэтому результат максимально упрощаем:
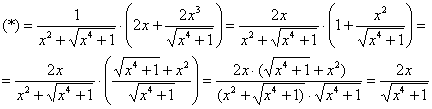
Труды были не напрасны, записываем дифференциал:
![]()
Теперь вычислим дифференциал в точке ![]() :
:
![]()
В значок дифференциала ![]() единицу подставлять не нужно, он немного из другой оперы.
единицу подставлять не нужно, он немного из другой оперы.
Ну и хорошим тоном в математике считается устранение иррациональности в знаменателе. Для этого домножим числитель и знаменатель на ![]() . Окончательно:
. Окончательно:
![]()
Пример 10
Вычислить дифференциал функции 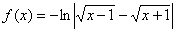 в точке
в точке ![]() . В ходе решения производную максимально упростить.
. В ходе решения производную максимально упростить.
Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.
Вторая производная
Всё очень просто. Вторая производная – это производная от первой производной: ![]()
Стандартные обозначения второй производной: ![]() ,
, ![]() или
или ![]() (дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите
(дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите ![]() функции…». А студент сидит и битый час чешет репу, что это вообще такое.
функции…». А студент сидит и битый час чешет репу, что это вообще такое.
Рассмотрим простейший пример. Найдем вторую производную от функции ![]() .
.
Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:
![]()
Теперь находим вторую производную:
![]()
Готово.
Рассмотрим более содержательные примеры.
Пример 11
Найти вторую производную функции ![]()
Найдем первую производную:
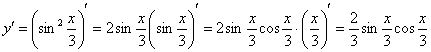
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности, применив известную тригонометрическую формулу ![]() . Точнее говоря, использовать формулу будем в обратном направлении:
. Точнее говоря, использовать формулу будем в обратном направлении: ![]() :
:
![]()
Находим вторую производную:
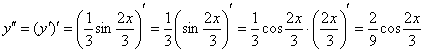
Готово.
Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу ![]() :
:
![]()
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.
Отмечу, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.
Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.
Например: Вычислим значение найденной второй производной в точке ![]() :
:
![]()
Необходимость находить вторую производную и вторую производную в точке возникает при исследовании графика функции на выпуклость/вогнутость и перегибы.
Пример 12
Найти вторую производную функции ![]() . Найти
. Найти ![]()
Это пример для самостоятельного решения.
Аналогично можно найти третью производную, а также производные более высоких порядков. Такие задания встречаются, но встречаются чуть реже.
Желаю успехов!
Решения и ответы:
Пример 2: Найдем производную:
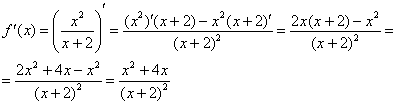
Вычислим значение функции в точке ![]() :
:
![]()
Пример 4: Найдем производную:
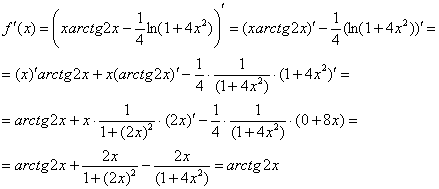
Вычислим производную в заданной точке:
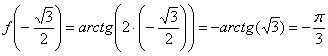
Пример 6: Уравнение касательной составим по формуле ![]()
1) Вычислим значение функции в точке ![]() :
:
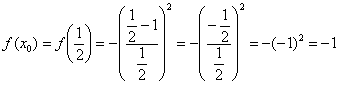
2) Найдем производную. Перед дифференцированием функцию выгодно упростить:
![]()
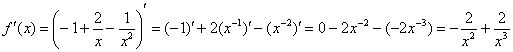
3) Вычислим значение производной в точке ![]() :
:
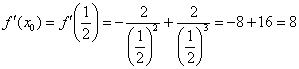
4) Подставим значения ![]() ,
, ![]() и
и ![]() в формулу
в формулу ![]() :
:
![]()
![]()
![]()
Пример 8: Преобразуем функцию:
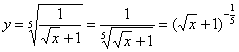
Найдем производную:

Запишем дифференциал:
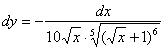
Пример 10: Найдем производную:
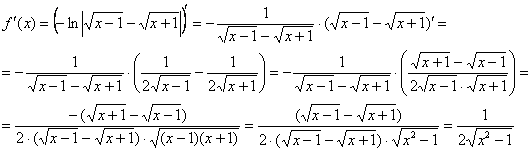
Запишем дифференциал:
![]()
Вычислим дифференциал в точке ![]() :
:
![]()
Пример 12: Найдем первую производную:
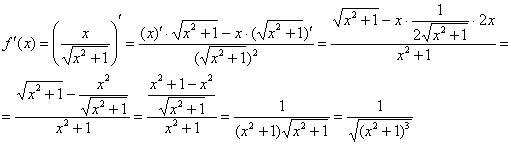
Найдем вторую производную:
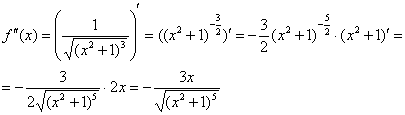
Вычислим: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright