Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

3. Интервальный вариационный ряд.
Гистограмма относительных частот

На предыдущем уроке по математической статистике (Занятие 1) мы разобрали дискретный вариационный ряд (Занятие 2), и сейчас на очереди интервальный. Его понятие, графическое представление (гистограмма и эмпирическая функция распределения), а также рациональные методы вычислений, как ручные, так и программные. В том числе будут рассмотрены задачи с достаточно большим количеством (100-200) вариант – что делать в таких случаях, как обработать большой массив данных. 

Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений. Зачастую ИВР появляется в результате измерения непрерывной характеристики изучаемых объектов. Типично – это время, масса, размеры и другие физические характеристики. Подходящие примеры встретились в первой же статье по матстату, вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.

Для изучения интервального вариационного ряда затруднительно либо невозможно применить тот же подход, что и для дискретного ряда. Это связано с тем, что ВСЕ варианты многих ИВР различны. И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, ибо полученные значения всё равно отличаются хоть какими-то микрограммами.

Поэтому для исследования ИВР используется другой подход, а именно, определяется интервал, в пределах которого варьируются значения, затем данный интервал делится на частичные интервалы, и по каждому интервалу подсчитываются частоты – количество вариант, которые в него попали.

Разберём всю кухню на конкретной задаче, и чтобы как-то разнообразить физику, я приведу пример с экономическим содержанием, кои десятками предлагают студентам экономических отделений. Деньги, строго говоря, дискретны, но если надо, непрерывны :), и по причине слишком большого разброса цен, для них целесообразно строить интервальный ряд:

Пример 6

По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах):

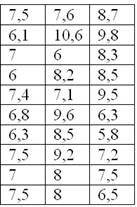
Требуется составить вариационный ряд распределения, построить гистограмму частот, гистограмму и полигон относительных частот + бонус – эмпирическую функцию распределения.

Такое обывательское исследование проводит каждый из нас, начиная с анализа цены на пакет молока вот это дожил в нескольких магазинах, и заканчивая ценами на недвижимость по гораздо бОльшей выборке. Что называется, не какие-то там унылые сантиметры.

Поэтому представьте свой любимый товар / услугу и наслаждайтесь решением:)

Очевидно, что перед нами выборочная совокупность объемом  наблюдений (таблица 10*3), и вопрос номер один: какой ряд составлять – дискретный или интервальный? Смотрим на таблицу: среди предложенных цен есть одинаковые, но их разброс довольно велик, и поэтому здесь целесообразно провести интервальное разбиение. К тому же цены могут быть округлёнными.

Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.

Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:

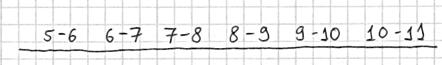
Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы:

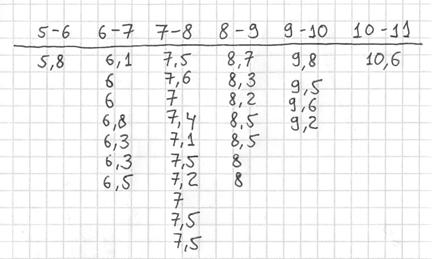
После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
  ден. ед. – хорошим тоном считается указывать размерность.

Вычислим размах вариации:
 ден. ед. – длина общего интервала, в пределах которого варьируется цена.

Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса: 

, где  – десятичный логарифм* от объёма выборки и  – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

* есть на любом более или менее приличном калькуляторе

В нашем случае получаем:
 интервалов.

Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
 – длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»: . Посему от самой малой варианты  отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины  (например, ) – они требуются почти во всех тематических задачах:

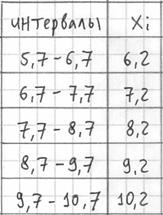
– убеждаемся в том, что самая большая варианта  вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем:

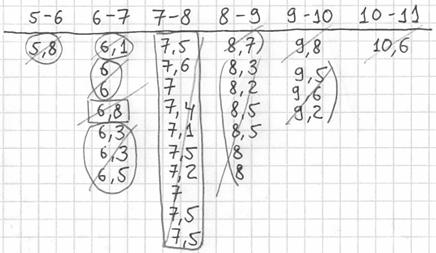
Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.

Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна:  – и её нужно причислить к интервалу .

В результате получаем интервальный вариационный ряд:

 при этом обязательно убеждаемся в том, что ничего не потеряно:
, ОК.

Изобразим ряд графически. Для этого по каждому интервалу нужно найти (не пугаемся): плотность частот , относительные частоты  (округляем их до 2 знаков после запятой), а также плотность относительных частот . Поскольку длина частичного интервала , то вычисления заметно упрощаются:

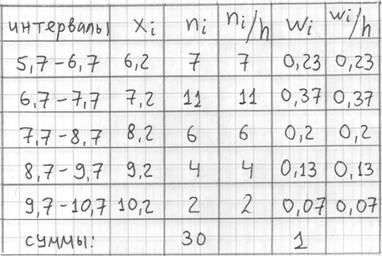
В том случае, если интервалы имеют разные длины , то при нахождении плотностей каждую частоту нужно делить на длину своего интервала: . Но у нас популярная равноинтервальная группировка, да не абы какая, а с единичным частичным интервалом. Возьмите на заметку всю выгоду такого интервала.

Дело за чертежами. Один за другим.

Гистограмма частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям частот:

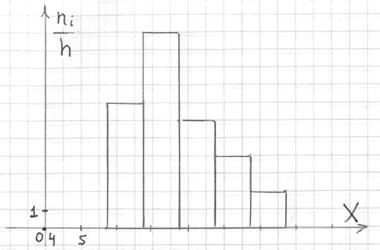
При этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх.

Площадь гистограммы частот в точности равна объёму совокупности: .  В нашем случае  и плотности  совпали с самими частотами , таким образом:

Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям относительных частот:

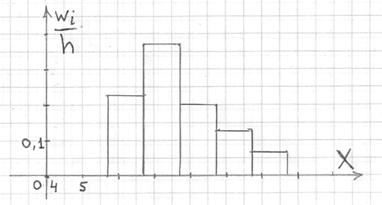
Площадь такой гистограммы равна единице: , и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.

И для ИВР чаще всего строят гистограмму именно относительных частот. А вместе с ней нередко и полигон таковых частот.  Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки , где  – середины интервалов:

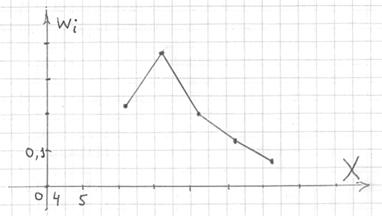
По сути, здесь мы приблизили интервальный ряд дискретным, выбрав в качестве вариант  середины интервалов. Это важнейший принцип и метод, который неоднократно встретится нам в последующих задачах.

Большим достоинством приведённого решения является тот факт, что многие вычисления здесь устные, а если вы помните, как делить «столбиком», то можно обойтись даже без калькулятора. Вот она где притаилась, смерть Терминатора :) ;)

Автоматизируем решение в Экселе:

  Как составить ИВР и представить его графически? (Ютуб)

И бонус – эмпирическая функция распределения. Она определяется точно так же, как в дискретном случае:

, где  – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.

Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:

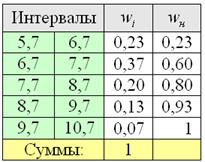
И строим кусочно-ломаную линию, с промежуточными точками , где  – правые концы интервалов, а  – относительная частота, которая успела накопиться на всех «пройденных» интервалах:

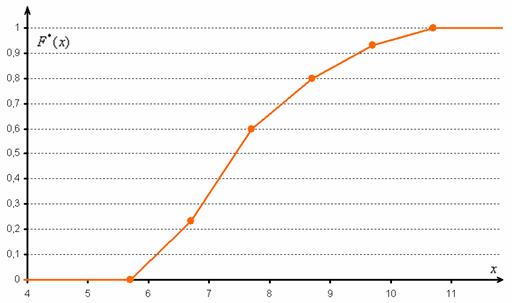
При этом  если  и  если .

Напоминаю, что данная функция не убывает, принимает значения из промежутка  и, кроме того, для ИВР она ещё и непрерывна.

Эмпирическая функция распределения является аналогом функции распределения НСВ и приближает теоретическую функцию , которую теоретически, а иногда и практически можно построить по всей генеральной совокупности.

Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и огивы частот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и поэтому о ней буквально пару абзацев:

Кумулята – это ломаная, соединяющая точки:

* либо  – для дискретного вариационного ряда;
 либо  – для интервального вариационного ряда.

*  – накопленные «обычные» частоты

В последнем случае кумулята относительных частот  представляет собой «главный кусок» недавно построенной эмпирической функции распределения.

Огива – это обратная функция по отношению к кумуляте – здесь варианты откладываются по оси ординат, а накопленные частоты либо относительные частоты – по оси абсцисс.

С построением данных линий, думаю, проблем быть не должно, чего не скажешь о другой проблеме. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать, если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Считаю нужным снять небольшое видео:

  Как быстро составить ИВР при большом объёме выборки? (Ютуб)

Ну, теперь вы монстры 8-го уровня :)

Но не всё так сурово. В большинстве задач вам предложат готовый вариационный ряд, и на счёт молока, то, конечно, была шутка:

Пример 7

Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения

Задание 3

Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается) И на всякий случай краткое решение для сверки в конце урока. Должен признаться, я немного усложнил это задание, сделав интервалы разной длины – для лучшего понимания материала.

Что ещё важного по теме? Время от времени встречаются ИВР с открытыми крайними интервалами, например:

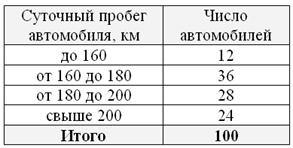
В таких случаях, что убийственно логично, интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала:  км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Тоже логично. Но уже не убийственно:) Если внутренние интервалы имеют разные длины, то для крайних интервалов можно взять среднюю арифметическую известных длин.

Ну вот, пожалуй, и вся практически важная информация по ИВР.

На очереди числовые характеристики вариационных рядов и начнём мы с их центральных характеристик, а именно – Моды, медианы и средней.

До скорых встреч!

Решения и ответы:

Пример 7. Решение: в данной задаче интервалы имеют разные длины , заполним расчётную таблицу:

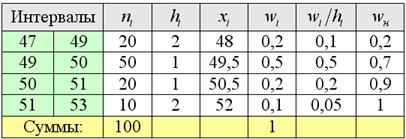
Построим гистограмму относительных частот:

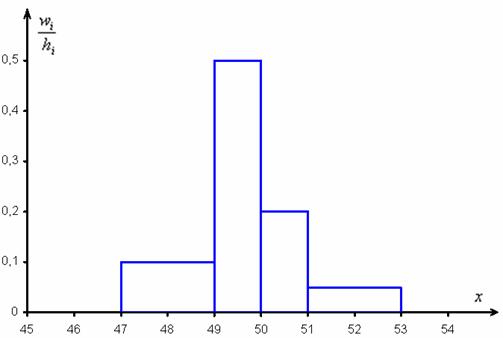
Построим полигон относительных частот:

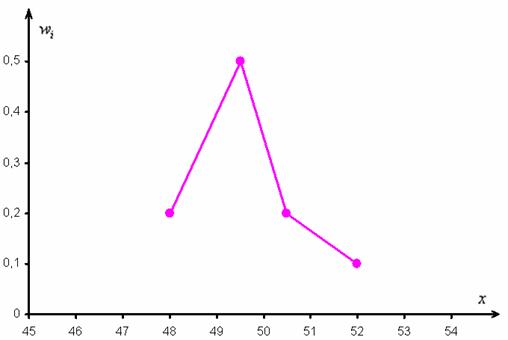
Построим эмпирическую функцию распределения:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте