Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Некоторые свойства операций над матрицами.
Матричные выражения

На базовых уроках Действия с матрицами, Как найти обратную матрицу? мы познакомились с понятием матрицы и основными операциями над матрицами. При этом основные акценты были подробно расставлены на технических приёмах вычисления, чтобы совершенно неподготовленный человек смог быстро научиться решать матрицы. Поэтому чайникам следует начать с первых двух статей и лягушатника с определителем матрицы. Из инструментальных средств рекомендую запастись матричным калькулятором, который позволит контролировать весь процесс решения и не допустить ошибок. Найти его можно, например, на складе математических формул и таблиц.

А сейчас последует продолжение темы, в котором мы рассмотрим не только новый материал, но и отработаем действия с матрицами.

Некоторые свойства операций над матрицами

Существует достаточно много свойств, которые касаются действий с матрицами, в той же Википедии можно полюбоваться стройными шеренгами соответствующих правил. Однако на практике многие свойства в известном смысле «мертвЫ», поскольку в ходе решения реальных задач используются лишь некоторые из них. Моя цель – рассмотреть прикладное применение свойств на конкретных примерах, и если вам необходима строгая теория, пожалуйста, воспользуйтесь другим источником информации.

Но сначала вернёмся к действиям с матрицами (к слову, в той статье мы уже неявно затронули ряд свойств). Начну с небольшого вопроса, который вызвал трудности у некоторых посетителей сайта:

Можно ли к матрице прибавить число?

Например: . Ну, или наоборот:

Нет. К матрице можно прибавить только другую матрицу, причём точно такого же размера.

Матрицу можно умножить на число. Но сложить их нельзя. Таковы правила игры.

Следует отметить, что допустимо сложение определителя матрицы с числом:

Результат вычисления определителя – число, а два числа суммируются без всяких проблем.

Вышесказанное, естественно, справедливо и для разности, ведь вычитание – это частный случай сложения.

Как на счёт того, чтобы плотно зависнуть у меня сегодня вечером? =) Практика показывает, что наибольшие трудности у студентов вызывает умножение матриц. Так наполним же кружки соответствующей информацией.

Повторим само правило. В статье Действия с матрицами я рассказал о том, какие матрицы можно умножать и привёл ряд наиболее распространённых примеров. Давайте рассмотрим операцию чуть подробнее и выделим два существенных пункта:

1) Смотрим на левую часть. Из первого урока нам известно, что матричное умножение возможно в том и только в том случае, если  количество столбцов первой матрицы равно количеству строк второй матрицы.

2) Смотрим на правую часть и обращаем внимание на размерность результата – СКОЛЬКО строк и столбцов должно быть у итоговой матрицы.

Пример 1

Умножить матрицы

Решение: произведение существует, причём итоговая матрица состоит из 1 строки и 2 столбцов:

Ответ:

Пример 2

Умножить матрицы

Это пример для самостоятельного решения.

Предложенные примеры не случайны. Они вроде бы просты, но у начинающих здесь нередко возникает путаница с размерами матрицы-результата. Поэтому читателям с небольшим опытом целесообразно переписать вышеприведённую формулу и особенно серьёзно отнестись к практическим примерам.

А по каким принципам составляются начинка (суммы произведений чисел), думаю, все уже поняли. Дополнительно возьмём на вооружение образную ассоциацию, которая поможет хорошо запомнить действие. Читаем следующий параграф:

Как возвести матрицу в квадрат?

Операция определена только для квадратных матриц – «два на два», «три на три» и т.д.

Возвести квадратную матрицу  в квадрат – это значит, умножить её саму на себя:

Пример 3

Возвести в квадрат матрицу

Решение: пример рутинный, и чтобы извлечь максимальную пользу, давайте закрепим очень распространённый случай умножения двух матриц «три на три»:

Строки первой матрицы – это столы в ресторане, а цветные столбцы второй матрицы – официанты. Сначала столы обслуживает красный официант, затем зелёный официант, и под конец застолья – синий официант. Тааак, хватит прикалываться, он не голубой =)

Это действительно удобный мысленный приём, который можно использовать на практике – последовательно (слева направо) перебираем столбцы второй матрицы  и «пристраиваем» их к каждой строке первой матрицы.

Ответ:

Возведение матрицы в куб и более высокие степени разберём позже.

Немного о некоммутативности матричного умножения и единичной матрице

Материал, по меньшей мере, частично вам знаком. Для тех, кто не знает термина:
Коммутативность = Перестановочность.

Обычные числа переставлять можно: , а матрицы в общем случае не перестановочны: . Собственно, подробная иллюстрация с конкретными примерами уже была дана в статье Действия с матрицами.

Рассмотрим некоторые исключения из правила, которые потребуются для выполнения практических задач.

Если у квадратной матрицы  существует обратная матрица , то их умножение коммутативно:

Чтобы проверить, правильно ли найдена обратная матрица, нужно вычислить произведение  либо произведение  и убедиться в том, что получится единичная матрица . Конкретные примеры можно посмотреть в статье Как найти обратную матрицу?

Единичной матрицей называется квадратная матрица, у которой на главной диагонали расположены единицы, а остальные элементы равны нулю. Например: ,  и т.д.

При этом справедливо следующее свойство: если произвольную матрицу  умножить слева или справа на единичную матрицу подходящих размеров, то в результате получится исходная матрица:

Как видите, здесь также имеет место коммутативность матричного умножения.

Возьмём какую-нибудь матрицу, ну, скажем, матрицу из предыдущей задачи: .

Желающие могут провести проверку и убедиться, что:

Единичная матрица для матриц – это аналог числовой единицы для чисел, что особенно хорошо видно из только что рассмотренных примеров.

Коммутативность числового множителя относительно умножения матриц

Для матриц  и действительного числа  справедливо следующее свойство:

То есть числовой множитель можно (и нужно) вынести вперёд, чтобы он «не мешал» умножить матрицы.

Примечание: вообще говоря, формулировка свойства неполная – «лямбду» можно разместить в любом месте между матрицами, хоть в конце. Правило остаётся справедливым, если перемножаются три либо бОльшее количество матриц.

Пример 4

Вычислить произведение

Решение:

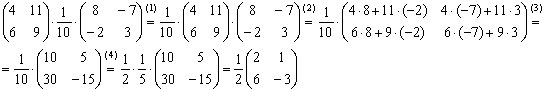
(1) Согласно свойству  перемещаем числовой множитель вперёд. Сами матрицы переставлять нельзя!

(2) – (3) Выполняем матричное умножение.

(4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на  .

Окончательный ответ лучше оставить в виде , хотя, в принципе, годится и внесение дроби: 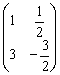. На технических тонкостях умножения матрицы на число я подробно останавливался на уроке Действия с матрицами.

Ответ:

Маленькая шарада для самостоятельного решения:

Пример 5

Вычислить , если 

Решение и ответ в конце урока.

Какой технический приём важен в ходе решения подобных примеров? С числом разбираемся в последнюю очередь.

Прицепим к локомотиву ещё один вагон:

Как умножить три матрицы?

Прежде всего, ЧТО должно получиться в результате умножения трёх матриц ?  Кошка не родит мышку. Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =)

Произведение трёх матриц  можно вычислить двумя способами:

1) найти , а затем домножить на матрицу «цэ»: ;

2) либо сначала найти , потом выполнить умножение .

Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения:

Пример 6

Перемножить матрицы двумя способами

Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц.

1) Используем формулу

Действие первое:

Действие второе:

2) Используем формулу

Действие первое:

Действие второе:

Ответ:

Более привычен и стандартен, конечно же, первый способ решения, там «как бы всё по порядку». Кстати, по поводу порядка. В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ. Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет.

Свойство ассоциативности умножения справедливо не только для квадратных, но и для произвольных матриц – лишь бы они умножались:

Пример 7

Найти произведение трёх матриц 

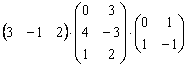
Это пример для самостоятельного решения. В образце решения вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.

Свойство ассоциативности матричного умножения имеет место быть и для бОльшего количества множителей.

Теперь самое время вернуться к степеням матриц. Квадрат матрицы рассмотрен в самом начале и на повестке дня вопрос:

Как возвести матрицу в куб и более высокие степени?

Данные операции также определены только для квадратных матриц. Чтобы возвести квадратную матрицу  в куб, нужно вычислить произведение:

Фактически это частный случай умножения трёх матриц, по свойству ассоциативности матричного умножения: . А матрица, умноженная сама на себя – это квадрат матрицы:

Таким образом, получаем рабочую формулу:

То есть задание выполняется в два шага: сначала матрицу необходимо возвести в квадрат, а затем полученную матрицу  умножить на матрицу .

Пример 8

Возвести матрицу  в куб.

Это небольшая задачка для самостоятельного решения.

Возведение матрицы в четвёртую степень проводится закономерным образом:

Используя ассоциативность матричного умножения, выведем две рабочие формулы.  Во-первых:  – это произведение трёх матриц.

1) . Иными словами, сначала находим , затем  домножаем его на «бэ» –  получаем куб, и, наконец, выполняем умножение ещё раз – будет четвёртая степень.

2) Но существует решение на шаг короче: . То есть, на первом шаге находим квадрат  и, минуя куб, выполняем умножение

Дополнительное задание к Примеру 8:

Возвести матрицу  в четвёртую степень.

Как только что отмечалось, сделать это можно двумя способами:

1) Коль скоро известен куб, то выполняем умножение .

2) Однако, если по условию задачи требуется возвести матрицу только в четвёртую степень, то путь выгодно сократить – найти квадрат матрицы и воспользоваться формулой .

Оба варианта решения и ответ – в конце урока.

Аналогично матрица возводится в пятую и более высокие степени. Из практического опыта могу сказать, что иногда попадаются примеры на возведение в 4-ю степень, а вот уже пятой степени что-то не припомню. Но на всякий случай приведу оптимальный алгоритм:

1) находим ;
2) находим ;
3) возводим матрицу в пятую степень: .

Вот, пожалуй, и все основные свойства матричных операций, которые могут пригодиться в практических задачах.

Во втором разделе урока ожидается не менее пёстрая тусовка.

Матричные выражения

Повторим обычные школьные выражения с числами. Числовое выражение состоит из чисел, знаков математических действий и скобок, например: . При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки, затем выполняется возведение в степень / извлечение корней, потом умножение / деление и в последнюю очередь – сложение /вычитание.

Если числовое выражение имеет смысл, то результат его вычисления является числом, например:

Матричные выражения устроены практически так же! С тем отличием, что главными действующими лицами выступают матрицы. Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.

Рассмотрим матричное выражение , где  – некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь.

В первом слагаемом  сначала нужно транспонировать матрицу «бэ»: , потом выполнить умножение  и внести «двойку» в полученную матрицу. Обратите внимание, что операция транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий:  – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2.

Во втором слагаемом  в первую очередь выполняется матричное умножение , и обратная матрица находится уже от произведения. Если скобки убрать: , то сначала необходимо найти обратную матрицу , а затем перемножить матрицы: . Нахождение обратной матрицы также имеет приоритет перед умножением.

С третьим слагаемым  всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу.

Если матричное выражение имеет смысл, то результат его вычисления является матрицей.

Все задания будут из реальных контрольных работ, и мы начнём с самого простого:

Пример 9

Даны матрицы 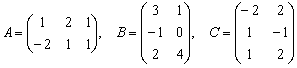. Найти:

Решение: порядок действий очевиден, сначала выполняется умножение, затем сложение.

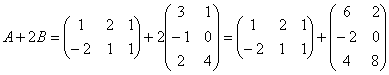
Сложение выполнить невозможно, поскольку матрицы разных размеров.

Не удивляйтесь, заведомо невозможные действия часто предлагаются в заданиях данного типа.

Пробуем вычислить второе выражение:

Тут всё нормально.

Ответ: действие  выполнить невозможно, .

Повысим градус:

Пример 10

Даны матрицы .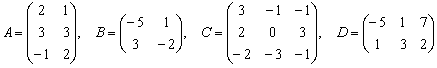

Найти значения выражений:

Решение: Разбираемся с произведением . Сначала транспонируем матрицы «дэ»:

И умножаем матрицы:

Матричное умножение выполнить невозможно, так как число столбцов матрицы  не равно числу строк матрицы .

А вот с произведением  проблем не возникает:

Еще раз заметьте, как на первом же шаге множитель (–1) выносится вперёд, и ноги до него доходят в самую последнюю очередь.

С более сложными выражениями вроде  чайникам рекомендую разбираться поэтапно, чтобы не запутаться:

Сначала находим произведение:

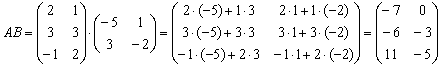
Затем считаем второе слагаемое:

И, наконец, всё выражение:

Более подготовленные студенты могут оформить решение одной строкой:

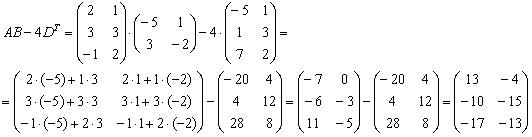
Ответ: действие  выполнить невозможно,  , .

Пара заключительных примеров для самостоятельного решения:

Пример 11

Для матриц Примера №10 выполнить действия:

Пример 12

Вычислить значение матричного многочлена , если .

В последнем примере решение удобно оформить по пунктам.

Матричные выражения – это просто! И вряд ли на практике вам встретится что-то сложнее, чем разобранные примеры.

Теперь во всеоружии можно приступить к изучению матричных уравнений.

Желаю успехов!

Решения и ответы:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте