


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Гипербола и парабола
Переходим ко второй части статьи о линиях второго порядка, посвященной двум другим распространённым кривым – гиперболе и параболе. Если вы зашли на данную страницу с поисковика либо ещё не успели сориентироваться в теме, то рекомендую сначала изучить первый раздел урока, на котором мы рассмотрели не только основные теоретические моменты, но и познакомились с эллипсом. Остальным же читателям предлагаю существенно пополнить свои школьные знания о параболе и гиперболе. Гипербола и парабола – это просто? …Не дождётесь =)
Гипербола и её каноническое уравнение
Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.
Каноническое уравнение гиперболы имеет вид ![]() , где
, где ![]() – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие
– положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие ![]() , то есть значение «а» может быть и меньше значения «бэ».
, то есть значение «а» может быть и меньше значения «бэ».
Надо сказать, довольно неожиданно… уравнение «школьной» гиперболы ![]() и близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока почешем затылок и вспомним, какими характерными особенностями обладает рассматриваемая кривая? Раскинем на экране своего воображения график функции
и близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока почешем затылок и вспомним, какими характерными особенностями обладает рассматриваемая кривая? Раскинем на экране своего воображения график функции ![]() ….
….
У гиперболы две симметричные ветви.
У гиперболы две асимптоты.
Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас мы с неподдельным восхищением заглянем в декольте этой линии:
Пример 4
Построить гиперболу, заданную уравнением ![]()
Решение: на первом шаге приведём данное уравнение к каноническому виду ![]() . Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому обе части исходного уравнения делим на 20:
. Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому обе части исходного уравнения делим на 20:

Здесь можно сократить обе дроби, но оптимальнее сделать каждую из них трёхэтажной:

И только после этого провести сокращение:
![]()
Выделяем квадраты в знаменателях:
![]()
Готово.
Почему преобразования лучше проводить именно так? Ведь дроби левой части ![]() можно сразу сократить и получить
можно сразу сократить и получить ![]() . Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае такой номер не проходит. Рассмотрим, например, уравнение
. Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае такой номер не проходит. Рассмотрим, например, уравнение ![]() . Здесь с делимостью всё печальнее и без трёхэтажных дробей уже не обойтись:
. Здесь с делимостью всё печальнее и без трёхэтажных дробей уже не обойтись:

Итак, воспользуемся плодом наших трудов – каноническим уравнением ![]() :
:
Как построить гиперболу?
Существует два подхода к построению гиперболы – геометрический и алгебраический.
С практической точки зрения вычерчивание с помощью циркуля... я бы даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.
Целесообразно придерживаться следующего алгоритма, сначала готовый чертёж, потом комментарии:

1) Прежде всего, находим асимптоты. Если гипербола задана каноническим уравнением ![]() , то её асимптотами являются прямые
, то её асимптотами являются прямые ![]() . В нашем случае:
. В нашем случае: ![]() . Данный пункт обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.
. Данный пункт обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.
2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках ![]() . Выводится элементарно: если
. Выводится элементарно: если ![]() , то каноническое уравнение
, то каноническое уравнение ![]() превращается в
превращается в ![]() , откуда и следует, что
, откуда и следует, что ![]() . Рассматриваемая гипербола имеет вершины
. Рассматриваемая гипербола имеет вершины ![]()
3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения ![]() на черновике выражаем:
на черновике выражаем:

Уравнение распадается на две функции:
![]() – определяет верхние дуги гиперболы (то, что нам надо);
– определяет верхние дуги гиперболы (то, что нам надо);
![]() – определяет нижние дуги гиперболы.
– определяет нижние дуги гиперболы.
Напрашивается нахождение точек с абсциссами ![]() :
:

4) Изобразим на чертеже асимптоты ![]() , вершины
, вершины ![]() , дополнительные
, дополнительные ![]() и симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
и симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
Техническая трудность может возникнуть с иррациональным угловым коэффициентом ![]() , но это вполне преодолимая проблема.
, но это вполне преодолимая проблема.
Отрезок ![]() называют действительной осью гиперболы,
называют действительной осью гиперболы,
его длину
![]() – расстоянием между вершинами;
– расстоянием между вершинами;
число ![]() называют действительной полуосью гиперболы;
называют действительной полуосью гиперболы;
число ![]() – мнимой полуосью.
– мнимой полуосью.
В нашем примере: ![]() , и, очевидно, если данную гиперболу повернуть вокруг центра симметрии и/или переместить, то эти значения не изменятся.
, и, очевидно, если данную гиперболу повернуть вокруг центра симметрии и/или переместить, то эти значения не изменятся.
Определение гиперболы. Фокусы и эксцентриситет
У гиперболы, точно так же, как и у эллипса, есть две особенные точки ![]() , которые называются фокусами. Не говорил, но на всякий случай, вдруг кто неверно понимает: центр симметрии и точки фокуса, разумеется, не принадлежат кривым.
, которые называются фокусами. Не говорил, но на всякий случай, вдруг кто неверно понимает: центр симметрии и точки фокуса, разумеется, не принадлежат кривым.
Общая концепция определения тоже похожа:
Гиперболой называют множество всех точек плоскости, абсолютное значение разности расстояний до каждой из которых от двух данных точек ![]() – есть величина постоянная, численно равная расстоянию между вершинами этой гиперболы:
– есть величина постоянная, численно равная расстоянию между вершинами этой гиперболы: ![]() . При этом расстояние между фокусами превосходит длину действительной оси:
. При этом расстояние между фокусами превосходит длину действительной оси: ![]() .
.
Если гипербола задана каноническим уравнением ![]() , то расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле:
, то расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: ![]() .
.
И, соответственно, фокусы имеют координаты ![]() .
.
Для исследуемой гиперболы ![]() :
:

Разбираемся в определении. Обозначим через ![]() расстояния от фокусов до произвольной точки
расстояния от фокусов до произвольной точки ![]() гиперболы:
гиперболы:
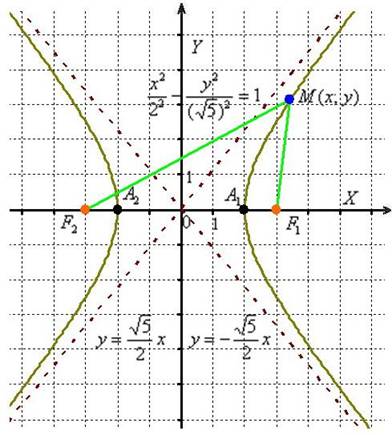
Сначала мысленно передвигайте синюю точку по правой ветви гиперболы – где бы мы ни находились, модуль (абсолютное значение) разности между длинами отрезков ![]() будет одним и тем же:
будет одним и тем же:
![]()
Если точку ![]() «перекинуть» на левую ветвь и перемещать её там, то данное значение останется неизменным.
«перекинуть» на левую ветвь и перемещать её там, то данное значение останется неизменным.
Знак модуля нужен по той причине, что разность длин ![]() может быть как положительной, так и отрицательной. Кстати, для любой точки правой ветви
может быть как положительной, так и отрицательной. Кстати, для любой точки правой ветви ![]() (поскольку отрезок
(поскольку отрезок ![]() короче отрезка
короче отрезка ![]() ). Для любой точки
). Для любой точки ![]() левой ветви ситуация ровно противоположная и
левой ветви ситуация ровно противоположная и ![]() .
.
Более того, ввиду очевидного свойства модуля ![]() безразлично, что из чего вычитать.
безразлично, что из чего вычитать.
Удостоверимся, что в нашем примере модуль данной разности действительно равен расстоянию между вершинами. Мысленно поместите точку![]() в правую вершину гиперболы
в правую вершину гиперболы ![]() . Тогда:
. Тогда: ![]() , что и требовалось проверить.
, что и требовалось проверить.
Эксцентриситетом гиперболы называют отношение ![]() .
.
Так как расстояние от центра до фокуса больше расстояния от центра до вершины: ![]() , то эксцентриситет гиперболы всегда больше «единицы»:
, то эксцентриситет гиперболы всегда больше «единицы»: ![]() .
.
Для данного примера: ![]() .
.
По аналогии с эллипсом, зафиксировав значение ![]() , желающие могут провести самостоятельный анализ и проверку следующих фактов:
, желающие могут провести самостоятельный анализ и проверку следующих фактов:
При увеличении эксцентриситета ветви гиперболы «распрямляются» к оси ![]() .
.
В предельном случае ![]() они стремятся занять положение двух прямых, проходящих через точки
они стремятся занять положение двух прямых, проходящих через точки ![]() параллельно оси ординат.
параллельно оси ординат.
Если же значение эксцентриситета приближается к единице, то ветви гиперболы «сплющиваются» к оси ![]() .
.
Равносторонняя гипербола
На практике часто встречается гипербола с равными полуосями. Если ![]() , то каноническое уравнение
, то каноническое уравнение ![]() заметно упрощается:
заметно упрощается:
![]()
А вместе с ним упрощаются и уравнения асимптот:

Прямые ![]() пересекаются под прямым углом и «справедливо» делят координатную плоскость на 4 одинаковые части, в двух из которых находятся ветви кривой. Образно говоря, равносторонняя гипербола «идеально сложена», то есть и не растянута и не сплющена.
пересекаются под прямым углом и «справедливо» делят координатную плоскость на 4 одинаковые части, в двух из которых находятся ветви кривой. Образно говоря, равносторонняя гипербола «идеально сложена», то есть и не растянута и не сплющена.
Так как ![]() , то
, то ![]() , следовательно, эксцентриситет любой равносторонней гиперболы равен:
, следовательно, эксцентриситет любой равносторонней гиперболы равен: ![]() .
.
Предлагаю закрепить теорию и практические навыки миниатюрной задачей:
Пример 5
Построить гиперболу ![]() и найти её фокусы.
и найти её фокусы.
Это пример для самостоятельного решения. Кто пропустит, тот пропустит многое ;-) Решение и чертёж в конце урока.
Начнём тревожить беззаботное существование нашей кривой:
Поворот вокруг центра и параллельный перенос гиперболы
Вернёмся к демонстрационной гиперболе ![]() . Что произойдёт, если в полученном уравнении поменять значения полуосей:
. Что произойдёт, если в полученном уравнении поменять значения полуосей: ![]() ? Для эллипса данный трюк означал поворот на 90 градусов. Но здесь всё иначе! Уравнение
? Для эллипса данный трюк означал поворот на 90 градусов. Но здесь всё иначе! Уравнение ![]() определяет совершенно другую гиперболу. Ну, хотя бы обратите внимание на иные вершины:
определяет совершенно другую гиперболу. Ну, хотя бы обратите внимание на иные вершины: ![]() .
.
Теперь рассмотрим уравнение ![]() , которое очевидно тоже задаёт гиперболу. Однако к исходному уравнению оно также не имеет никакого отношения! Это предыдущая гипербола, повёрнутая на 90 градусов, с вершинами
, которое очевидно тоже задаёт гиперболу. Однако к исходному уравнению оно также не имеет никакого отношения! Это предыдущая гипербола, повёрнутая на 90 градусов, с вершинами ![]() на оси ординат.
на оси ординат.
И, наконец, оставшийся случай ![]() задаёт нашу гиперболу
задаёт нашу гиперболу ![]() , повернутую на 90 градусов. Как быть, если в практической задаче встретилась такая неканоническая запись?
, повернутую на 90 градусов. Как быть, если в практической задаче встретилась такая неканоническая запись?
Если требуется только построить кривую, то строим её в предложенном виде. Это довольно просто. Уравнения асимптот гиперболы ![]() обладают обратными угловыми коэффициентами:
обладают обратными угловыми коэффициентами:
![]()
Поскольку оси «поменялись ролями», то вершины будут расположены на оси ординат в точках ![]() . Выразим верхнюю ветвь гиперболы:
. Выразим верхнюю ветвь гиперболы:

И найдём несколько дополнительных точек:

Выполним чертёж:
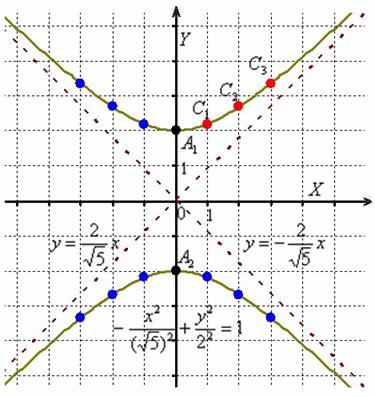
Помимо геометрии, похожие графики требуется строить в некоторых задачах математического анализа.
Однако по возможности всё-таки лучше осуществить поворот на 90 градусов и переписать уравнение ![]() в канонической форме. Для этого следует поменять местами значения полуосей и переставить «минус» к переменной «игрек»:
в канонической форме. Для этого следует поменять местами значения полуосей и переставить «минус» к переменной «игрек»: ![]() .
.
И далее работать уже с каноническим уравнением.
! Примечание: строгий теоретический подход предполагает поворот координатных осей, а не самой линии. При необходимости оформляйте решение по аналогии с соответствующим примечанием предыдущего урока.
Параллельный перенос. Уравнение ![]() задаёт гиперболу с действительной полуосью «а», мнимой полуосью «бэ» и центром в точке
задаёт гиперболу с действительной полуосью «а», мнимой полуосью «бэ» и центром в точке ![]() .
.
Так, например, гипербола ![]() имеет центр симметрии в точке
имеет центр симметрии в точке ![]() . Асимптоты, само собой, переместились вместе с гиперболой, их уравнения отыскиваются по формулам:
. Асимптоты, само собой, переместились вместе с гиперболой, их уравнения отыскиваются по формулам:

Полуоси ![]() и расстояние от фокусов до центра симметрии
и расстояние от фокусов до центра симметрии ![]() остались прежними, а вот координаты фокусов изменились с учётом параллельного переноса:
остались прежними, а вот координаты фокусов изменились с учётом параллельного переноса:

Параллельный перенос гиперболы доставил заметно больше хлопот, чем параллельный перенос эллипса, смотрим на картинку:
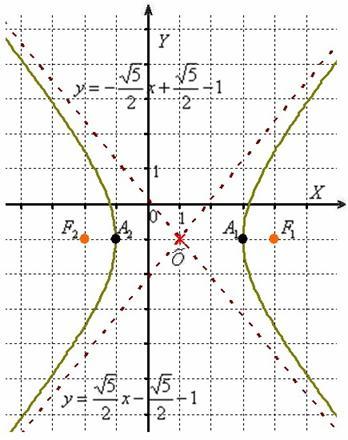
После таких трудов, уравнение трогать бессмысленно, но если таки просят, то придётся….
В нестрогом варианте: «Приведём уравнение гиперболы ![]() к каноническому виду путём параллельного переноса в начало координат:
к каноническому виду путём параллельного переноса в начало координат: ![]() ».
».
Или в строгом – с параллельным переносом системы координат началом в точку ![]()
(см. шаблон у эллипса).
На практике часто встречается комбинация поворота на произвольный угол и параллельного переноса гиперболы. Данная ситуация рассматривается на уроке Приведение уравнения линии 2-го порядка к каноническому виду.
Парабола и её каноническое уравнение
Свершилось! Она самая. Готовая раскрыть немало тайн. Каноническое уравнение параболы имеет вид ![]() , где
, где ![]() – действительное число. Нетрудно заметить, что в своём стандартном положении парабола «лежит на боку» и её вершина находится в начале координат. При этом функция
– действительное число. Нетрудно заметить, что в своём стандартном положении парабола «лежит на боку» и её вершина находится в начале координат. При этом функция ![]() задаёт верхнюю ветвь данной линии, а функция
задаёт верхнюю ветвь данной линии, а функция ![]() – нижнюю ветвь. Очевидно, что парабола симметрична относительно оси
– нижнюю ветвь. Очевидно, что парабола симметрична относительно оси ![]() . Собственно, чего париться:
. Собственно, чего париться:
Пример 6
Построить параболу ![]()
Решение: вершина известна, найдём дополнительные точки. Уравнение ![]() определяет верхнюю дугу параболы, уравнение
определяет верхнюю дугу параболы, уравнение ![]() – нижнюю дугу.
– нижнюю дугу.
В целях сократить запись вычисления проведём «под одной гребёнкой» ![]() :
:

Для компактной записи результаты можно было свести в таблицу.
Перед тем, как выполнить элементарный поточечный чертёж, сформулируем строгое
определение параболы:
Параболой называется множество всех точек плоскости, равноудалённых от данной точки ![]() и данной прямой
и данной прямой ![]() , не проходящей через точку
, не проходящей через точку ![]() .
.
Точка ![]() называется фокусом параболы, прямая
называется фокусом параболы, прямая ![]() – директрисой (пишется с одной «эс») параболы. Константа «пэ» канонического уравнения
– директрисой (пишется с одной «эс») параболы. Константа «пэ» канонического уравнения ![]() называется фокальным параметром, который равен расстоянию от фокуса до директрисы. В данном случае
называется фокальным параметром, который равен расстоянию от фокуса до директрисы. В данном случае ![]() . При этом фокус имеет координаты
. При этом фокус имеет координаты ![]() , а директриса задаётся уравнением
, а директриса задаётся уравнением ![]() .
.
В нашем примере ![]() :
:
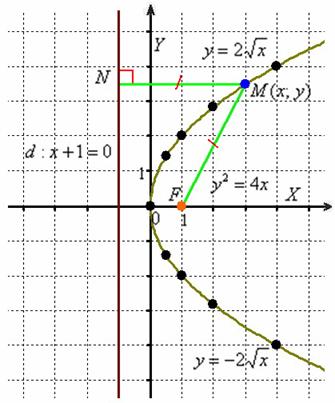
Определение параболы понимается ещё проще, чем определения эллипса и гиперболы. Для любой точки ![]() параболы длина отрезка
параболы длина отрезка ![]() (расстояние от фокуса до точки) равна длине перпендикуляра
(расстояние от фокуса до точки) равна длине перпендикуляра ![]() (расстоянию от точки до директрисы):
(расстоянию от точки до директрисы):
![]()
Поздравляю! Многие из вас сегодня сделали самое настоящее открытие. Оказывается, гипербола и парабола вовсе не являются графиками «рядовых» функций, а имеют ярко выраженное геометрическое происхождение.
Очевидно, что при увеличении фокального параметра ветви графика ![]() будут «раздаваться» вверх и вниз, бесконечно близко приближаясь к оси
будут «раздаваться» вверх и вниз, бесконечно близко приближаясь к оси ![]() . При уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси
. При уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси ![]()
Эксцентриситет любой параболы равен единице: ![]()
Поворот и параллельный перенос параболы
Парабола – одна из самых распространённых линий в математике, и строить её придётся действительно часто. Поэтому, пожалуйста, особенно внимательно отнестись к заключительному параграфу урока, где я разберу типовые варианты расположения данной кривой.
! Примечание: как и в случаях с предыдущими кривыми, корректнее говорить о повороте и параллельном переносе координатных осей, но автор ограничится упрощённым вариантом изложения, чтобы у читателя сложились элементарные представления о данных преобразованиях.
1) Поворот вокруг вершины. Если в уравнении присутствует знак «минус»: ![]() , то это означает разворот параболы на 180 градусов относительно своего канонического положения. А если в уравнении
, то это означает разворот параболы на 180 градусов относительно своего канонического положения. А если в уравнении ![]() переменные «поменялись местами»:
переменные «поменялись местами»: ![]() , то это означает поворот канонической параболы на 90 градусов против часовой стрелки.
, то это означает поворот канонической параболы на 90 градусов против часовой стрелки.
На следующем чертеже изображены графики кривых ![]() :
:
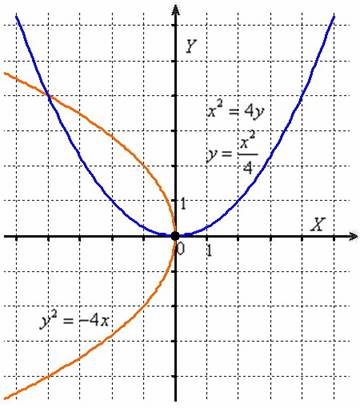
Оба уравнения задают неканоническое расположение нашей подопытной параболы ![]() , причём во втором случае легко получить функциональную запись, к которой мы привыкли в курсе математического анализа:
, причём во втором случае легко получить функциональную запись, к которой мы привыкли в курсе математического анализа: ![]() .
.
Таким образом, все параболы, с которыми мы обычно работаем – не каноничны! Я очень хотел «уложить на бок» классическую параболу ![]() и разобрать каноническое уравнение
и разобрать каноническое уравнение ![]() , но, к сожалению, у неё достаточно малый фокальный параметр
, но, к сожалению, у неё достаточно малый фокальный параметр ![]() , и чертеж с точкой фокуса
, и чертеж с точкой фокуса ![]() , директрисой
, директрисой ![]() был бы крайне невразумителен.
был бы крайне невразумителен.
2) Параллельный перенос. Без всякой оригинальности. Уравнение ![]() задаёт ту же параболу
задаёт ту же параболу ![]() с вершиной в точке
с вершиной в точке ![]() . По моим наблюдениям, во многих задачах матана очень популярен частный случай
. По моим наблюдениям, во многих задачах матана очень популярен частный случай ![]() – когда каноническая парабола сдвигается влево или вправо по оси абсцисс. Ну, и как дополнительная опция, разворачивается, если при переменной «икс» есть знак «минус».
– когда каноническая парабола сдвигается влево или вправо по оси абсцисс. Ну, и как дополнительная опция, разворачивается, если при переменной «икс» есть знак «минус».
Соответствующее творческое задание для самостоятельного решения:
Пример 7
Построить параболу ![]() . Привести уравнение линии к каноническому виду, найти фокус и уравнение директрисы.
. Привести уравнение линии к каноническому виду, найти фокус и уравнение директрисы.
Как лучше действовать?
По условию требуется построить параболу ![]() . Именно такую – в неканоническом виде! Поэтому в первой части задачи следует представить уравнение в виде
. Именно такую – в неканоническом виде! Поэтому в первой части задачи следует представить уравнение в виде ![]() , что позволит сразу определить вершину. Затем по образцу Примера 6 нужно провести поточечное построение линии, работая с уравнениями
, что позволит сразу определить вершину. Затем по образцу Примера 6 нужно провести поточечное построение линии, работая с уравнениями ![]() .
.
Вторая часть задания предполагает приведение уравнения к каноническому виду. Проанализируйте равенство ![]() – есть ли поворот, есть ли параллельный перенос? После того, как выясните каноническую запись
– есть ли поворот, есть ли параллельный перенос? После того, как выясните каноническую запись ![]() , необходимо найти фокус параболы и уравнение её директрисы. Обратите внимание, что в контексте условия это, вероятнее всего, нужно сделать в каноническом положении!
, необходимо найти фокус параболы и уравнение её директрисы. Обратите внимание, что в контексте условия это, вероятнее всего, нужно сделать в каноническом положении!
Ну, а наша обзорная экскурсия подошла к концу, и я надеюсь, что у вас не возникло и не возникнет трудностей с тремя атлантами темы – эллипсом, гиперболой и параболой. Предлагаю узнать новый теоретический материал и закрепить практические навыки на уроке Задачи с линиями 2-го порядка.
Желаю успехов!
Решения и чертежи:
Пример 5. Решение: данная гипербола является равносторонней, поэтому имеет асимптоты ![]() . Действительная полуось
. Действительная полуось ![]() , значит, вершины расположены в точках
, значит, вершины расположены в точках ![]() . Найдём дополнительные точки:
. Найдём дополнительные точки:

Определим координаты фокусов: ![]()
![]()
Выполним чертёж:
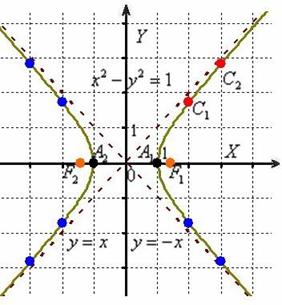
Перед вами «школьная» гипербола в каноническом положении. График функции ![]() получается путём поворота (вокруг начала координат) построенного графика
получается путём поворота (вокруг начала координат) построенного графика ![]() на 45 градусов против часовой стрелки (а если строже – путём поворота системы координат на противоположно ориентированный угол в «минус» 45 градусов).
на 45 градусов против часовой стрелки (а если строже – путём поворота системы координат на противоположно ориентированный угол в «минус» 45 градусов).
И в общем случае – график обратной пропорциональности ![]() представляет собой равностороннюю гиперболу, уравнение которой можно привести к каноническому виду
представляет собой равностороннюю гиперболу, уравнение которой можно привести к каноническому виду ![]() .
.
Пример 7. Решение: преобразуем уравнение:
![]()
Вершина параболы находится в точке ![]() , ветви направлены влево. С помощью уравнений
, ветви направлены влево. С помощью уравнений  найдём дополнительные точки:
найдём дополнительные точки:

Выполним чертёж:
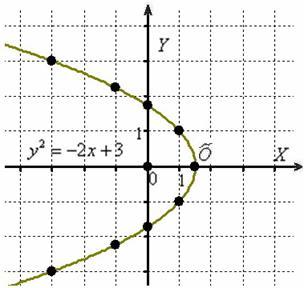
Парабола ![]() получена путём поворота параболы
получена путём поворота параболы ![]() на 180 градусов и её параллельного переноса в точку
на 180 градусов и её параллельного переноса в точку ![]() . Из канонического уравнения
. Из канонического уравнения ![]() находим фокальный параметр
находим фокальный параметр ![]() , фокус
, фокус ![]() и уравнение директрисы
и уравнение директрисы ![]() .
.
Примечание: в случае необходимости нетрудно найти координаты фокуса и уравнение директрисы неканонически расположенной параболы ![]() . Учитывая поворот и параллельный перенос:
. Учитывая поворот и параллельный перенос: ![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright