Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Метод касательных

Метод касательных (метод Ньютона) предназначен для приближенного нахождения нулей функции, и сегодня мы не только узнаем его суть, но и научимся быстро решать тематическую задачу! В которой чаще всего фигурирует «обычная» функция одной переменной  и соответствующее уравнение . Например:

Поставим задачу отыскать действительные корни данного уравнения.

А таковые точно есть! – из статей о графиках функций и уравнениях высшей математики вы хорошо знаете, что график функции-многочлена  нечётной степени хотя бы один раз пересекает ось , следовательно, наше уравнение имеет по меньшей мере один действительный корень. Один. Или два. Или три.

Сначала напрашивается проверить, наличие рациональных корней. Согласно соответствующей теореме, на это «звание» могут претендовать лишь числа 1, –1, 3, –3, и прямой подстановкой легко убедиться, что ни одно из них «не подходит». Таким образом, остаются иррациональные значения. Иррациональный корень (корни) многочлена 3-й степени можно найти точно (выразить через радикалы) с помощью так называемых формул Кардано, однако этот метод достаточно громоздок. А для многочленов 5-й и бОльших степеней общего аналитического метода не существует вовсе, и, кроме того, на практике встречается множество других уравнений, в которых точные значения действительных корней получить невозможно (хотя они существуют).

Однако в прикладных (например, инженерных) задачах более чем допустимо использовать приближённые значения, вычисленные с определённой точностью.

Зададим для нашего примера точность . Что это значит? Это значит, что нам нужно отыскать ТАКОЕ приближённое значение корня  (корней), в котором мы гарантированно ошибаемся, не более чем на 0,001 (одну тысячную).

Совершенно понятно, что решение нельзя начинать «наобум» и поэтому на первом шаге корни отделяют. Отделить корень – это значит найти достаточно малый (как правило, единичный) отрезок, которому этот корень принадлежит, и на котором нет других корней. Наиболее прост и доступен графический метод отделения корней. Построим поточечно график функции :

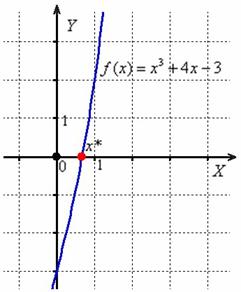
Из чертежа следует, что уравнение , судя по всему, имеет единственный действительный корень , принадлежащий отрезку . На концах данного промежутка функция  принимает значения разных знаков: , и из факта непрерывности функции на отрезке сразу виден элементарный способ уточнения корня: делим промежуток  пополам  и выбираем тот отрезок, на концах которого функция принимает разные знаки. В данном случае это, очевидно, отрезок . Делим полученный промежуток пополам и снова выбираем «разнознаковый» отрезок. И так далее. Подобные последовательные действия называют итерациями.  В данном случае их следует проводить до тех пор, пока длина отрезка не станет меньше удвоенной точности вычислений , и за приближённое значение корня следует выбрать середину последнего «разнознакового» отрезка. 

Рассмотренная схема получила естественное название – метод половинного деления. И недостаток этого метода состоит в скорости. Медленно. Очень медленно. Слишком много итераций придётся совершить, прежде чем мы достигнем требуемой точности. С развитием вычислительной техники это, конечно, не проблема, но математика – на то и математика, чтобы искать наиболее рациональные пути решения.

И одним из более эффективных способов нахождения приближённого значения корня как раз и является метод касательных. Краткая геометрическая суть метода состоит в следующем: сначала с помощью специального критерия (о котором чуть позже) выбирается один из концов отрезка. Этот конец называют начальным приближением корня, в нашем примере: . Теперь проводим касательную к графику функции  в точке с абсциссой  (синяя точка и фиолетовая касательная):

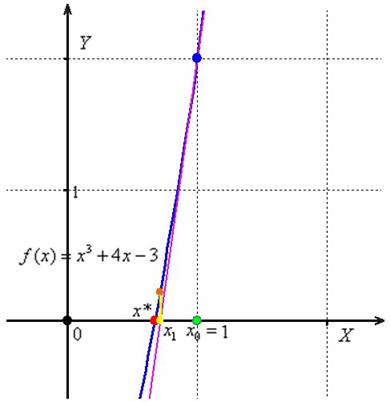
Данная касательная пересекла ось абсцисс в жёлтой точке, и обратите внимание, что на первом шаге мы уже почти «попали в корень»! Это будет первое приближение корня . Далее опускаем жёлтый перпендикуляр к графику функции и «попадаем» в оранжевую точку. Через оранжевую точку снова проводим касательную, которая пересечёт ось ещё ближе к корню! И так далее. Нетрудно понять, что, используя метод касательных, мы приближаемся к цели семимильными шагами, и для достижения точности  потребуется буквально несколько итераций.

Поскольку касательная определяется через производную функции, то этот урок попал в раздел «Производные» в качестве одного из её приложений. И, не вдаваясь в подробное теоретическое обоснование метода, я рассмотрю техническую сторону вопроса. На практике описанная выше задача встречается примерно в такой формулировке:

Пример 1

С помощью графического метода найти промежуток , на котором находится действительный корень  уравнения . Пользуясь методом Ньютона, получить приближенное значение корня с точностью до 0,001

Перед вами «щадящая версия» задания, в которой сразу констатируется наличие единственного действительного корня.

Решение: на первом шаге следует отделить корень графически. Это можно сделать путём построения графика  (см. иллюстрации выше), но такой подход обладает рядом недостатков. Во-первых, не факт, что график прост (мы же заранее не знаем), а программное обеспечение – оно далеко не всегда под рукой. И, во-вторых (следствие из 1-го), с немалой вероятностью получится даже не схематичный чертёж, а грубый рисунок, что, разумеется, не есть хорошо.

Ну а зачем нам лишние трудности? Представим уравнение  в виде , АККУРАТНО построим графики  и отметим на чертеже корень  («иксовую» координату точки пересечения графиков):

Очевидное преимущество этого способа состоит в том, что графики данных функций строятся от руки значительно точнее и намного быстрее. Кстати, заметьте, что прямая пересекла кубическую параболу в единственной точке, а значит, предложенное уравнение и в самом деле имеет только один действительный корень. Доверяйте, но проверяйте ;-)   

Итак, наш «клиент»  принадлежит отрезку  и «на глазок» примерно равен 0,65-0,7.

На втором шаге нужно выбрать начальное приближение  корня. Обычно это один из концов отрезка. Начальное приближение должно удовлетворять следующему условию:

Найдём первую и вторую производные функции :

и проверим левый конец отрезка:

Таким образом, ноль «не подошёл».

Проверяем правый конец отрезка:

 – всё хорошо!  В качестве начального приближения выбираем .

На третьем шаге нас ожидает дорога к корню. Каждое последующее приближение  корня  рассчитывается на основании предшествующих данных с помощью следующей рекуррентной формулы:

Процесс завершается при выполнении условия , где  – заранее заданная точность вычислений. В результате за приближённое значение корня принимается «энное» приближение: .

На очереди рутинные расчёты:

 (округление обычно проводят до 5-6 знаков после запятой)

Поскольку полученное значение больше , то переходим к 1-му приближению корня:

Вычисляем:

, поэтому возникает потребность перейти ко 2-му приближению:

Заходим на следующий круг:

, таким образом, итерации закончены, и в качестве приближённого значения корня следует взять 2-е приближение, которое в соответствии с заданной точностью нужно округлить до одной тысячной:

На практике результаты вычислений удобно заносить в таблицу, при этом, чтобы несколько сократить запись, дробь часто обозначают через :

Сами же вычисления по возможности лучше провести в Экселе – это намного удобнее и быстрее:

Ответ:  с точностью до 0,001

Напоминаю, что эта фраза подразумевает тот факт, что мы ошиблись в оценке истинного значения корня не более чем на 0,001. Сомневающиеся могут взять в руки микрокалькулятор и ещё раз подставить приближенное значение 0,674 в левую часть уравнения .

А теперь «просканируем» правый столбец таблицы сверху вниз и обратим внимание, что значения  неуклонно убывают по модулю. Этот эффект называют сходимостью метода, которая позволяет нам вычислить корень со сколь угодно высокой точностью. Но сходимость имеет место далеко не всегда – она обеспечивается рядом условий, о которых я умолчал. В частности, отрезок, на котором изолируется корень, должен быть достаточно мал – в противном случае значения  будут меняться беспорядочным образом, и мы не сможем завершить алгоритм.

Что делать в таких случаях? Проверить выполнение указанных условий (см. выше по ссылке), и при необходимости уменьшить отрезок. Так, условно говоря, если бы в разобранном примере нам не подошёл промежуток , то следовало бы рассмотреть, например, отрезок . На практике мне такие случаи встречались, и этот приём реально помогает! То же самое нужно сделать, если оба конца «широкого» отрезка не удовлетворяют условию (т.е. ни один из них не годится на роль начального приближения).

Но обычно всё работает, как часы, хотя и не без подводных камней:

Пример 2

Определить графически количество действительных корней уравнения  , отделить эти корни и применяя способ Ньютона, найти приближенные значения корней с точностью

Условие задачи заметно ужесточилось: во-первых, в нём содержится толстый намёк на то, что уравнение имеет не единственный  корень, во-вторых, повысилось требование к точности, и, в-третьих, с графиком функции  совладать значительно труднее.

А поэтому решение начинаем со спасительного трюка: представим уравнение в виде   и изобразим графики :

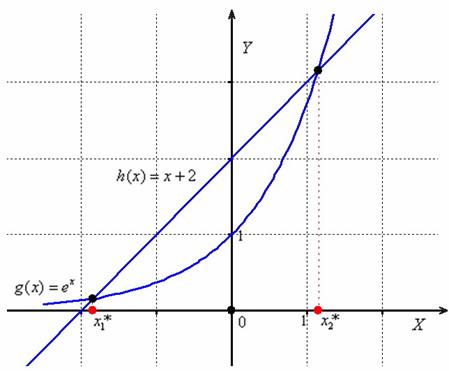
Из чертежа следует, что наше уравнение имеет два действительных корня:

Алгоритм, как вы понимаете, нужно «провернуть» дважды. Но это ещё не самый тяжелый случай, бывает, исследовать приходится 3-4 корня.

1) С помощью критерия  выясним, какой из концов отрезка  выбрать в качестве начального приближения первого корня. Находим производные функции :

Тестируем левый конец отрезка:

 – подошёл!

Таким образом,  – начальное приближение.

Уточнение корня проведем методом Ньютона, используя рекуррентную формулу:
 – до тех пор, пока дробь по модулю не станет меньше требуемой точности:

И здесь слово «модуль» приобретает неиллюзорную важность, поскольку значения  получаются отрицательными:

По этой же причине следует проявить повышенное внимание при переходе к каждому следующему приближению:

Несмотря на достаточно высокое требование к точности, процесс опять завершился на 2-м приближении: , следовательно:

 с точностью до 0,0001

2) Найдем приближённое значение корня .

Проверяем на «вшивость» левый конец отрезка:

, следовательно, он не годится в качестве начального приближения.

«Прозваниваем» правый конец:

Таким образом:  – начальное приближение.

Вычисления сведём в таблицу:

Здесь пришлось немножко постараться, правда, если выполнять вычисления в Экселе, то все «старания» займут доли секунды =)

, следовательно, итерации закончены:

Ответ: уравнение имеет два действительных корня:  с точностью до 0,001

Парочка примеров для самостоятельного решения. И даже не столько для решения, сколько для отработки техники вычислений – сам-то алгоритм весьма примитивен:

Пример 3

Отделить действительный корень уравнения  графически, и вычислить его приближенное значение методом касательных с точностью до 0,001

Пример 4

Определить количество действительных корней уравнения , отделить эти корни и применяя способ Ньютона, найти приближенные значения корней с точностью

Заметьте, что в последнем задании явно не указано, каким способом мы должны изолировать корни, и, в принципе, можно попробовать обойтись чисто аналитическими выкладками, за которые по идее не должны покарать. Другое дело, что графический метод почти всегда проще.

Пожалуй, основные практически важные моменты я раскрыл, а посему статья плавно перетекает в решения и ответы, где можно ознакомиться с примерными образцами чистового оформления рассмотренной задачи:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте