


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить площадь поверхности вращения?
Рад приветствовать вас на «окраине» темы, где мы разберём ещё одно, более редкое приложение определённого интеграла – нахождение площади поверхности вращения. Предполагаю, что здесь собрались люди, знающие толк в интегралах, поэтому сразу перейду к основным понятиям и практическим примерам.
Посмотрим на лаконичную картинку
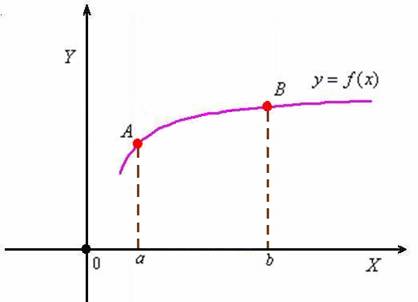
и вспомним: что можно вычислить с помощью определённого интеграла?
В первую очередь, конечно, площадь криволинейной трапеции. Знакомо со школьных времён.
Если же данная фигура вращается вокруг координатной оси, то речь уже идёт о нахождении объёма тела вращения. Тоже просто.
Что ещё? Не так давно была рассмотрена задача о длине дуги кривой ![]() .
.
И сегодня мы научимся рассчитывать ещё одну характеристику – ещё одну площадь. Представьте, что линия ![]() вращается вокруг оси
вращается вокруг оси ![]() . В результате этого действия получается геометрическая фигура, называемая поверхностью вращения. В данном случае она напоминает такой горшок без дна. И без крышки. Как бы сказал ослик Иа-Иа, душераздирающее зрелище =)
. В результате этого действия получается геометрическая фигура, называемая поверхностью вращения. В данном случае она напоминает такой горшок без дна. И без крышки. Как бы сказал ослик Иа-Иа, душераздирающее зрелище =)
Чтобы исключить двусмысленную трактовку, сделаю занудное, но важное уточнение:
с геометрической точки зрения наш «горшок» имеет бесконечно тонкую стенку и две поверхности с одинаковыми площадями – внешнюю и внутреннюю. Так вот, все дальнейшие выкладки подразумевают площадь только внешней поверхности.
В прямоугольной системе координат площадь поверхности вращения рассчитывается по формуле:
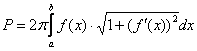 или, если компактнее:
или, если компактнее:  .
.
К функции и её производной предъявляются те же требования, что и при нахождении длины дуги кривой, но, кроме того, кривая ![]() должна располагаться выше оси
должна располагаться выше оси ![]() . Это существенно! Нетрудно понять, что если линия располагается под осью
. Это существенно! Нетрудно понять, что если линия располагается под осью ![]() , то подынтегральная функция будет отрицательной:
, то подынтегральная функция будет отрицательной: ![]() , и поэтому к формуле придётся добавить знак «минус» дабы сохранить геометрический смысл задачи.
, и поэтому к формуле придётся добавить знак «минус» дабы сохранить геометрический смысл задачи.
Рассмотрим незаслуженно обойденную вниманием фигуру:
Площадь поверхности тора
В двух словах, тор – это бублик. Хрестоматийный пример, рассматриваемый практически во всех учебниках по матану, посвящён нахождению объёма тора, и поэтому в целях разнообразия я разберу более редкую задачу о площади его поверхности. Сначала с конкретными числовыми значениями:
Пример 1
Вычислить площадь поверхности тора, полученного вращением окружности ![]() вокруг оси
вокруг оси ![]() .
.
Решение: как вы знаете, уравнение ![]() задаёт окружность единичного радиуса с центром в точке
задаёт окружность единичного радиуса с центром в точке ![]() . При этом легко получить две функции:
. При этом легко получить две функции:
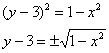
![]() – задаёт верхнюю полуокружность;
– задаёт верхнюю полуокружность;
![]() – задаёт нижнюю полуокружность:
– задаёт нижнюю полуокружность:
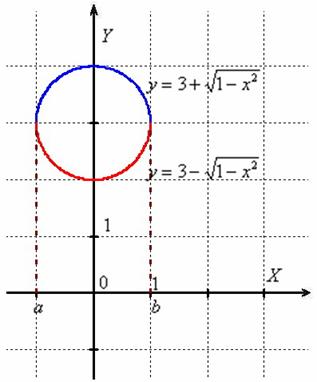
Суть кристально прозрачна: окружность вращается вокруг оси абсцисс и образует поверхность бублика. Единственное, здесь во избежание грубых оговорок следует проявить аккуратность в терминологии: если вращать круг, ограниченный окружностью ![]() , то получится геометрическое тело, то есть сам бублик. И сейчас разговор о площади его поверхности, которую, очевидно, нужно рассчитать как сумму площадей:
, то получится геометрическое тело, то есть сам бублик. И сейчас разговор о площади его поверхности, которую, очевидно, нужно рассчитать как сумму площадей:
1) Найдём площадь поверхности, которая получается вращением «синей» дуги ![]() вокруг оси абсцисс. Используем формулу
вокруг оси абсцисс. Используем формулу  . Как я уже неоднократно советовал, действия удобнее проводить поэтапно:
. Как я уже неоднократно советовал, действия удобнее проводить поэтапно:
Берём функцию ![]() и находим её производную:
и находим её производную:
![]()
Далее максимально упрощаем корень:

И, наконец, заряжаем результат в формулу:
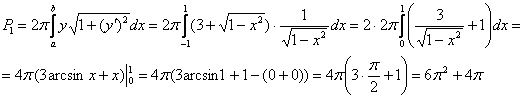
Заметьте, что в данном случае оказалось рациональнее удвоить интеграл от чётной функции по ходу решения, нежели предварительно рассуждать о симметрии фигуры относительно оси ординат.
2) Найдём площадь поверхности, которая получается вращением «красной» дуги ![]() вокруг оси абсцисс. Все действия будут отличаться фактически только одним знаком. Оформлю решение в другом стиле, который, само собой, тоже имеет право на жизнь:
вокруг оси абсцисс. Все действия будут отличаться фактически только одним знаком. Оформлю решение в другом стиле, который, само собой, тоже имеет право на жизнь:

3) Таким образом, площадь поверхности тора:
![]()
Ответ: ![]()
Задачу можно было решить в общем виде – вычислить площадь поверхности тора, полученного вращением окружности ![]() вокруг оси абсцисс, и получить ответ
вокруг оси абсцисс, и получить ответ ![]() . Однако для наглядности и бОльшей простоты я провёл решение на конкретных числах.
. Однако для наглядности и бОльшей простоты я провёл решение на конкретных числах.
Если вам необходимо рассчитать объём самого бублика, пожалуйста, обратитесь к учебнику, в качестве экспресс-справки: ![]()
Что только мы не делали с параболой за годы обучения, поэтому было бы большим упущением не покрутить её в своё удовольствие:
Пример 2
Вычислить площадь поверхности тела, полученного вращением параболы ![]() вокруг оси
вокруг оси ![]() на промежутке
на промежутке ![]() .
.
Здесь нужно рассмотреть верхнюю ветвь и действовать по стандартному алгоритму. Сама поверхность вращения, как многие представили, напоминает «кружку с яйцевидным дном», что кармически намного лучше дырявого горшка =)
Краткое решение и ответ в конце урока.
Чертёж в рассматриваемом типе задач не обязателен (кроме затейливых примеров), но всегда полезно хотя бы иметь представление о поверхности вращения.
Площадь поверхности вращения при параметрически заданной линии
Если кривая ![]() задана параметрическими уравнениями
задана параметрическими уравнениями ![]() , то площадь поверхности, полученной вращением данной кривой вокруг оси
, то площадь поверхности, полученной вращением данной кривой вокруг оси ![]() , рассчитывается по формуле
, рассчитывается по формуле 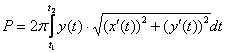 . При этом «направление прорисовки» линии, о которое было сломано столько копий в статье Площадь и объем, если линия задана параметрически, безразлично. Но, как и в предыдущем пункте, важно чтобы кривая располагалась выше оси абсцисс – в противном случае функция
. При этом «направление прорисовки» линии, о которое было сломано столько копий в статье Площадь и объем, если линия задана параметрически, безразлично. Но, как и в предыдущем пункте, важно чтобы кривая располагалась выше оси абсцисс – в противном случае функция ![]() , «отвечающая за игреки», будет принимать отрицательные значения и перед интегралом придётся поставить знак «минус».
, «отвечающая за игреки», будет принимать отрицательные значения и перед интегралом придётся поставить знак «минус».
Пример 3
Вычислить площадь сферы, полученной вращением окружности ![]() вокруг оси
вокруг оси ![]() .
.
Решение: из материалов статьи о площади и объемё при параметрически заданной линии вы знаете, что уравнения ![]() задают окружность с центром в начале координат радиуса 3.
задают окружность с центром в начале координат радиуса 3.
Ну а сфера, для тех, кто забыл, – это поверхность шара (или шаровая поверхность).
Придерживаемся наработанной схемы решения. Найдём производные:
![]()
Составим и упростим «формульный» корень:
![]()
Что и говорить, получилась конфетка. Ознакомьтесь для сравнения, как Фихтенгольц бодался с площадью эллипсоида вращения.
Согласно теоретической ремарке, рассматриваем верхнюю полуокружность. Она «прорисовывается» при изменении значения параметра в пределах ![]() (легко видеть, что
(легко видеть, что ![]() на данном промежутке), таким образом:
на данном промежутке), таким образом:
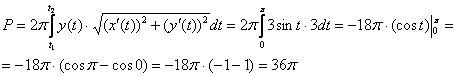
Ответ: ![]()
Если решить задачу в общем виде, то получится в точности школьная формула площади сферы ![]() , где
, где ![]() – её радиус.
– её радиус.
Что-то больно простая задачка, даже стыдно стало…. предлагаю вам исправить такую недоработку =)
Пример 4
Вычислить площадь поверхности, полученной вращением первой арки циклоиды ![]() вокруг оси
вокруг оси ![]() .
.
Задание креативное. Постарайтесь вывести или интуитивно догадаться о формуле вычисления площади поверхности, полученной вращением кривой вокруг оси ординат. И, конечно, снова следует отметить преимущество параметрических уравнений – их не нужно как-то видоизменять; не нужно заморачиваться с нахождением других пределов интегрирования.
График циклоиды можно посмотреть на странице Площадь и объем, если линия задана параметрически. Поверхность вращения будет напоминать… даже не знаю с чем сравнить… что-то неземное – округлой формы с остроконечным углублением посередине. Вот для случая вращения циклоиды вокруг оси ![]() ассоциация в голову мгновенно пришла – продолговатый мяч для игры в регби.
ассоциация в голову мгновенно пришла – продолговатый мяч для игры в регби.
Решение и ответ в конце урока.
Завершаем наш увлекательный обзор случаем полярных координат. Да, именно обзор, если вы заглянете в учебники по математическому анализу (Фихтенгольца, Бохана, Пискунова, др. авторов), то сможете раздобыть добрый десяток (а то и заметно больше) стандартных примеров, среди которых вполне возможно найдётся нужная вам задача.
Как вычислить площадь поверхности вращения,
если линия задана в полярной системе координат?
Если кривая задана в полярных координатах уравнением ![]() , и функция
, и функция ![]() имеет непрерывную производную
имеет непрерывную производную ![]() на данном промежутке, то площадь поверхности, полученной вращением данной кривой вокруг полярной оси, рассчитывается по формуле
на данном промежутке, то площадь поверхности, полученной вращением данной кривой вокруг полярной оси, рассчитывается по формуле  , где
, где ![]() – угловые значения, соответствующие концам кривой.
– угловые значения, соответствующие концам кривой.
В соответствии с геометрическим смыслом задачи подынтегральная функция ![]() , а это достигается только при условии
, а это достигается только при условии ![]() (
(![]() и
и ![]() заведомо неотрицательны). Следовательно, необходимо рассматривать значения угла из диапазона
заведомо неотрицательны). Следовательно, необходимо рассматривать значения угла из диапазона ![]() , иными словами кривая должна располагаться выше полярной оси и её продолжения. Как видите, та же история, что и в двух предыдущих параграфах.
, иными словами кривая должна располагаться выше полярной оси и её продолжения. Как видите, та же история, что и в двух предыдущих параграфах.
Пример 5
Вычислить площадь поверхности, образованной вращением кардиоиды ![]() вокруг полярной оси.
вокруг полярной оси.
Решение: график данной кривой можно посмотреть в Примере 6 урока о полярной системе координат. Кардиоида симметрична относительно полярной оси, поэтому рассматриваем её верхнюю половинку на промежутке ![]() (что, собственно, обусловлено и вышесказанным замечанием).
(что, собственно, обусловлено и вышесказанным замечанием).
Поверхность вращения будет напоминать яблочко.
Техника решения стандартна. Найдём производную по «фи»:
![]()
Составим и упростим корень:

Надеюсь, с заштатными тригонометрическими формулами ни у кого не возникло затруднений.
Используем формулу:
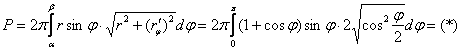
На промежутке ![]() , следовательно:
, следовательно: ![]() (о том, как правильно избавляться от корня, я подробно рассказал в статье Длина дуги кривой).
(о том, как правильно избавляться от корня, я подробно рассказал в статье Длина дуги кривой).

Ответ: ![]()
Интересное и короткое задание для самостоятельного решения:
Пример 6
Вычислить площадь шарового пояса ![]() ,
, ![]()
Что такое шаровой пояс? Положите на стол круглый неочищенный апельсин и возьмите в руки нож. Сделайте два параллельных разреза, разделив тем самым фрукт на 3 части произвольных размеров. Теперь возьмите серединку, у которой сочная мякоть обнажилась с обеих сторон. Данное тело называется шаровым слоем, а ограничивающая её поверхность (оранжевая кожура) – шаровым поясом.
Читатели, хорошо знакомые с полярными координатами, легко представили чертёж задачи: уравнение ![]() задаёт окружность с центром в полюсе радиуса
задаёт окружность с центром в полюсе радиуса ![]() , от которой лучи
, от которой лучи ![]() отсекают меньшую дугу. Данная дуга вращается вокруг полярной оси и таким образом получается шаровой пояс.
отсекают меньшую дугу. Данная дуга вращается вокруг полярной оси и таким образом получается шаровой пояс.
Теперь можно с чистой совестью и лёгким сердцем съесть апельсинку, на этой вкусной ноте и завершим занятие, не портить же вам аппетит другими примерами =)
Решения и ответы:
Пример 2: Решение: вычислим площадь поверхности, образованной вращением верхней ветви ![]() вокруг оси абсцисс. Используем формулу
вокруг оси абсцисс. Используем формулу  .
.
В данном случае: ![]() ;
;
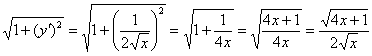
Таким образом:

Ответ: ![]()
Пример 4: Решение: используем формулу  . Первая арка циклоиды определена на отрезке
. Первая арка циклоиды определена на отрезке ![]() .
.
Найдём производные:
![]()
Составим и упростим корень:

Таким образом, площадь поверхности вращения:

На промежутке ![]() , поэтому
, поэтому ![]()

Первый интеграл интегрируем по частям:

Во втором интеграле используем тригонометрическую формулу ![]() .
.

Ответ: ![]()
Пример 6: Решение: используем формулу:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright