


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Примеры решений произвольных тройных интегралов.
Физические приложения тройного интеграла
Во 2-й части урока мы отработаем технику решения произвольных тройных интегралов ![]() , у которых подынтегральная функция трёх переменных
, у которых подынтегральная функция трёх переменных ![]() в общем случае отлична от константы и непрерывна в области
в общем случае отлична от константы и непрерывна в области ![]() ; а также познакомимся с физическими приложениями тройного интеграла
; а также познакомимся с физическими приложениями тройного интеграла
Вновь прибывшим посетителям рекомендую начать с 1-й части, где мы рассмотрели основные понятия и задачу нахождения объема тела с помощью тройного интеграла. Остальным же предлагаю немного повторить производные функции трёх переменных, поскольку в примерах данной статьи мы будем использовать обратную операцию – частное интегрирование функции ![]() .
.
Кроме того, есть ещё один немаловажный момент: если у Вас неважное самочувствие, то прочтение этой странички по возможности лучше отложить. И дело не только в том, что сейчас возрастёт сложность вычислений – у большинства тройных интегралов нет надёжных способов ручной проверки, поэтому к их решению крайне нежелательно приступать в утомлённом состоянии. При пониженном тонусе целесообразно порешать что-нибудь попроще либо просто отдохнуть (я терпелив, подожду =)), чтобы в другой раз со свежей головой продолжить расправу над тройными интегралами:
Пример 13
Вычислить тройной интеграл

На практике тело также обозначают буквой ![]() , но это не очень хороший вариант, ввиду того, «вэ» «зарезервировано» под обозначение объёма.
, но это не очень хороший вариант, ввиду того, «вэ» «зарезервировано» под обозначение объёма.
Сразу скажу, чего делать НЕ НАДО. Не нужно пользоваться свойством линейности и представлять интеграл в виде ![]() . Хотя, если очень хочется, то можно. В конце концов, есть и небольшой плюс – запись будет хоть и длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.
. Хотя, если очень хочется, то можно. В конце концов, есть и небольшой плюс – запись будет хоть и длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.
В алгоритме решения новизны будет немного. Сначала нужно разобраться с областью интегрирования. Проекция тела на плоскость ![]() представляет собой до боли знакомый треугольник:
представляет собой до боли знакомый треугольник:
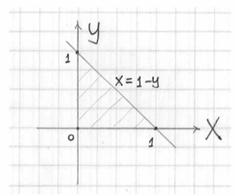
Сверху тело ограничено плоскостью ![]() , которая проходит через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной плоскостью
, которая проходит через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной плоскостью ![]() , т.е. решаем простейшую систему:
, т.е. решаем простейшую систему: ![]() – нет, данная прямая (на чертеже отсутствует) «проходит мимо», и проекция тела на плоскость
– нет, данная прямая (на чертеже отсутствует) «проходит мимо», и проекция тела на плоскость ![]() действительно представляет собой треугольник.
действительно представляет собой треугольник.
Не сложен здесь и пространственный чертёж:
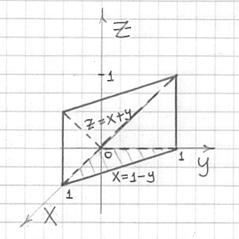
В действительности можно было ограничиться только им, поскольку проекция очень простая. …Ну, или только чертежом проекции, так как тело тоже простое =) Однако совсем ничего не чертить, напоминаю – плохой выбор.
Выберем следующий порядок обхода тела:
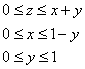
И перейдём к повторным интегралам:

Актуализируем следующее элементарное правило:
Когда функция ![]() интегрируется по какой-либо переменной, то два других аргумента считаются константами. То есть принцип точно такой же, как и при нахождении частных производных от функции трёх переменных, что естественно.
интегрируется по какой-либо переменной, то два других аргумента считаются константами. То есть принцип точно такой же, как и при нахождении частных производных от функции трёх переменных, что естественно.
Разбираемся с интегралами:
1) 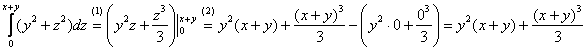
(1) При интегрировании по «зет» ![]() и
и ![]() считаются константами. В данном случае присутствует только «игрек», но это не меняет дела. Советую всегда мысленно либо на черновике выполнять проверку. Найдём частную производную по «зет»:
считаются константами. В данном случае присутствует только «игрек», но это не меняет дела. Советую всегда мысленно либо на черновике выполнять проверку. Найдём частную производную по «зет»:
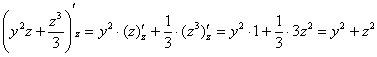 , что и требовалось проверить.
, что и требовалось проверить.
(2) Теперь используем формулу Ньютона-Лейбница: сначала ВМЕСТО «зет» подставляем верхний предел интегрирования ![]() , затем – нижний предел (ноль). В результате буквы «зет» остаться не должно!
, затем – нижний предел (ноль). В результате буквы «зет» остаться не должно!
Сносим трофей в следующий интеграл. По существу, решение свелось к двум переменным и к двойному интегралу:

(1) Используем свойство линейности интеграла, принимая во внимание тот факт, что «игрек» считается константой. Следует отметить, что не возбраняется оставить интеграл единым, раскрыть скобки и привести подобные слагаемые, но это менее рациональный способ (можете попробовать).
(2) Используем метод подведения под знак дифференциала. Если рассуждения воспринимаются совсем тяжело, мысленно замените «игрек» каким-нибудь конкретным числом, например, «пятёркой».
(3) Интегрируем по «икс» и выполняем проверку:
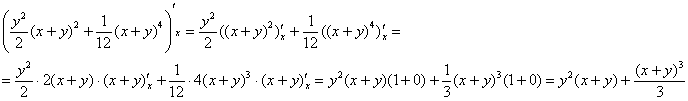
(4) Используем формулу Ньютона-Лейбница. Сначала ВМЕСТО «икс» (переменной, по которой проводилось интегрирование) подставляем ![]() , затем – ноль. После подстановок буквы «икс» остаться не должно!
, затем – ноль. После подстановок буквы «икс» остаться не должно!
Причёсываем результат и сносим его в последний интеграл, не теряя находящуюся там константу:

Ответ: ![]()
Результат безразмерен – просто число и всё.
Следующий пример для самостоятельного решения:
Пример 14
Вычислить тройной интеграл
Примерный образец оформления задачи в конце урока.
До сих пор мы рассматривали два способа решения – это проецирование на плоскость ![]() и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело можно спроецировать на любую из 3 координатных плоскостей и каждую проекцию обойти 2 путями. Таким образом, получается 6 способов решения. И логично предположить, что в общем случае некоторые из них проще, а некоторые – труднее.
и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело можно спроецировать на любую из 3 координатных плоскостей и каждую проекцию обойти 2 путями. Таким образом, получается 6 способов решения. И логично предположить, что в общем случае некоторые из них проще, а некоторые – труднее.
Наверняка многие обратили внимание, что в Примере № 13 я выбрал более редкий порядок обхода проекции, хотя ничто не мешало пойти «обычным» путём. Это не случайность.
В результате нахождения интеграла  получена сумма
получена сумма ![]() , в которой чуть выгоднее считать константой именно «игрек», что при прочих равных условиях (из уравнения прямой
, в которой чуть выгоднее считать константой именно «игрек», что при прочих равных условиях (из уравнения прямой ![]() одинаково легко выразить
одинаково легко выразить ![]() ) упрощает решение. А в некоторых задачах выбор порядка интегрирования и вовсе становится ОЧЕНЬ важным:
) упрощает решение. А в некоторых задачах выбор порядка интегрирования и вовсе становится ОЧЕНЬ важным:
Пример 15
Вычислить тройной интеграл

Решение: область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед:
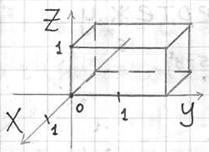
У незамысловатых областей можно не обращать внимания на проекцию и придерживаться следующего правила: обход тела осуществляется в направлениях координатных осей. Пределы интегрирования здесь очевидны
![]()
Но вот с порядком обхода не всё так просто. Если выбрать традиционный путь и сначала интегрировать по «зет», то получается неприятный интеграл  , который нужно брать по частям. Аналогичная история, если интегрировать по «игрек»:
, который нужно брать по частям. Аналогичная история, если интегрировать по «игрек»:  , тут даже дважды по частям.
, тут даже дважды по частям.
Наиболее выгодным путём является первоочередное интегрирование по «икс», в этом случае переменные ![]() , а значит, и множитель
, а значит, и множитель ![]() считаются константами:
считаются константами:
![]()
Перед тем, как подставить пределы интегрирования, не помешает проверка:
![]() – получена исходная подынтегральная функция.
– получена исходная подынтегральная функция.
![]()
Буква «икс» испарилась, как оно и должно быть.
Осталось 2 направления обхода ![]() , и следующий интеграл рациональнее взять по «зет» чтобы множитель
, и следующий интеграл рациональнее взять по «зет» чтобы множитель ![]() считался константой:
считался константой:

Промежуточная проверка:
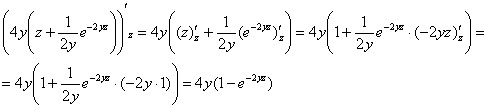
Гуд.
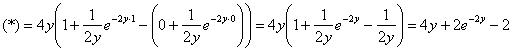
В качестве дополнительного контроля снова смотрим, исчезла ли после подстановки переменная, по которой интегрировали («зет»).
И, наконец, оставшееся направление обхода ![]() и оставшийся интеграл:
и оставшийся интеграл:

Проверка: ![]()
![]()
При подстановках следует проявлять повышенное внимание, так, например, при подстановке нуля в выражение ![]() второе слагаемое можно машинально счесть за ноль.
второе слагаемое можно машинально счесть за ноль.
На чистовике, конечно же, не нужно всё расписывать так подробно, анализ порядка интегрирования и промежуточные проверки осуществляются мысленно либо на черновике. Решение оформляется стандартно в 3 пункта, но читатели с хорошим уровнем подготовки могут записать его и «одной строкой»:

Ответ: ![]()
Наверное, это понятно, но на всякий случай закомментирую: буквенные множители-константы следует перемещать справа налево последовательно и без «перескоков» – до тех пор, пока каждая буква «не встретит свой интеграл». Условный пример:
![]()
Аналогичное задание для самостоятельного решения:
Пример 16
Вычислить тройной интеграл

Примерный образец чистового оформления задачи в конце урока.
Чем дальше, тем интереснее:
Физические приложения тройного интеграла
Но сначала разомнёмся физически, тело – в дело =) Пожалуйста, встаньте и найдите какой-нибудь пакет или мешок. Можно коробку. Теперь походим по квартире, ну или по улице и наведём порядок. А именно, наполним тару мусором. …Очень хорошо, молодцы. В результате ваших трудов получено ограниченное тело неоднородной плотности. Как говорится, есть бумажка, а есть жестяная крышка. Воздух, кстати, тоже обладает вполне определённой плотностью. Напоминаю, что физическая плотность – есть отношение массы к объёму, например, 100 грамм на кубический метр.
Ставим мешок рядышком и читаем дальше. Рассмотрим неоднородное (переменной плотности) тело ![]() . Если известна непрерывная в области
. Если известна непрерывная в области ![]() функция
функция ![]() плотности тела, то его масса равна следующему тройному интегралу:
плотности тела, то его масса равна следующему тройному интегралу:
![]()
Возможно, не всем понятен смысл функции плотности. Поясняю: если взять произвольную точку ![]() , принадлежащую телу
, принадлежащую телу ![]() , то значение функции
, то значение функции ![]() будет равно плотности тела в данной точке.
будет равно плотности тела в данной точке.
Только не стОит находить функцию ![]() для пакета с мусором, иначе шнобелевская премия обеспечена =) …Хотя, с другой стороны нашлись же энтузиасты оценить суммарную площадь поверхности индийских слонов и создать математическую модель пивной пены.
для пакета с мусором, иначе шнобелевская премия обеспечена =) …Хотя, с другой стороны нашлись же энтузиасты оценить суммарную площадь поверхности индийских слонов и создать математическую модель пивной пены.
Однако разрядились, и хватит. Разберём несколько тематических задач:
Пример 17
Вычислить массу неоднородного тела, ограниченного поверхностями ![]() , если известна функция его плотности
, если известна функция его плотности ![]() .
.
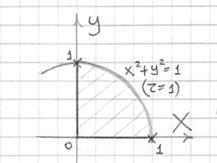
Решение: искомое тело ограничено цилиндром ![]() сбоку, эллиптическим параболоидом
сбоку, эллиптическим параболоидом ![]() – сверху и плоскостью
– сверху и плоскостью ![]() – снизу. Дополнительные условия
– снизу. Дополнительные условия ![]() «загоняют нас» в 1-й октант, и проекция тела на плоскость
«загоняют нас» в 1-й октант, и проекция тела на плоскость ![]() представляет собой соответствующую «четвертинку» единичного круга:
представляет собой соответствующую «четвертинку» единичного круга:
Аналитическим методом уточним высоту, на которой параболоид пересекает цилиндр:
 и выполним пространственный чертёж:
и выполним пространственный чертёж:
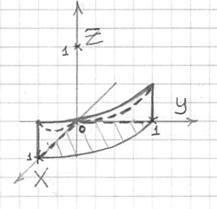
Проекция сразу же наводит на мысль о переходе к цилиндрической системе координат:

Порядок обхода тела очевиден:
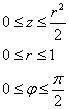
Таким образом:

Вычисления элементарны:

Ответ: ![]()
Следующий пример для самостоятельного решения:
Пример 18
Вычислить массу неоднородного тела, ограниченного поверхностями ![]() , если известна функция его плотности
, если известна функция его плотности ![]() .
.
Краткое решение в конце урока
И старая песня о главном:
Центр тяжести тела
Подобно тому, как задача о вычислении центра тяжести плоской фигуры решалась с помощью двойного интеграла, задача об отыскании центра тяжести тела решается аналогичным способом с помощью тройного интеграла.
Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести, то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени не реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.
Центр тяжести ![]() неоднородного тела
неоднородного тела ![]() рассчитывается по формулам:
рассчитывается по формулам:
 , где
, где ![]() – функция плотности тела, а
– функция плотности тела, а ![]() – масса тела.
– масса тела.
Если тело однородно (золотое, серебряное, платиновое и т.д.), то формулы упрощаются. Так как плотность ![]() постоянна, и масса
постоянна, и масса ![]() – есть произведение плотности на объём, получаем:
– есть произведение плотности на объём, получаем:
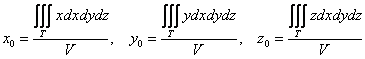 , а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла
, а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла ![]() .
.
Для центра тяжести однородного тела справедливы следующие утверждения:
– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);
– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;
– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.
Как видите, практически полная аналогия с центром тяжести плоской фигуры.
Ну и, само собой, не могу не порадовать вас заключительной задачей:
Пример 19
Найти центр тяжести однородного тела, ограниченного поверхностями ![]() ,
, ![]() . Выполнить чертежи данного тела и его проекции на плоскость
. Выполнить чертежи данного тела и его проекции на плоскость ![]() .
.
Решение: искомое тело ограничено координатными плоскостями и плоскостью ![]() , которую в целях последующего построения удобно представить в отрезках:
, которую в целях последующего построения удобно представить в отрезках: ![]() . Выберем «а» за единицу масштаба и выполним трёхмерный чертёж:
. Выберем «а» за единицу масштаба и выполним трёхмерный чертёж:
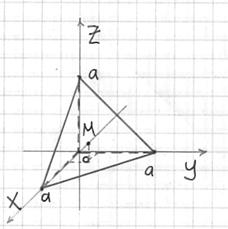
На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.
Проекция тела на плоскость ![]() очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости
очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости ![]() нужно решить систему:
нужно решить систему:
![]()
Подставляем значение ![]() в 1-е уравнение:
в 1-е уравнение: ![]() и получаем уравнение
и получаем уравнение ![]() «плоской» прямой:
«плоской» прямой:
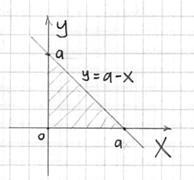
Координаты ![]() центра тяжести
центра тяжести ![]() тела
тела ![]() вычислим по формулам
вычислим по формулам
 , где
, где ![]() – объём тела.
– объём тела.
Выберем «классический» порядок обхода:
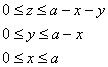
1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем случае параллелепипед представляет собой куб с ребром «а», и соответственно: ![]()
Осталось аккуратно провести чистовые вычисления (желающие могут потренироваться и выполнить их самостоятельно). В примерах с громоздкими преобразованиями рекомендую записывать решение столбиком – меньше шансов запутаться:

Дело за тремя тройными интегралами. ...А вы, наверное, не так давно и представить себе не могли, что окажетесь в эпицентре такого кошмара =)
2) Вычислим «иксовый» интеграл:

Таким образом, «иксовая» координата центра тяжести:

Ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь тела».
Ввиду симметрии тетраэдра две другие координаты должны получиться такими же. Теперь ошибочный ответ практически исключён!
3) Следующая «простыня»:

В результате:
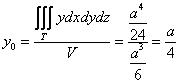
4) И заключительный, более короткий интеграл:

Отмечаем на чертеже найденную точку центра тяжести и её же записываем в
ответ: ![]()
Осталось взять мешок с мусором и чувством глубокого морального удовлетворения выбросить его… нет, в окно не надо =)
Что осталось за кадром? В сетку урока не попала редко встречающая на практике сферическая система координат, в которой положение любой точки пространства однозначно определяется одним расстоянием и двумя углами. И до сферических координат у меня таки дошли пальцы в статье Дивергенция векторного поля.
Вы постоянно сетовали на простоту примеров, и поэтому я просто не мог вам не рассказать о криволинейных и поверхностных интегралах, а также основах векторного анализа.
Желаю успехов!
Решения и ответы:
Пример 14: Решение: изобразим проекцию данного тела на плоскость ![]() :
:

Сверху тело ограничено эллиптическим параболоидом ![]() .
.
Выберем следующий порядок обхода:
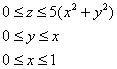
Таким образом:

Примечание: в «зетовом» интеграле сумма ![]() считается константой, поэтому её удобно сразу вынести в следующий интеграл.
считается константой, поэтому её удобно сразу вынести в следующий интеграл.

Ответ: ![]()
Пример 16: Решение: выполним чертёж:
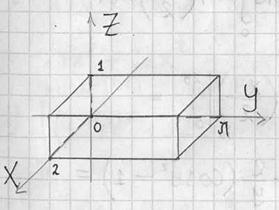
Выберем следующий порядок обхода тела:
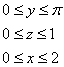
Таким образом:

Ответ: ![]()
Пример 18: Решение: искомое тело ограничено эллиптическим параболоидом ![]() снизу и конической поверхностью
снизу и конической поверхностью ![]() – сверху; параболоид и конус пересекаются в плоскости
– сверху; параболоид и конус пересекаются в плоскости ![]() по окружности
по окружности ![]() (выкладки и чертёж – см. в Примере № 9 страницы Тройные интегралы). Поскольку
(выкладки и чертёж – см. в Примере № 9 страницы Тройные интегралы). Поскольку ![]() , то речь идёт о правом (относительно плоскости
, то речь идёт о правом (относительно плоскости ![]() ) полупространстве, и проекцией тела на плоскость
) полупространстве, и проекцией тела на плоскость ![]() является верхний полукруг единичного радиуса:
является верхний полукруг единичного радиуса:
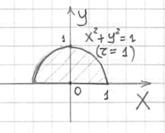
Массу тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат:

Порядок обхода тела:

Таким образом:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright