


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как найти сумму ряда?
Рассмотрим небольшую задачу, которая обычно предлагается в самом начале практической работы по теме. И такая привилегия не случайна. Для решения типового примера на нахождение суммы ряда не требуется тяжёлый багаж признаков сравнения, признаков Даламбера, Коши и т.д. – достаточно самых минимальных знаний о числовых рядах. Необходимо понимать, что такое ряд ![]() , уметь расписывать его подробно и не округлять глаза после словосочетаний «ряд сходится», «ряд расходится», «сумма ряда». Поэтому, если ваше настроение совсем на нуле, пожалуйста, уделите 5-10 минут статье Ряды для чайников (буквально первые 2-3 страницы), а потом возвращайтесь сюда и смело начинайте решать примеры!
, уметь расписывать его подробно и не округлять глаза после словосочетаний «ряд сходится», «ряд расходится», «сумма ряда». Поэтому, если ваше настроение совсем на нуле, пожалуйста, уделите 5-10 минут статье Ряды для чайников (буквально первые 2-3 страницы), а потом возвращайтесь сюда и смело начинайте решать примеры!
Следует отметить, что в большинстве случаев найти сумму ряда непросто, и этот вопрос обычно решается через функциональные ряды (доживём-доживём:)). Так, например, сумма популярного артиста ![]() выводится через ряды Фурье. В этой связи на практике почти всегда требуется установить сам факт сходимости, но не найти конкретное число
выводится через ряды Фурье. В этой связи на практике почти всегда требуется установить сам факт сходимости, но не найти конкретное число ![]() (многие, думаю, уже успели это заметить). Однако среди великого множества числовых рядов есть немногочисленные представители, которые позволяют без особых проблем прикоснуться к святая святых даже полному чайнику. И на вводном уроке я приводил пример бесконечно убывающей геометрической прогрессии
(многие, думаю, уже успели это заметить). Однако среди великого множества числовых рядов есть немногочисленные представители, которые позволяют без особых проблем прикоснуться к святая святых даже полному чайнику. И на вводном уроке я приводил пример бесконечно убывающей геометрической прогрессии ![]() , сумма
, сумма ![]() которой легко рассчитывается по известной школьной формуле.
которой легко рассчитывается по известной школьной формуле.
В данной статье мы продолжим рассматривать похожие примеры, кроме того, узнаем строгое определение суммы и попутно познакомимся с некоторыми свойствами рядов. Разомнёмся… да прямо на прогрессиях и разомнёмся:
Пример 1
Найти сумму ряда

Решение: представим наш ряд в виде суммы двух рядов:

Почему в данном случае так можно сделать? Выполненные действия основаны на двух простейших утверждениях:
1) Если сходятся ряды ![]() , то будут сходиться и ряды, составленные из сумм или разностей соответствующих членов:
, то будут сходиться и ряды, составленные из сумм или разностей соответствующих членов: ![]() . При этом существенно то обстоятельство, что речь идёт о сходящихся рядах. В нашём примере мы заранее знаем, что обе геометрические прогрессии сойдутся, а значит, без всяких сомнений раскладываем исходный ряд в два ряда.
. При этом существенно то обстоятельство, что речь идёт о сходящихся рядах. В нашём примере мы заранее знаем, что обе геометрические прогрессии сойдутся, а значит, без всяких сомнений раскладываем исходный ряд в два ряда.
2) Второе свойство ещё очевиднее. Константу ![]() можно вынести за пределы ряда:
можно вынести за пределы ряда: ![]() , и это не повлияет на его сходимость или расходимость и итоговую сумму. Зачем выносить константу? Да просто чтобы она «не мешалась под ногами». Но иногда бывает выгодно этого и не делать
, и это не повлияет на его сходимость или расходимость и итоговую сумму. Зачем выносить константу? Да просто чтобы она «не мешалась под ногами». Но иногда бывает выгодно этого и не делать
Чистовое оформление примера выглядит примерно так:

Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: ![]() , где
, где ![]() – первый член прогрессии,
– первый член прогрессии, ![]() – основание прогрессии.
– основание прогрессии.

Ответ: сумма ряда ![]()
Начало решения можно оформить несколько в другом стиле – расписать ряд напрямую и перегруппировать его члены:

Дальше по накатанной.
Пример 2
Найти сумму ряда

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Каких-либо особых изысков здесь нет, но однажды мне попался необычный ряд ![]() , который может застать врасплох неискушенного человека. Это… тоже бесконечно убывающая геометрическая прогрессия! Действительно,
, который может застать врасплох неискушенного человека. Это… тоже бесконечно убывающая геометрическая прогрессия! Действительно, ![]() , и сумма рассчитывается буквально за пару мгновений:
, и сумма рассчитывается буквально за пару мгновений: ![]() .
.
А сейчас живительный глоток математического анализа, необходимый для решения дальнейших задач:
Что такое сумма ряда?
Строгое определение сходимости/расходимости и суммы ряда в теории даётся через так называемые частичные суммы ряда. Частичные – значит неполные. Распишем частичные суммы числового ряда ![]() :
:

И особую роль играет частичная сумма «эн» членов ряда:
![]()
Если предел частичных сумм числового ряда ![]() равен конечному числу:
равен конечному числу: ![]() , то такой ряд называют сходящимся, а само число
, то такой ряд называют сходящимся, а само число ![]() – суммой ряда. Если же предел
– суммой ряда. Если же предел ![]() бесконечен либо его не существует, то ряд называют расходящимся.
бесконечен либо его не существует, то ряд называют расходящимся.
Вернёмся к демонстрационному ряду ![]() и распишем его частичные суммы:
и распишем его частичные суммы:

Предел частичных сумм ![]() – есть в точности бесконечно убывающая геометрическая прогрессия, сумма которой равна:
– есть в точности бесконечно убывающая геометрическая прогрессия, сумма которой равна: ![]() . Похожий предел мы рассматривали на уроке о числовых последовательностях. Собственно, и сама формула
. Похожий предел мы рассматривали на уроке о числовых последовательностях. Собственно, и сама формула ![]() – это прямое следствие вышеизложенных теоретических выкладок (см. 2-ой том матана).
– это прямое следствие вышеизложенных теоретических выкладок (см. 2-ой том матана).
Таким образом, прорисовывается общий алгоритм решения нашей задачи: необходимо составить энную частичную сумму ряда ![]() и найти предел
и найти предел ![]() . Посмотрим, как это осуществляется на практике:
. Посмотрим, как это осуществляется на практике:
Пример 3
Вычислить сумму ряда
![]()
Решение: на первом шаге нужно разложить общий член ряда в сумму дробей. Используем метод неопределённых коэффициентов:

В результате:

Сразу же полезно провести обратное действие, выполнив тем самым проверку:
![]()
Получен общий член ряда в исходном виде, следовательно, разложение в сумму дробей проведено успешно.
Теперь составим частичную сумму ряда ![]() . Вообще это делается устно, но один раз я максимально подробно распишу, что откуда взялось:
. Вообще это делается устно, но один раз я максимально подробно распишу, что откуда взялось:

Как записать ![]() совершенно понятно, но чему равен предыдущий член
совершенно понятно, но чему равен предыдущий член ![]() ? В общий член ряда
? В общий член ряда ![]() ВМЕСТО «эн» подставляем
ВМЕСТО «эн» подставляем ![]() :
:
![]()
Почти все слагаемые частичной суммы благополучно взаимоуничтожаются:
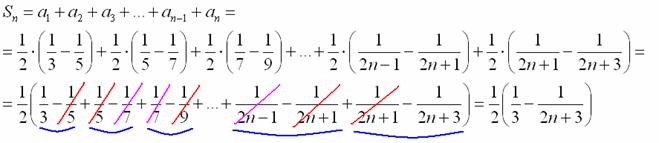
Прямо такие пометки и делаем карандашом в тетради. Чертовски удобно.
Осталось вычислить элементарный предел и узнать сумму ряда:

Ответ: ![]()
Аналогичный ряд для самостоятельного решения:
Пример 4
Вычислить сумму ряда
![]()
Примерный образец чистового оформления решения в конце урока.
Очевидно, что нахождение суммы ряда – это само по себе доказательство его сходимости (помимо признаков сравнения, Даламбера, Коши и др.), о чём, в частности, намекает формулировка следующего задания:
Пример 5
Найти сумму ряда или установить его расходимость
![]()
По внешнему виду общего члена можно сразу сказать, как ведёт себя этот товарищ. Без комплексов. С помощью предельного признака сравнения легко выяснить (причём даже устно), что данный ряд будет сходиться вместе с рядом ![]() . Но перед нами редкий случай, когда без особых хлопот рассчитывается ещё и сумма.
. Но перед нами редкий случай, когда без особых хлопот рассчитывается ещё и сумма.
Решение: разложим знаменатель дроби в произведение. Для этого нужно решить квадратное уравнение:

Таким образом:
![]()
Множители лучше расположить в порядке возрастания: ![]() .
.
Выполним промежуточную проверку:
![]()
ОК
Таким образом, общий член ряда:
![]()
Методом неопределённых коэффициентов разложим его в сумму дробей:

Коэффициенты получились целые и это радует:
![]()
На всякий случай выполним ещё одну промежуточную проверку:
![]()
ОК
Поэтапные проверки – королевы зачётов ;-)
Составим энную частичную сумму и уничтожим всё, что можно уничтожить:

Как видите, в этот раз противоположные числа не расположены рядышком. Поэтому на практике всегда лучше перестраховаться и записать побольше членов ряда – чтобы наверняка понять, какие слагаемые исчезнут, а какие – нет. По той же причине крайне желательно выполнять пометки карандашом.
Опыт показывает, что чаще всего студенты испытывают затруднения с хвостом суммы. В этой связи ещё раз повторим принцип, по которому записаны члены ![]() . Отчего ж не повторить?
. Отчего ж не повторить?
В общий член ряда ![]() :
:
– ВМЕСТО «эн» подставляем ![]() :
: ![]() ;
;
– ВМЕСТО «эн» подставляем ![]() :
: ![]() ;
;
– ВМЕСТО «эн» подставляем ![]() :
: ![]() .
.
На завершающем этапе находим сумму ряда:

Ответ: ![]()
Изящный ряд для самостоятельного решения:
Пример 6
Найти сумму ряда или установить его расходимость
![]()
Решение и ответ в конце урока.
Вероятно, на этом рубеже у многих посетителей возникла уверенность в своих навыках и желание раствориться на просторах Интернета. Рекомендую немного задержаться, поскольку ниже по течению среди, казалось бы, такого однообразия приветливо моргают глазами большие крокодилы.
Усложняем задание и набиваем руку:
Пример 7
Вычислить сумму ряда
![]()
Решение: со знаменателем тут никаких проблем:
![]()
Множители, как я уже отмечал, целесообразно расположить в порядке возрастания.
Используем метод неопределённых коэффициентов:

Здесь на последних шагах проведено почленное сложение двух уравнений системы.
Таким образом: ![]()
Не ленимся:
![]()
Что и требовалось проверить.
Запишем частичную сумму «эн» членов ряда, при этом обращаем внимание на тот факт, что «счётчик» ряда «начинает работать» с номера ![]() . Как и в предыдущих примерах, надёжнее растянуть кобру на приличную длину:
. Как и в предыдущих примерах, надёжнее растянуть кобру на приличную длину:
![]()
Однако если мы запишем ![]() в одну-две строчки, то всё равно будет довольно трудно сориентироваться в слагаемых (их таки 3 в каждом члене). И здесь нам на помощь придёт… геометрия. Заставим плясать змею под свою дудочку:
в одну-две строчки, то всё равно будет довольно трудно сориентироваться в слагаемых (их таки 3 в каждом члене). И здесь нам на помощь придёт… геометрия. Заставим плясать змею под свою дудочку:

Да, прямо так и пишем в тетради один член под другим и прямо так их вычёркиваем. Кстати, собственное изобретение. Как понимаете, не от самого лёгкого задания в этой жизни =)
В результате зачистки получаем:
![]()
И, наконец, сумма ряда:

Ответ: ![]()
Готово.
Пример 8
Вычислить сумму ряда
![]()
Это пример для самостоятельного решения.
Рассматриваемая задача, конечно, не радует нас разнообразием – на практике встречается либо бесконечно убывающая геометрическая прогрессия, либо ряд с дробно-рациональным общим членом и разложимым многочленом в знаменателе (к слову, далеко не каждый такой многочлен даёт возможность найти сумму ряда). Но, тем не менее, иногда попадаются необычные экземпляры, и по сложившейся доброй традиции я завершаю урок какой-нибудь любопытной задачей:
Пример 9
Вычислить сумму ряда, если она существует
![]()
Решение: формулировка уже интригует. Интересен тот факт, что все члены данного ряда отрицательны. Почему? На интервале ![]() логарифм меньше нуля, а за счёт аргумента
логарифм меньше нуля, а за счёт аргумента ![]() при любом натуральном «эн» (начиная с
при любом натуральном «эн» (начиная с ![]() ) мы каждый раз и попадаем в этот интервал.
) мы каждый раз и попадаем в этот интервал.
Таким образом, если ряд сходится, то будет отрицательна и его сумма. Только вот есть мааааленькая проблемка – найти это значение, если оно существует =)
Алгоритм такой же, главное, догадаться, с какой стороны подступиться к решению. Предыдущий опыт подсказывает, что нужно попытаться представить общий член ряда в виде суммы двух или бОльшего количества слагаемых. Из этих соображений преобразуем выражение в скобках и используем свойства логарифма:

Ну что же, выглядит вполне перспективно, давайте разберёмся с частичной суммой ряда:
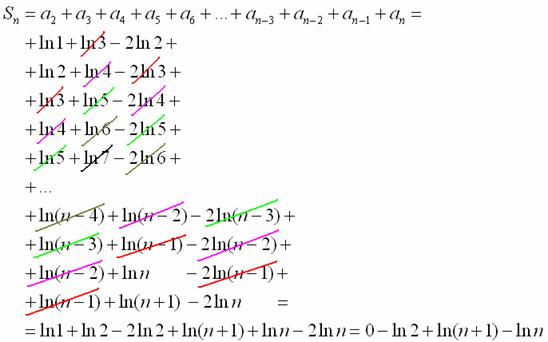
В целях устранения неопределённости вновь используем свойство логарифма:

Получено конечное число, а значит, ряд сходится. Как и ожидалось, сумма получилась отрицательной.
Ответ: ![]()
Поздравляю со знаменательным событием! Коль скоро вы читаете эти строки, то сегодня на вашу долю выпал редкий и счастливый случай – когда в частичной сумме ![]() ряда удалось массово ликвидировать слагаемые. Удалось же? =)
ряда удалось массово ликвидировать слагаемые. Удалось же? =)
Не каждый день бывает! Но то ли ещё будет ;-)
Решения и ответы:
Пример 2: Решение:

Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: ![]() .
.
Для первого ряда: ![]() , для второго ряда:
, для второго ряда: ![]() .
.

Ответ: сумма ряда ![]()
Пример 4: Решение: Методом неопределенных коэффициентов разложим общий член ряда в сумму дробей:

Таким образом:

Найдём частичную сумму ряда:

Вычислим сумму ряда:

Ответ: ![]()
Пример 6: Решение: разложим знаменатель общего члена в произведение и методом неопределённых коэффициентов получим сумму дробей:

Таким образом: ![]()
Составим частичную сумму и проведём упрощения:

Вычислим сумму ряда:

Ответ: ![]()
Пример 8: Решение: представим общий член ряда в виде:
![]()
Методом неопределённых коэффициентов разложим его в сумму дробей:

Таким образом: 
Запишем частичную сумму:
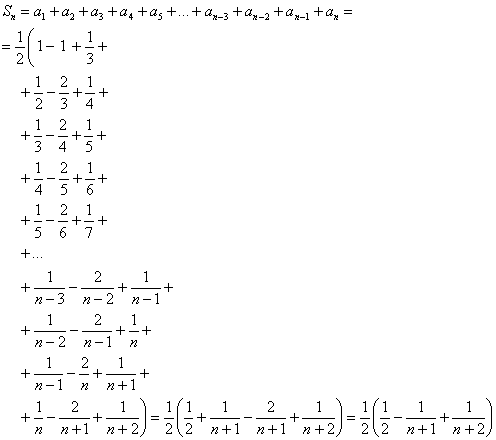
Вычислим сумму ряда:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright