Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Показательное распределение вероятностей

Продолжаем изучать особые виды распределений непрерывной случайной величины. Показательным или экспоненциальным называют распределение, которое характеризуется следующей функцией плотности:
, где

Убедимся в том, что перед нами не «подделка». Поскольку  и несобственный интеграл:
, то функция  действительно задаёт закон распределения НСВ.

Большим достоинством показательного распределения является тот факт, что оно определяется всего лишь одним параметром. Всего лишь одним, Карл! …нет, лучше, конечно, вообще отсутствие параметров, но дальше их количество будет только возрастать =)

Как-то так получилось, что во всех примерах статьи о равномерном распределении мы начинали с функции , и поэтому для разнообразия зайдём в лес с другой стороны:

Задача

Непрерывная случайная величина  задана своей функцией распределения:

Требуется:

1) определить коэффициент ;
2) найти плотность распределения вероятностей ;
3) схематично построить графики функций  и ;
4) вычислить математическое ожидание и дисперсию ;
5) определить вероятность того, что  примет значение из интервала .

Одним словом, обычная задача на НСВ бессмысленная и беспощадная.

Решаем:

1) В силу непрерывности функции распределения:
 – при этом и только при этом значении предложенная функция задаёт закон распределения  непрерывной случайной величины:

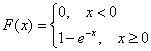
Пока, кстати, мы не знаем, что это за закон, ведь вверху я привёл другое определение.

2) Найдём функцию плотности распределения:

надеюсь, все в ладах с производной сложной функции: .

Ну вот, теперь избушка повернулась к нам передом, а к лесу задом. Поскольку данная функция имеет вид , то случайная величина  распределена показательно. Даже образцово-показательно, т.к. значение  наиболее приятно.

3) Условие допускает схематическое построение графиков, но зачем занижать планку? Даже при их ручном построении не составляет никакого труда найти пару дополнительных точек и проявить маломальскую аккуратность.

Вычислим пару значений  и простенький предел . Таким образом, прямая  является горизонтальной асимптотой для графика  при :

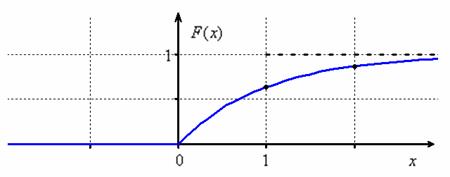
Показательное распределение нашло широкое применение в прикладных задачах, и пока чертёж «не уехал вверх» я приведу конкретный пример. Пусть переменная «икс» обозначает время и в момент времени  начинает эксплуатироваться некий прибор, например, обычная лампочка. Случайная величина  – время  работы лампочки до перегорания. Тогда функция  описывает вероятность того, что лампочка проработает МЕНЬШЕ, чем прошедшее время . И по понятным причинам при увеличении  эта вероятность стремится к единице, что хорошо иллюстрирует вышеприведённый график.

Кстати, о чём идёт речь в 5-м пункте условия? В контексте рассматриваемого примера, нам нужно найти  – вероятность того, что лампочка проработает более 2 тыс. часов (значения, естественно, условные). Давайте сразу и вычислим эту вероятность:

Ситуацию наглядно иллюстрирует чертёж ПЛОТНОСТИ распределения вероятностей:

Площадь между графиком  и осью абсцисс равна единице (проверено в начале статьи), и значительная часть этой площади (а именно, ) сосредоточена на промежутке от 0 до 2.

Применительно к «электрическому» примеру, определённый интеграл 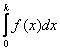равен вероятности того, что лампочка проработает от 0 до тыс. часов. В частности, как раз:
.

И, наверное, все поняли, что несобственный интеграл – есть вероятность того, что лампочка проработает более  тыс. часов, и Пункт 5 можно решить вторым способом:

4) Вычислим математическое ожидание и дисперсию.

Здесь есть короткий путь, и есть универсальный. Начнём с общей формулы математического ожидания, которая приводит нас к следующему несобственному интегралу:

Сначала удобно найти неопределенный интеграл:

Вспоминаем интегрирование по частям:

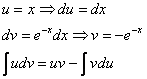
, произвольную константу приплюсовывать не надо, т.к. она всё равно сократится:

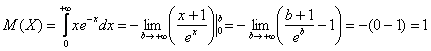
Дробь  по той причине, что знаменатель более высокого порядка роста, чем числитель.

…вот видите, как нам пригодился математический анализ, а вы всё говорили «зачем это нужно, зачем это нужно» =)

Дисперсию вычислим по формуле:

И из избушки на курьих ножках появляется следующий интеграл:

Как и в случае с матожиданием, сначала проясним первообразную:

По канонам жанра тут нужно дважды интегрировать по частям, но решение облегчается тем, что после 1-го применения формулы  мы сталкиваемся с только что решённым интегралом:

Таким образом, несобственный интеграл:

Здесь  по той же самой причине – порядок роста.

И, наконец, дисперсия:

«Наконец», потому что Пункт 5) уже разобран вместе с его ламповым смыслом =)

Пункты решения можно переставлять, т.к. они бывают расположены неудобно, а иногда и совершенно несуразно.

Готово.

Показательное распределение нашло широкое применение в теории надёжности, и этой теме даже посвящены отдельные главы учебного пособия В.Е. Гмурмана. Помимо лампочек и более грустных примеров существуют и другие приложения. Так, например, в простейшем потоке событий, время ожидания каждого последующего события распределено по экспоненциальному закону. Проанализируйте работу диспетчера такси самостоятельно.

И для самостоятельного решения я предлагаю вам не только интересное, но ещё и крайне полезное Задание:

1) Дать определение показательного распределения вторым способом, с помощью функции распределения.

В начале статьи я привёл формулировку через плотность , и теперь ваша очередь – найдите функцию  и запишите грамотный ответ на поставленный вопрос.

2) Вывести формулы математического ожидания и дисперсии.

Фактически тут нужно решить задачу в общем виде.

3) Записать закон распределения для  и вычислить  и .

Полученными формулами можно пользоваться и на практике, но с оглядкой. Будьте готовы к тому, что вас попросят привести подробные выкладки.

Дополнительных примеров с показательным распределением совсем немного. Впрочем, мы только что охватили все возможные случаи =) Вот она, мощь одного параметра.

Да, в сводном справочнике по теории вероятностей, конечно, приведены все частные формулы, но очень важно, чтобы вы умели получать их самостоятельно, исходя из общих определений. Это один из основополагающих принципов изучения математики, который красной нитью проходит через все её разделы.

Ну а сейчас пришло время зажечь новые огни  и перейти к кульминационной статье под названием Нормальное распределение вероятностей.

Интересного чтения!

Решение задания:

1) Составим функцию :
– На интервале  и .
– На промежутке , следовательно:

Показательным называют распределение, которое характеризуется функцией:
, где

2) Вычислим математическое ожидание:
 

Сначала найдём неопределённый интеграл:

Интегрируем по частям:

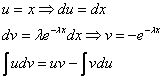
Таким образом:

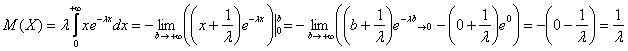
Дисперсию вычислим по формуле:

В данном случае:

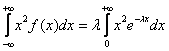
Сначала найдём неопределенный интеграл:

Интегрируем по частям:

чтобы воспользоваться уже известным интегралом, умножим и разделим на «лямбда»:

Несобственный интеграл:

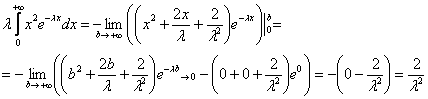
Таким образом, дисперсия:

3) Запишем показательный закон для :

Вычислим математическое ожидание и дисперсию:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте