


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить центр тяжести плоской ограниченной фигуры
с помощью двойного интеграла?
Данная статья посвящена наиболее распространённому на практике приложению двойного интеграла – вычислению центра тяжести плоской ограниченной фигуры. Многие читатели интуитивно понимают, что такое центр тяжести, но, тем не менее, рекомендую повторить материал одного из уроков аналитической геометрии, где я разобрал задачу о центре тяжести треугольника и в доступной форме расшифровал физический смысл этого термина.
В самостоятельных и контрольных заданиях для решения, как правило, предлагается простейший случай – плоская ограниченная однородная фигура, то есть фигура постоянной физической плотности – стеклянная, деревянная, оловянная чугунные игрушки, тяжёлое детство и т.д. Далее по умолчанию речь пойдёт только о таких фигурах =)
Первое правило и простейший пример: если у плоской фигуры есть центр симметрии, то он является центром тяжести данной фигуры. Например, центр круглой однородной пластины. Логично и по-житейски понятно – масса такой фигуры «справедливо распределена во все стороны» относительно центра. Верти – не хочу.
Однако в суровых реалиях вам вряд ли подкинут сладкую эллиптическую шоколадку, поэтому придётся вооружиться серьёзным кухонным инструментом:
Координаты ![]() центра тяжести
центра тяжести ![]() плоской однородной ограниченной фигуры
плоской однородной ограниченной фигуры ![]() рассчитываются по следующим формулам:
рассчитываются по следующим формулам:
 , или:
, или:
 , где
, где ![]() – площадь области
– площадь области ![]() (фигуры); или совсем коротко:
(фигуры); или совсем коротко:
![]() , где
, где ![]()
Интеграл ![]() будем условно называть «иксовым» интегралом, а интеграл
будем условно называть «иксовым» интегралом, а интеграл ![]() – «игрековым» интегралом.
– «игрековым» интегралом.
Примечание-справка: для плоской ограниченной неоднородной фигуры, плотность которой задана функцией ![]() , формулы более сложные:
, формулы более сложные:
 , где
, где ![]() – масса фигуры; в случае однородной плотности
– масса фигуры; в случае однородной плотности ![]() они упрощаются до вышеприведённых формул.
они упрощаются до вышеприведённых формул.
На формулах, собственно, вся новизна и заканчивается, остальное – это ваше умение решать двойные интегралы, кстати, сейчас предоставляется прекрасная возможность потренироваться и усовершенствовать свою технику. А совершенству, как известно, нет предела =)
Закинемся бодрящей порцией парабол:
Пример 1
Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями ![]() .
.
Решение: линии здесь элементарны: ![]() задаёт ось абсцисс, а уравнение
задаёт ось абсцисс, а уравнение ![]() – параболу, которая легко и быстро строится с помощью геометрических преобразований графиков:
– параболу, которая легко и быстро строится с помощью геометрических преобразований графиков:
![]() – парабола
– парабола ![]() , сдвинутая на 2 единицы влево и на 1 единицу вниз.
, сдвинутая на 2 единицы влево и на 1 единицу вниз.
Я выполню сразу весь чертёж с готовой точкой ![]() центра тяжести фигуры:
центра тяжести фигуры:
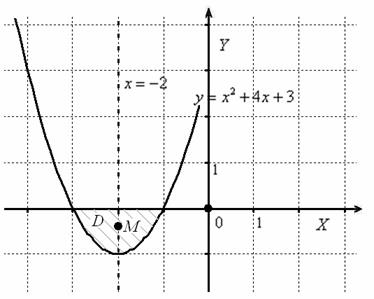
Правило второе: если у фигуры существует ось симметрии, то центр тяжести данной фигуры обязательно лежит на этой оси.
В нашем случае фигура симметрична относительно прямой ![]() , то есть фактически мы уже знаем «иксовую» координату
, то есть фактически мы уже знаем «иксовую» координату ![]() точки «эм».
точки «эм».
Также обратите внимание, что по вертикали центр тяжести смещён ближе к оси абсцисс, поскольку там фигура более массивна.
Полезная рекомендация: ещё до вычислений постарайтесь определить примерное расположение центра тяжести «на глазок» – это поможет проверить полученные значения ![]() на предмет явных ошибок.
на предмет явных ошибок.
Да, возможно, ещё не все до конца поняли, что такое центр тяжести: пожалуйста, поднимите вверх указательный палец и мысленно поставьте на него заштрихованную «подошву» точкой ![]() . Теоретически фигура не должна упасть.
. Теоретически фигура не должна упасть.
Координаты центра тяжести фигуры найдём по формулам ![]() , где
, где ![]() .
.
Порядок обхода области ![]() (фигуры) здесь очевиден:
(фигуры) здесь очевиден:
![]()
Внимание! Определяемся с наиболее выгодным порядком обхода один раз – и используем его для всех интегралов!
1) Сначала вычислим площадь фигуры. Ввиду относительной простоты интеграла решение можно оформить компактно, главное, не запутаться в вычислениях:

Смотрим на чертёж и прикидываем по клеточкам площадь. Получилось около дела.
2) Иксовая координата ![]() центра тяжести уже найдена «графическим методом», поэтому можно сослаться на симметрию и перейти к следующему пункту. Однако так делать всё-таки не советую – велика вероятность, что решение забракуют с формулировкой «используйте формулу».
центра тяжести уже найдена «графическим методом», поэтому можно сослаться на симметрию и перейти к следующему пункту. Однако так делать всё-таки не советую – велика вероятность, что решение забракуют с формулировкой «используйте формулу».
В этой связи координату лучше рассчитать формально. Вычислим «иксовый» интеграл:

Заметьте, что здесь можно обойтись исключительно устными вычислениями – иногда совсем не обязательно приводить дроби к общему знаменателю или мучить калькулятор.
Таким образом:
 , что и требовалось получить.
, что и требовалось получить.
3) Найдём ординату ![]() центра тяжести. Вычислим «игрековый» интеграл:
центра тяжести. Вычислим «игрековый» интеграл:

А вот тут без калькулятора пришлось бы тяжко. На всякий случай закомментирую, что в результате умножения многочленов ![]() получается 9 членов, причём некоторые из них подобны. Подобные слагаемые я привёл устно (как это обычно принято делать в похожих случаях) и сразу записал итоговую сумму
получается 9 членов, причём некоторые из них подобны. Подобные слагаемые я привёл устно (как это обычно принято делать в похожих случаях) и сразу записал итоговую сумму ![]() .
.
В результате:
 , что очень и очень похоже на правду.
, что очень и очень похоже на правду.
На заключительном этапе отмечаем на чертеже точку ![]() . По условию не требовалось ничего чертить, но в большинстве задач мы волей-неволей вынуждены изобразить фигуру. Зато есть безусловный плюс – визуальная и довольно эффективная проверка результата.
. По условию не требовалось ничего чертить, но в большинстве задач мы волей-неволей вынуждены изобразить фигуру. Зато есть безусловный плюс – визуальная и довольно эффективная проверка результата.
Ответ: ![]()
Следующие два примера для самостоятельного решения.
Попроще:
Пример 2
Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями ![]()
Кстати, если вы представляете, как расположена парабола ![]() и увидели точки, в которых она пересекает ось
и увидели точки, в которых она пересекает ось ![]() , то здесь и на самом деле можно обойтись без чертежа.
, то здесь и на самом деле можно обойтись без чертежа.
И посложнее:
Пример 3
Найти центр тяжести однородной плоской фигуры, ограниченной линиями ![]()
В случае затруднений с построением графиков, изучите (повторите) урок о параболах и/или Пример №11 статьи Двойные интегралы для чайников.
Примерные образцы решений в конце урока.
Кроме того, десяток-другой похожих примеров можно найти в соответствующем архиве на странице Готовые решения по высшей математике.
Ну а я не могу не порадовать любителей высшей математики, которые часто просят меня разбирать и трудные задачки:
Пример 4
Найти центр тяжести однородной плоской фигуры, ограниченной линиями ![]() . Фигуру и её центр тяжести изобразить на чертеже.
. Фигуру и её центр тяжести изобразить на чертеже.
Решение: условие данной задачи уже категорично требует выполнения чертежа. А ведь требование не настолько и формально! – эту фигуру способен представить в уме даже человек со средним уровнем подготовки:
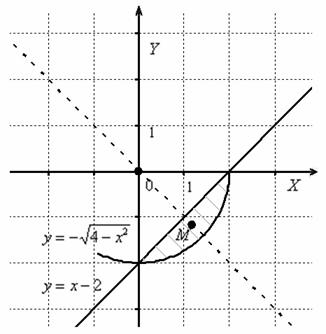
Прямая ![]() рассекает круг на 2 части, и дополнительная оговорка
рассекает круг на 2 части, и дополнительная оговорка ![]() (см. линейные неравенства) указывает на то, что речь идёт именно о маленьком заштрихованном кусочке.
(см. линейные неравенства) указывает на то, что речь идёт именно о маленьком заштрихованном кусочке.
Фигура симметрична относительно прямой ![]() (изображена пунктиром), поэтому центр тяжести должен лежать на данной линии. И, очевидно, что его координаты равны по модулю. Отличный ориентир, практически исключающий ошибочный ответ!
(изображена пунктиром), поэтому центр тяжести должен лежать на данной линии. И, очевидно, что его координаты равны по модулю. Отличный ориентир, практически исключающий ошибочный ответ!
Теперь плохая новость =) На горизонте маячит малоприятный интеграл от корня, который мы подробно разобрали в Примере №4 урока Эффективные методы решения интегралов. И кто его знает, что там нарисуется ещё. Казалось бы, ввиду наличия окружности выгодно перейти к полярной системе координат, однако не всё так просто. Уравнение прямой ![]() преобразуется к виду
преобразуется к виду ![]() и интегралы тоже получатся не сахарные (хотя фанаты тригонометрических интегралов оценят). В этой связи осмотрительнее остановиться на декартовых координатах.
и интегралы тоже получатся не сахарные (хотя фанаты тригонометрических интегралов оценят). В этой связи осмотрительнее остановиться на декартовых координатах.
Порядок обхода фигуры:
![]()
1) Вычислим площадь фигуры:

Первый интеграл рациональнее взять подведением под знак дифференциала:

А во втором интеграле проведём стандартную замену:

![]()
Вычислим новые пределы интегрирования:


Весьма достоверно, едем дальше:
2) Найдём ![]() .
.

Здесь во 2-м интеграле опять был использован метод подведения функции под знак дифференциала. Отработайте и возьмите на вооружение эти оптимальные (по моему мнению) приёмы решения типовых интегралов.

После непростых и длительных вычислений вновь обращаем свой взор на чертёж (помним, что точки ![]() мы пока не знаем!) и получаем глубокое моральное удовлетворение от найденного значения
мы пока не знаем!) и получаем глубокое моральное удовлетворение от найденного значения ![]() .
.
3) Исходя из проведённого ранее анализа, осталось убедиться, что ![]() .
.

Отлично:

Изобразим точку ![]() на чертеже. В соответствии с формулировкой условия запишем её как окончательный ответ:
на чертеже. В соответствии с формулировкой условия запишем её как окончательный ответ: ![]()
Похожее задание для самостоятельного решения:
Пример 5
Найти центр тяжести однородной плоской фигуры, ограниченной линиями ![]() . Выполнить чертёж.
. Выполнить чертёж.
Эта задача интереса тем, что в ней задана фигура достаточно малых размеров, и если где-нибудь допустить ошибку, то высока вероятность вообще «не попасть» в область. Что, безусловно, хорошо с точки зрения контроля решения.
Примерный образец оформления в конце урока.
Иногда бывает целесообразен переход к полярным координатам в двойных интегралах. Это зависит от фигуры. Искал-искал у себя удачный пример, но не нашёл, поэтому продемонстрирую ход решения на 1-й демо-задаче указанного выше урока:
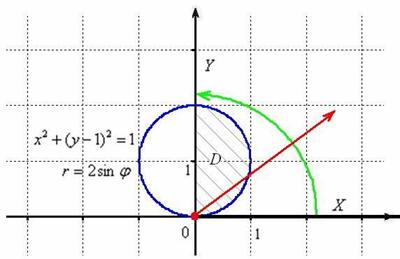
Напоминаю, что в том примере мы перешли к полярным координатам, выяснили порядок обхода области ![]() и вычислили её площадь
и вычислили её площадь ![]()
Давайте найдём центр тяжести данной фигуры. Схема та же: ![]() . Значение
. Значение ![]() просматривается прямо из чертежа, а «иксовая» координата должна быть смещена чуть ближе к оси ординат, поскольку там располагается более массивная часть полукруга.
просматривается прямо из чертежа, а «иксовая» координата должна быть смещена чуть ближе к оси ординат, поскольку там располагается более массивная часть полукруга.
В интегралах ![]() используем стандартные формулы перехода:
используем стандартные формулы перехода:


Правдоподобно, скорее всего, не ошиблись.

Примечание: интеграл ![]() подробно разобран в Примере №9 урока Интегралы от тригонометрических функций.
подробно разобран в Примере №9 урока Интегралы от тригонометрических функций.
 , что и требовалось получить.
, что и требовалось получить.
Готово.
Как-то так невзначай на этой странице уместились 17 двойных интегралов, что является полнейшим безобразием, по причине того, что за окном жаркие деньки июня, которые совсем не располагают к учёбе.
Успешной сдачи сессии!
Решения и ответы:
Пример 2: Решение: выполним чертёж:
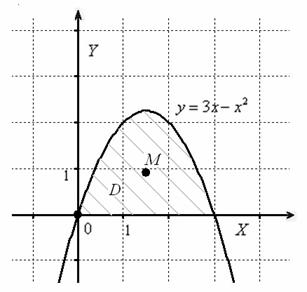
Координаты центра тяжести фигуры найдём по формулам ![]() , где
, где ![]() .
.
Порядок обхода области:
![]()
1) Вычислим площадь фигуры:

2) Найдём абсциссу ![]() центра тяжести.
центра тяжести.


3) Найдём ординату ![]() центра тяжести.
центра тяжести.


Ответ: ![]()
Пример 3: Решение: выполним чертеж:
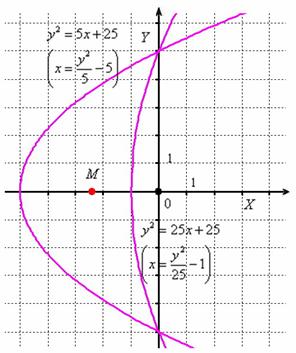
Выберем следующий порядок обхода фигуры:

Найдём центр тяжести ![]() . Используем формулы
. Используем формулы ![]() , где
, где ![]()
1) Вычислим площадь фигуры:

2) Найдём абсциссу ![]() центра тяжести.
центра тяжести.

3) Найдём ординату ![]() центра тяжести.
центра тяжести.

(интеграл от нечетной функции по симметричному относительно нуля отрезку)

Ответ: ![]()
Пример 5: Решение: выразим функции в явном виде:

Выполним чертеж:

Выберем следующий порядок обхода фигуры:

По соответствующим формулам найдём координаты ![]() центра тяжести
центра тяжести ![]() данной фигуры.
данной фигуры.

В первом интеграле проведем замену:

Новые пределы интегрирования:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright