


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Сумма степенного ряда
Данный урок лучше всего изучать по «горячим следам» сразу же после статьи о разложении функции в степенные ряды, поскольку сейчас мы будем решать обратную задачу. Пожалуйста, откройте таблицу разложений функций в степенные ряды и по возможности отправьте файл на печать – чтобы справочный материал был постоянно перед глазами. На бумаге, на столе и перед глазами. Это важно!
Суть задания предельно простА: дан степенной ряд. Например:
![]()
И по условию требуется найти сумму этого ряда, то есть, функцию, к которой он сходится. …Не понятно, что значит «ряд сходится к функции»? Срочно читаем предыдущую статью!
Как найти сумму степенного ряда? Здесь не существует какого-то жёсткого алгоритма решения, но есть общие ориентиры, с которыми мы сегодня и познакомимся.
В первую очередь целесообразно обратиться к таблице и попытаться выяснить – НА КАКОЕ РАЗЛОЖЕНИЕ больше всего похож предложенный ряд? У нашего ряда в знаменателях по порядку идут факториалы, и поэтому он больше всего напоминает разложение экспоненты: ![]() . Однако тут степени «альф» совпадают с номерами факториалов, а у нас степень «икса» «отстаёт» на единицу. Что делать? Поправим ситуацию умножением и делением ряда на «икс»:
. Однако тут степени «альф» совпадают с номерами факториалов, а у нас степень «икса» «отстаёт» на единицу. Что делать? Поправим ситуацию умножением и делением ряда на «икс»:
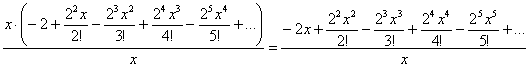
Теперь обращаем внимание, что наверху не хватает слагаемого-«единички». Да какие проблемы? – прибавим её да вычтем:
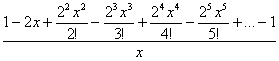
Что смущает ещё? Знакочередование. Его в разложении экспоненты нет. Но в данном случае «минусы» можно «затолкать» под нечётные степени, а под чётными степенями их «возродить»:
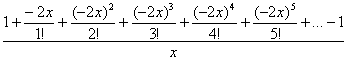
Таким образом, мы сконструировали разложение экспоненты для ![]() :
:
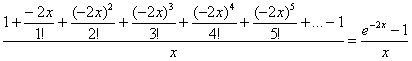
Итак:
![]()
Другим немаловажным вопросом является область сходимости ряда. Иными словами, ПРИ КАКИХ значениях «икс» наш ряд будет сходиться к функции ![]() ? В таблице указано, что экспоненциальный ряд сходится при любом «альфа», но у нас есть одна загвоздочка: найденная функция не определена в точке
? В таблице указано, что экспоненциальный ряд сходится при любом «альфа», но у нас есть одна загвоздочка: найденная функция не определена в точке ![]() . Однако ряд в этой точке сходится! И действительно – если подставить ноль, то получается конечное число:
. Однако ряд в этой точке сходится! И действительно – если подставить ноль, то получается конечное число:
![]()
Таким образом, сумма ряда запишется кусочным образом:
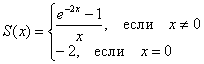
Как и сумма числового ряда, она стандартно обозначается буквой «эс».
Причём, интересно отметить, что данная сумма непрерывна. И в самом деле – используя соответствующий замечательный предел, получаем:
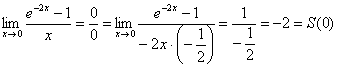
Однако в точке ![]() ряд сходится всё же НЕ к функции
ряд сходится всё же НЕ к функции ![]() (и похожие примеры, кстати, уже встретились в статье о разложении функции в ряд).
(и похожие примеры, кстати, уже встретились в статье о разложении функции в ряд).
Несмотря на то, что интервалы сходимости типовых рядов я указал в таблице, важно понимать, откуда они взялись. Как, например, определить область сходимости только что разобранного ряда безо всякой таблицы? Записываем его в свёрнутом виде, подобрав общий член:
![]()
и, пользуясь обычным алгоритмом, выясняем, что ряд сходится на всей числовой прямой.
С помощью найденной суммы ![]() легко рассчитать сумму любого числового ряда из этого «семейства». Так, например, при
легко рассчитать сумму любого числового ряда из этого «семейства». Так, например, при ![]() получаем ряд
получаем ряд ![]() , сумма которого равна:
, сумма которого равна: ![]() – на всякий случай напомню, что это сумма всех его членов:
– на всякий случай напомню, что это сумма всех его членов:
![]()
Если ![]() , то получим ряд
, то получим ряд 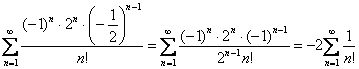
с суммой 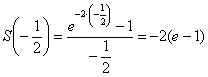 , откуда, кстати, открывается волнующая тайна:
, откуда, кстати, открывается волнующая тайна:
![]() .
.
И так далее – можно рассмотреть любое значение «икс» из области сходимости ряда.
В статье о сумме числовых рядов мы потихонечку долбили их ломом (да и то немногие поддавались), и сейчас в наших руках оказался целый отбойный молоток! Пользуйтесь и наслаждайтесь!
Другой пример: ![]() – найдём сумму данного степенного ряда.
– найдём сумму данного степенного ряда.
Именно в свёрнутом виде он чаще всего и предлагается, и само собой ряд удобно расписать:
![]()
Анализируя таблицу, приходим к выводу, что наш «пациент» больше всего напоминает разложение ![]() , причём «альфа», очевидно, равно «иксу» в кубе. Выносим за скобки «минус» и «лишний»
, причём «альфа», очевидно, равно «иксу» в кубе. Выносим за скобки «минус» и «лишний» ![]() и показываем, что
и показываем, что ![]() :
:
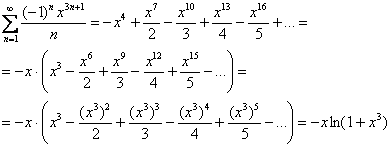
Определим, на каком промежутке ряд ![]() сходится к функции
сходится к функции ![]() . Интервал сходимости ряда можно найти опять же стандартным способом, либо воспользоваться табличным «подарком»:
. Интервал сходимости ряда можно найти опять же стандартным способом, либо воспользоваться табличным «подарком»:
![]()
![]()
Сходимость ряда на концах интервала выясняем как обычно – прямой подстановкой:
если ![]() , то
, то ![]() – расходится;
– расходится;
если ![]() , то
, то ![]() – сходится условно.
– сходится условно.
Таким образом, ряд ![]() сходится лишь на полуинтервале
сходится лишь на полуинтервале ![]() . Вне этого промежутка он расходится и его суммы, понятное дело, не существует.
. Вне этого промежутка он расходится и его суммы, понятное дело, не существует.
Итак: ![]() , если
, если ![]() – в отличие от предыдущего примера, выбор «иксов» тут небогат.
– в отличие от предыдущего примера, выбор «иксов» тут небогат.
И здесь ещё хочется заострить внимание на разнице в понятиях и обозначениях:
через ![]() обозначается функция (сама по себе),
обозначается функция (сама по себе),
а через ![]() – конкретно сумма ряда (на том или ином промежутке).
– конкретно сумма ряда (на том или ином промежутке).
Разминочные задания для самостоятельного решения:
Найти сумму следующих степенных рядов:
а) ![]()
…ну а кому сейчас легко? =)
б) ![]()
Дополнительно: записать числовой ряд для ![]() и вычислить его сумму.
и вычислить его сумму.
Краткие решения и ответы в конце урока.
Наверное, все понимают, как выполнять проверку таких заданий – для этого нужно разложить полученную функцию обратно в ряд. Но это уже пройденное, да и к тому же простое действие, и поэтому я его расписывать не буду.
Алгебраические преобразования рядов могут быть весьма замысловаты, однако дело не ограничиваются только ими. Как многие подозревали, производные с интегралами поджидают нас и здесь! Ну а куда ж без них? =) Пожалуйста, освежите воспоминания с помощью таблицы производных и таблицы интегралов (откроются на соседних вкладках) – их тоже по возможности распечатайте и положите перед глазами. …Есть? Поехали:
Почленное дифференцирование и интегрирование степенного ряда
Пусть степенной ряд ![]() сходится к своей сумме
сходится к своей сумме ![]() на некотором промежутке. …Теоремы формулировать не буду – проще рассказать своими словами:
на некотором промежутке. …Теоремы формулировать не буду – проще рассказать своими словами:
Степенной ряд можно почленно дифференцировать в любой точке внутри его промежутка сходимости: 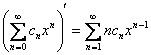 , при этом интервал сходимости полученного ряда останется точно таким же, а его сумма на данном интервале будет равна:
, при этом интервал сходимости полученного ряда останется точно таким же, а его сумма на данном интервале будет равна: ![]() .
.
И на всякий случай поясню, что значит «почленно» – если расписать ряд подробно, то согласно свойству линейности, он дифференцируется по каждому члену отдельно:
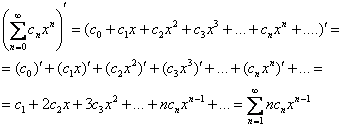
Степенной ряд можно почленно интегрировать внутри его промежутка сходимости, но здесь ситуация занятнее. Если мы будем его интегрировать по фиксированному отрезку ![]() , то получим числовой ряд:
, то получим числовой ряд:
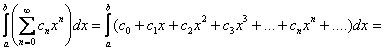
![]()
всё чинно-почленно:
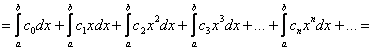
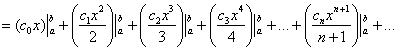 – и в самом деле, членами же этого ряда являются числа (вспоминаем формулу Ньютона-Лейбница).
– и в самом деле, членами же этого ряда являются числа (вспоминаем формулу Ньютона-Лейбница).
Геометрический смысл и практическое применение такого интегрирования мы разберём на уроке о приближённом вычислении интеграла, ну а сейчас нас ждут другие подвиги. А именно, почленное интегрирование по отрезку с переменным верхним пределом ![]() , где «икс» может принимать произвольное значение из интервала сходимости, при этом в качестве нижнего предела удобно выбрать ноль. По той же самой формуле Ньютона-Лейбница, получается уже не числовой, а функциональный ряд – распишу подробно:
, где «икс» может принимать произвольное значение из интервала сходимости, при этом в качестве нижнего предела удобно выбрать ноль. По той же самой формуле Ньютона-Лейбница, получается уже не числовой, а функциональный ряд – распишу подробно:

формально здесь можно сказать, что вместо «икс» мы подставляем «икс»:
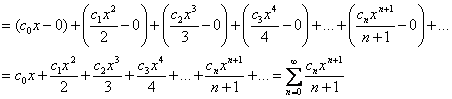
Причём: полученный ряд обладает тем же интервалом сходимости, что и исходный ряд, а его сумму можно найти по формуле 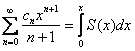 , где
, где ![]() , напоминаю – сумма ряда
, напоминаю – сумма ряда ![]()
Важнейшим условием осуществления этих действий является равномерная сходимость степенных рядов – анонсирую и рекомендую прочитать эту интереснейшую статью! Но прежде освоим технику. Начнём с тех же табличных разложений, некоторые из которых как раз получены с помощью дифференцирования и интегрирования.
Выведем, например, разложение арктангенса. Для этого разложим его производную ![]() в стандартный ряд
в стандартный ряд ![]() :
: ![]()
![]()
после чего проинтегрируем этот ряд в его интервале сходимости ![]() :
:
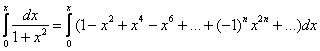
далее для краткости записи я буду дифференцировать/интегрировать ряды «один махом»:
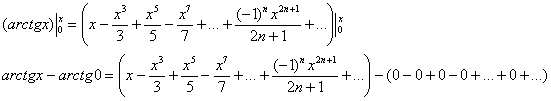
В результате:
![]()
Поскольку «родительский» биномиальный ряд сходится на интервале ![]() , то и полученный ряд
, то и полученный ряд ![]() тоже будет сходиться на этом интервале. А может быть ещё и на его концах. Проверяем:
тоже будет сходиться на этом интервале. А может быть ещё и на его концах. Проверяем:

Оба числовых ряда сходятся условно, таким образом, ряд ![]() сходится к арктангенсу в области
сходится к арктангенсу в области ![]() (вспоминаем картинку из предыдущей статьи).
(вспоминаем картинку из предыдущей статьи).
По этой же схеме выводятся разложения логарифма и арксинуса – потренируйтесь самостоятельно.
С помощью «новых» действий можно найти разложения некоторых других функций.
Классический Пример 1
Разложить в ряд функцию ![]() и указать его интервал сходимости.
и указать его интервал сходимости.
Решение: по «общим очертаниям» предложенная функция сильно напоминает производную от ![]() . И действительно:
. И действительно:
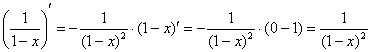
Таким образом, искомый ряд получается фактически на «автомате» – дифференцированием стандартного разложения на его интервале сходимости:
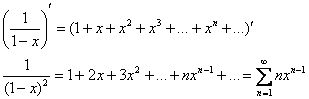
Так как исходный ряд сходится при ![]() , то полученный ряд тоже будет сходиться на данном интервале. Осталось узнать, что происходит на концах:
, то полученный ряд тоже будет сходиться на данном интервале. Осталось узнать, что происходит на концах:
![]() – расходится;
– расходится;
![]() – расходится.
– расходится.
Ответ: ![]() , ряд сходится при
, ряд сходится при ![]()
Выполним проверку:
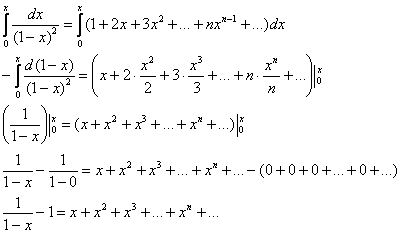
и перебрасываем единичку направо:
![]() – в результате получено исходное разложение, что и требовалось проверить.
– в результате получено исходное разложение, что и требовалось проверить.
Таким образом, всегда держите на заметке, что предложенная функция может быть производной либо интегралом от чего-нибудь табличного. Однако сегодняшний урок посвящён обратной задаче, и применительно к разобранной «классике» она формулируется так:
Пример 1*
Найти сумму ряда ![]()
А вот это уже труднее – ведь мы «ещё не знаем», что данный ряд получен дифференцированием ряда ![]() , и данный факт можно запросто не увидеть. Впрочем, тут существует чёткий критерий, позволяющий «прозреть»:
, и данный факт можно запросто не увидеть. Впрочем, тут существует чёткий критерий, позволяющий «прозреть»:
Решение: анализируя ряд ![]() , приходим к выводу, что он мало похож на что-то стандартное, но зато в таблице есть его «ближайший родственник»
, приходим к выводу, что он мало похож на что-то стандартное, но зато в таблице есть его «ближайший родственник» ![]() , к которому мы и обратимся за помощью.
, к которому мы и обратимся за помощью.
Для этого нужно «избавиться» от множителя ![]() . Каким образом? Разделить его на самого себя! И такую возможность нам предоставляет интегрирование – здесь я оформлю действия в свёрнутой форме:
. Каким образом? Разделить его на самого себя! И такую возможность нам предоставляет интегрирование – здесь я оформлю действия в свёрнутой форме:
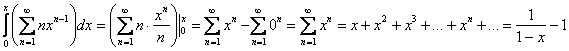
Теперь нужно «вернуть должок» дифференцированием:
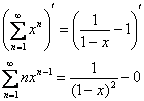
Ответ: ![]() на интервале
на интервале ![]()
Таким образом, «почленёнка» помогает нам «убрать с дороги» неудобные множители, и это действительно очень мощный инструмент:
Пример 2
Найти сумму степенного ряда
![]()
Но перед тем как решать, важная преамбула: несмотря на то, в условии этого не прописано – нам всё равно потребуется найти область сходимости ряда. Причина, думаю, понятна – ведь сумма в общем случае существует далеко не везде, и если в ответе указать только её, то это будет серьёзнейшим недочётом.
Наверное, многие уже «набили руку» на числовых рядах и способны найти область сходимости устно. В частности, здесь хорошо видно, что предложенный ряд сходится на промежутке ![]() . Как выполнить экспресс-анализ? Берём какую-нибудь правильную дробь, например,
. Как выполнить экспресс-анализ? Берём какую-нибудь правильную дробь, например, ![]() и выполняем подстановку:
и выполняем подстановку:
 – данный ряд сходится по признаку Даламбера. И, очевидно, что после подстановки любой дроби из интервала
– данный ряд сходится по признаку Даламбера. И, очевидно, что после подстановки любой дроби из интервала ![]() будут получаться похожие ряды.
будут получаться похожие ряды.
Далее тестируем произвольное «внешнее» значение, например ![]() :
:
![]() – расходится по тому же признаку Даламбера. Кстати, здесь вообще не выполнен необходимый признак сходимости, т. к.
– расходится по тому же признаку Даламбера. Кстати, здесь вообще не выполнен необходимый признак сходимости, т. к. ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() .
.
Проверка концов интервала тоже осуществляется в считанные секунды:
![]()
Таким образом, к решению задачи нужно подойти во «всеоружии» – с известной областью сходимости и записать следующую фразу: данный ряд сходится на ![]() . Как вариант, можно привести развёрнутые выкладки нахождения области – но это если вам трудно или если не лень.
. Как вариант, можно привести развёрнутые выкладки нахождения области – но это если вам трудно или если не лень.
Ну а теперь амбула (с). Во-первых, не будем торопиться с «тяжёлой артиллерией» – вдруг она не потребуется? Сначала распишем ряд подробно:
![]() и вновь обратим свой взор на таблицу…. – наш ряд напоминает разложение арктангенса, однако ж, там знакочередование, и никакими алгебраическими «ухищрениями» эти ряды не «состыковать». Другие табличные разложения подходят к нашему случаю ещё меньше.
и вновь обратим свой взор на таблицу…. – наш ряд напоминает разложение арктангенса, однако ж, там знакочередование, и никакими алгебраическими «ухищрениями» эти ряды не «состыковать». Другие табличные разложения подходят к нашему случаю ещё меньше.
Что делать? Глядя на степени «икса» и числа внизу, в голову приходит светлая мысль избавиться от последних. Дифференцируем ряд на его интервале сходимости ![]() :
:
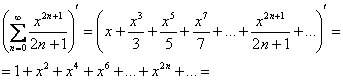
и всё дело свелось к простому табличному разложению:
![]()
Но коль скоро мы дифференцировали, то за это придётся «заплатить» интегрированием:
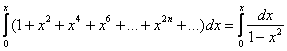
Справа в качестве суммы исходного ряда «нарисовался» «высокий» логарифм:
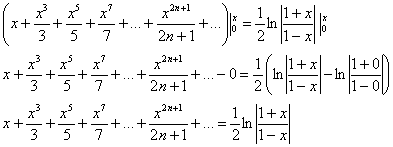
Ответ: ![]() на интервале
на интервале ![]()
Обратите внимание, что в решении фигурировал ряд ![]() с суммой
с суммой ![]() на том же интервале, но об этом нас никто не спрашивал.
на том же интервале, но об этом нас никто не спрашивал.
Сегодня я буду разбирать простые примеры, а вам предлагать интересные:))
Пример 3
Найти сумму ряда
![]()
Краткое решение и ответ в конце урока.
Но это ещё далеко не все секреты:
Пример 4
Найти сумму ряда
![]()
Решение: данный ряд сходится в области ![]() (проанализируйте, почему).
(проанализируйте, почему).
Как обычно расписываем ряд, чтобы поискать «лёгкий путь»:
![]() И после изучения таблицы и некоторых «трепыханий» мы приходим к грустному выводу, что ничего путного не получается. Очевидное дифференцирование тоже выглядит не особо перспективным:
И после изучения таблицы и некоторых «трепыханий» мы приходим к грустному выводу, что ничего путного не получается. Очевидное дифференцирование тоже выглядит не особо перспективным:
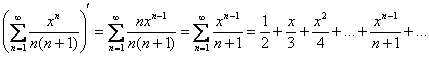
Но вот как бы было хорошо «избавиться» в знаменателе не от ![]() , а от
, а от ![]() . И возникает вопрос, а нельзя ли организовать такую возможность? Можно! Чтобы наверху получить
. И возникает вопрос, а нельзя ли организовать такую возможность? Можно! Чтобы наверху получить ![]() ряд следует искусственно умножить и разделить на «икс». Однако этим действием мы «выключаем из игры» точку
ряд следует искусственно умножить и разделить на «икс». Однако этим действием мы «выключаем из игры» точку ![]() , которая входит в область сходимости. И поэтому в ней необходимо вычислить сумму ряда:
, которая входит в область сходимости. И поэтому в ней необходимо вычислить сумму ряда: ![]() , чтобы жить спокойно:
, чтобы жить спокойно:
![]()
Прерываем решение «звёздочкой» и работаем с новым «кадром»:
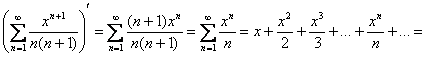
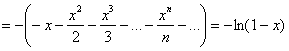 – здесь всё свелось к разложению
– здесь всё свелось к разложению ![]() для
для ![]() .
.
Выполняем обратное действие:
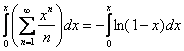
Интеграл правой части, надо сказать, неприятный, и поэтому с ним лучше разобраться отдельно, причём без пределов интегрирования:
![]()
и знакомый приём с дробями,… не запутаться бы тут в знаках:

Контроль: ![]()
![]() , ч. т. п.
, ч. т. п.
Таким образом:

И теперь главное не забыть про «звёздочку»:
![]()
Но это ещё не всё! Как подсказывает математическое чутьё, тонким местом исследования являются концы интервала сходимости – и действительно, полученная функция имеет проблемы не только с нулём, но ещё и на правом конце области сходимости ряда. Придётся исследовать его отдельно:
![]() – и к нашей радости сумма числового ряда отыскивается по стандартной схеме. Метод неопределённых коэффициентов работает в своей простейшёй ипостаси:
– и к нашей радости сумма числового ряда отыскивается по стандартной схеме. Метод неопределённых коэффициентов работает в своей простейшёй ипостаси:
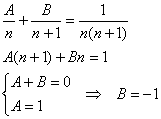
Таким образом: ![]()
Запишем частичную сумму ряда:
![]()
Сумма исследуемого числового ряда:
![]()
И, наконец, сумма ряда функционального:
Ответ: 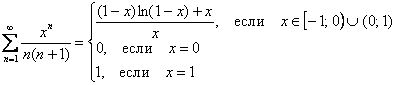
Такой вот простенький ряд =)
Следует отметить, что искусственный приём с домножением и делением на самом деле можно использовать и после «очевидного» дифференцирования, но там получатся более сложные вычисления.
Вам понравилось? Но и это ещё не всё! В свете последней части задания всплывает… какой же я тонкий лирик:))
второй способ решения: разложим числовую часть общего члена степенного ряда в сумму дробей (см. выше) и представим его в виде суммы двух рядов:
![]()
строго говоря, здесь нужны кой-какие комментарии, но я их опущу.
Дальнейшие действия очевидны – веник ломаем по прутикам:
1) 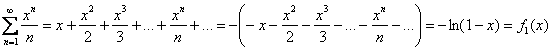
(берём на заметку значение ![]() )
)
2) 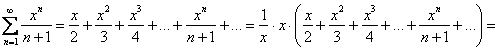
(берём на заметку значение ![]() )
)
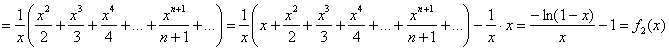
Таким образом, функция, к которой сходится ряд на промежутках ![]() :
:
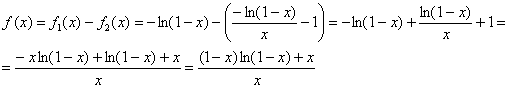
Точки ![]() исследуются отдельно, и что приятно, для последней уже есть готовенький числовой ряд
исследуются отдельно, и что приятно, для последней уже есть готовенький числовой ряд ![]() .
.
Ответ: 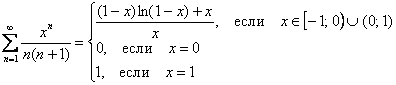
На всякого мудреца довольно простоты! И никакого дифференцирования с интегрированием =)
Кстати, не нужно думать, что этот способ является каким-то экзотическим – он используется во многих тематических заданиях, причём иной ряд можно разделить даже на 3 части.
Обещанная интересность для самостоятельного решения:
Пример 5
Найти сумму ряда
![]()
Примерный образец чистового оформления задачи в конце урока.
Кроме того, встречаются задачи, в которых приходится дифференцировать 2 раза подряд, что «карается» последующим двукратным интегрированием. При этом справедливо следующее…, а чего скромничать – изучим ситуацию в общем виде:
пусть функция ![]() разложима в степенной ряд
разложима в степенной ряд ![]() на некотором интервале:
на некотором интервале:
![]()
ну, или можно сказать, что сумма степенного ряда равна ![]() – смотря с какой стороны рассуждать.
– смотря с какой стороны рассуждать.
Как уже отмечалось, при почленном дифференцировании ряда ![]() на данном интервале получившийся ряд сойдётся к производной:
на данном интервале получившийся ряд сойдётся к производной:
![]()
При повторном дифференцировании на том же интервале суммой нового ряда будет вторая производная:
![]()
И более того, если у функции существуют все производные высших порядков, то дифференцировать можно до бесконечности:
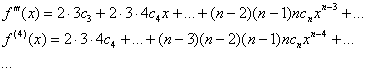
Причём, соответствующие ряды, не нужно быть пророком, сходятся к своим производным, а интервал сходимости не меняется.
И, разумеется, справедливы обратные выкладки с интегрированием. Но вместо них небольшой фокус – вычислим значения функции и всех её производных в точке ![]() :
:
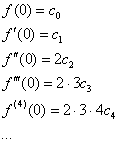
Далее выразим коэффициенты ![]() , …очевидно, что
, …очевидно, что ![]() – после чего подставим их в разложение
– после чего подставим их в разложение ![]() :
:
![]()
В большинстве задач этого урока мы сначала дифференцировали, а затем интегрировали, но само собой допустим и обратный порядок. Так, в Примере 1* всё было наоборот – и уже из этого простого ряда ![]() яснА основная задача первоочередного интегрирования – расчистить «верхний этаж»:
яснА основная задача первоочередного интегрирования – расчистить «верхний этаж»:
Пример 6
Найти сумму степенного ряда
![]()
Решение: данный ряд сходится на интервале ![]() .
.
И вновь не будем пренебрегать поиском простых путей:
![]() , …которых, увы, не видно.
, …которых, увы, не видно.
Очевидно, что основной нашей помехой является множитель ![]() , который надо «убрать». Попробуем проинтегрировать ряд почленно:
, который надо «убрать». Попробуем проинтегрировать ряд почленно:
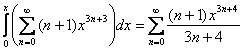
Не айс,… вот если бы внизу нарисовалось ![]() – тогда да. Но это ж можно организовать – нужно только понизить изначальную степень
– тогда да. Но это ж можно организовать – нужно только понизить изначальную степень ![]() на единицу. А делается это очень просто – «отщипываем» один «икс» и выносим его за пределы ряда:
на единицу. А делается это очень просто – «отщипываем» один «икс» и выносим его за пределы ряда:
![]()
Далее работаем с «модифицированным» рядом:

Приводим ситуацию в равновесие дифференцированием:
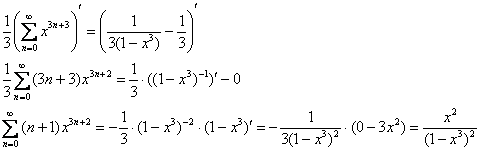
И не забываем, что это ещё не окончательная сумма:
![]()
Ответ: ![]() на интервале
на интервале ![]()
Заметьте, что здесь нет проблем со знаменателем, так как значение ![]() не входит в область сходимости ряда – не забываем контролировать такие моменты!
не входит в область сходимости ряда – не забываем контролировать такие моменты!
И в заключение…, нет, пожалуй, успокоительная задача:)
Пример 7
Найти сумму степенного ряда
![]()
Моя версия решения внизу страницы.
Наверное, у всех уже в глазах мельтешит от разложений, и поэтому самое время принять лекарство – равномерную сходимость ряда, которая по иронии судьбы и стала тому первопричиной :) Кроме того, на грядущем уроке вы узнаете, как определяется сумма произвольного функционального ряда.
Пожалуйста, сообщите, если где заметили опечатку или ошибку, потому что статья была действительно одна из самых кропотливых, и вы имели счастье, кстати, познакомиться с её 6-й версией. Всё время казалось «всё», но каждый раз всплывали… к концу статьи я превратился в толстого циника)… ещё какие-то интересные факты, примеры и нюансы. Что-то добавлялось, редактировалось, что-то «выбрасывалось». И на самом деле ещё есть о чём рассказать! Поэтому нужно пересилить себя и поставить
.
Решения и ответы:
Разминочное задание. Решение:
а) Распишем несколько членов ряда, раскроем скобки и перегруппируем слагаемые:
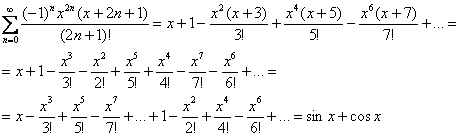
Оба разложения сходятся на всей числовой прямой.
Ответ: ![]() на интервале
на интервале ![]()
б) Ориентируемся на табличное разложение ![]() :
:
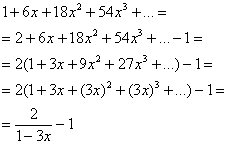
Найдём область сходимости ряда. Согласно таблице, ряд сходится при ![]() . В данном случае
. В данном случае ![]() :
:
![]() – разделим все части на три:
– разделим все части на три:
![]()
Исследуем сходимость ряда на концах найденного интервала. Для этого запишем его в свёрнутом виде ![]() и подставим граничные значения:
и подставим граничные значения:

Оба числовых ряда расходятся, т. к. не выполнен необходимый признак сходимости.
Ответ: ряд сходится на интервале ![]() , сумма ряда:
, сумма ряда: ![]() .
.
Если ![]() , то получаем числовой ряд
, то получаем числовой ряд ![]() , сумма которого равна
, сумма которого равна 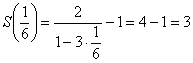
Примечание: также здесь можно использовать формулу суммы бесконечно убывающей геометрической прогрессии:
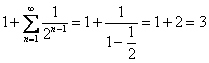
Пример 3. Решение: дифференцируем ряд в его интервале сходимости (на всей числовой прямой) и находим сумму полученного ряда:
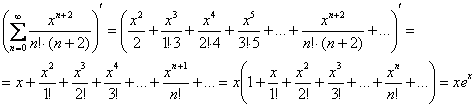
Интегрируем:
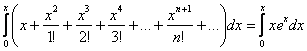
Интеграл правой части берётся по частям:
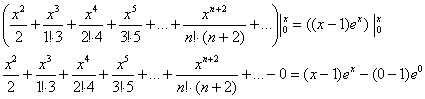
Ответ: ![]() на интервале
на интервале ![]()
Пример 5. Решение: данный ряд сходится в области ![]() . Ориентируясь на разложение
. Ориентируясь на разложение ![]() , выполним следующие преобразования:
, выполним следующие преобразования:

Вычислим сумму ряда в точке ![]()
Ответ: 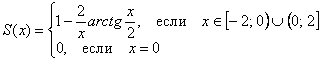
Способ второй: данный ряд сходится в области ![]() . Вычислим его сумму в середине
. Вычислим его сумму в середине ![]() и выполним следующее преобразование:
и выполним следующее преобразование:
![]()
Дифференцируем полученный ряд:

Примечание: использовали разложение ![]() для
для ![]() .
.
Интегрируем:
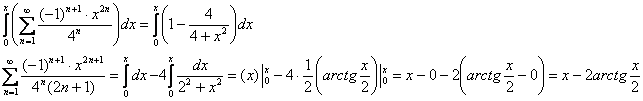
Таким образом:
![]()
Ответ: 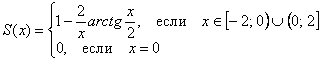
Пример 7. Решение: данный ряд сходится на интервале ![]() .
.
Разделим его на 2 части:
![]()
1) Найдём сумму ![]()
Поскольку «икс» оказался в знаменателе, то контролируем точку ![]() , в которой сумма ряда:
, в которой сумма ряда: ![]() .
.
Интегрируем ряд почленно:

Дифференцируем:
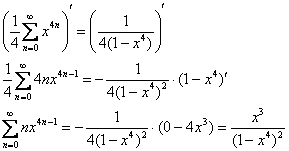
Таким образом:
![]()
2) Найдём сумму ![]()
В результате итоговая сумма:
![]() на всём интервале сходимости, за исключением нуля.
на всём интервале сходимости, за исключением нуля.
Ответ: ![]() на интервалах
на интервалах ![]() и
и ![]() при
при ![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта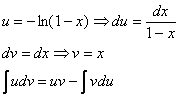


 © Copyright
© Copyright