Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Линии на комплексной плоскости.
Параметрически заданные линии

Казалось бы, при чём здесь х, у…

Этот урок будет полезен не только адептам комплексного анализа, но и всем, кто хочет более подробно ознакомиться с линиями, заданными параметрически, до коих-таки дошли ноги.

Как можно задать линию на комплексной плоскости? Во время построения различных комплексных областей мы естественным образом присоединяли к комплексной плоскости декартову систему координат  и записывали уравнения линий «по-школьному», например,  и так далее:

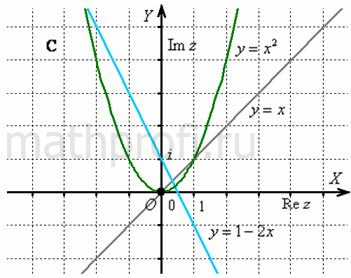
Этот способ прост и широко используется на практике. Однако в некоторых случаях более удобен другой вариант, а именно параметрическое задание линии: . Как вариант, линию можно записать двумя параметрическими уравнениями: , где значениям «тэ» соответствуют различные точки  плоскости .

Параметр «тэ» можно ассоциировать с временем: он непрерывно изменятся от «минус» до «плюс» бесконечности , при этом каждому допустимому значению «тэ» соответствует определённая точки комплексной плоскости. Образно говоря, изменяясь, параметр «вычерчивает» линию.

Так, прямая , очевидно, запишется уравнением , прямая   – в виде , а парабола  – так: .

Следует заметить, что «икс» и «игрек» равноценны, в частности, вместо  можно рассмотреть  и эквивалентное уравнение , которое будет «прочерчивать» ту же самую линию, что и  (с точностью до значений параметра).

Уравнение вида  задаёт окружность с центром в начале координат радиуса «а». Оно следует из элементарных геометрических соображений и легко проверяется аналитически. В самом деле, подставим  и  в декартово уравнение  этой окружности:

и, в силу основного тригонометрического тождества:
 – верное равенство, таким образом, любая точка  удовлетворяет уравнению .

При этом для вычерчивания окружности достаточно рассмотреть промежуток , ибо синус с косинусом периодичны, и мы будем бесконечно «ездить» по окружности, если «пройдём» все значения . Также обратите внимание на следующую вещь: окружность «прорисовывается» против часовой стрелки. Направление проще всего установить опытным путём, рассмотрев несколько точек по ходу изменения параметра. Так, для единичной окружности   удобно взять значения  и, получив соответствующие точки , сделать вывод о направлении:

Такое направление, как многие знают из курса математики / физики, называют положительным. Однако ничто не мешает рассмотреть убывающий от  до 0 параметр, и тогда окружность «прорисуется» в отрицательном направлении (по часовой стрелке).

Если аргумент косинуса и синуса умножить на число, бОльшее единицы, то результат будет достигнут «быстрее», так уравнение  нарисует нам ту же окружность при изменении параметра «тэ» от нуля до «пи». Если же взять «стандартный» промежуток , то окружность прочертится дважды.

И, наоборот, умножая аргумент на число из интервала от 0 до 1, процесс «замедлится», так, уравнение  задаст лишь верхнюю полуокружность при .

Поэтому всегда смотрИте не только на уравнение линии, но и на пределы изменения параметра в той или иной задаче, особенно, на начальное и конечное значение «тэ».

Тренируемся самостоятельно и ни в коем случае не пропускаем это задание:

Пример 1

Записать в параметрической форме :

а) уравнение действительной положительной полуоси , уравнение мнимой оси ;
б) уравнение линии  двумя способами;
в) канонические уравнения эллипса  и гиперболы  (подсказка: взгляните на основное гиперболическое тождество и график гиперболического косинуса). И напомню на всякий пожарный, что .

Сверяемся с решением в конце урока и переходим к более распространённой на практике задаче. Это обратная задача – когда по параметрическому уравнению , удобнее его записать так: , требуется определить вид линии. И здесь есть два «зеркальных» пути, которые направлены на исключение параметра «тэ»:

1) из 1-го уравнения выразить «тэ» через «икс» и подставить во 2-е уравнение,
2) или из 2-го уравнения выразить «тэ» через «игрек» и подставить в 1-е уравнение.

В обоих случаях получаем декартово уравнение  искомой линии, а если повезёт, то функцию  в явном виде:

Пример 2

Определить тип линии:

а) ;

б) ;

в) .

Решаем:
а) Перепишем уравнение  в виде , откуда напрашивается первый путь.

Из 1-го уравнения выражаем  – подставляем во 2-е уравнение :

 – парабола, которую в случае необходимости очень легко построить. А задание, к слову, может требовать от вас ещё и построения чертежа, поэтому я уделю самое пристальное внимание графикам, которые бывают далеко не самыми простыми.

б) Запишем уравнение в виде  и представим его в «алгебраической форме» . Используем формулу Эйлера  для :

и для :
 – используя чётность косинуса и нечётность синуса.

Таким образом:
 или нагляднее
Искомая линия представляет собой эллипс  с полуосями .

Следует заметить, что в вашей задаче может быть предложен конкретный диапазон изменения параметра. Так, пределам  соответствует лишь дуга эллипса в 1-й координатной четверти за исключением, причём, крайней точки .

Ну а если вы позабыли или не знаете, какую линию задают те или иные параметрические уравнения, то можно воспользоваться моим Геометрическим калькулятором (вкладка «Параметрические графики») или онлайн сервисами построения графиков, например, Вольфрамальфа, но должен предупредить – Вольфрам любит начинать отсчёт по осям не с нуля.

в) Расшифруем секанс с тангенсом  и запишем линию в виде .
Из 1-го уравнения даже выражать ничего не надо  – подставляем во 2-е уравнение:
, а вот с синусом повозиться немного придётся.

Из основного тригонометрического тождества  выражаем нужный нам  и из первого уравнения , таким образом:

В результате полученное выше соотношение  запишется в виде:

Возведём обе части в квадрат:

и проведём финальные упрощения:

 – равнобочная гипербола с полуосями  в своём каноническом положении.

Для визуальной проверки результата не помещает «забить» x=2sect и y=2tant в Вольфрамальфа и построить график, ну или мой графопостроитель есть.

Вот так оно бывает, гиперболу, оказывается, можно задать не только гиперболическими косинусом и синусом.

В некоторых примерах может получиться линия более высокого порядка (3-го, 4-го или даже выше) и тогда достаточно дать общий ответ, а-ля « – линия 4-го порядка», если вы конечно не супер-пупер знаток этих линий. Кстати, её и начертить тоже можно с помощью той же вольфрамки – с целью проверки соответствующего параметрического графика или просто ради исследовательского интереса.

Аналогичное задание для самостоятельного решения, самое интересное выбрал :)

Пример 3

Определить тип линии:

а) , не так-то всё тут просто;
б) ;
в)  и пункт на размышления:
г)  – для матёрых ТФКП-нистов.

Думаем (!), решаем, сверяемся (не помешает чертёж в Вольфрамке), разбираемся и продолжаем мучить области и иже с ними границы, отображая их с помощью функций.

Решения и ответы:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте