Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Как найти область определения функции?
Примеры решений

Если где-то нет чего-то, значит, где-то что-то есть

Продолжаем изучение раздела «Функции и графики», и следующая станция нашего путешествия – Область определения функции. Активное обсуждение данного понятия началось в статье о множествах и продолжилось на первом уроке о графиках функций, где я рассмотрел элементарные функции, и, в частности, их области определения. Поэтому чайникам рекомендую начать с азов темы, поскольку я не буду вновь останавливаться на некоторых базовых моментах.

Предполагается, читатель знает область определения следующих функций: линейной, квадратичной, кубической функции, многочленов, экспоненты, синуса, косинуса. Они определены на (множестве всех действительных чисел). За тангенсы, арксинусы, так и быть, прощаю =) – более редкие графики запоминаются далеко не сразу.

Область определения – вроде бы вещь простая, и возникает закономерный вопрос, о чём же будет статья? На данном уроке я рассмотрю распространённые задачи на нахождение области определения функции. Кроме того, мы повторим неравенства с одной переменной, навыки решения которых потребуются и в других задачах высшей математики. Материал, к слову, весь школьный, поэтому будет полезен не только студентам, но и учащимся. Информация, конечно, не претендует на энциклопедичность, но зато здесь не надуманные «мёртвые» примеры, а жареные каштаны, которые взяты из настоящих практических работ.

Начнём с экспресс-вруба в тему. Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс», для которых существуют значения «игреков». Рассмотрим условный пример:

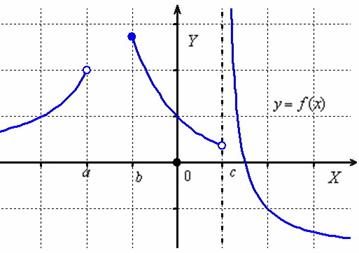
Область определения данной функции представляет собой объединение промежутков:
 (для тех, кто позабыл:  – значок объединения). Иными словами, если взять любое значение «икс» из интервала , или из , или из , то для каждого такого «икс» будет существовать значение «игрек».

Грубо говоря, где область определения – там есть график функции. А вот полуинтервал  и точка «цэ» не входят в область определения и графика там нет.

Да, кстати, если что-нибудь не понятно из терминологии и/или содержания первых абзацев, таки лучше вернуться к статьям Множества и действия над ними, Графики и свойства элементарных функций.

Как найти область определения функции? Многие помнят детскую считалку: «камень, ножницы, бумага», и в данном случае её можно смело перефразировать: «корень, дробь и логарифм». Таким образом, если вам на жизненном пути встречается дробь, корень или логарифм, то следует сразу же очень и очень насторожиться! Намного реже встречаются тангенс, котангенс, арксинус, арккосинус, и о них мы тоже поговорим. Но сначала зарисовки из жизни муравьёв:

Область определения функции, в которой есть дробь

Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.

Не буду останавливаться на самых простых функциях вроде   и т. п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:

Пример 1

Найти область определения функции

Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:

Полученное уравнение имеет два корня: . Данные значения не входят в область определения функции. Действительно, подставьте  или  в функцию  и вы увидите, что знаменатель обращается в ноль.

Ответ: область определения:

Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений ». Напоминаю, что значок обратного слеша в математике обозначает логическое вычитание, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:

Кому как нравится.

В точках  функция терпит бесконечные разрывы, а прямые, заданные уравнениями  являются вертикальными асимптотами для графика данной функции. Впрочем, это уже немного другая тема, и далее я на этом не буду особо заострять внимание.

Пример 2

Найти область определения функции

Задание, по существу, устное и многие из вас практически сразу найдут область определения. Ответ в конце урока.

Всегда ли дробь будет «нехорошей»? Нет. Например, функция  определена на всей числовой оси. Какое бы значение «икс» мы не взяли, знаменатель не обратится в ноль, более того, будет всегда положителен: . Таким образом, область определения данной функции: .

Рекомендую запомнить, при любом значении «икс» и положительной константе :
 

Все функции наподобие  определены и непрерывны на .

Чуть более сложнА ситуация, когда знаменатель оккупировал квадратный трёхчлен:

Пример 3

Найти область определения функции

Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:

Дискриминант получился отрицательным, а значит, действительных корней нет, и наша функция определена на всей числовой оси.

Ответ: область определения:

Пример 4

Найти область определения функции

Это пример для самостоятельного решения. Решение и ответ в конце урока. Советую не лениться с простыми задачками, поскольку к дальнейшим примерам накопится недопонимание.

Область определения функции с корнем

Функция с квадратным корнем  определена только при тех значениях «икс», когда подкоренное выражение неотрицательно: . Если корень расположился в знаменателе , то условие очевидным образом ужесточается: . Аналогичные выкладки справедливы для любого корня положительной чётной степени: , правда, корень уже 4-й степени в исследованиях функций не припоминаю.

Пример 5

Найти область определения функции

Решение: подкоренное выражение должно быть неотрицательным:

Прежде чем продолжить решение, напомню основные правила работы с  неравенствами, известные ещё со школы.

Обращаю особое внимание! Сейчас рассматриваются неравенства с одной переменной – то есть для нас существует только одна размерность по оси . Пожалуйста, не путайте с неравенствами двух переменных, где геометрически задействована вся координатная плоскость. Однако есть и приятные совпадения! Итак, для неравенства равносильны следующие преобразования:

1) Слагаемые можно переносить из части в часть, меняя у них (слагаемых) знаки.

2) Обе части неравенства можно умножить на положительное число.

3) Если обе части неравенства умножить на отрицательное число, то необходимо сменить знак самого неравенства. Например, если было «больше», то станет «меньше»; если было «меньше либо равно», то станет «больше либо равно».

В неравенстве  перенесём «тройку» в правую часть со сменой знака (правило № 1):

Умножим обе части неравенства на –1 (правило № 3):

Умножим обе части неравенства на  (правило № 2):

Ответ: область определения:

Ответ также можно записать эквивалентной фразой: «функция определена при ».
Геометрически область определения изображается штриховкой соответствующих интервалов на оси абсцисс. В данном случае:

Ещё раз напоминаю геометрический смысл области определения – график функции  существует только на заштрихованном участке и отсутствует при .

В большинстве случаев годится чисто аналитическое нахождение области определения, но когда функция сильно заморочена, следует чертить ось  и делать пометки.

Пример 6

Найти область определения функции

Это пример для самостоятельного решения.

Когда под квадратным корнем находится квадратный двучлен или трёхчлен, ситуация немного усложняется, и сейчас мы подробно разберём технику решения:

Пример 7

Найти область определения функции

Решение: подкоренное выражение должно быть строго положительным, то есть нам необходимо решить неравенство . На первом шаге пытаемся разложить квадратный трёхчлен на множители:

Дискриминант положителен, ищем корни:

Таким образом, парабола  пересекает ось абсцисс в двух точках, а это значит, что часть параболы расположена ниже оси (неравенство ), а часть параболы – выше оси (нужное нам неравенство ).

Поскольку коэффициент , то ветви параболы смотрят вверх. Из вышесказанного следует, что на интервалах  выполнено неравенство  (ветки параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке  ниже оси абсцисс, что соответствует неравенству :

! Примечание: если вам не до конца понятны объяснения, пожалуйста, начертите вторую ось и параболу целиком! Целесообразно вернуться к статье Графики и свойства элементарных функций и методичке Горячие формулы школьного курса математики.

Обратите внимание, что сами точки  выколоты (не входят в решение), поскольку неравенство у нас строгое.

Ответ: область определения:

Вообще, многие неравенства (в том числе рассмотренное) решаются универсальным методом интервалов, известным опять же из школьной программы. Но в случаях квадратных дву- и трёхчленов, на мой взгляд, гораздо удобнее и быстрее проанализировать расположение параболы относительно оси . А основной способ – метод интервалов мы детально разберём в статье Нули функции. Интервалы знакопостоянства.

Пример 8

Найти область определения функции

Это пример для самостоятельного решения. В образце подробно закомментирована логика рассуждений + второй способ решения и ещё одно важное преобразование неравенства, без знания которого студент будет хромать на одну ногу…, …хмм… на счёт ноги, пожалуй, погорячился, скорее – на один палец. Большой палец.

Может ли функция с квадратным корнем быть определена на всей числовой прямой? Конечно. Знакомые всё лица: . Или аналогичная сумма с экспонентой: . Действительно, для любых значения «икс» и «ка»: , поэтому подАвно и .

А вот менее очевидный пример: . Здесь дискриминант отрицателен (парабола не пересекает ось абсцисс), при этом ветви параболы направлены вверх, следовательно,  и область определения: .

Вопрос противоположный: может ли область определения функции быть пустой? Да, и сразу напрашивается примитивный пример , где подкоренное выражение отрицательно при любом значении «икс», и область определения:  (значок пустого множества). Такая функция не определена вообще (разумеется, график тоже иллюзорен).

С нечётными корнями   и т. д. всё обстоит гораздо лучше – тут подкоренное выражение может быть и отрицательным. Например, функция  определена на всей числовой прямой. Однако у функции  единственная точка  всё же не входит в область определения, поскольку обращают знаменатель в ноль. По той же причине для функции  исключаются точки .

Некоторым посетителям сайта рассматриваемые примеры покажутся элементарными и примитивными, но в этом нет случайности – во-первых, я стараюсь «заточить» материал для нубов, а во-вторых, подбираю реалистичные вещи под грядущие задачи: полное исследование функции, нахождение области определения функции двух переменных и некоторые другие. Всё в математике цепляется друг за дружку. Хотя любители трудностей тоже не останутся обделёнными, более солидные задания встретятся и здесь, и на уроке
о методе интервалов.

Область определения функции с логарифмом

Третья распространённая функция – логарифм. В качестве образца я буду рисовать натуральный логарифм, который попадается примерно в 99 примерах из 100. Если некоторая функция содержит логарифм , то в её область определения должны входить только те значения «икс», которые удовлетворяют неравенству . Если логарифм находится в знаменателе: , то дополнительно накладывается условие  (так как ).

Пример 9

Найти область определения функции

Решение: в соответствии с вышесказанным составим и решим систему:

Графическое решение для чайников:

Ответ: область определения:

Остановлюсь ещё на одном техническом моменте – у меня ведь не указан масштаб и не проставлены деления по оси. Возникает вопрос: как выполнять подобные чертежи в тетради на клетчатой бумаге? Отмерять ли расстояние между точками по клеточкам строго по масштабу? Каноничнее и строже, конечно, масштабировать, но вполне допустим и схематический чертёж, принципиально отражающий ситуацию.

Пример 10

Найти область определения функции

Для решения задачи можно использовать метод предыдущего параграфа – проанализировать, как парабола расположена относительно оси абсцисс. Ответ в конце урока.

Как видите, в царстве логарифмов всё очень похоже на ситуацию с квадратным корнем: функция  (квадратный трёхчлен из Примера № 7) определена на интервалах , а функция  (квадратный двучлен из Примера № 8) на интервале . Неловко уже и говорить, функции типа  определены на всей числовой прямой.

Полезная информация: интересна типовая функция , она определена на всей числовой прямой кроме точки . Согласно свойству логарифма , «двойку» можно вынести множителем за пределы логарифма, но, чтобы функция не изменилась, «икс» нужно заключить под знак модуля: . Вот вам и ещё одно «практическое применение» модуля = ). Так следует поступать в большинстве случаев, когда вы снОсите чётную степень, например: .  Если же основание степени  заведомо положительно, например, , то в знаке модуля надобность отпадает и достаточно обойтись круглыми скобками: .

Чтобы не повторяться, давайте усложним задание:

Пример 11

Найти область определения функции

Решение: в данной функции у нас присутствует и корень и логарифм.

Подкоренное выражение должно быть неотрицательным: , а выражение под знаком логарифма – строго положительным: . Таким образом, нужно решить систему:

Многие из вас прекрасно знают или интуитивно догадываются, что решение системы должно удовлетворять каждому условию.

Исследуя расположение параболы  относительно оси , приходим к выводу, что неравенству  удовлетворяет интервал  (синяя штриховка):

Неравенству , очевидно, соответствует «красный» полуинтервал  .

Поскольку оба условия должны выполняться одновременно, то решением системы является пересечение данных интервалов. «Общие интересы» соблюдены на полуинтервале .

Ответ: область определения:

Типовое неравенство , как демонстрировалось в Примере № 8,  нетрудно разрешить и аналитически.

Найденная область определения не изменится для «похожих функций», например, для  или .  Также можно добавить какие-нибудь непрерывные на  функции, например: , или так: , или даже так: . Как говорится, корень и логарифм – вещь упрямая. Единственное, если одну из функций «сбросить» в знаменатель, то область определения изменится (хотя в общем случае это не всегда справедливо). Ну а в теории матана по поводу этого словесного… ой… существуют теоремы.

Пример 12

Найти область определения функции

Это пример для самостоятельного решения. Использование чертежа вполне уместно, так как функция не самая простая.

Ещё пару примеров для закрепления материала:

Пример 13

Найти область определения функции

Решение: составим и решим систему:

Все действия уже разобраны по ходу статьи. Изобразим на числовой прямой интервал, соответствующий неравенству  и, согласно второму условию, исключим две точки:

Значение  оказалось вообще не при делах.

Ответ: область определения

Небольшой математический каламбур на вариацию 13-го примера:

Пример 14

Найти область определения функции

Это пример для самостоятельного решения. Кто пропустил, тот в пролёте ;-)

Завершающий раздел урока посвящен более редким, но тоже «рабочим» функциям:

Области определения функций
с тангенсами, котангенсами, арксинусами, арккосинусами

Перед изучением параграфа рекомендую вновь вернуться к первой статье о графиках, чтобы освежить визуальную и аналитическую информацию о перечисленных в заголовке функциях.

Если в некоторую функцию входит , то из её области определения исключаются точки , где Z –  множество целых чисел. В частности, как отмечалось в статье Графики и свойства элементарных функций, у функции  выколоты следующие значения:

То есть, область определения тангенса: .

Убиваться сильно не будем:

Пример 15

Найти область определения функции

Решение: в данном случае  и в область определения не войдут следующие точки:

Скинем «двойку» левой части в знаменатель правой части:

В результате :

Ответ: область определения: .

В принципе, ответ можно записать и в виде объединения бесконечного количества интервалов, но конструкция получится весьма громоздкой:

Аналитическое решение полностью согласуется с геометрическим преобразованием графика: если аргумент функции умножить на 2, то её график сожмётся к оси  в два раза. Заметьте, как у функции  уполовинился период, и точки разрыва участились в два раза. Тахикардия.

Похожая история с котангенсом. Если в некоторую функцию входит , то из её области определения исключаются точки . В частности, для функции  автоматной очередью расстреливаем следующие значения:

Иными словами:

Миниатюра для самостоятельного решения:

Пример 16

Найти область определения функции

Арксинус с арккосинусом, как всегда, выступают хедлайнером математического концерта, и этого стоило дождаться, поскольку кроме нахождения области определения вы сможете научиться решать двойные неравенства (или повторить их).

Если в некоторую функцию входит  или , то на её область определения накладывается ограничение в виде двойного неравенства: .

Пример 17

Найти область определения функции

Решение: составим двойное неравенство:

Действия с двойным неравенством очень похожи на действия с «обычным» одинарным неравенством. Конечная цель преобразований – добиться, чтобы в середине остался только «икс».

Сначала избавимся в средней части от константы, для этого вычтем из каждой части неравенства «тройку»:

Умножим все три части неравенства на –1. Поскольку множитель отрицателен, то знаки самих неравенств необходимо «развернуть» в противоположную сторону:

Умножим все части неравенства на :

Запишем ответ, переставив знаки неравенств в привычном порядке, а то по-арабски как-то получилось – от «единицы» до «двух» справа налево.

Ответ: область определения:  или

Несложный заключительный пример для самостоятельного решения:

Пример 18

Найти область определения функции

Хотелось разобрать более трудные примеры со сложными функциями когда, скажем, под квадратный корень вложена дробь или логарифм, но для этого нужно рассказывать про метод интервалов, который сейчас наверняка запутает значительную часть аудитории. В этой связи я решил перенести объяснения на урок о нулях и интервалах знакопостоянства функции, где постараюсь вернуться к нахождению области определения сложных функций. А на данный момент лучше усвоить меньше, да качественнее!

Желаю успехов!

Решения и ответы:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте