


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Эффективные методы решения
определенных и несобственных интегралов
Данная статья содержит дополнительные материалы по методам решения определенных и несобственных интегралов. Предполагается, что читатель владеет средними или высокими навыками интегрирования. Если это не так, пожалуйста, начните с азов, предназначенных для чайников: Неопределенный интеграл, примеры решений.
Где неопределенный интеграл – там неподалёку и Определенный интеграл, с формулой Ньютона-Лейбница вы тоже должны быть знакомы не понаслышке. Кроме того, уметь решать простейшие задачи на вычисление площади плоской фигуры.
Урок предназначен для тех, кто хочет научиться быстрее и эффективнее решать определенные и несобственные интегралы. Сначала я рассмотрю особенности интегрирования четной и нечетной функции по симметричному относительно нуля промежутку. Затем мы разберем задачу о нахождении площади круга с помощью определенного интеграла. Эта задача важна еще и тем, что знакомит вас с распространенным приемом интегрирования определенного интеграла – тригонометрической подстановкой. Она еще нигде не рассматривалась – новый материал!
Второй раздел предназначен для читателей, знакомых с несобственными интегралами. Аналогично, рассмотрим несобственные интегралы от четных, нечетных функций по симметричному интервалу. В том числе более редкие типы несобственных интегралов, которые не вошли в основную статью: когда нижний предел стремится к «минус бесконечности», когда оба предела стремятся к бесконечности, когда в обоих концах отрезка интегрирования функция терпит бесконечный разрыв (это уже интеграл второго рода). И совсем редкий несобственный интеграл – с точкой разрыва на отрезке интегрирования.
Если вам интересно что-то конкретное, сразу ссылки:
- Определённый интеграл от чётной функции по симметричному отрезку
- Вычисление площади круга, тригонометрическая подстановка
- Определённые интегралы от нечётных функций
- Несобственный интеграл с бесконечным нижним пределом
- Несобственные интегралы с бесконечными пределами интегрирования
- Несобственный интеграл 2-го рода с разрывами на обоих концах отрезка
- Несобственные интегралы с разрывом на отрезке интегрирования
Метод решения определенного интеграла от четной функции
по симметричному относительно нуля отрезку
Рассмотрим определенный интеграл вида  . Легко заметить, что отрезок интегрирования
. Легко заметить, что отрезок интегрирования ![]() симметричен относительно нуля.
симметричен относительно нуля.
Если функция подынтегральная ![]() является чётной, то интеграл
является чётной, то интеграл  можно вычислить по половине отрезка, а результат – удвоить:
можно вычислить по половине отрезка, а результат – удвоить:  .
.
Многие догадались, почему так, тем не менее, рассмотрим конкретный пример с чертежом:
Пример 1
Вычислить определенный интеграл![]()
О чётности функции много говорилось в методическом материале Графики и свойства элементарных функций. Повторим один раз: функция является чётной, если для неё выполняется равенство ![]() . Как проверить функцию на чётность? Нужно вместо «икс» подставить
. Как проверить функцию на чётность? Нужно вместо «икс» подставить ![]() .
.
В данном случае: ![]()
![]() , значит, данная функция является чётной.
, значит, данная функция является чётной.
Согласно правилу, на симметричном относительно нуля отрезке ![]() наш интеграл от чётной функции можно вычислить следующим образом:
наш интеграл от чётной функции можно вычислить следующим образом:

А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу….
Любая чётная функция, в частности ![]() , симметрична относительно оси
, симметрична относительно оси ![]() :
:
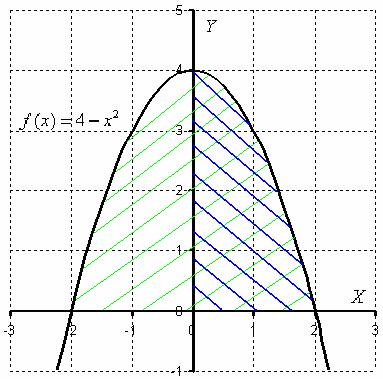
Определенный интеграл ![]() численно равен площади плоской фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а значит, симметричности её графика относительно оси
численно равен площади плоской фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а значит, симметричности её графика относительно оси ![]() , достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые же половинки!
, достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые же половинки!
Именно поэтому справедливо действие 
Аналогичная история происходит с любой чётной функцией ![]() по симметричному относительно нуля отрезку:
по симметричному относительно нуля отрезку:

Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим:

Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Замечу, что это еще был простой демонстрационный пример, на практике всё бывает хуже.
Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает.
Короткий разминочный пример для самостоятельного решения:
Пример 2
Вычислить определенный интеграл![]()
Полное решение и ответ в конце урока.
Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Иллюстрация к Примеру 1 дана только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка:
Пример 3
1) Вычислить определенный интеграл  .
.
2) Вычислить площадь плоской фигуры, ограниченной линиями ![]() и осью
и осью ![]() на интервале
на интервале ![]() .
.
Это две разные задачи! Об этом уже говорилось в статье Как вычислить площадь плоской фигуры? Сначала разберемся с первым пунктом:
1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:

Определенный интеграл получился отрицательным и так бывает!
2) Теперь найдем площадь плоской фигуры. Вот здесь без чертежа обойтись трудно:
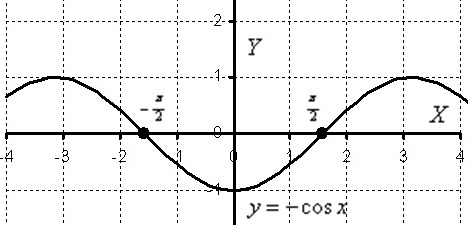
Если у вас возникло затруднение с наивным косинусом, пожалуйста, обратитесь к статье Геометрические преобразования графиков.
На отрезке ![]() график функции расположен ниже оси
график функции расположен ниже оси ![]() , поэтому:
, поэтому:

Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (также см. пример 3 урока Определенный интеграл. Как вычислить площадь фигуры).
Заметьте, что чётность косинуса никто не отменял, поэтому мы опять споловинили отрезок, и удвоили интеграл.
Вычисление площади круга с помощью определенного интеграла
Тригонометрическая подстановка
Это очень важная задача, поскольку будет рассмотрен типовой интеграл и приём решения, который неоднократно встретится в будущем.
Но сначала небольшое напоминание по уравнению окружности. Уравнение вида ![]() задаёт окружность с центром в точке
задаёт окружность с центром в точке ![]() радиуса
радиуса ![]() . В частности, уравнение
. В частности, уравнение ![]() задаёт окружность радиуса
задаёт окружность радиуса ![]() с центром в начале координат.
с центром в начале координат.
Пример 4
Вычислить площадь круга, ограниченного окружностью, заданной уравнением ![]()
![]() – это окружность с центром в начале координат радиуса
– это окружность с центром в начале координат радиуса ![]() .
.
Выполним чертёж:
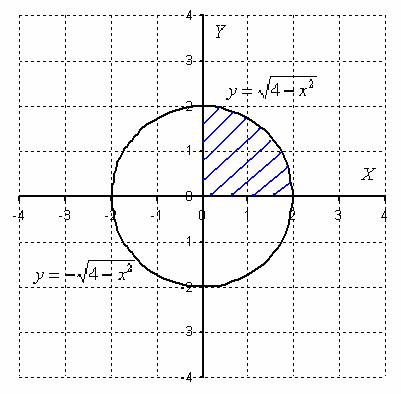
Сначала вычислим площадь круга с помощью известной школьной формулы. Если радиус круга ![]() , то его площадь равна:
, то его площадь равна: ![]()
Для того чтобы вычислить площадь круга с помощью определенного интеграла, необходимо из уравнения окружности ![]() выразить функцию «игрек» в явном виде:
выразить функцию «игрек» в явном виде:
![]()
Верхняя полуокружность задается уравнением ![]()
Нижняя полуокружность задается уравнением ![]()
Особые параноики, как я, могут подставить несколько точек окружности в эти уравнения, и убедиться в справедливости вышеизложенных утверждений.
Как вычислить площадь круга? В данном примере круг симметричен относительно начала координат, поэтому достаточно вычислить площадь сектора в 1-й четверти (заштрихован синим цветом), затем результат умножить на 4.
Таким образом:

Такой же, но неопределенный интеграл рассматривался в примере 6 урока Сложные интегралы, он решался длительным и трудоёмким методом сведения интеграла к самому себе. Можно пойти тем же путём, но для определенного интеграла существует удобный и эффективный метод тригонометрической замены:
Проведём замену: ![]()
Почему именно такая замена, очень скоро станет понятно, а пока найдем дифференциал:
![]()
Выясним, во что превратится корень, я распишу очень подробно:
![]()
Если в ходе решения вы не сможете догадаться применить формулу наподобие ![]() , то, увы, схлопочете от преподавателя «приходите в следующий раз».
, то, увы, схлопочете от преподавателя «приходите в следующий раз».
После преобразования корня отчетливо видно, почему проведена замена ![]() , особое внимание обращаю на коэффициент при синусе – «двойке», этот коэффициент нужно подбирать таким образом, чтобы при возведении в квадрат всё хорошо вынеслось за скобки и из-под корня.
, особое внимание обращаю на коэффициент при синусе – «двойке», этот коэффициент нужно подбирать таким образом, чтобы при возведении в квадрат всё хорошо вынеслось за скобки и из-под корня.
Осталось вычислить новые пределы интегрирования:
Если ![]() , то
, то ![]()
Новый нижний предел интегрирования: ![]()
Новый верхний предел интегрирования: ![]()
Таким образом:

Площадь сектора необходимо умножить на 4, следовательно, площадь всей окружности:
![]()
Вероятно, у некоторых возник вопрос, зачем вообще мучиться с интегралом, если есть короткая школьная формула ![]() ? А фишка состоит в том, что возможность очень точно вычислить площадь круга появилась только с развитием математического анализа (хотя уже в древности площадь круга рассчитывали с приличной точностью).
? А фишка состоит в том, что возможность очень точно вычислить площадь круга появилась только с развитием математического анализа (хотя уже в древности площадь круга рассчитывали с приличной точностью).
Разобранный пример можно решить в общем виде, то есть найти площадь круга, ограниченного окружностью произвольного радиуса: ![]() . В результате получится как раз формула
. В результате получится как раз формула ![]() !
!
Следует отметить, что к решению данной задачи можно было применить и другой подход – вычислить площадь верхнего полукруга с помощью интеграла ![]() , а затем удвоить результат. Но в силу чётности подынтегральной функции решение элементарно сводится к оптимальной версии:
, а затем удвоить результат. Но в силу чётности подынтегральной функции решение элементарно сводится к оптимальной версии:

Еще раз подчёркиваю важность проведенной тригонометрической замены, она встретится на практике ни раз и ни два. Поэтому для закрепления материала чуть более сложное задание для самостоятельного решения:
Пример 5
Вычислить определенный интеграл
По условию требуется вычислить определенный интеграл, поэтому чертеж выполнять не нужно. Хорошо подумайте над коэффициентом в замене ![]() . Если возникнут трудности с интегралом после замены, вернитесь к уроку Интегралы от тригонометрических функций. Будьте внимательны! Полное решение и ответ в конце урока.
. Если возникнут трудности с интегралом после замены, вернитесь к уроку Интегралы от тригонометрических функций. Будьте внимательны! Полное решение и ответ в конце урока.
Метод решения определенного интеграла от нечетной функции
по симметричному относительно нуля отрезку
Вам понравится.
Рассмотрим тот же определенный интеграл с симметричным относительно нуля отрезком интегрирования:  .
.
Если подынтегральная функция ![]() является нечётной, то
является нечётной, то  .
.
Почему такой интеграл равен нулю?
Пример 6
Вычислить определенный интеграл![]()
Выполним чертеж:

Вот, заодно и график функции ![]() , который ещё нигде у меня не встречался, график представляет собой перевёрнутую кубическую параболу.
, который ещё нигде у меня не встречался, график представляет собой перевёрнутую кубическую параболу.
Проверим нашу функцию на четность/нечетность:
![]() , значит, данная функция является нечётной, и её график симметричен относительно начала координат. Из симметрии графика следует равенство площадей, которые заштрихованы красным и синим цветом.
, значит, данная функция является нечётной, и её график симметричен относительно начала координат. Из симметрии графика следует равенство площадей, которые заштрихованы красным и синим цветом.
При вычислении определенного интеграла ![]() площадь, которая заштрихована синим цветом, формально является отрицательной. А площадь, которая заштрихована красным цветом – положительной. Поскольку площади равны и формально противоположны по знаку, то они взаимно уничтожаются, следовательно
площадь, которая заштрихована синим цветом, формально является отрицательной. А площадь, которая заштрихована красным цветом – положительной. Поскольку площади равны и формально противоположны по знаку, то они взаимно уничтожаются, следовательно ![]() .
.
И еще раз подчеркиваю разницу между заданиями:
1) Любой определенный интеграл (само собой он должен существовать) – это всё равно формально площадь (пусть даже отрицательная). В частности, поэтому  , так как в силу нечётности функции
, так как в силу нечётности функции ![]() площади взаимно уничтожатся. Что и проиллюстрировано на конкретном примере.
площади взаимно уничтожатся. Что и проиллюстрировано на конкретном примере.
2) Задача на нахождение площади – это совершенно другая задача. Так, если бы нам было предложено найти площадь фигуры в данном примере, то её следовало бы вычислить следующим образом: 
Еще несколько коротких примеров на тему данного правила:

И, аналогично для любой нечетной функции и симметричного относительно нуля отрезка.
Применять ли данный метод на практике? На самом деле вопрос не такой простой. Когда вам предложен сложный пример с большим количеством вычислений, то можно, и даже уместно указать, что такой интеграл равен нулю, сославшись на нечетность функции и симметричность отрезка интегрирования относительно нуля. Как говорится, знание – сила, а незнание – рабочая сила.
Но когда вам предложен короткий пример, то преподаватель вполне обоснованно может заставить прорешать его подробно: взять интеграл и подставить пределы интегрирования по формуле Ньютона-Лейбница. Например, вам предложено вычислить тот же определенный интеграл ![]() . Если вы сразу запишите, что
. Если вы сразу запишите, что ![]() и поясните словами, почему получается ноль, то это будет не очень хорошо. Намного лучше «прикинуться дурачком» и провести полное решение:
и поясните словами, почему получается ноль, то это будет не очень хорошо. Намного лучше «прикинуться дурачком» и провести полное решение:
![]()
А то, что интеграл равен нулю, вы будете знать заранее ;-) И это знание 100%-но позволит избежать ошибки.
Метод решения несобственного интеграла с бесконечным нижним пределом
Второй раздел статьи предназначен для тех, кто хорошо разобрался с уроком Несобственные интегралы. Примеры решения, или, по крайне мере, понял бОльшую его часть. Речь пойдет о несобственных интегралах первого рода с бесконечным нижним пределом: ![]() .
.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
![]()
Чем отличается данный интеграл от «обычного» несобственного интеграла с бесконечным верхним пределом? По технике решения практически ничем. Так же нужно найти первообразную (неопределенный интеграл), так же нужно использовать предел при вычислении интеграла. Отличие состоит в том, что необходимо устремить нижний предел интегрирования к «минус бесконечности»: ![]() .
.
Из вышесказанного следует очевидная формула для вычисления такого несобственного интеграла:
![]()
В данном примере, подынтегральная функция непрерывна на ![]() и:
и:
![]() , то есть, несобственный интеграл расходится.
, то есть, несобственный интеграл расходится.
Вот тут, главное, быть аккуратным в знаках, и не забывать, что ![]() . Нужно внимательно разобраться, что куда стремится.
. Нужно внимательно разобраться, что куда стремится.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Метод решения несобственного интеграла
с бесконечными пределами интегрирования
Очень интересный случай. Несобственный интеграл первого рода с бесконечными пределами интегрирования имеет следующий вид:
![]()
Как его решить? Данный интеграл нужно представить в виде суммы двух несобственных интегралов:
 (всё гениальное просто) и смотреть по ситуации:
(всё гениальное просто) и смотреть по ситуации:
Примечание: вместо ноля может быть любое число, но ноль обычно удобнее всего.
Пример 9
Вычислить несобственный интеграл или установить его расходимость.
![]()
Подынтегральная функция непрерывна на всей числовой прямой. Представляем интеграл в виде суммы двух интегралов:

и разделываемся с ними по отдельности:
![]()

Таким образом:
![]() , то есть несобственный интеграл существует и сходится.
, то есть несобственный интеграл существует и сходится.
Теперь обратим внимание на подынтегральную функцию. Она является чётной.
В несобственных интегралах с бесконечными пределами (а значит, симметричным интервалом интегрирования) чётностью пользоваться МОЖНО. Аналогично определенному интегралу, промежуток выгодно споловинить, а результат – удвоить:

Почему такое возможно? График подынтегральной чётной функции симметричен относительно оси ![]() . Следовательно, если половина площади конечна (интеграл сходится) – то симметричная половина площади тоже конечна. Если половина площади бесконечна (интеграл расходится), следовательно, симметричная половина тоже будет расходиться. И не забываем о третьем случае: если половины не существует, то второй, и всего интеграла – тоже. Например:
. Следовательно, если половина площади конечна (интеграл сходится) – то симметричная половина площади тоже конечна. Если половина площади бесконечна (интеграл расходится), следовательно, симметричная половина тоже будет расходиться. И не забываем о третьем случае: если половины не существует, то второй, и всего интеграла – тоже. Например:
 – данного предела не существует, а значит, не существует и несобственного интеграла
– данного предела не существует, а значит, не существует и несобственного интеграла ![]() .
.
Переходим ещё к более любопытному случаю:
Пример 10
Исследовать несобственный интеграл на сходимость.
![]()
Обратите внимание на задание – здесь в условии уже не констатируется факт существования интеграла.
Подынтегральная функция непрерывна на всей числовой прямой, и мы в академичном стиле распиливаем пациента на две части:

Решаем первый:
![]()
и второй:

И, несмотря на то, что оба интеграла по отдельности расходятся – итогового интеграла в общем случае не существует, ибо сумма ![]() не определена. Почему? Потому что переменная «а» может стремиться к «минус бесконечности», например, БЫСТРЕЕ, чем переменная «бэ» к «плюс бесконечности» (или наоборот).
не определена. Почему? Потому что переменная «а» может стремиться к «минус бесконечности», например, БЫСТРЕЕ, чем переменная «бэ» к «плюс бесконечности» (или наоборот).
Но существует особый частный случай – когда обе переменные стремятся к бесконечностям одинаково. Это выражается пределом:
![]()
![]() и называется сходимостью интеграла по Коши. Само же значение предела называют главным значением несобственного интеграла.
и называется сходимостью интеграла по Коши. Само же значение предела называют главным значением несобственного интеграла.
И поскольку условие требовало от нас исследования, то здесь будет грамотным следующий ответ: в общем случае несобственного интеграла ![]() не существует, однако имеет место сходимость по Коши и главное значение интеграла равно нулю. Главное значение принято обозначать так:
не существует, однако имеет место сходимость по Коши и главное значение интеграла равно нулю. Главное значение принято обозначать так: ![]()
А сейчас очень важный момент: подынтегральная функция ![]() является нечётной, и как вы правильно догадываетесь, в несобственных интегралах с бесконечными пределами нечётностью пользоваться НЕ СЛЕДУЕТ!!!
является нечётной, и как вы правильно догадываетесь, в несобственных интегралах с бесконечными пределами нечётностью пользоваться НЕ СЛЕДУЕТ!!!
В этом состоит отличие от определенного интеграла. Там можно смело записать, что ![]() , а здесь так поступать не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится автоматическая ошибка
, а здесь так поступать не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится автоматическая ошибка ![]() , что не соответствует действительности.
, что не соответствует действительности.
Тонкость же состоит в том, что интегралы ![]() от некоторых нечётных функций
от некоторых нечётных функций ![]() и в самом деле равны нулю! И как раз этой тонкости посвящен следующий пример для самостоятельного решения:
и в самом деле равны нулю! И как раз этой тонкости посвящен следующий пример для самостоятельного решения:
Пример 11
Вычислить несобственный интеграл или установить его расходимость.
![]()
Полное решение и ответ в конце урока.
Метод решения несобственного интеграла второго рода
с точками разрыва на обоих концах отрезка
Заключительные пункты этой статьи предназначены для читателей, которые хорошо разобрались с несобственными интегралами второго рода на уроке Несобственные интегралы. Примеры решений. Рассмотрим другие разновидности несобственных интегралов второго рода. Ничего сложного!
Многие выкладки предыдущего параграфа будут справедливы и сейчас.
Сразу конкретная задача:
Пример 12
Вычислить несобственный интеграл или установить его расходимость.
![]()
Подынтегральная функция терпит бесконечные разрывы в обоих концах отрезка интегрирования. Изобразим подынтегральную функцию ![]() на чертеже:
на чертеже:
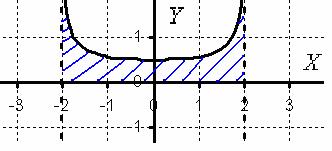
Геометрически данный несобственный интеграл представляет собой площадь бесконечной криволинейной трапеции, которая не ограничена сверху.
Методика решения точно такая же, как и в предыдущем параграфе – разделяй и властвуй:

А уж интегралы правой части рассматривались во втором разделе урока Несобственные интегралы. Примеры решений.
Но, вместо этого замечаем, что подынтегральная функция является чётной. Чётность использовать МОЖНО. В этом легко убедиться и по чертежу. Таким образом, интеграл целесообразно споловинить, а результат удвоить. Решаем наиболее рациональным способом:
![]()
Подынтегральная функция терпит бесконечные разрывы в точках ![]() . Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.
. Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.

Ответ: ![]() , то есть, несобственный интеграл сходится
, то есть, несобственный интеграл сходится
Пример 13
Исследовать несобственный интеграл на сходимость ;)

Это пример для самостоятельного решения. Всё, как и в предыдущем параграфе – нечетностью функции пользоваться НЕ НУЖНО. Аккуратно делим интеграл на две части и исследуем сходимость по типовому алгоритму. Полное решение и ответ в конце урока.
Не редкость, когда подынтегральная функция не является четной или нечетной, да и отрезок интегрирования не симметричен относительно нуля. Например, рассмотрим несобственный интеграл  . Подынтегральная функция опять терпит бесконечные разрывы в обоих концах отрезка интегрирования. Алгоритм такой же, делим интеграл на два интеграла:
. Подынтегральная функция опять терпит бесконечные разрывы в обоих концах отрезка интегрирования. Алгоритм такой же, делим интеграл на два интеграла:

Интегралы правой части разобраны на уроке Несобственные интегралы. Примеры решений. В качестве факультатива выясните, существует ли этот интеграл в общем случае, и если существует – то сходится или нет.
Метод решения несобственного интеграла
с точкой разрыва на отрезке интегрирования
Если честно, такой пример встречался в моей практике всего один раз (по крайне мере, вспомнил лишь один), поэтому я ограничусь только обзором.
Пример опять же будет в известной степени условным, первое, что в голову пришло. Рассмотрим несобственный интеграл  . На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке
. На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке ![]() . Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интегрирования не симметричен относительно нуля.
. Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интегрирования не симметричен относительно нуля.
Метод уже состарился, как хмм… чешуя динозавра. Представим несобственный интеграл в виде суммы двух несобственных интегралов:

Интегралы правой части вам уже знакомы. А проговаривать алгоритм в третий раз не буду, смотрите предыдущие два параграфа)
Желаю успехов!
Решения и ответы:
Пример 2: Решение:

Пример 5: Решение:

Проведем замену:
![]()

Новые пределы интегрирования:


Пример 8: Решение:
![]()
Подынтегральная функция непрерывна на ![]()

Пример 11: Решение:
![]()
Подынтегральная функция непрерывна на всей числовой прямой.
Представим интеграл в виде суммы двух интегралов:

Вычислим первый интеграл:

Вычислим второй интеграл:

Таким образом:
![]() – интеграл сходится и равен нулю.
– интеграл сходится и равен нулю.
Ответ: ![]()
Примечание 1: В частности, равно нулю и главное значение интеграла
Примечание 2: Будет серьезной оплошностью сразу записать, что ![]() , пользуясь нечетностью подынтегральной функции и симметричностью интервала интегрирования. Стандартный алгоритм обязателен!!!
, пользуясь нечетностью подынтегральной функции и симметричностью интервала интегрирования. Стандартный алгоритм обязателен!!!
Пример 13: Решение: 
Подынтегральная функция терпит бесконечные разрывы в точках ![]() .
.
Представим данный интеграл в виде суммы двух интегралов:

Вычислим первый интеграл:

Вычислим второй интеграл:

Таким образом, интеграла  в общем случае не существует. Исследуем сходимость интеграла по Коши, используем чётность косинуса и свойство логарифмов:
в общем случае не существует. Исследуем сходимость интеграла по Коши, используем чётность косинуса и свойство логарифмов:

Ответ: интеграл сходится лишь по Коши, главное значение 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright