


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Непрерывность функции. Точки разрыва.
Как исследовать функцию на непрерывность?
Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!
На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность. Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.
Что нужно знать и уметь? Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции. Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций. Также желательно ознакомиться с геометрическими преобразованиями графиков, поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!
Непрерывность функции. Точки разрыва и их классификация
Понятие непрерывности функции
Рассмотрим некоторую функцию ![]() , непрерывную на всей числовой прямой:
, непрерывную на всей числовой прямой:
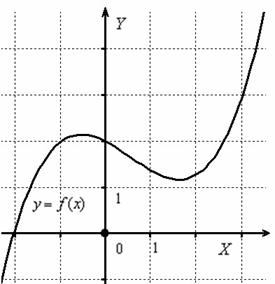
Или, говоря лаконичнее, наша функция непрерывна на ![]() (множестве действительных чисел).
(множестве действительных чисел).
Каков «обывательский» критерий непрерывности? Очевидно, что график непрерывной функции можно начертить, не отрывая карандаша от бумаги.
При этом следует чётко отличать два простых понятия: область определения функции и непрерывность функции. В общем случае это не одно и то же. Например:
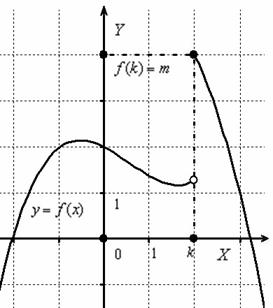
Данная функция определена на всей числовой прямой, то есть для каждого значения «икс» существует своё значение «игрека» ![]() . В частности, если
. В частности, если ![]() , то
, то ![]() . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции:
. Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции: ![]() .
.
Однако эта функция не является непрерывной на ![]() ! Совершенно очевидно, что в точке
! Совершенно очевидно, что в точке ![]() она терпит разрыв. Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги. Немного позже мы рассмотрим классификацию точек разрыва.
она терпит разрыв. Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги. Немного позже мы рассмотрим классификацию точек разрыва.
Непрерывность функции в точке и на интервале
В той или иной математической задаче речь может идти о непрерывности функции в точке, непрерывности функции на интервале, полуинтервале или непрерывности функции на отрезке. То есть, не существует «просто непрерывности» – функция может быть непрерывной ГДЕ-ТО. И основополагающим «кирпичиком» всего остального является непрерывность функции в точке.
Теория математического анализа даёт определение непрерывности функции в точке с помощью «дельта» и «эпсилон» окрестностей, но на практике в ходу другое определение, которому мы и уделим самое пристальное внимание.
Сначала вспомним односторонние пределы, ворвавшиеся в нашу жизнь на первом уроке о графиках функций. Рассмотрим будничную ситуацию:
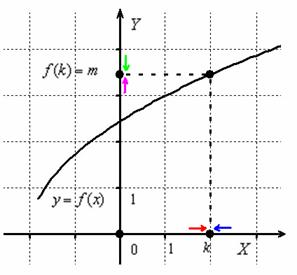
Если приближаться по оси ![]() к точке
к точке ![]() слева (красная стрелка), то соответствующие значения «игреков» будут идти по оси
слева (красная стрелка), то соответствующие значения «игреков» будут идти по оси ![]() к точке
к точке ![]() (малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела:
(малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела:
![]()
Обратите внимание на запись ![]() (читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу
(читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу ![]() с левой стороны.
с левой стороны.
Аналогично, если приближаться к точке «ка» справа (синяя стрелка), то «игреки» придут к тому же значению ![]() , но уже по зелёной стрелке, и правосторонний предел оформится следующим образом:
, но уже по зелёной стрелке, и правосторонний предел оформится следующим образом:
![]()
«Добавка» ![]() символизирует бесконечно малое положительное число, и запись
символизирует бесконечно малое положительное число, и запись ![]() читается так: «икс стремится к ка справа».
читается так: «икс стремится к ка справа».
Если односторонние пределы конечны и равны (как в нашем случае): ![]() , то будем говорить, что существует ОБЩИЙ предел
, то будем говорить, что существует ОБЩИЙ предел ![]() . Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.
. Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.
Заметьте, что если функция не определена при ![]() (выколите чёрную точку на ветке графика), то перечисленные выкладки остаются справедливыми. Как уже неоднократно отмечалось, в частности, в статье о бесконечно малых функциях, выражения
(выколите чёрную точку на ветке графика), то перечисленные выкладки остаются справедливыми. Как уже неоднократно отмечалось, в частности, в статье о бесконечно малых функциях, выражения ![]() означают, что «икс» бесконечно близко приближается к точке
означают, что «икс» бесконечно близко приближается к точке ![]() , при этом НЕ ИМЕЕТ ЗНАЧЕНИЯ, определена ли сама функция в данной точке или нет. Хороший пример встретится в следующем параграфе, когда анализу подвергнется функция
, при этом НЕ ИМЕЕТ ЗНАЧЕНИЯ, определена ли сама функция в данной точке или нет. Хороший пример встретится в следующем параграфе, когда анализу подвергнется функция ![]() .
.
Определение: функция непрерывна в точке ![]() , если предел функции в данной точке равен значению функции в этой точке:
, если предел функции в данной точке равен значению функции в этой точке: ![]() .
.
Определение детализируется в следующих условиях:
1) Функция должна быть определена в точке ![]() , то есть должно существовать значение
, то есть должно существовать значение ![]() .
.
2) Должен существовать общий предел функции ![]() . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов:
. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: ![]() .
.
3) Предел функции в данной точке должен быть равен значению функции в этой точке: ![]() .
.
!!! Рекомендую законспектировать пункты, поскольку они потребуются для решения практических задач. Далее по тексту они будут отмечаться как Условие № 1, Условие № 2 и Условие № 3.
Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке ![]() .
.
Непрерывность функции на интервале формулируется остроумно и очень просто: функция непрерывна на интервале ![]() , если она непрерывна в каждой точке данного интервала.
, если она непрерывна в каждой точке данного интервала.
В частности, многие функции непрерывны на бесконечном интервале ![]() , то есть на множестве действительных чисел
, то есть на множестве действительных чисел ![]() . Это линейная функция, многочлены, экспонента, синус, косинус и др. И вообще, любая элементарная функция непрерывна на своей области определения, так, например, логарифмическая функция
. Это линейная функция, многочлены, экспонента, синус, косинус и др. И вообще, любая элементарная функция непрерывна на своей области определения, так, например, логарифмическая функция ![]() непрерывна на интервале
непрерывна на интервале ![]() . Надеюсь, к данному моменту вы достаточно хорошо представляете, как выглядят графики основных функций. Более подробную информацию об их непрерывности можно почерпнуть у доброго человека по фамилии Фихтенгольц.
. Надеюсь, к данному моменту вы достаточно хорошо представляете, как выглядят графики основных функций. Более подробную информацию об их непрерывности можно почерпнуть у доброго человека по фамилии Фихтенгольц.
С непрерывностью функции на отрезке ![]() и полуинтервалах
и полуинтервалах ![]() тоже всё несложно, но об этом уместнее рассказать на уроке о нахождении минимального и максимального значений функции на отрезке, а пока голову забивать не будем.
тоже всё несложно, но об этом уместнее рассказать на уроке о нахождении минимального и максимального значений функции на отрезке, а пока голову забивать не будем.
Классификация точек разрыва
Увлекательная жизнь функций богата всякими особенными точками, и точки разрыва лишь одна из страничек их биографии.
Примечание: на всякий случай остановлюсь на элементарном моменте: точка разрыва – это всегда отдельно взятая точка – не бывает «несколько точек разрыва подряд», то есть, нет такого понятия, как «интервал разрывов».
Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода. У каждого типа разрыва есть свои характерные особенности, которые мы рассмотрим прямо сейчас:
Точка разрыва первого рода
Если в точке ![]() нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода.
нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода.
Начнём с самого оптимистичного случая. По первоначальной задумке урока я хотел рассказать теорию «в общем виде», но чтобы продемонстрировать реальность материала, остановился на варианте с конкретными действующими лицами.
Уныло, как фото молодожёнов на фоне Вечного огня, но нижеследующий кадр общепринят. Изобразим на чертеже график функции ![]() :
:

Данная функция непрерывна на всей числовой прямой, кроме точки ![]() . И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
. И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
![]() (Условие № 2 непрерывности выполнено).
(Условие № 2 непрерывности выполнено).
Но функция не определена в точке ![]() , следовательно, нарушено Условие № 1 непрерывности, и функция
, следовательно, нарушено Условие № 1 непрерывности, и функция ![]() терпит разрыв в данной точке.
терпит разрыв в данной точке.
Разрыв такого вида (с существующим общим пределом) называют устранимым разрывом. Почему устранимым? Потому что функцию можно доопределить в точке разрыва:
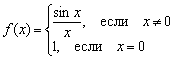
Странно выглядит? Возможно. Но такая запись функции ничему не противоречит! Теперь разрыв устранён и все счастливы:
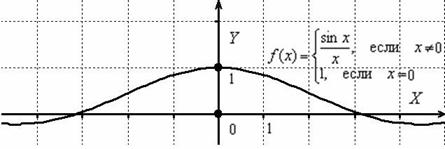
Выполним формальную проверку:
1) ![]() – функция определена в данной точке;
– функция определена в данной точке;
2) ![]() – общий предел существует;
– общий предел существует;
3) ![]() – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, все три условия выполнены, и функция непрерывна в точке ![]() по определению непрерывности функции в точке.
по определению непрерывности функции в точке.
Впрочем, ненавистники матана могут доопределить функцию нехорошим способом, например  :
:
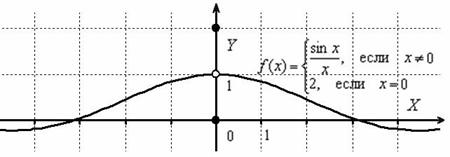
Любопытно, что здесь выполнены первые два условия непрерывности:
1) ![]() – функция определена в данной точке;
– функция определена в данной точке;
2) ![]() – общий предел существует.
– общий предел существует.
Но третий рубеж не пройден: ![]() , то есть предел функции в точке не равен значению данной функции в данной точке.
, то есть предел функции в точке не равен значению данной функции в данной точке.
Таким образом, в точке ![]() функция терпит разрыв.
функция терпит разрыв.
Второй, более грустный случай носит название разрыва первого рода со скачком. А грусть навевают односторонние пределы, которые конечны и различны. Пример изображён на втором чертеже урока. Такой разрыв возникает, как правило, в кусочно-заданных функциях, о которых уже упоминалось в статье о преобразованиях графиков.
Рассмотрим кусочную функцию  и выполним её чертёж. Как построить график? Очень просто. На полуинтервале
и выполним её чертёж. Как построить график? Очень просто. На полуинтервале ![]() чертим фрагмент параболы
чертим фрагмент параболы ![]() (зеленый цвет), на интервале
(зеленый цвет), на интервале ![]() – отрезок прямой
– отрезок прямой ![]() (красный цвет) и на полуинтервале
(красный цвет) и на полуинтервале ![]() – прямую
– прямую ![]() (синий цвет).
(синий цвет).
При этом в силу неравенства ![]() значение
значение ![]() определено для квадратичной функции
определено для квадратичной функции ![]() (зелёная точка), и в силу неравенства
(зелёная точка), и в силу неравенства ![]() , значение
, значение ![]() определено для линейной функции
определено для линейной функции ![]() (синяя точка):
(синяя точка):
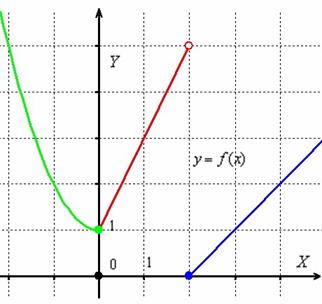
В самом-самом тяжёлом случае следует прибегнуть к поточечному построению каждого куска графика (см. первый урок о графиках функций).
Сейчас нас будет интересовать только точка ![]() . Исследуем её на непрерывность:
. Исследуем её на непрерывность:
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Вычислим односторонние пределы.
Слева у нас красный отрезок прямой, поэтому левосторонний предел: ![]()
Справа – синяя прямая, и правосторонний предел: ![]()
В результате получены конечные числа, причем они не равны. Поскольку односторонние пределы конечны и различны: ![]() , то наша функция терпит разрыв первого рода со скачком.
, то наша функция терпит разрыв первого рода со скачком.
Логично, что разрыв не устраним – функцию действительно не доопределить и «не склеить», как в предыдущем примере.
Точки разрыва второго рода
Обычно к данной категории хитро относят все остальные случаи разрыва. Всё перечислять не буду, поскольку на практике в 99%-ти процентах задач вам встретится бесконечный разрыв – когда левосторонний или правосторонний, а чаще, оба предела бесконечны.
И, конечно же, самая напрашивающаяся картинка – гипербола в точке ноль. Здесь оба односторонних предела бесконечны: ![]() , следовательно, функция
, следовательно, функция ![]() терпит разрыв второго рода в точке
терпит разрыв второго рода в точке ![]() .
.
Я стараюсь наполнять свои статьи максимально разнообразным содержанием, поэтому давайте посмотрим на график функции ![]() , который ещё не встречался:
, который ещё не встречался:
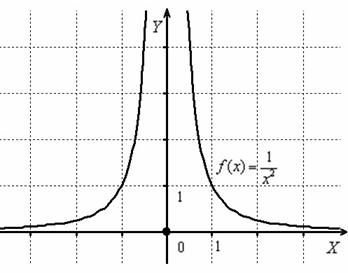
Исследуем на непрерывность точку ![]() по стандартной схеме:
по стандартной схеме:
1) Функция не определена в данной точке, поскольку знаменатель обращается в ноль.
Конечно, можно сразу сделать вывод о том, что функция терпит разрыв в точке ![]() , но хорошо бы классифицировать характер разрыва, что часто требуется по условию. Для этого:
, но хорошо бы классифицировать характер разрыва, что часто требуется по условию. Для этого:
2) Вычислим односторонние пределы:

Напоминаю, что под записью ![]() понимается бесконечно малое отрицательное число, а под записью
понимается бесконечно малое отрицательное число, а под записью ![]() – бесконечно малое положительное число.
– бесконечно малое положительное число.
Односторонние пределы бесконечны, значит, функция ![]() терпит разрыв 2-го рода в точке
терпит разрыв 2-го рода в точке ![]() . Ось ординат является вертикальной асимптотой для графика.
. Ось ординат является вертикальной асимптотой для графика.
Не редка ситуация, когда оба односторонних предела существуют, но бесконечен только один из них, например:
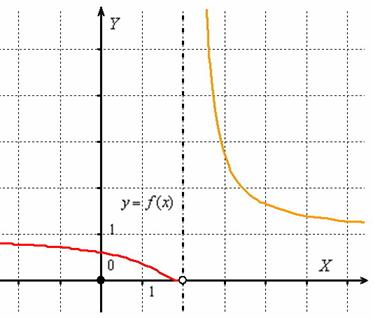
Это график функции ![]() .
.
Исследуем на непрерывность точку ![]() :
:
1) Функция не определена в данной точке.
2) Вычислим односторонние пределы:

О методике вычисления таких односторонних пределов поговорим в двух последних примерах лекции, хотя многие читатели всё уже увидели и догадались.
Левосторонний предел конечен и равен нулю (в саму точку мы «не заходим»), но правосторонний предел бесконечен и оранжевая ветка графика бесконечно близко приближается к своей вертикальной асимптоте, заданной уравнением ![]() (чёрный пунктир).
(чёрный пунктир).
Таким образом, функция ![]() терпит разрыв второго рода в точке
терпит разрыв второго рода в точке ![]() .
.
Как и для разрыва 1-го рода, в самой точке разрыва функция может быть определена. Например, для кусочной функции  смело ставим чёрную жирную точку в начале координат. Справа же – ветка гиперболы, и правосторонний предел бесконечен. Думаю, почти все представили, как выглядит этот график.
смело ставим чёрную жирную точку в начале координат. Справа же – ветка гиперболы, и правосторонний предел бесконечен. Думаю, почти все представили, как выглядит этот график.
То, чего все с нетерпением ждали:
Как исследовать функцию на непрерывность?
Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:
Пример 1
Исследовать функцию ![]() на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение:
1) Под прицел попадает единственная точка ![]() , в которой функция не определена.
, в которой функция не определена.
2) Вычислим односторонние пределы:

Односторонние пределы конечны и равны.
Таким образом, в точке ![]() функция терпит устранимый разрыв.
функция терпит устранимый разрыв.
Как выглядит график данной функции?
Хочется провести упрощение ![]() , и вроде бы получается обычная парабола. НО исходная функция не определена в точке
, и вроде бы получается обычная парабола. НО исходная функция не определена в точке ![]() , поэтому обязательна следующая оговорка:
, поэтому обязательна следующая оговорка:
![]()
Выполним чертёж:
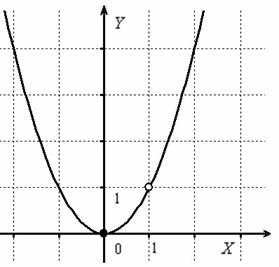
Ответ: функция непрерывна на всей числовой прямой кроме точки ![]() , в которой она терпит устранимый разрыв.
, в которой она терпит устранимый разрыв.
Функцию можно доопределить хорошим или не очень способом, но по условию этого не требуется.
Вы скажете, пример надуманный? Ничуть. Десятки раз встречалось на практике. Почти все задачи сайта родом из реальных самостоятельных и контрольных работ.
Разделаемся с любимыми модулями:
Пример 2
Исследовать функцию ![]() на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение: почему-то студенты боятся и не любят функции с модулем, хотя ничего сложного в них нет. Таких вещей мы уже немного коснулись на уроке Геометрические преобразования графиков. Поскольку модуль неотрицателен, то он раскрывается следующим образом: ![]() , где «альфа» – некоторое выражение. В данном случае
, где «альфа» – некоторое выражение. В данном случае ![]() , и наша функция должна расписаться кусочным образом:
, и наша функция должна расписаться кусочным образом:
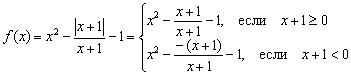
Но дроби обоих кусков предстоит сократить на ![]() . Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке
. Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке ![]() , так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие
, так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие ![]() , и первое неравенство
, и первое неравенство ![]() сделать строгим:
сделать строгим:

Теперь об ОЧЕНЬ ПОЛЕЗНОМ приёме решения: перед чистовым оформлением задачи на черновике выгодно сделать чертёж (независимо от того, требуется он по условию или нет). Это поможет, во-первых, сразу увидеть точки непрерывности и точки разрыва, а, во-вторых, 100%-но убережёт от ошибок при нахождении односторонних пределов.
Выполним чертёж. В соответствии с нашими выкладками, слева от точки ![]() необходимо начертить фрагмент параболы
необходимо начертить фрагмент параболы ![]() (синий цвет), а справа – кусок параболы
(синий цвет), а справа – кусок параболы ![]() (красный цвет), при этом функция не определена в самой точке
(красный цвет), при этом функция не определена в самой точке ![]() :
:
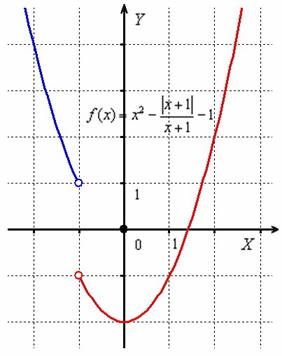
Если есть сомнения, возьмите несколько значений «икс», подставьте их в функцию ![]() (не забывая, что модуль уничтожает возможный знак «минус») и сверьтесь с графиком.
(не забывая, что модуль уничтожает возможный знак «минус») и сверьтесь с графиком.
Исследуем функцию на непрерывность аналитически:
1) Функция не определена в точке ![]() , поэтому сразу можно сказать, что не является в ней непрерывной.
, поэтому сразу можно сказать, что не является в ней непрерывной.
2) Установим характер разрыва, для этого вычислим односторонние пределы:

Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке ![]() . Ещё раз заметьте, что при нахождении пределов не имеет значения, определена функция в точке разрыва или нет.
. Ещё раз заметьте, что при нахождении пределов не имеет значения, определена функция в точке разрыва или нет.
Теперь остаётся перенести чертёж с черновика (он сделан как бы с помощью исследования ;-)) и завершить задание:
Ответ: функция непрерывна на всей числовой прямой кроме точки ![]() , в которой она терпит разрыв первого рода со скачком.
, в которой она терпит разрыв первого рода со скачком.
Иногда требуют дополнительно указать скачок разрыва. Вычисляется он элементарно – из правого предела нужно вычесть левый предел: ![]() , то есть в точке разрыва наша функция прыгнула на 2 единицы вниз (о чём нам сообщает знак «минус»).
, то есть в точке разрыва наша функция прыгнула на 2 единицы вниз (о чём нам сообщает знак «минус»).
Пример 3
Исследовать функцию ![]() на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.
Это пример для самостоятельного решения, примерный образец решения в конце урока.
Перейдём к наиболее популярной и распространённой версии задания, когда функция состоит из трёх кусков:
Пример 4
Исследовать функцию на непрерывность и построить график функции  .
.
Решение: очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике, технику построения я достаточно подробно закомментировал в первой части статьи. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства ![]() значение
значение ![]() принадлежит прямой
принадлежит прямой ![]() (зелёная точка), и в силу неравенство
(зелёная точка), и в силу неравенство ![]() значение
значение ![]() принадлежит параболе
принадлежит параболе ![]() (красная точка):
(красная точка):
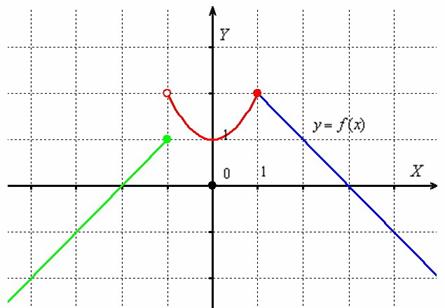
Ну вот, в принципе, всё понятно =) Осталось оформить решение. Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:
I) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:

Односторонние пределы конечны и различны, значит, функция ![]() терпит разрыв 1-го рода со скачком в точке
терпит разрыв 1-го рода со скачком в точке ![]() .
.
Вычислим скачок разрыва как разность правого и левого пределов:
![]() , то есть, график рванул на одну единицу вверх.
, то есть, график рванул на одну единицу вверх.
II) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:

![]() – односторонние пределы конечны и равны, значит, существует общий предел.
– односторонние пределы конечны и равны, значит, существует общий предел.
3) ![]() – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция ![]() непрерывна в точке
непрерывна в точке ![]() по определению непрерывности функции в точке.
по определению непрерывности функции в точке.
На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:
Ответ: функция непрерывна на всей числовой прямой, кроме точки ![]() , в которой она терпит разрыв первого рода со скачком.
, в которой она терпит разрыв первого рода со скачком.
Готово.
Пример 5
Исследовать функцию на непрерывность и построить её график  .
.
Это пример для самостоятельного решения, краткое решение и примерный образец оформления задачи в конце урока.
Может сложиться впечатление, что в одной точке функция обязательно должна быть непрерывной, а в другой – обязательно должен быть разрыв. На практике это далеко не всегда так. Постарайтесь не пренебрегать оставшимися примерами – будет несколько интересных и важных фишек:
Пример 6
Дана функция  . Исследовать функцию на непрерывность в точках
. Исследовать функцию на непрерывность в точках ![]() . Построить график.
. Построить график.
Решение: и снова сразу выполним чертёж на черновике:
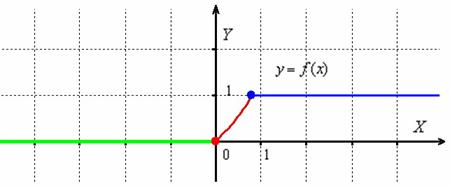
Особенность данного графика состоит в том, что при ![]() кусочная функция задаётся уравнением оси абсцисс
кусочная функция задаётся уравнением оси абсцисс ![]() . Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение
. Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение ![]() относится к ветке тангенса (красная точка), а значение
относится к ветке тангенса (красная точка), а значение ![]() принадлежит прямой
принадлежит прямой ![]() .
.
Из чертежа всё понятно – функция непрерывна на всей числовой прямой, осталось оформить решение, которое доводится до полного автоматизма буквально после 3-4 подобных примеров:
I) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Вычислим односторонние пределы:

![]() , значит, общий предел существует.
, значит, общий предел существует.
На всякий пожарный напомню тривиальный факт: предел константы равен самой константе. В данном случае предел нуля равен самому нулю (левосторонний предел).
Едем дальше:
3) ![]() – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция ![]() непрерывна в точке
непрерывна в точке ![]() по определению непрерывности функции в точке.
по определению непрерывности функции в точке.
II) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:
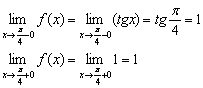
И здесь – предел единицы равен самой единице.
![]() – общий предел существует.
– общий предел существует.
3) 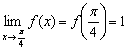 – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция ![]() непрерывна в точке
непрерывна в точке ![]() по определению непрерывности функции в точке.
по определению непрерывности функции в точке.
Как обычно, после исследования переносим наш чертёж на чистовик.
Ответ: функция непрерывна в точках ![]() .
.
Обратите внимание, что в условии нас ничего не спрашивали про исследование всей функции на непрерывность, и хорошим математическим тоном считается формулировать точный и чёткий ответ на поставленный вопрос. Кстати, если по условию не требуется строить график, то вы имеете полное право его и не строить (правда, потом преподаватель может заставить это сделать).
Небольшая математическая «скороговорка» для самостоятельного решения:
Пример 7
Дана функция 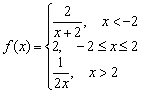 . Исследовать функцию на непрерывность в точках
. Исследовать функцию на непрерывность в точках ![]() . Классифицировать точки разрыва, если они есть. Выполнить чертёж.
. Классифицировать точки разрыва, если они есть. Выполнить чертёж.
Постарайтесь правильно «выговорить» все «слова» =) И график нарисовать поточнее, точность, она везде лишней не будет ;-)
Как вы помните, я рекомендовал незамедлительно выполнять чертёж на черновике, но время от времени попадаются такие примеры, где не сразу сообразишь, как выглядит график. Поэтому в ряде случаев выгодно сначала найти односторонние пределы и только потом на основе исследования изобразить ветви. В двух заключительных примерах мы, кроме того, освоим технику вычисления некоторых односторонних пределов:
Пример 8
Исследовать на непрерывность функцию 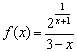 и построить её схематический график.
и построить её схематический график.
Решение: нехорошие точки очевидны: ![]() (обращает в ноль знаменатель показателя) и
(обращает в ноль знаменатель показателя) и ![]() (обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование:
(обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование:
I) Исследуем на непрерывность точку ![]()
1) Функция не определена в данной точке.
2) Найдём односторонние пределы:
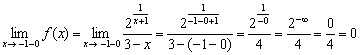
Обратите внимание на типовой приём вычисления одностороннего предела: в функцию вместо «икса» мы подставляем ![]() . В знаменателе никакого криминала: «добавка» «минус ноль» не играет роли, и получается «четыре». А вот в числителе происходит небольшой триллер: сначала в знаменателе показателя
. В знаменателе никакого криминала: «добавка» «минус ноль» не играет роли, и получается «четыре». А вот в числителе происходит небольшой триллер: сначала в знаменателе показателя ![]() убиваем –1 и 1, в результате чего получается
убиваем –1 и 1, в результате чего получается ![]() . Единица, делённая на бесконечно малое отрицательное число, равна «минус бесконечности», следовательно:
. Единица, делённая на бесконечно малое отрицательное число, равна «минус бесконечности», следовательно: ![]() . И, наконец, «двойка» в бесконечно большой отрицательной степени равна нулю:
. И, наконец, «двойка» в бесконечно большой отрицательной степени равна нулю: ![]() . Или, если ещё подробнее:
. Или, если ещё подробнее: ![]() .
.
Вычислим правосторонний предел:

И здесь – вместо «икса» подставляем ![]() . В знаменателе «добавка»
. В знаменателе «добавка» ![]() снова не играет роли:
снова не играет роли: ![]() . В числителе проводятся аналогичные предыдущему пределу действия: уничтожаем противоположные числа и делим единицу на бесконечно малое положительное число:
. В числителе проводятся аналогичные предыдущему пределу действия: уничтожаем противоположные числа и делим единицу на бесконечно малое положительное число: ![]()
Правосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке ![]() .
.
II) Исследуем на непрерывность точку ![]()
1) Функция не определена в данной точке.
2) Вычислим левосторонний предел:

Метод такой же: подставляем в функцию вместо «икса» ![]() . В числителе ничего интересного – получается конечное положительно число
. В числителе ничего интересного – получается конечное положительно число ![]() . А в знаменателе раскрываем скобки, убираем «тройки», и решающую роль играет «добавка»
. А в знаменателе раскрываем скобки, убираем «тройки», и решающую роль играет «добавка» ![]() .
.
По итогу, конечное положительное число, делённое на бесконечно малое положительное число, даёт «плюс бесконечность»: ![]() .
.
Правосторонний предел, как брат близнец, за тем лишь исключением, что в знаменателе выплывает бесконечно малое отрицательное число:

Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке ![]() .
.
Таким образом, у нас две точки разрыва, и, очевидно, три ветки графика. Для каждой ветки целесообразно провести поточечное построение, т.е. взять несколько значений «икс» и подставить их в ![]() . Заметьте, что по условию допускается построение схематического чертежа, и такое послабление естественно для ручной работы. Я строю графики с помощью проги, поэтому не имею подобных затруднений, вот достаточно точная картинка:
. Заметьте, что по условию допускается построение схематического чертежа, и такое послабление естественно для ручной работы. Я строю графики с помощью проги, поэтому не имею подобных затруднений, вот достаточно точная картинка:
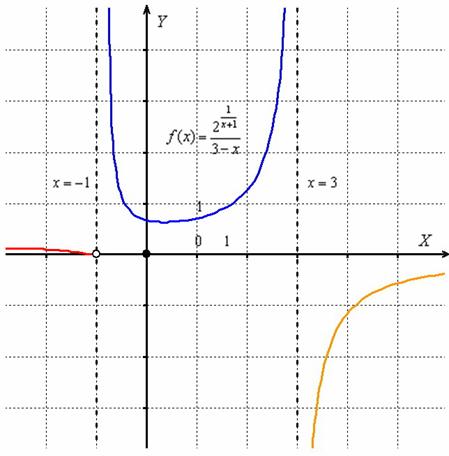
Прямые ![]() являются вертикальными асимптотами для графика данной функции.
являются вертикальными асимптотами для графика данной функции.
Ответ: функция непрерывна на всей числовой прямой кроме точек ![]() , в которых она терпит разрывы 2-го рода.
, в которых она терпит разрывы 2-го рода.
Более простая функция для самостоятельного решения:
Пример 9
Исследовать на непрерывность функцию ![]() и выполнить схематический чертёж.
и выполнить схематический чертёж.
Примерный образец решения в конце, который подкрался незаметно. Однако по просьбам учащихся ещё один случай:
Пример 10
Исследовать на непрерывность функцию ![]() в точке
в точке ![]() .
.
Решение, как обычно, по пунктам, новизна будет в пределах:
1) Очевидно, функция не определена в данной точке, ибо знаменатель обращается в ноль:
![]()
2) Вычислим односторонние пределы в точке ![]() :
:
![]()
Справка: если основание степени ![]() , то
, то ![]() , а
, а ![]() . И сразу на другой случай жизни: если основание степени
. И сразу на другой случай жизни: если основание степени ![]() , то наоборот:
, то наоборот: ![]()
Второй односторонний предел:
![]()
Односторонние пределы бесконечны и различны по знаку, таким образом, функция терпит разрыв 2-го рода в точке ![]() .
.
По условию, чертёж не требовался, но мне не сложно, сейчас только раскопаю шаблоны семилетней давности :) …ого, секунд 20 потребовалось всего и ещё минуты три на чертёж:

Вот такое вот нечто…, никогда не думал, что свои шутки буду пробивать по Поиску, хотел пошутить, да оказалось повтором :) И коль скоро шутки нет, то факультативное задание для тренировки: найдите пределы этой же функции на «минус» и «плюс» бесконечности.
Ответ: функция терпит бесконечный разрыв в точке ![]()
Спасибо за ваши письма! – они помогают сделать материал более полным и качественным.
До скорых встреч!
Решения и ответы:
Пример 3: Решение: преобразуем функцию: ![]() . Учитывая правило раскрытия модуля
. Учитывая правило раскрытия модуля ![]() и тот факт, что
и тот факт, что ![]() , перепишем функцию в кусочном виде:
, перепишем функцию в кусочном виде:
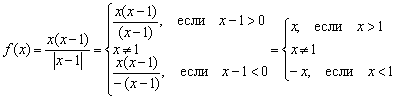
Исследуем функцию на непрерывность.
1) Функция не определена в точке ![]() .
.
2) Вычислим односторонние пределы:
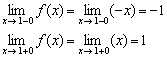
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке ![]() . Выполним чертёж:
. Выполним чертёж:
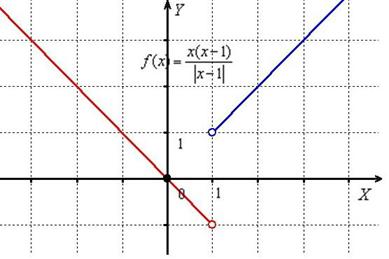
Ответ: функция непрерывна на всей числовой прямой кроме точки ![]() , в которой она терпит разрыв первого рода со скачком. Скачок разрыва:
, в которой она терпит разрыв первого рода со скачком. Скачок разрыва: ![]() (две единицы вверх).
(две единицы вверх).
Пример 5: Решение: каждая из трёх частей функции непрерывна на своём интервале.
I) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Вычислим односторонние пределы:

![]() , значит, общий предел существует.
, значит, общий предел существует.
3) ![]() – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция ![]() непрерывна в точке
непрерывна в точке ![]() по определению непрерывности функции в точке.
по определению непрерывности функции в точке.
II) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:

Односторонние пределы конечны и различны, значит, функция ![]() терпит разрыв 1-го рода со скачком в точке
терпит разрыв 1-го рода со скачком в точке ![]() .
.
Скачок разрыва: ![]() (пять единиц вниз).
(пять единиц вниз).
Чертёж можно найти в первой части статьи.
Ответ: функция непрерывна на всей числовой прямой, кроме точки ![]() , в которой она терпит разрыв первого рода со скачком.
, в которой она терпит разрыв первого рода со скачком.
Пример 7: Решение:
I) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:

Левосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке ![]() .
.
II) Исследуем на непрерывность точку ![]()
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:

Односторонние пределы конечны и различны, значит, функция ![]() терпит разрыв 1-го рода со скачком в точке
терпит разрыв 1-го рода со скачком в точке ![]() .
.
Выполним чертёж:
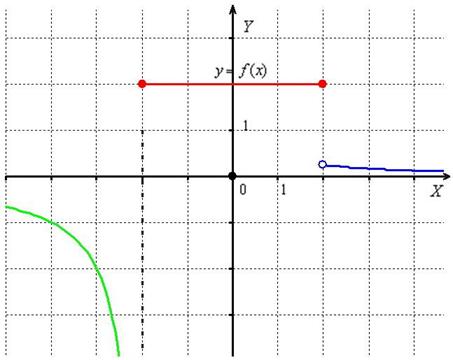
Ответ: В точке ![]() функция терпит разрыв 2-го рода, в точке
функция терпит разрыв 2-го рода, в точке ![]() функция терпит разрыв 1-го рода со скачком.
функция терпит разрыв 1-го рода со скачком.
Пример 9: Решение: исследуем на непрерывность точку ![]() :
:
1) Функция не определена в данной точке.
2) Вычислим односторонние пределы:

Левосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке ![]() .
.
Выполним чертёж:
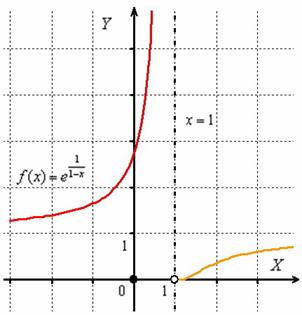
Ответ: функция непрерывна на всей числовой прямой кроме точки ![]() , в которой она терпит разрыв 2-го рода.
, в которой она терпит разрыв 2-го рода.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright