


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить площадь фигуры и объём тела вращения,
если линия задана параметрически?
На занятиях Вычисление площади с помощью определённого интеграла и Объем тела вращения мы рассмотрели два самых важных приложения определённого интеграла, в которых демонстрационная криволинейная трапеция ограничена осью абсцисс, отрезками прямых ![]() и графиком функции
и графиком функции ![]() , которая непрерывна и не меняет знак на отрезке «а-бэ». Но в некоторых практических заданиях функция может быть задана в параметрическом виде
, которая непрерывна и не меняет знак на отрезке «а-бэ». Но в некоторых практических заданиях функция может быть задана в параметрическом виде ![]() , и наша сегодняшняя задача – научиться считать площадь и объем, если вышла такая незадача =) Понятие параметрической формы я достаточно подробно раскрыл в статье о производной параметрически заданной функции, и в курсе аналитической геометрии на уроках об уравнении прямой на плоскости и уравнениях прямой в пространстве.
, и наша сегодняшняя задача – научиться считать площадь и объем, если вышла такая незадача =) Понятие параметрической формы я достаточно подробно раскрыл в статье о производной параметрически заданной функции, и в курсе аналитической геометрии на уроках об уравнении прямой на плоскости и уравнениях прямой в пространстве.
Встречайте старую знакомую:
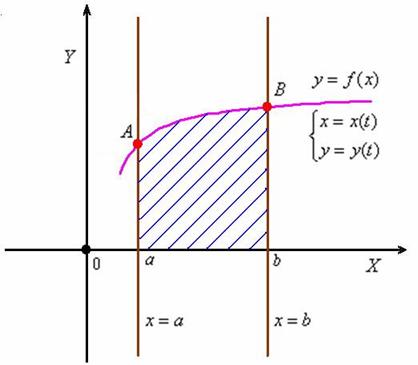
Криволинейную трапецию гордо венчает график ![]() , и, как вы знаете, её площадь рассчитывается с помощью определённого интеграла по элементарной формуле
, и, как вы знаете, её площадь рассчитывается с помощью определённого интеграла по элементарной формуле  или, если короче:
или, если короче:  .
.
Рассмотрим ситуацию, когда эта же функция задана в параметрическом виде ![]() .
.
Как найти площадь в этом случае?
При некотором вполне конкретном значении параметра ![]() параметрические уравнения будут определять координаты точки
параметрические уравнения будут определять координаты точки ![]() , а при другом вполне конкретном значении
, а при другом вполне конкретном значении ![]() – координаты точки
– координаты точки ![]() . Когда «тэ» изменяется от
. Когда «тэ» изменяется от ![]() до
до ![]() включительно, параметрические уравнения как раз и «прорисовывают» кривую
включительно, параметрические уравнения как раз и «прорисовывают» кривую ![]() . Думаю, на счёт пределов интегрирования стало всё понятно. Теперь в интеграл
. Думаю, на счёт пределов интегрирования стало всё понятно. Теперь в интеграл  вместо «икса» и «игрека» подставляем функции
вместо «икса» и «игрека» подставляем функции ![]() и раскрываем дифференциал:
и раскрываем дифференциал:

Примечание: подразумевается, что функции ![]() непрерывны на промежутке интегрирования и, кроме того, функция
непрерывны на промежутке интегрирования и, кроме того, функция ![]() монотонна на нём.
монотонна на нём.
Формула объёма тела вращения получается так же просто:
Объём тела, получаемого вращением криволинейной трапеции вокруг оси ![]() , рассчитывается по формуле
, рассчитывается по формуле  или:
или:  . Подставляем в неё параметрические функции
. Подставляем в неё параметрические функции ![]() , а также пределы интегрирования
, а также пределы интегрирования ![]() :
:

Пожалуйста, занесите обе рабочие формулы в свой справочник.
По моим наблюдениям, задачи на нахождение объёма встречаются довольно редко, и поэтому значительная часть примеров данного урока будет посвящена нахождению площади. Не откладываем дело в долгий ящик:
Пример 1
Вычислить площадь криволинейной трапеции ![]() , если
, если ![]()
Решение: используем формулу  .
.
Сначала найдём производную. Дифференцирование осуществляется, само собой, по переменной «тэ», для краткости записи я не буду рисовать подстрочный индекс:
![]() .
.
Таким образом:

Ответ: ![]()
И сразу проанализируем важный вопрос:
Нужно ли в рассматриваемом типе задач выполнять чертёж?
Отвечу так: если повезёт с заданием, то можно и не выполнять. Как, например, в только что решенном примере, где само условие «заточено» под формулу, и чертёж с фигурой, площадь которой необходимо рассчитать, по существу, и не нужен.
Однако даже в очень простых случаях нас могут поджидать неожиданные сюрпризы. Так… сейчас придумаю что-нибудь… вот: вычислить площадь криволинейной трапеции ![]() , давайте с теми же пределами изменения параметра «тэ» от 1 до 4.
, давайте с теми же пределами изменения параметра «тэ» от 1 до 4.
Найдём производную: ![]()
Площадь: 
Но площадь не может быть отрицательной! Где ошибка?
В подобной ситуации, прежде всего, нужно проверить само решение. Выполняем тщательную проверку и убеждаемся, что с техникой всё в порядке. А может быть фигура расположена под осью ![]() , и поэтому изначально следовало поставить знак «минус» перед интегралом? Анализируем функцию
, и поэтому изначально следовало поставить знак «минус» перед интегралом? Анализируем функцию ![]() , «отвечающую за игреки». Нет – она вообще неотрицательна при любом допустимом значении параметра, а значит, фигура расположена выше оси абсцисс. Так почему же площадь получилась со знаком «минус»?!
, «отвечающую за игреки». Нет – она вообще неотрицательна при любом допустимом значении параметра, а значит, фигура расположена выше оси абсцисс. Так почему же площадь получилась со знаком «минус»?!
Разгадка в следующем: параметр «тэ» изменяется в пределах ![]() , но при его увеличении функция
, но при его увеличении функция ![]() убывает. Что это значит геометрически? Это значит, что мы двигаемся по оси
убывает. Что это значит геометрически? Это значит, что мы двигаемся по оси ![]() влево, и соответственно, параметрические уравнения
влево, и соответственно, параметрические уравнения ![]() «прочерчивают» линию справа налево. Но площадь криволинейной трапеции традиционно рассчитывается слева направо! Отсюда и «минус».
«прочерчивают» линию справа налево. Но площадь криволинейной трапеции традиционно рассчитывается слева направо! Отсюда и «минус».
В этой связи корректное решение оформляется примерно так: «нижнему пределу интегрирования соответствует значение ![]() , а верхнему пределу интегрирования – значение
, а верхнему пределу интегрирования – значение ![]() , таким образом:
, таким образом:  ». Здесь мы «заставили убывать сам параметр», чтобы интегрирование проходило в «правильном» направлении.
». Здесь мы «заставили убывать сам параметр», чтобы интегрирование проходило в «правильном» направлении.
Но на практике распространён и другой вариант: перед исходным интегралом изначально ставится «минус»:  с предварительным комментарием, что функция
с предварительным комментарием, что функция ![]() убывает на промежутке
убывает на промежутке ![]() (а то и без всяких пояснений ;-)).
(а то и без всяких пояснений ;-)).
Как видите, даже в таком простом примере волей-неволей пришлось прибегнуть к анализу (пусть и устному) геометрической информации, а во многих случаях без чертежа и вовсе обойтись очень трудно. Но беда в том, что изобразить график функции, заданной параметрически, не так-то просто и не так-то быстро, поэтому я рекомендую пользоваться программными средствами, например, моим графопостроителем.
Классическая задача по теме, которая разбирается всегда и везде:
Пример 2
Вычислить площадь эллипса ![]()
Решение: для определённости полагаем, что параметрические уравнения ![]() задают канонический эллипс с центром в начале координат, большой полуосью «а» и малой полуосью «бэ». То есть, по условию нам предложено не что иное, как
задают канонический эллипс с центром в начале координат, большой полуосью «а» и малой полуосью «бэ». То есть, по условию нам предложено не что иное, как
найти площадь эллипса 
Очевидно, что параметрические функции периодичны, и ![]() . Казалось бы, можно заряжать формулу, однако не всё так прозрачно. Выясним направление, в котором параметрические уравнения «вычерчивают» эллипс. В качестве ориентира найдём несколько точек, которые соответствуют наиболее простым значениям параметра:
. Казалось бы, можно заряжать формулу, однако не всё так прозрачно. Выясним направление, в котором параметрические уравнения «вычерчивают» эллипс. В качестве ориентира найдём несколько точек, которые соответствуют наиболее простым значениям параметра:

Легко уловить, что при изменении параметра «тэ» от нуля до «двух пи» параметрические уравнения «вычерчивают» эллипс против часовой стрелки:
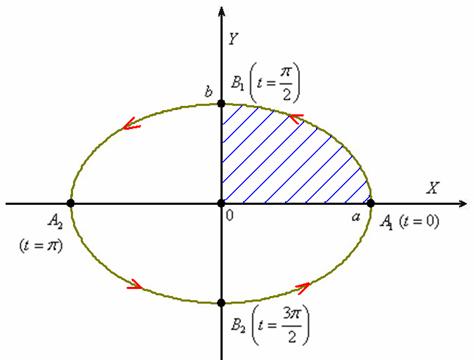
В силу симметричности фигуры, вычислим часть площади в 1-й координатной четверти, а результат умножим на 4. Здесь мы наблюдаем принципиально такую же картину, которую я комментировал чуть выше: параметрические уравнения «прорисовывают» дугу эллипса «в противоход» оси ![]() , но площадь фигуры считается слева направо! Поэтому нижнему пределу интегрирования соответствует значение
, но площадь фигуры считается слева направо! Поэтому нижнему пределу интегрирования соответствует значение ![]() , а верхнему пределу – значение
, а верхнему пределу – значение ![]() .
.
Как я уже советовал на уроке Площадь в полярных координатах, учетверить результат лучше сразу же:

Интеграл ![]() (если у кого-то вдруг обнаружился такой невероятный пробел) разобран на уроке Интегралы от тригонометрических функций.
(если у кого-то вдруг обнаружился такой невероятный пробел) разобран на уроке Интегралы от тригонометрических функций.
Ответ: ![]()
По сути, мы вывели формулу для нахождения площади эллипса. И если на практике вам встретится задача с конкретными значениями «а» и «бэ», то вы легко сможете выполнить сверку/проверку, поскольку задача решена в общем виде.
Площадь эллипса рассчитывается и в прямоугольных координатах, для этого из уравнения ![]() необходимо выразить «игрек» и решить задачу точь-в-точь по образцу Примера №4 статьи Эффективные методы решения определённых интегралов. Обязательно посмотрите на этот пример и сравните, насколько проще вычислить площадь эллипса, если он задан параметрически.
необходимо выразить «игрек» и решить задачу точь-в-точь по образцу Примера №4 статьи Эффективные методы решения определённых интегралов. Обязательно посмотрите на этот пример и сравните, насколько проще вычислить площадь эллипса, если он задан параметрически.
И, конечно же, чуть не забыл, параметрические уравнения ![]() могут задавать окружность либо эллипс в неканоническом положении.
могут задавать окружность либо эллипс в неканоническом положении.
Пример 3
Вычислить площадь одной арки циклоиды ![]()
Чтобы решить задачу, нужно знать, что такое циклоида или хотя бы чисто формально выполнить чертеж. Примерный образец оформления в конце урока. Впрочем, не буду вас отправлять за тридевять земель, на график этой линии можно посмотреть в следующей задаче:
Пример 4
Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями 
Решение: параметрические уравнения ![]() задают циклоиду, и ограничение
задают циклоиду, и ограничение ![]() указывает на тот факт, что речь идёт о её первой арке, которая «прорисовывается», когда значение параметра изменяется в пределах
указывает на тот факт, что речь идёт о её первой арке, которая «прорисовывается», когда значение параметра изменяется в пределах ![]() . Заметьте, что здесь «правильное» направление этой «прорисовки» (слева направо), а значит, не возникнет заморочек с пределами интегрирования. Но зато появится куча других прикольных вещей =) Уравнение
. Заметьте, что здесь «правильное» направление этой «прорисовки» (слева направо), а значит, не возникнет заморочек с пределами интегрирования. Но зато появится куча других прикольных вещей =) Уравнение ![]() задаёт прямую, параллельную оси абсцисс и дополнительное условие
задаёт прямую, параллельную оси абсцисс и дополнительное условие ![]() (см. линейные неравенства) сообщает нам о том, что нужно вычислить площадь следующей фигуры:
(см. линейные неравенства) сообщает нам о том, что нужно вычислить площадь следующей фигуры:
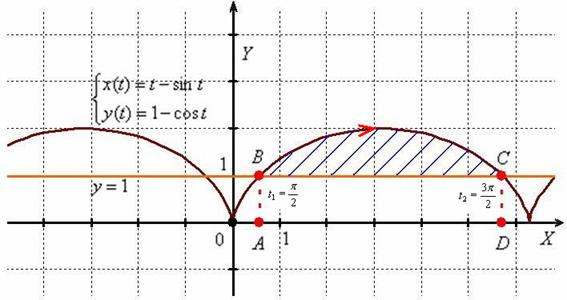
Искомую заштрихованную фигуру я буду ассоциативно называть «крышей дома», прямоугольник ![]() – «стеной дома», а всю конструкцию (стена + крыша) – «фасадом дома». Хотя это сооружение больше напоминает какой-то коровник =)
– «стеной дома», а всю конструкцию (стена + крыша) – «фасадом дома». Хотя это сооружение больше напоминает какой-то коровник =)
Чтобы найти площадь «крыши» необходимо из площади «фасада» вычесть площадь «стены».
Сначала займёмся «фасадом». Для нахождения его площади нужно выяснить значения ![]() , которые задают точки пересечения прямой
, которые задают точки пересечения прямой ![]() с первой аркой циклоиды (точки
с первой аркой циклоиды (точки ![]() и
и ![]() ). В параметрическое уравнение
). В параметрическое уравнение ![]() подставим
подставим ![]() :
:
![]()
Тригонометрическое уравнение ![]() легко решить, банально взглянув на график косинуса: на промежутке
легко решить, банально взглянув на график косинуса: на промежутке ![]() равенству
равенству ![]() удовлетворяют два корня:
удовлетворяют два корня: ![]() . В принципе, всё понятно, но, тем не менее, перестрахуемся и подставим их в уравнение
. В принципе, всё понятно, но, тем не менее, перестрахуемся и подставим их в уравнение ![]() :
:
![]() – это «иксовая» координата точки
– это «иксовая» координата точки ![]() ;
;
![]() – а это «иксовая» координата точки
– а это «иксовая» координата точки ![]() .
.
Таким образом, мы убедились в том, что значение параметра ![]() соответствует точке
соответствует точке ![]() , а значение
, а значение ![]() – точке
– точке ![]() .
.
Вычислим площадь «фасада». Для более компактной записи функция ![]() часто дифференцируется прямо под интегралом:
часто дифференцируется прямо под интегралом:

Площадь «стены» можно вычислить «школьным» методом, перемножив длины смежных сторон прямоугольника. Длина ![]() очевидна, осталось найти
очевидна, осталось найти ![]() . Она рассчитывается как разность «иксовых» координат точек «цэ» и «бэ» (найдены ранее):
. Она рассчитывается как разность «иксовых» координат точек «цэ» и «бэ» (найдены ранее):
![]()
Площадь «стены»: ![]()
Разумеется, её не стыдно найти и с помощью простейшего определённого интеграла от функции ![]() на отрезке
на отрезке ![]() :
:

В результате, площадь «крыши»:
![]()
Ответ: ![]()
И, конечно же, при наличии чертежа прикидываем по клеточкам, похож ли полученный результат на правду. Похож.
Следующая задача для самостоятельного решения:
Пример 5
Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями 
Кратко систематизируем алгоритм решения:
– В большинстве случаев придётся выполнить чертёж и определить фигуру, площадь которой требуется найти.
– На втором шаге следует понять, каким образом рассчитывается искомая площадь: это может быть одиночная криволинейная трапеция, может быть разность площадей, может быть сумма площадей – короче говоря, все те фишки, которые мы рассматривали на уроке Вычисление площади с помощью определённого интеграла.
– На третьем шаге надо проанализировать, целесообразно ли пользоваться симметрией фигуры (если она симметрична), после чего узнать пределы интегрирования (начальное и конечное значение параметра). Обычно для этого необходимо решить простейшее тригонометрическое уравнение – здесь можно использовать аналитический метод, графический метод или бесхитростный подбор нужных корней по тригонометрической таблице.
! Не забываем, что параметрические уравнения могут «прорисовывать» линию и справа налево, в этом случае делаем соответствующую оговорку и поправку в рабочей формуле.
– И на завершающем этапе проводятся технические вычисления. Правдоподобность полученного ответа всегда приятно оценить по чертежу.
А сейчас долгожданная встреча со звёздой:
Пример 6
Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями 
Решение: кривая, заданная уравнениями  является астроидой, и линейное неравенство
является астроидой, и линейное неравенство ![]() однозначно определяет заштрихованную на чертеже фигуру:
однозначно определяет заштрихованную на чертеже фигуру:

Найдём значения параметра, которые определяют точки пересечения прямой и астроиды. Для этого подставим ![]() в параметрическое уравнение
в параметрическое уравнение ![]() :
:

Способы решения подобного уравнения уже перечислены выше, в частности, эти корни легко подбираются по тригонометрической таблице.
Фигура симметрична относительно оси абсцисс, поэтому вычислим верхнюю половинку площади (синяя штриховка), а результат удвоим.
Подставим значение ![]() в параметрическое уравнение
в параметрическое уравнение ![]() :
: 
В результате получена «игрековая» координата верхней (нужной нам) точки пересечения астроиды и прямой.
Правой вершине астроиды, очевидно, соответствует значение ![]() . Выполним на всякий случай проверку:
. Выполним на всякий случай проверку:
 , что и требовалось проверить.
, что и требовалось проверить.
Как и в случае с эллипсом, параметрические уравнения «прорисовывают» дугу астроиды справа налево. Для разнообразия оформлю концовку вторым способом: при изменении параметра в пределах ![]() функция
функция ![]() убывает, следовательно (не забываем удвоить!!):
убывает, следовательно (не забываем удвоить!!):

Интеграл получился довольно громоздкий, и чтобы «не таскать всё за собой» тут лучше прервать решение и преобразовать подынтегральную функцию отдельно. Стандартно понижаем степень с помощью тригонометрических формул:

Годится, в последнем слагаемом подведём функцию под знак дифференциала:

Ответ: ![]()
Да, тяжеловато приходится со звёздами =)
Следующее задание для продвинутых студентов:
Пример 7
Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями 
Для его решения будет достаточно материалов, которые мы уже рассмотрели, но привычный путь весьма долог, и сейчас я расскажу ещё об одном эффективном методе. Идея на самом деле знакома из урока Вычисление площади с помощью определённого интеграла – это интегрирование по переменной «игрек» и использование формулы  . Подставляя в неё параметрические функции
. Подставляя в неё параметрические функции ![]() , получаем зеркальную рабочую формулу:
, получаем зеркальную рабочую формулу:

Действительно, ну а чем она хуже «стандартной»? В этом состоит ещё одно преимущество параметрической формы – уравнения ![]() способны исполнять роль не только «обычной»
способны исполнять роль не только «обычной» ![]() , но одновременно и обратной функции
, но одновременно и обратной функции ![]() .
.
В данном случае предполагается, что функции ![]() непрерывны на промежутке интегрирования и функция
непрерывны на промежутке интегрирования и функция ![]() монотонна на нём. Причём, если
монотонна на нём. Причём, если ![]() убывает на промежутке интегрирования (параметрические уравнения «прорисовывают» график «в противоход» (внимание!!) оси
убывает на промежутке интегрирования (параметрические уравнения «прорисовывают» график «в противоход» (внимание!!) оси ![]() ), то следует по уже рассмотренной технологии переставить пределы интегрирования либо изначально поставить «минус» перед интегралом.
), то следует по уже рассмотренной технологии переставить пределы интегрирования либо изначально поставить «минус» перед интегралом.
Решение и ответ Примера №7 в конце урока.
Заключительный мини-раздел посвящен более редкой задаче:
Как найти объем тела вращения,
если фигура ограничена параметрически заданной линией?
Актуализируем формулу, выведенную в начале урока:  . Общая методика решения точно такая же, как и при нахождении площади. Выдерну немногочисленные задачи из своей копилки:
. Общая методика решения точно такая же, как и при нахождении площади. Выдерну немногочисленные задачи из своей копилки:
Пример 8
Найти объем тела, образованного вращением вокруг оси ![]() криволинейной трапеции, ограниченной линией
криволинейной трапеции, ограниченной линией ![]() , если
, если ![]() .
.
Решение: всё подано в лучшем виде, осталось не оплошать в вычислениях:

Ответ: ![]()
Теперь ваш черёд:
Пример 9
Найти объем тела, образованного вращением вокруг оси ![]() эллипса
эллипса ![]()
Данная поверхность вращения называется эллипсоидом вращения или сфероидом.
А в случае равенства ![]() получится в точности сфера и, соответственно, объём ограниченного ей шара. Кстати, объём данного тела вращения довольно легко вычислить и в декартовых координатах, поскольку подынтегральная функция в формуле
получится в точности сфера и, соответственно, объём ограниченного ей шара. Кстати, объём данного тела вращения довольно легко вычислить и в декартовых координатах, поскольку подынтегральная функция в формуле  ликвидирует квадратный корень. Желающие могут выразить «игрек» из уравнения
ликвидирует квадратный корень. Желающие могут выразить «игрек» из уравнения ![]() и решить задание вторым способом.
и решить задание вторым способом.
Помимо простейших примеров вполне могут встретиться задачи, где придётся выполнить чертёж и находить объём тела вращения как разность объемов тел вращения (или наоборот, сумму), то есть использовать уже знакомые из статьи Объем тела вращения приёмы. Кроме того, по аналогии с предыдущим параграфом, легко вывести вторую формулу:  , с помощью которой рассчитывается объём тела вращения вокруг оси ординат. Но вероятность встретить такие вещи крайне мала, по крайне мере, лично я не припоминаю, что решал такие задания – вся надежда на вас =)
, с помощью которой рассчитывается объём тела вращения вокруг оси ординат. Но вероятность встретить такие вещи крайне мала, по крайне мере, лично я не припоминаю, что решал такие задания – вся надежда на вас =)
Желаю успехов!
Решения и ответы:
Пример 3: Решение: вычислим площадь первой арки циклоиды. Значение параметра изменяется в пределах ![]() .
.
Найдём производную: ![]() .
.
По формуле:

Ответ: ![]()
Пример 5: Решение: уравнения  задают окружность с центром в начале координат, радиуса
задают окружность с центром в начале координат, радиуса ![]() . Уравнение
. Уравнение ![]() определяет прямую, параллельную оси ординат. Поскольку
определяет прямую, параллельную оси ординат. Поскольку ![]() , то необходимо вычислить площадь заштрихованной на чертеже фигуры:
, то необходимо вычислить площадь заштрихованной на чертеже фигуры:
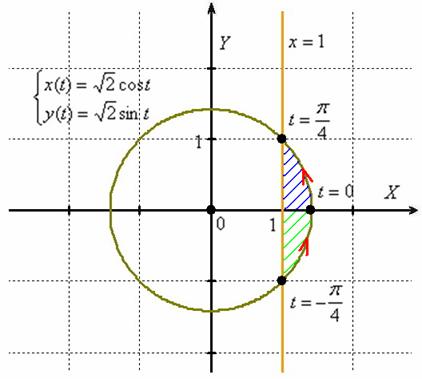
Найдём пределы изменения параметра, для этого подставим ![]() в параметрическое уравнение
в параметрическое уравнение ![]() :
:

Нижней точке соответствует значение ![]() , верхней точке – значение
, верхней точке – значение ![]() .
.
Так как фигура симметрична относительно оси ![]() , то вычислим площадь в верхней полуплоскости (синяя штриховка), а результат удвоим.
, то вычислим площадь в верхней полуплоскости (синяя штриховка), а результат удвоим.
Функция ![]() убывает на промежутке
убывает на промежутке ![]() , поэтому:
, поэтому:

Ответ: ![]()
Пример 7: Решение: выполним чертёж:
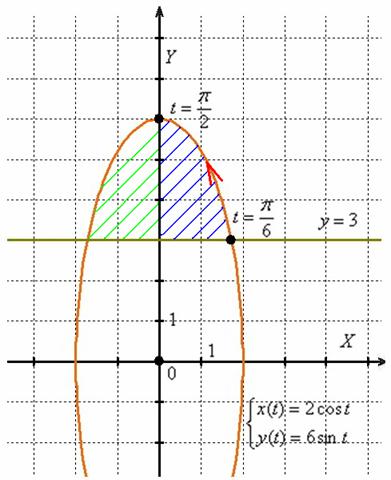
Фигура симметрична относительно оси ординат, вычислим часть площади в правой полуплоскости, результат удвоим. Найдём значения параметра, при которых эллипс пересекается с прямой ![]() . Для этого подставим
. Для этого подставим ![]() в параметрическое уравнение
в параметрическое уравнение ![]() :
:

(решения быстро отыскиваются по графику синуса либо тригонометрической таблице).
Подставим ![]() в параметрическое уравнение
в параметрическое уравнение ![]() :
:
![]() – таким образом, значение
– таким образом, значение ![]() задаёт правую (нужную нам) точку (поскольку получена именно её «иксовая» координата).
задаёт правую (нужную нам) точку (поскольку получена именно её «иксовая» координата).
Проверим, что очевидное значение ![]() задаёт верхнюю точку:
задаёт верхнюю точку:
 , что и требовалось проверить.
, что и требовалось проверить.
По формуле:

Примечание: в данном случае при изменении параметра от ![]() до
до ![]() направление «прорисовки» дуги совпадает с направлением оси ординат (так как
направление «прорисовки» дуги совпадает с направлением оси ординат (так как ![]() растёт), поэтому дополнительного вопроса с модификацией формулы не возникло.
растёт), поэтому дополнительного вопроса с модификацией формулы не возникло.
Ответ: ![]()
Пример 9: Решение: в силу симметрии эллипса, вычислим объём тела вращения в правой полуплоскости, результат удвоим. При изменении параметра в пределах ![]() функция
функция ![]() убывает, поэтому:
убывает, поэтому:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright