


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Нули функции. Интервалы знакопостоянства функции.
Метод интервалов
Значительная доля материала, касающегося производных и исследования функций, традиционно относится к школьной программе, и данная статья не является исключением из правила. Сегодня мы потренируемся в нахождении нулей и интервалов знакопостоянства функции, а также подробно разберём метод интервалов, который можно сравнить с надёжной арматурой в стенах рассматриваемой темы. Если же проект вашего здания находится на стадии котлована, пожалуйста, начните с вводного урока о графиках функций. Кроме того, желательно ознакомиться со статьями Область определения функции, Асимптоты графика, и, по существу, информация этой странички – логическое продолжение. Материал, естественно, будет полезен и старшеклассникам.
Открываем карты:
Что такое нули функции и что такое интервалы знакопостоянства функции?
Рассмотрим некоторую функцию ![]() .
.
1) Точки, в которых график ![]() пересекает ось
пересекает ось ![]() , называют нулями функции. Чтобы найти нули функции нужно решить уравнение
, называют нулями функции. Чтобы найти нули функции нужно решить уравнение ![]() , то есть найти те значения «икс», при которых функция обращается в ноль. В следующем условном примере нули функции
, то есть найти те значения «икс», при которых функция обращается в ноль. В следующем условном примере нули функции ![]() обозначены красными точками:
обозначены красными точками:
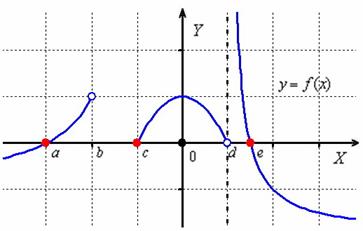
Очевидно, что ![]() . Заметьте, что точка
. Заметьте, что точка ![]() не является нулём функции, поскольку не входит в её область определения.
не является нулём функции, поскольку не входит в её область определения.
2) Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
В нашем случае функция положительна на интервалах ![]() , то есть для любого значения «икс» любого из перечисленных интервалов справедливо строгое неравенство
, то есть для любого значения «икс» любого из перечисленных интервалов справедливо строгое неравенство ![]() . Или совсем просто – график функции на таких интервалах расположен ВЫШЕ оси абсцисс.
. Или совсем просто – график функции на таких интервалах расположен ВЫШЕ оси абсцисс.
На интервалах ![]() функция отрицательна, то есть любому значению «икс», принадлежащему этим интервалам соответствует строгое неравенство
функция отрицательна, то есть любому значению «икс», принадлежащему этим интервалам соответствует строгое неравенство ![]() , и график функции расположен НИЖЕ оси
, и график функции расположен НИЖЕ оси ![]() .
.
Компактная запись перечисленных фактов выглядит так:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Строки можно переставить местами, это не имеет принципиального значения, лично я привык сначала указывать интервалы, на которых функция положительна.
Что можно сказать об интервале ![]() ? Только то, что функция не определена на данном интервале, и, разумеется, о знакопостоянстве речи не идёт вообще.
? Только то, что функция не определена на данном интервале, и, разумеется, о знакопостоянстве речи не идёт вообще.
Примечание: в математике более широким является термин «промежуток», который включает в себя не только интервал, но и полуинтервал либо отрезок. Полуинтервалы и отрезки знакопостоянства часто встречаются у кусочно-заданных функций. В частности, если на вышеуказанном чертеже «закрасить» точку с абсциссой ![]() , то получим промежуток (в данном случае – полуинтервал) знакопостоянства
, то получим промежуток (в данном случае – полуинтервал) знакопостоянства ![]() . Однако далее будут рассматриваться «обычные» функции, обладающие только интервалами знакопостоянства, поэтому в термине «промежуток знакопостоянства» нет особой нужды.
. Однако далее будут рассматриваться «обычные» функции, обладающие только интервалами знакопостоянства, поэтому в термине «промежуток знакопостоянства» нет особой нужды.
Как найти интервалы знакопостоянства функции?
Алгоритм метода интервалов прост и бесхитростен:
1) Находим область определения функции.
2) Находим нули функции (точки пересечения графика с осью абсцисс).
3) В большинстве заданий потребуется чертёж. Чертим ось ![]() и откладываем на ней точки разрыва (если они есть), а также нули функции (если они есть). Определяем знаки функции на интервалах, которые входят в область определения.
и откладываем на ней точки разрыва (если они есть), а также нули функции (если они есть). Определяем знаки функции на интервалах, которые входят в область определения.
Пункты можете законспектировать, впрочем, алгоритм очень быстро запомнит даже полный чайник. Тут всё прозрачно и логично.
Начнём с распространённой квадратичной функции:
Пример 1
Найти интервалы знакопостоянства функции.
![]()
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Таким образом, точки разрыва и «нехорошие» промежутки отсутствуют.
2) Найдём нули функции. Для этого нужно решить уравнение ![]() . В данном случае:
. В данном случае:
![]()
Дискриминант положителен, значит, уравнение имеет два действительных корня:
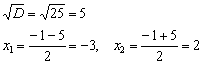
3) Откладываем все найденные точки на числовой оси:

В статье Область определения функции я выполнял подобные чертежи схематически, но сейчас для бОльшей наглядности изложения буду их масштабировать (за исключением клинических случаев). На том же уроке мы узнали, как выяснить знаки функции на интервалах – можно проанализировать расположение параболы. В данном случае ветви параболы направлены вверх, следовательно, на интервалах ![]() функция будет положительна:
функция будет положительна: ![]() . Попа параболы сидит на интервале
. Попа параболы сидит на интервале ![]() ниже оси абсцисс, и функция здесь отрицательна:
ниже оси абсцисс, и функция здесь отрицательна: ![]() .
.
Хорошо, параболу многие читатели представляют. Но что делать, если функция более сложная? Например, ![]() . Заметная часть аудитории уже затруднится сказать, как принципиально выглядит график данной функции. И это, так скажем, ещё только минимальное усложнение.
. Заметная часть аудитории уже затруднится сказать, как принципиально выглядит график данной функции. И это, так скажем, ещё только минимальное усложнение.
Однако и в простых и в сложных случаях работает универсальный способ:
Рассмотрим функцию ![]() непрерывную на некотором интервале
непрерывную на некотором интервале ![]() , график которой не пересекает ось
, график которой не пересекает ось ![]() на этом интервале. Тогда:
на этом интервале. Тогда:
– если функция ![]() положительна в какой-либо точке интервала
положительна в какой-либо точке интервала ![]() , то она положительна и ВО ВСЕХ точках данного интервала;
, то она положительна и ВО ВСЕХ точках данного интервала;
– если функция ![]() отрицательна в какой-либо точке интервала
отрицательна в какой-либо точке интервала ![]() , то она отрицательна и ВО ВСЕХ точках данного интервала.
, то она отрицательна и ВО ВСЕХ точках данного интервала.
Включите немного воображения: если на интервале нет точек разрыва, и график не пересекает ось абсцисс, то он не может по мановению волшебной палочки перескочить из нижней полуплоскости в верхнюю полуплоскость (или наоборот). Поэтому знак функции на таком интервале легко определить по одной-единственной точке.
Проведём небольшой эксперимент. Представьте, что вы совсем не знаете, как выглядит график функции ![]() и вам необходимо найти её интервалы знакопостоянства (кстати, если действительно не знаете, таки начертите многострадальную примадонну =)).
и вам необходимо найти её интервалы знакопостоянства (кстати, если действительно не знаете, таки начертите многострадальную примадонну =)).
1) Берём произвольную точку интервала ![]() . С вычислительной точки зрения проще всего взять
. С вычислительной точки зрения проще всего взять ![]() . Подставляем её в нашу функцию:
. Подставляем её в нашу функцию:
![]()
Следовательно, функция положительна и в каждой точке интервала ![]() .
.
2) Берём произвольную точку интервала ![]() , здесь по удобству вне конкуренции ноль. Снова выполняем подстановку:
, здесь по удобству вне конкуренции ноль. Снова выполняем подстановку:
![]()
А, значит, функция отрицательна и в каждой точке интервала ![]() .
.
3) И, наконец, обрабатываем наиболее простую точку интервала ![]() :
:
![]()
Поэтому функция положительна в каждой точке интервала ![]() .
.
Выполненные подстановки, вычисления почти всегда нетрудно выполнить устно, но в крайнем случае существует и черновик.
Фиксируем полученные результаты на числовой оси:

Да, вы не имеете никаких представлений о параболе, но совершенно точно можете сказать, что на интервалах ![]() график функции
график функции ![]() расположен ВЫШЕ оси
расположен ВЫШЕ оси ![]() , а на интервале
, а на интервале ![]() – НИЖЕ данной оси.
– НИЖЕ данной оси.
Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Точно так же решается целый спектр задач-«сателлитов», вот некоторые из них:
Решить квадратичное неравенство ![]() .
.
Проводим аналогичные действия и даём ответ ![]() .
.
Решить квадратичное неравенство ![]() .
.
Проводим аналогичные действия и даём ответ ![]() .
.
Найти область определения функции ![]() .
.
Проводим аналогичные действия, даём ответ ![]() .
.
И т.п.
Метод интервалов работает в самых примитивных случаях, например, для функции ![]() . Здесь прямая пересекает ось абсцисс в точке
. Здесь прямая пересекает ось абсцисс в точке ![]() , при этом слева от данной точки
, при этом слева от данной точки ![]() (график ниже оси
(график ниже оси ![]() ), а справа
), а справа ![]() (график выше оси
(график выше оси ![]() ). Тем не менее, для тех, кто в танке, задача разрешима и методом интервалов.
). Тем не менее, для тех, кто в танке, задача разрешима и методом интервалов.
Может ли функция быть положительно или отрицательной на всей числовой прямой? Конечно, в статье Область определения функции мы рассмотрели типовые примеры. В частности выяснили, что ![]() (парабола, полностью лежащая в верхней полуплоскости). Метод интервалов проходит и тут! Рассматриваем единственный интервал
(парабола, полностью лежащая в верхней полуплоскости). Метод интервалов проходит и тут! Рассматриваем единственный интервал ![]() , берём из него самую удобную точку
, берём из него самую удобную точку ![]() и выполняем подстановку:
и выполняем подстановку: ![]() . А значит, функция положительна и в каждой точке интервала
. А значит, функция положительна и в каждой точке интервала ![]() .
.
Перейдём к кубическим многочленам:
Пример 2
Найти интервалы знакопостоянства функции.
![]()
Решение: снова придерживаемся алгоритма:
1) Функция определена на всей числовой прямой.
2) Найдём нули функции, то есть решим уравнение ![]() . Для этого выполним разложение на множители:
. Для этого выполним разложение на множители:
![]()
Таким образом, нули функции: ![]() .
.
3) Откладываем найденные значения на числовой прямой:

Теперь в каждом из четырёх полученных интервалов берём наиболее простую точку и находим значения функции в данных точках:
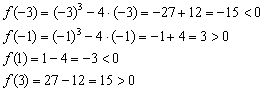
Таким образом:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Вы можете не знать, как выглядит график функции ![]() , но уже, по крайне мере, понятно, где он выше оси
, но уже, по крайне мере, понятно, где он выше оси ![]() , а где ниже.
, а где ниже.
Кубическая функция настолько распространена, что не удержусь от полного чертежа «молнии»:
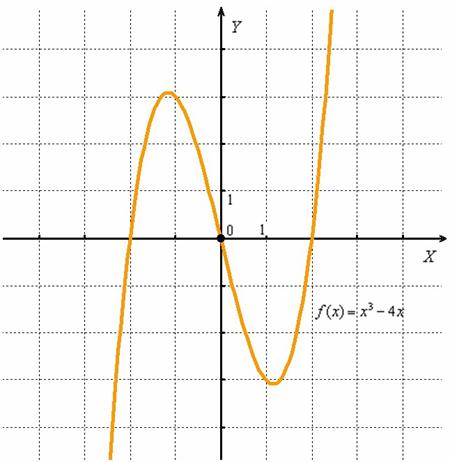
Казалось бы, решение можно упростить: взять левый интервал ![]() , выяснить, что на нём функция отрицательна, а дальше знаки будут чередоваться – «плюс», «минус», «плюс». Знакочередование бывает часто, но…
, выяснить, что на нём функция отрицательна, а дальше знаки будут чередоваться – «плюс», «минус», «плюс». Знакочередование бывает часто, но…
ЗНАКИ ЧЕРЕДУЮТСЯ ДАЛЕКО НЕ ВСЕГДА
Поэтому не ленимся – ТЕРПЕЛИВО рассматриваем КАЖДЫЙ интервал: из КАЖДОГО интервала берём наиболее выгодную точку и выясняем знак функции в данной точке.
Вот простой пример, когда интервала два, но знакочередования нет: ![]() . Экспонента всегда положительна
. Экспонента всегда положительна ![]() , квадрат неотрицателен
, квадрат неотрицателен ![]() , поэтому вся функция неотрицательна:
, поэтому вся функция неотрицательна: ![]() , очевидно, достигая нуля в единственной точке
, очевидно, достигая нуля в единственной точке ![]() . Такого решения будет вполне достаточно. Не обязательно чертить координатную ось! Обратите внимание, здесь есть тонкость при записи ответа:
. Такого решения будет вполне достаточно. Не обязательно чертить координатную ось! Обратите внимание, здесь есть тонкость при записи ответа:
![]() , если
, если ![]() .
.
То есть, функция положительна везде, кроме точки ноль.
Но формально можно использовать метод интервалов, который приведёт нас к такому же результату:

Если честно, не помню, как выглядит чертёж, однако совершенно точно можно сказать, что график данной функции лежит в верхней полуплоскости и касается оси абсцисс в точке ![]() .
.
Или парабола, касающаяся оси, например: ![]() . Такая же история. Кстати, если вы внимательно изучили геометрические преобразования графиков, то сразу поймёте, как расположена данная парабола.
. Такая же история. Кстати, если вы внимательно изучили геометрические преобразования графиков, то сразу поймёте, как расположена данная парабола.
Следует отметить, что ситуация касания графика оси не единственна, в ряде случаев функция не меняет знак при переходе через точку разрыва. Хороший пример встретился в статье Непрерывность функции: ![]() .
.
Пример 3
Найти интервалы знакопостоянства функции.
![]()
Это пример для самостоятельного решения. После того, как определите знаки на интервалах, попытайтесь представить, как выглядит данная «молния». Примерный образец чистового оформления задания в конце урока.
Функции с многочленами встречаются очень часто, поэтому имеет смысл рассмотреть ещё пару экземпляров:
Пример 4
Найти интервалы знакопостоянства функции.
![]()
Решение:
1) Функция определена на всей числовой прямой.
2) Находим нули функции:
![]()
Таким образом, нули функции: ![]() .
.
3) Откладываем данные значения на оси абсцисс:

Определим знаки функции на полученных интервалах:
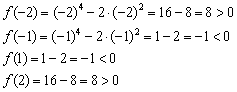
Таким образом:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Читатели с высоким и средним уровнем подготовки могут укоротить процесс решения, используя чётность/нечётность функций, чайникам же рекомендую не торопиться и тщательно прорабатывать каждый пункт решения.
Функция-многочлен 4-й степени тоже достойна полного графика:
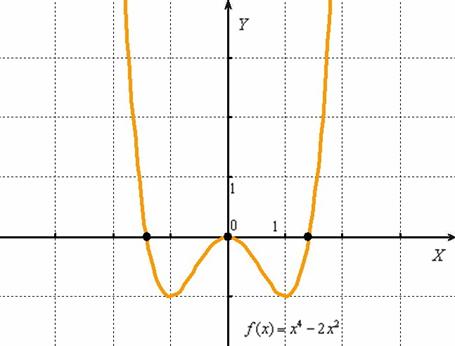
Собрат для самостоятельного решения:
Пример 5
Найти интервалы знакопостоянства функции.
![]()
В ходе выполнения задания потребуется решить так называемое биквадратное уравнение, которое также рассматривается в школьном курсе математики. В данном примере необходимо провести замену ![]() , разобраться с уравнением
, разобраться с уравнением ![]() , найти корни
, найти корни ![]() и на финише из равенств
и на финише из равенств ![]() получить 4 корня. Полное решение и ответ в конце урока.
получить 4 корня. Полное решение и ответ в конце урока.
Перейдём к обширной группе функций, у которых есть точки разрыва:
Пример 6
Найти интервалы знакопостоянства функции.
![]()
Решение: вот здесь начинает в полную силу работать пункт № 1 алгоритма:
1) Функция определена на всей числовой прямой, кроме точки ![]() , которая обращает знаменатель в ноль.
, которая обращает знаменатель в ноль.
2) Находим точки пресечения графика с осью ![]() (нули функции):
(нули функции):
![]()
Знаменатель нулевым быть не может, поэтому приравниваем к нулю числитель и решаем уравнение счастливого первоклассника:
![]()
3) Откладываем на оси абсцисс ВСЕ найденные точки, при этом выкалываем точку ![]() , так как она не входит в область определения функции:
, так как она не входит в область определения функции:

Определим знаки функции на полученных интервалах:
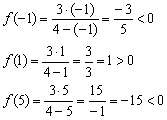
В результате:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Чем отличается данный пример от всех предыдущих? Да ничем особенным.
Напоминаю, что практически так же решается ряд смежных задач, например:
Решить неравенство ![]()
Ответ: ![]()
Решить неравенство ![]()
Ответ: ![]()
Найти область определения функции ![]()
Ответ: ![]()
И т.д.
Короткое разминочное задание для самостоятельного решения:
Пример 7
Найти интервалы знакопостоянства функции.
![]()
Кстати, подобные вещи вполне реально решить мысленно! Попытайтесь найти интервалы знакопостоянства «в уме», тем более, вы ничем не рискуете – в конце урока есть готовый образец.
Рассмотрим более навороченные дробно-рациональные функции:
Пример 8
Найти интервалы знакопостоянства функции.
![]()
Решение: далее пункты алгоритма нумеровать не будем.
Находим область определения функции. Проверим, обращается ли знаменатель в ноль:
![]()
Перепишем квадратное уравнение в привычном виде:
![]()
И для удобства сменим знаки у каждого слагаемого:
![]()
!!! Внимание: в САМОЙ ФУНКЦИИ так делать НЕЛЬЗЯ! В ней знак «минус» не пропадает: ![]() .
.
![]()
Дискриминант больше нуля, значит, уравнение имеет два действительных корня и в область определения не войдут две точки:
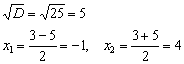
Найдём точки пересечения графика с осью абсцисс: ![]() . Нулевым может быть только числитель, поэтому рассматриваем уравнение
. Нулевым может быть только числитель, поэтому рассматриваем уравнение ![]() . Решение можно провести через дискриминант, однако нетрудно заметить, что у нас квадрат разности:
. Решение можно провести через дискриминант, однако нетрудно заметить, что у нас квадрат разности:
![]()
Таким образом, функция обращается в ноль в единственной точке: ![]()
Используя уже наработанный алгоритм, определим знаки функции на полученных интервалах:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Как выглядит график функции, знают немногие, но совершенно точно можно сказать, что на интервалах ![]() он расположен ВЫШЕ оси
он расположен ВЫШЕ оси ![]() , а на интервалах
, а на интервалах ![]() – НИЖЕ данной оси. В точке
– НИЖЕ данной оси. В точке ![]() график, кстати, только касается её.
график, кстати, только касается её.
Пример 9
Найти интервалы знакопостоянства функции.
![]()
Это пример для самостоятельного решения.
Заключительные примеры посвящены функциям, в которые входит натуральный логарифм:
Пример 10
Найти интервалы знакопостоянства функции.
![]()
Просто и со вкусом.
Решение: функция определена и непрерывна на интервале ![]() . Найдём точки пересечения графика с осью абсцисс:
. Найдём точки пересечения графика с осью абсцисс:
![]()
Нулю может быть равен только числитель:
![]()
Согласно определению логарифма (которое нужно бы уже хорошо усвоить):
![]()
Отметим найденные точки на числовой прямой:

На промежутке ![]() функция не определена вообще. Об этом можно сделать пометку на чертеже либо просто оставить полуинтервал без внимания. Я обычно не ставлю никаких знаков.
функция не определена вообще. Об этом можно сделать пометку на чертеже либо просто оставить полуинтервал без внимания. Я обычно не ставлю никаких знаков.
Определим знаки на интервалах, которые входят в область определения функции:
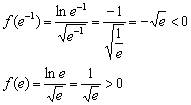
Таким образом:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
На практике под логарифмом часто находится квадратный дву- или трёхчлен. Пожалуйста, ВНИМАТЕЛЬНО изучите оставшиеся примеры, в которых метод интервалов используется ДВАЖДЫ: первый раз для нахождения области определения, а второй раз для нахождения интервалов знакопостоянства.
Пример 11
Найти интервалы знакопостоянства функции.
![]()
Решение: сначала найдём область определения функции. Выражение под знаком логарифма должно быть положительным:
![]()
Квадратичное неравенство решим методом интервалов. Проверим, существуют ли действительные корни соответствующего уравнения:
![]()
Да, уравнение имеет два действительных перца. Не нужно удивляться, что дискриминант получился «плохой», это довольно распространённый инцидент в ходе исследовании функций. Невозмутимо находим корни:
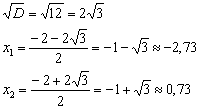
Откладываем найденные точки на числовой прямой. Их следует выколоть, поскольку неравенство строгое. Далее стандартно из каждого интервала выбираем наиболее простую точку, и определяем знаки функции ![]() на полученных интервалах:
на полученных интервалах:
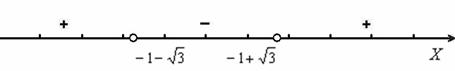
Таким образом, область определения:
![]()
Что теперь? Теперь ЗАБЫВАЕМ про найденные знаки и интервалы знакопостоянства. Самый важный факт состоит в том, что отрезок ![]() не входит в область определения функции
не входит в область определения функции ![]() .
.
На втором шаге находим точки пересечения графика с осью абсцисс (нули функции):
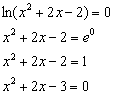
Решаем ещё одно квадратное уравнение:
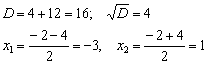
Снова используем метод интервалов. Откладываем на числовой прямой ВСЕ найдённые ранее точки:
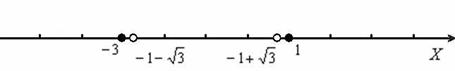
Тесновато получилось, но что делать, зато масштаб выдержан.
Определяем знаки функции на интервалах, при этом не забываем, что отрезок посередине не входит в область определения, и возиться с ним не надо! Но от этого, увы, не легче, так как подстановка будет брутальной. Придётся тыкать по клавишам калькулятора:
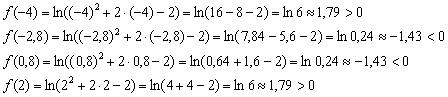
Таким образом:
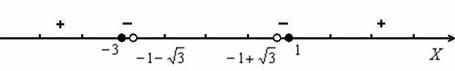
Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Что можно сказать о графике функции ![]() ? На отрезке
? На отрезке ![]() его не существует вообще, на крайних интервалах он расположен выше оси
его не существует вообще, на крайних интервалах он расположен выше оси ![]() , на маленьких интервалах – ниже данной оси, точки пересечения с осью:
, на маленьких интервалах – ниже данной оси, точки пересечения с осью: ![]() .
.
Пример 12
Найти интервалы знакопостоянства функции.
![]()
Это пример для самостоятельного изучения. На первом шаге решение можно ускорить – неравенство ![]() значительно выгоднее решить аналитически, нежели использовать метод интервалов. Данный способ подробно рассмотрен на уроке Область определения функции.
значительно выгоднее решить аналитически, нежели использовать метод интервалов. Данный способ подробно рассмотрен на уроке Область определения функции.
Вот, пожалуй, и все основные задания по теме, которые встречаются на практике в ходе полного исследования функции. Хочется привести примеры сложнее, но они будут в известной степени надуманы.
Желаю успехов!
Решения и ответы:
Пример 3: Решение:
1) Функция определена на всей числовой прямой.
2) Найдём нули функции:
![]()
Таким образом: ![]() .
.
3) Определим знаки функции методом интервалов:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Пример 5: Решение:
1) Функция определена на всей числовой прямой
2) Найдём нули функции:
![]()
Проведём замену: ![]()
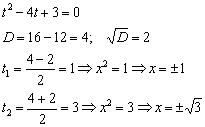
3) Выполним чертёж и определим знаки функции на найденных интервалах:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Пример 7: Решение:
1) Функция определена на всей числовой прямой, кроме точки ![]() .
.
2) Найдём нули функции:
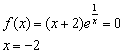
3) Определим знаки функции на полученных интервалах:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Пример 9: Решение: точки ![]() не входят в область определения функции.
не входят в область определения функции.
График функции не пересекает ось ![]() , т.к.
, т.к. ![]()
Методом интервалов определим знаки функции:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Пример 12: Решение: найдём область определения:
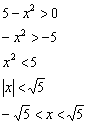
Таким образом, ![]()
Найдём точки пересечения графика с осью абсцисс:
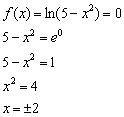
Определим знаки функции на полученных интервалах:

Ответ:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright