Высшая математика для чайников, или с чего начать?
Повторяем школьный курс

Аналитическая геометрия:

Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида

Элементы высшей алгебры:

Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы

Пределы:

Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория

Производные функций:

Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных

Функции и графики:

Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи

ФНП:

Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов

Интегралы:

Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:

Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты

Числовые ряды:

Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности

Функциональные ряды:

Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений

Кратные интегралы:

Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы

Элементы векторного анализа:

Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса

Комплексный анализ:

ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?

Теория вероятностей:

Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ

Математическая статистика:

Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Пример 1

Исследовать ряд на сходимость
Мы видим, что в общем члене ряда у нас есть , а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.

Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.
(1) Составляем отношение следующего члена ряда к предыдущему: . Из условия мы видим, что общий член ряда . Для того, чтобы получить следующий член ряда нужно ВМЕСТО  подставить : .
(2) Избавляемся от четырехэтажности дроби. При определенном опыте решения этот шаг можно пропускать.
(3) В числителе раскрываем скобки. В знаменателе выносим четверку из степени.
(4) Сокращаем на . Константу  выносим за знак предела. В числителе в скобках приводим подобные слагаемые.
(5) Неопределенность  устраняется стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.
(6) Почленно делим числители на знаменатели, и указываем слагаемые, которые стремятся к нулю.
(7) Упрощаем ответ и делаем пометку, что  с выводом о том, что, по признаку Даламбера исследуемый ряд сходится.

В рассмотренном примере в общем члене ряда у нас встретился многочлен 2-й степени. Что делать, если там многочлен 3-й, 4-й или более высокой степени? Дело в том, что если дан многочлен более высокой степени, то возникнут трудности с раскрытием скобок. В этом случае можно применять «турбо»-метод решения.

Пример 2

Возьмём похожий ряд и исследуем его на сходимость

Сначала полное решение, потом комментарии:

Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.

(1) Составляем отношение .
(2) Избавляемся от четырехэтажности дроби.

(3) Рассмотрим выражение  в числителе и выражение  в знаменателе. Мы видим, что в числителе нужно раскрывать скобки и возводить в четвертую степень: , чего делать совершенно не хочется. А для тех, кто не знаком с биномом Ньютона, эта задача окажется ещё сложнее. Проанализируем старшие степени: если мы вверху раскроем скобки , то получим старшую степень . Внизу у нас такая же старшая степень: . По аналогии с предыдущим примером, очевидно, что при почленном делении числителя и знаменателя на  у нас в пределе получится единица. Или, как говорят математики, многочлены   и  – одного порядка роста. Таким образом, вполне можно обвести отношение  простым карандашом и сразу указать, что эта штука стремится к единице. Аналогично расправляемся со второй парой многочленов:  и , они тоже одного порядка роста, и их отношение стремится к единице.

На самом деле, такую «халтуру» можно было провернуть и в Примере № 1, но для многочлена 2-й степени такое решение смотрится всё-таки как-то несолидно. Лично я поступаю так: если есть многочлен (или многочлены) первой или второй степени, я использую «длинный» способ решения Примера 1. Если попадается многочлен 3-й и более высоких степеней, я использую «турбо»-метод по образцу Примера 2.

Пример 3

Исследовать ряд на сходимость

Полное решение и образец оформления в конце урока

Рассмотрим типовые примеры с факториалами:

Пример 4

Исследовать ряд на сходимость

В общий член ряда входит и степень, и факториал. Ясно, как день, что здесь надо использовать признак Даламбера. Решаем.

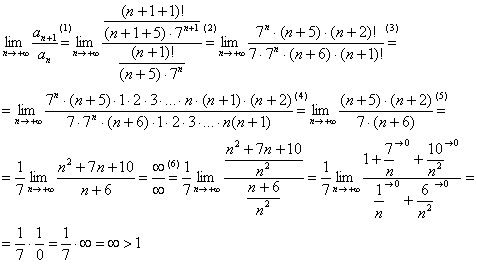
Таким образом, исследуемый ряд расходится.
(1) Составляем отношение . Повторяем еще раз. По условию общий член ряда: . Для того чтобы получить следующий член ряда, вместо  нужно подставить , таким образом: .
(2) Избавляемся от четырехэтажности дроби.
(3) Отщипываем семерку от степени. Факториалы расписываем подробно. Как это сделать – см. начало урока или статью о числовых последовательностях.
(4) Сокращаем всё, что можно сократить.
(5) Константу  выносим за знак предела. В числителе раскрываем скобки.
(6) Неопределенность  устраняем стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.

Пример 5

Исследовать ряд на сходимость

Полное решение и образец оформления в конце урока

Пример 6

Исследовать ряд на сходимость

Иногда встречаются ряды, которые в своей начинке содержат «цепь» множителей, этот тип ряда мы еще не рассматривали. Как исследовать ряд с «цепочкой» множителей? Использовать признак Даламбера. Но сначала для понимания происходящего распишем ряд подробно:

Из разложения мы видим, что у каждого следующего члена ряда добавляется дополнительный множитель в знаменателе, поэтому, если общий член ряда , то  следующий член ряда:
. Вот здесь часто автоматом допускают ошибку, формально по алгоритму записывая, что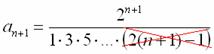

Примерный образец решения может выглядеть так:

Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.

Пример 7

Исследовать ряд на сходимость

Мы видим, что дробь полностью находится под степенью, зависящей от «эн», а значит, нужно использовать радикальный признак Коши:

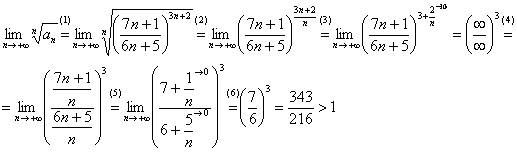
Таким образом, исследуемый ряд расходится.

(1) Оформляем общий член ряда под корень.

(2) Переписываем то же самое, только уже без корня, используя свойство степеней .
(3) В показателе почленно делим числитель на знаменатель, указывая, что
(4) В результате у нас получилась неопределенность . Здесь можно было пойти длинным путем: возвести  в куб, возвести  в куб, потом разделить числитель и знаменатель на «эн» в кубе. Но в данном случае есть более эффективное решение: этот приём можно использовать прямо под степенью-константой. Для устранения неопределенности делим числитель и знаменатель на  (старшую степень многочленов).

(5) Выполняем почленное деление, и указываем слагаемые, которые стремятся к нулю.
(6) Доводим ответ до ума, помечаем, что  и делаем вывод о том, что ряд расходится.

А вот более простой пример для самостоятельного решения:

Пример 8

Исследовать ряд на сходимость

И еще пара типовых примеров.

Полное решение и образец оформления в конце урока

Пример 9

Исследовать ряд на сходимость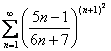
Используем радикальный признак Коши:

Таким образом, исследуемый ряд сходится.

(1) Помещаем общий член ряда под корень.

(2) Переписываем то же самое, но уже без корня, при этом раскрываем скобки, используя формулу сокращенного умножения: .
(3) В показателе почленно делим числитель на знаменатель и указываем, что .
(4) Получена неопределенность вида , и здесь тоже можно выполнять деление прямо под степенью. Но с одним условием: коэффициенты при старших степенях многочленов должны быть разными. У нас они разные (5 и 6), и поэтому можно (и нужно) разделить оба этажа на . Если же эти коэффициенты одинаковы, например (1 и 1): , то такой фокус не проходит и нужно использовать второй замечательный предел. Если помните, эти тонкости рассматривались в последнем параграфе статьи Методы решения пределов.

(5) Собственно выполняем почленное деление и указываем, какие слагаемые у нас стремятся к нулю.
(6) Неопределенность устранена, у нас остался простейший предел: . Почему  в бесконечно большой степени стремится к нулю? Потому что основание степени удовлетворяет неравенству . Если у кого есть сомнения в справедливости предела , то я не поленюсь, возьму в руки калькулятор:
Если , то
Если , то
Если , то
Если , то
Если , то
… и т.д. до бесконечности – то есть, в пределе:

Прямо таки бесконечно убывающая геометрическая прогрессия на пальцах =)
! Никогда не используйте этот приём в качестве доказательства! Ибо если что-то очевидно, то это ещё не значит, что это правильно.

(7) Указываем, что  и делаем вывод о том, что ряд сходится.

Пример 10

Исследовать ряд на сходимость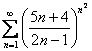

Это пример для самостоятельного решения.

Пример 11

Исследовать ряд на сходимость

Почти классика. Натуральный логарифм и какая-нибудь бяка.

Основной предпосылкой использования интегрального признака Коши является тот факт, что в общем члене ряда содержатся множители, похожие на некоторую функцию и её производную. Из темы Производная вы наверняка запомнили простейшую табличную вещь: , и у нас как раз такой каноничный случай.

Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: . Затем под интегралом переписываем «начинку» ряда с буковкой «хэ»: . Чего-то не хватает…, ах, да, еще в числителе нужно прилепить значок дифференциала: .

Теперь нужно вычислить несобственный интеграл . При этом возможно два случая:

1) Если выяснится, что интеграл  сходится, то будет сходиться и наш ряд .

2) Если выяснится, что интеграл   расходится, то наш ряд  тоже будет расходиться.

Повторюсь, если материал запущен, то чтение параграфа будет трудным и малопонятным, поскольку применение признака по сути дела сводится к вычислению несобственного интеграла первого рода.

Полное решение и оформление примера должно выглядеть примерно так:

Используем интегральный признак:

Подынтегральная функция непрерывна на

Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.

Пример 12

Исследовать ряд на сходимость

Решение и образец оформления в конце урока

В рассмотренных примерах логарифм также мог находиться под корнем, это не изменило бы способа решения.

И еще два примера на закуску

Пример 13

Исследовать ряд на сходимость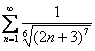

По общим «параметрам» общий член ряда подходит для использования предельного признака сравнения. Нужно всего лишь раскрыть скобки  и сразу сдать на кандидата предельно сравнить данный ряд со сходящимся рядом . Впрочем, я немного слукавил, скобки можно и не раскрывать, но всё равно решение через предельный признак будет выглядеть несколько вычурно.

Поэтому мы используем интегральный признак Коши:

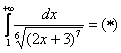
Подынтегральная функция непрерывна на

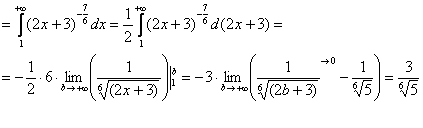
Получено конечное число, значит, исследуемый ряд  сходится вместе с соответствующим несобственным интегралом.

! Примечание: полученное число  –  не является суммой ряда!!!

Пример 14

Исследовать ряд на сходимость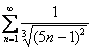

Решение и образец оформления в конце урока, который подходит к концу.

Пример 3: Используем признак Даламбера:

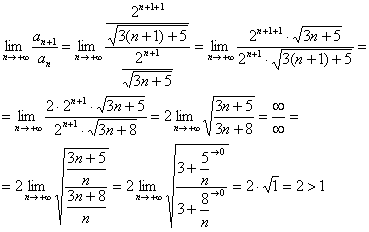
Таким образом, исследуемый ряд расходится.

Примечание: Можно было использовать и «турбо»-метод решения: сразу обвести карандашом отношение , указать, что оно стремится к единице и сделать пометку: «одного порядка роста».

Пример 5: Используем признак Даламбера:

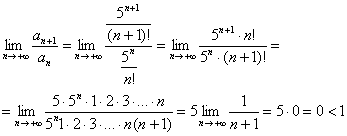
Таким образом, исследуемый ряд сходится.

Пример 8: Используем радикальный признак Коши:

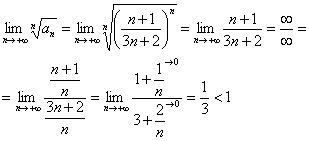
Таким образом, исследуемый ряд сходится.

Пример 10: Используем радикальный признак Коши:

Таким образом, исследуемый ряд расходится.
Примечание: Здесь основание степени , поэтому

Пример 12: Используем интегральный признак:.
 
Подынтегральная функция непрерывна на .

Получено конечное число, значит, исследуемый ряд  сходится вместе с соответствующим несобственным интегралом.

Пример 14: Используем интегральный признак:
 
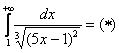
Подынтегральная функция непрерывна на .

Таким образом, исследуемый ряд  расходится вместе с соответствующим несобственным интегралом.

Примечание: Ряд 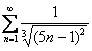 также можно исследовать с помощью предельного признака сравнения. Для этого удобно раскрыть скобки под корнем   и сравнить исследуемый ряд с расходящимся рядом .