


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Тройные интегралы. Вычисление объема тела.
Тройной интеграл в цилиндрических координатах
Три дня в деканате покойник лежал, в штаны Пифагора одетый,
В руках Фихтенгольца он томик держал, что сжил его с белого света,
К ногам привязали тройной интеграл, и в матрицу труп обернули,
А вместо молитвы какой-то нахал прочёл теорему Бернулли.
Тройные интегралы – это то, чего уже можно не бояться =) Ибо если Вы читаете сей текст, то, скорее всего, неплохо разобрались с теорией и практикой «обычных» интегралов, а также двойными интегралами. А там, где двойной, неподалёку и тройной:
![]()
И в самом деле, чего тут опасаться? Интегралом меньше, интегралом больше….
Разбираемся в записи:
![]() – значок тройного интеграла;
– значок тройного интеграла;
![]() – подынтегральная функция трёх переменных;
– подынтегральная функция трёх переменных;
![]() – произведение дифференциалов.
– произведение дифференциалов.
![]() – область интегрирования.
– область интегрирования.
Особо остановимся на области интегрирования. Если в двойном интеграле она представляет собой плоскую фигуру, то здесь – пространственное тело, которое, как известно, ограничено множеством поверхностей. Таким образом, помимо вышеуказанного вы должны ориентироваться в основных поверхностях пространства и уметь выполнять простейшие трёхмерные чертежи.
Некоторые приуныли, понимаю…. Увы, статью нельзя озаглавить «тройные интегралы для чайников», и кое-что знать/уметь нужно. Но ничего страшного – весь материал изложен в предельно доступной форме и осваивается в кратчайшие сроки!
Что значит вычислить тройной интеграл и что это вообще такое?
Вычислить тройной интеграл – это значит найти ЧИСЛО:
![]()
В простейшем случае, когда ![]() , тройной интеграл
, тройной интеграл ![]() численно равен объёму тела
численно равен объёму тела ![]() . И действительно, в соответствии с общим смыслом интегрирования, произведение
. И действительно, в соответствии с общим смыслом интегрирования, произведение ![]() равно бесконечно малому объёму
равно бесконечно малому объёму ![]() элементарного «кирпичика» тела. А тройной интеграл как раз и объединяет все эти бесконечно малые частички по области
элементарного «кирпичика» тела. А тройной интеграл как раз и объединяет все эти бесконечно малые частички по области ![]() , в результате чего получается интегральное (суммарное) значение объёма тела:
, в результате чего получается интегральное (суммарное) значение объёма тела: ![]() .
.
Кроме того, у тройного интеграла есть важные физические приложения. Но об этом позже – во 2-й части урока, посвящённой вычислениям произвольных тройных интегралов, у которых функция ![]() в общем случае отлична от константы и непрерывна в области
в общем случае отлична от константы и непрерывна в области ![]() . В данной же статье детально рассмотрим задачу нахождения объёма, которая по моей субъективной оценке встречается в 6-7 раз чаще.
. В данной же статье детально рассмотрим задачу нахождения объёма, которая по моей субъективной оценке встречается в 6-7 раз чаще.
Как решить тройной интеграл?
Ответ логично вытекает из предыдущего пункта. Необходимо определить порядок обхода тела и перейти к повторным интегралам. После чего последовательно расправиться с тремя одиночными интегралами.
Как видите, вся кухня очень и очень напоминает двойные интегралы, с тем отличием, что сейчас у нас добавилась дополнительная размерность (грубо говоря, высота). И, наверное, многие из вас уже догадались, как решаются тройные интегралы.
Развеем оставшиеся сомнения:
Пример 1
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями
![]()
Пожалуйста, перепишите столбиком на бумагу:
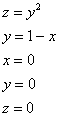
И ответьте на следующие вопросы. Знаете ли Вы, какие поверхности задают эти уравнения? Понятен ли Вам неформальный смысл этих уравнений? Представляете ли Вы, как данные поверхности расположены в пространстве?
Если Вы склоняетесь к общему ответу «скорее нет, чем да», то обязательно проработайте урок Основные поверхности пространства, иначе дальше будет не продвинуться!
Решение: используем формулу ![]() .
.
Для того чтобы выяснить порядок обхода тела и перейти к повторным интегралам нужно (всё гениальное просто) понять, что это за тело. И такому пониманию во многих случаях здОрово способствуют чертежи.
По условию, тело ограничено несколькими поверхностями. С чего начать построение? Предлагаю следующий порядок действий:
Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость ![]() . Первый раз сказал, как эта проекция называется, lol =)
. Первый раз сказал, как эта проекция называется, lol =)
Коль скоро проецирование проводится вдоль оси ![]() , то в первую очередь целесообразно разобраться с поверхностями, которые параллельны данной оси. Напоминаю, что уравнения таких поверхностей не содержат буквы «зет». В рассматриваемой задаче их три:
, то в первую очередь целесообразно разобраться с поверхностями, которые параллельны данной оси. Напоминаю, что уравнения таких поверхностей не содержат буквы «зет». В рассматриваемой задаче их три:
– уравнение ![]() задаёт координатную плоскость
задаёт координатную плоскость ![]() , которая проходит через ось
, которая проходит через ось ![]() ;
;
– уравнение ![]() задаёт координатную плоскость
задаёт координатную плоскость ![]() , которая проходит через ось
, которая проходит через ось ![]() ;
;
– уравнение ![]() задаёт плоскость, проходящую через «одноимённую» «плоскую» прямую параллельно оси
задаёт плоскость, проходящую через «одноимённую» «плоскую» прямую параллельно оси ![]() .
.
Скорее всего, искомая проекция представляет собой следующий треугольник:
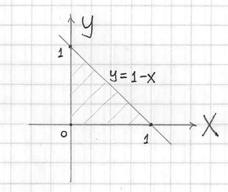
Возможно, не все до конца поняли, о чём речь. Представьте, что из экрана монитора выходит ось ![]() и утыкается прямо в вашу переносицу (т.е. получается, что вы смотрите на 3-мерный чертёж сверху). Исследуемое пространственное тело находится в бесконечном трёхгранном «коридоре» и его проекция на плоскость
и утыкается прямо в вашу переносицу (т.е. получается, что вы смотрите на 3-мерный чертёж сверху). Исследуемое пространственное тело находится в бесконечном трёхгранном «коридоре» и его проекция на плоскость ![]() , вероятнее всего, представляет собой заштрихованный треугольник.
, вероятнее всего, представляет собой заштрихованный треугольник.
Обращаю особое внимание, что пока мы высказали лишь предположение о проекции и оговорки «скорее всего», «вероятнее всего» были не случайны. Дело в том, что проанализированы ещё не все поверхности и может статься так, что какая-нибудь из них «оттяпает» часть треугольника. В качестве наглядного примера напрашивается сфера с центром в начале координат радиусом мЕньшим единицы, например, сфера ![]() – её проекция на плоскость
– её проекция на плоскость ![]() (круг
(круг ![]() ) не полностью «накроет» заштрихованную область, и итоговая проекция тела будет вовсе не треугольником (круг «срежет» ему острые углы).
) не полностью «накроет» заштрихованную область, и итоговая проекция тела будет вовсе не треугольником (круг «срежет» ему острые углы).
На втором этапе выясняем, чем тело ограничено сверху, чем снизу и выполняем пространственный чертёж. Возвращаемся к условию задачи и смотрим, какие поверхности остались. Уравнение ![]() задаёт саму координатную плоскость
задаёт саму координатную плоскость ![]() , а уравнение
, а уравнение ![]() – параболический цилиндр, расположенный над плоскостью
– параболический цилиндр, расположенный над плоскостью ![]() и проходящий через ось
и проходящий через ось ![]() . Таким образом, проекция тела действительно представляет собой треугольник.
. Таким образом, проекция тела действительно представляет собой треугольник.
Кстати, здесь обнаружилась избыточность условия – в него было не обязательно включать уравнение плоскости ![]() , поскольку поверхность
, поскольку поверхность ![]() , касаясь оси абсцисс, и так замыкает тело. Интересно отметить, что в этом случае мы бы не сразу смогли начертить проекцию – треугольник «прорисовался» бы только после анализа уравнения
, касаясь оси абсцисс, и так замыкает тело. Интересно отметить, что в этом случае мы бы не сразу смогли начертить проекцию – треугольник «прорисовался» бы только после анализа уравнения ![]() .
.
Аккуратно изобразим фрагмент параболического цилиндра и искомое тело:
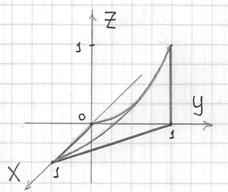
После выполнения чертежей с порядком обхода тела никаких проблем!
Сначала определим порядок обхода проекции (при этом ГОРАЗДО УДОБНЕЕ ориентироваться по двумерному чертежу). Это делается АБСОЛЮТНО ТАК ЖЕ, как и в двойных интегралах! Вспоминаем лазерную указку и сканирование плоской области. Выберем «традиционный» 1-й способ обхода:
![]()
Далее берём в руки волшебный фонарик, смотрим на трёхмерный чертёж и строго снизу вверх просвечиваем пациента. Лучи входят в тело через плоскость ![]() и выходят из него через поверхность
и выходят из него через поверхность ![]() . Таким образом, порядок обхода тела:
. Таким образом, порядок обхода тела:
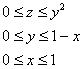
Перейдём к повторным интегралам:
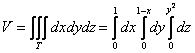
С интегралами опять рекомендую разбираться по отдельности:
1) Начать следует с «зетового» интеграла. Используем формулу Ньютона-Лейбница:
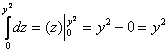
Подставим результат в «игрековый» интеграл:
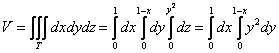
Что получилось? По существу решение свелось к двойному интегралу, и именно – к формуле ![]() объёма цилиндрического бруса! Дальнейшее хорошо знакомо:
объёма цилиндрического бруса! Дальнейшее хорошо знакомо:
2) 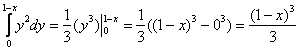
3) 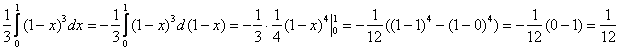
Обратите внимание на рациональную технику решения 3-го интеграла.
Ответ: ![]()
Вычисления всегда можно записать и «одной строкой»:
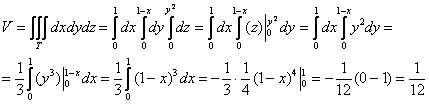
Но с этим способом будьте осторожнее – выигрыш в скорости чреват потерей качества, и чем труднее пример, тем больше шансов допустить ошибку.
Ответим на важный вопрос:
Нужно ли делать чертежи, если условие задачи не требует их выполнения?
Можно пойти четырьмя путями:
1) Изобразить проекцию и само тело. Это самый выигрышный вариант – если есть возможность выполнить два приличных чертежа, не ленитесь, делайте оба чертежа. Рекомендую в первую очередь.
2) Изобразить только тело. Годится, когда у тела несложная и очевидная проекция. Так, например, в разобранном примере хватило бы и трёхмерного чертежа. Однако тут есть и минус – по 3D-картинке неудобно определять порядок обхода проекции, и этот способ я бы советовал только людям с хорошим уровнем подготовки.
3) Изобразить только проекцию. Тоже неплохо, но тогда обязательны дополнительные письменные комментарии, чем ограничена область с различных сторон. К сожалению, третий вариант зачастую бывает вынужденным – когда тело слишком велико либо его построение сопряжено с иными трудностями. И такие примеры мы тоже рассмотрим.
4) Обойтись вообще без чертежей. В этом случае нужно представлять тело мысленно и закомментировать его форму/расположение письменно. Подходит для совсем простых тел либо задач, где выполнение обоих чертежей затруднительно. Но всё же лучше сделать хотя бы схематический рисунок, поскольку «голое» решение могут и забраковать.
Следующее тело для самостоятельного дела:
Пример 2
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями
![]()
В данном случае область интегрирования задана преимущественно неравенствами, и это даже лучше – множество неравенств ![]() задаёт 1-й октант, включая координатные плоскости, а неравенство
задаёт 1-й октант, включая координатные плоскости, а неравенство ![]() – полупространство, содержащее начало координат (проверьте) + саму плоскость. «Вертикальная» плоскость
– полупространство, содержащее начало координат (проверьте) + саму плоскость. «Вертикальная» плоскость ![]() рассекает параболоид по параболе и на чертеже желательно построить данное сечение. Для этого нужно найти дополнительную опорную точку, проще всего – вершину параболы (рассматриваем значения
рассекает параболоид по параболе и на чертеже желательно построить данное сечение. Для этого нужно найти дополнительную опорную точку, проще всего – вершину параболы (рассматриваем значения ![]() и рассчитываем соответствующее «зет»).
и рассчитываем соответствующее «зет»).
Примерный образец оформления задачи в конце урока.
Продолжаем разминаться:
Пример 3
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Выполнить чертёж.
![]()
Решение: формулировка «выполнить чертёж» даёт нам некоторую свободу, но, скорее всего, подразумевает выполнение пространственного чертежа. Однако и проекция тоже не помешает, тем более, она здесь не самая простая.
Придерживаемся отработанной ранее тактики – сначала разберёмся с поверхностями, которые параллельны оси аппликат. Уравнения таких поверхностей не содержат в явном виде переменную «зет»:
– уравнение ![]() задаёт координатную плоскость
задаёт координатную плоскость ![]() , проходящую через ось
, проходящую через ось ![]() (которая на плоскости
(которая на плоскости ![]() определяется «одноимённым» уравнением
определяется «одноимённым» уравнением ![]() );
);
– уравнение ![]() задаёт плоскость, проходящую через «одноимённую» «плоскую» прямую параллельно оси
задаёт плоскость, проходящую через «одноимённую» «плоскую» прямую параллельно оси ![]() .
.
Но две прямые ![]() не задают ограниченную проекцию, и, очевидно, её должны «прорисовать» линии, по которым параболический цилиндр
не задают ограниченную проекцию, и, очевидно, её должны «прорисовать» линии, по которым параболический цилиндр ![]() пересекает плоскость
пересекает плоскость ![]() . Чтобы найти уравнения этих линий нужно решить простейшую систему:
. Чтобы найти уравнения этих линий нужно решить простейшую систему:
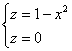
Подставим ![]() в первое уравнение:
в первое уравнение:
![]() – получены две прямые, лежащие в плоскости
– получены две прямые, лежащие в плоскости ![]() , параллельные оси
, параллельные оси ![]() .
.
Изобразим проекцию тела на плоскость ![]() :
:
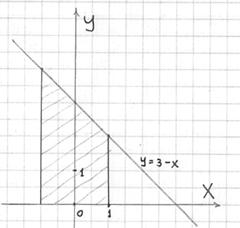
Ещё раз призываю! – если остаётся какое-то недопонимание по выполнению чертежей и/или объяснениям, обращайтесь к справочной статье Основные поверхности пространства и в тяжёлом случае – к урокам Уравнение прямой на плоскости, Уравнение плоскости.
Искомое тело ограниченно плоскостью ![]() снизу и параболическим цилиндром
снизу и параболическим цилиндром ![]() сверху:
сверху:
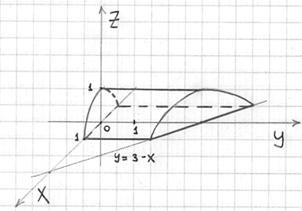
Составим порядок обхода тела, при этом «иксовые» и «игрековые» пределы интегрирования, напоминаю, удобнее выяснять по двумерному чертежу:
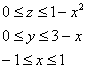
Таким образом:
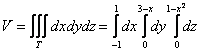
1) 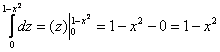
2) 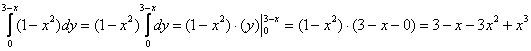
При интегрировании по «игрек» – «икс» считается константой, поэтому константу ![]() целесообразно сразу вынести за знак интеграла.
целесообразно сразу вынести за знак интеграла.
3)
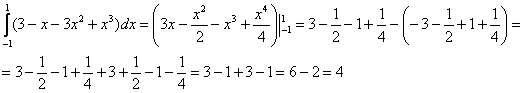
Ответ: ![]()
Да, чуть не забыл, в большинстве случаев полученный результат малополезно (и даже вредно) сверять с трёхмерным чертежом, поскольку с большой вероятностью возникнет иллюзия объёма, о которой я рассказал ещё на уроке Объем тела вращения. Так, оценивая тело рассмотренной задачи, лично мне показалось, что в нём гораздо больше 4 «кубиков».
Следующий пример для самостоятельного решения:
Пример 4
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость ![]() .
.
![]()
Примерный образец оформления задачи в конце урока.
Не редкость, когда выполнение трёхмерного чертежа затруднено:
Пример 5
С помощью тройного интеграла найти объём тела, заданного ограничивающими его поверхностями
![]()
Решение: проекция здесь несложная, но вот над порядком её обхода нужно подумать. Если выбрать 1-й способ, то фигуру придётся разделить на 2 части, что неиллюзорно грозит вычислением суммы двух тройных интегралов. В этой связи гораздо перспективнее выглядит 2-й путь. Выразим ![]() и изобразим проекцию данного тела на чертеже:
и изобразим проекцию данного тела на чертеже:
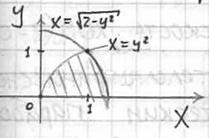
Прошу прощения за качество некоторых картинок, я их вырезаю прямо из собственных рукописей.
Выбираем более выгодный порядок обхода фигуры:
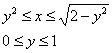
Теперь дело за телом. Снизу оно ограничено плоскостью ![]() , сверху – плоскостью
, сверху – плоскостью ![]() , которая проходит через ось ординат. И всё бы было ничего, но последняя плоскость слишком крутА и построить область не так-то просто. Выбор тут незавиден: либо ювелирная работа в мелком масштабе (т.к. тело достаточно тонкое), либо чертёж высотой порядка 20 сантиметров (да и то, если вместится).
, которая проходит через ось ординат. И всё бы было ничего, но последняя плоскость слишком крутА и построить область не так-то просто. Выбор тут незавиден: либо ювелирная работа в мелком масштабе (т.к. тело достаточно тонкое), либо чертёж высотой порядка 20 сантиметров (да и то, если вместится).
Но есть третий, исконно русский метод решения проблемы – забить =) И вместо трёхмерного чертежа обойтись словесным описанием: «Данное тело ограничено цилиндрами ![]() и плоскостью
и плоскостью ![]() сбоку, плоскостью
сбоку, плоскостью ![]() – снизу и плоскостью
– снизу и плоскостью ![]() – сверху».
– сверху».
«Вертикальные» пределы интегрирования, очевидно, таковы: ![]()
Вычислим объём тела, не забывая, что проекцию мы обошли менее распространённым способом:
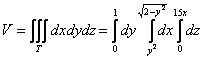
1) 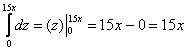
2) 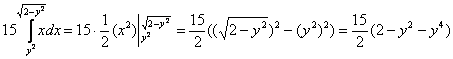
3) 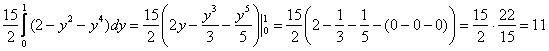
Ответ: ![]()
Как вы заметили, предлагаемые в задачах тела не дороже сотни баксов часто ограничены плоскостью ![]() снизу. Но это не есть какое-то правило, поэтому всегда нужно быть начеку – может попасться задание, где тело расположено и под плоскостью
снизу. Но это не есть какое-то правило, поэтому всегда нужно быть начеку – может попасться задание, где тело расположено и под плоскостью ![]() . Так, например, если в разобранной задаче вместо
. Так, например, если в разобранной задаче вместо ![]() рассмотреть плоскость
рассмотреть плоскость ![]() , то исследованное тело симметрично отобразится в нижнее полупространство и будет ограничено плоскостью
, то исследованное тело симметрично отобразится в нижнее полупространство и будет ограничено плоскостью ![]() снизу, а плоскостью
снизу, а плоскостью ![]() – уже сверху!
– уже сверху!
Легко убедиться, что получится тот же самый результат:
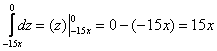
(помним, что тело нужно обходить строго снизу вверх!)
Кроме того, «любимая» плоскость может оказаться вообще не при делах, простейший пример: шар, расположенный выше плоскости ![]() – при вычислении его объёма уравнение
– при вычислении его объёма уравнение ![]() не понадобится вообще.
не понадобится вообще.
Все эти случаи мы рассмотрим, а пока аналогичное задание для самостоятельного решения:
Пример 6
С помощью тройного интеграла найти объём тела, ограниченного поверхностями
![]()
Краткое решение и ответ в конце урока.
Переходим ко второму параграфу с не менее популярными материалами:
Тройной интеграл в цилиндрических координатах
Цилиндрические координаты – это, по сути, полярные координаты в пространстве.
В цилиндрической системе координат положение точки ![]() пространства определяется полярными координатами
пространства определяется полярными координатами ![]() и
и ![]() точки
точки ![]() – проекции точки
– проекции точки ![]() на плоскость
на плоскость ![]() и аппликатой
и аппликатой ![]() самой точки
самой точки ![]() .
.
Переход от трёхмерной декартовой системы к цилиндрической системе координат осуществляется по следующим формулам:

Применительно к нашей теме преобразование выглядит следующим образом:
![]()
И, соответственно, в упрощённом случае, который мы рассматриваем в этой статье:
![]()
Главное, не забывать про дополнительный множитель «эр» и правильно расставлять полярные пределы интегрирования при обходе проекции:
Пример 7
Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями ![]() . Выполнить чертежи данного тела и его проекции на плоскость
. Выполнить чертежи данного тела и его проекции на плоскость ![]() .
.
Решение: придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых отсутствует переменная «зет». Оно здесь одно. Проекция цилиндрической поверхности ![]() на плоскость
на плоскость ![]() представляет собой «одноимённую» окружность
представляет собой «одноимённую» окружность ![]() .
.
Плоскости ![]() ограничивают искомое тело снизу и сверху («высекают» его из цилиндра) и проецируются в круг
ограничивают искомое тело снизу и сверху («высекают» его из цилиндра) и проецируются в круг ![]() :
:
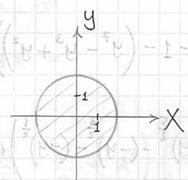
На очереди трёхмерный чертёж. Основная трудность состоит в построении плоскости ![]() , которая пересекает цилиндр
, которая пересекает цилиндр ![]() под «косым» углом, в результате чего получается эллипс. Уточним данное сечение аналитически: для этого перепишем уравнение плоскости в функциональном виде
под «косым» углом, в результате чего получается эллипс. Уточним данное сечение аналитически: для этого перепишем уравнение плоскости в функциональном виде ![]() и вычислим значения функции («высоту») в напрашивающихся точках
и вычислим значения функции («высоту») в напрашивающихся точках ![]() , которые лежат на границе проекции:
, которые лежат на границе проекции:
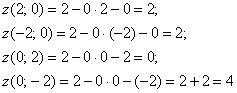
Отмечаем найденные точки на чертеже и аккуратно (а не так, как я =)) соединяем их линией:
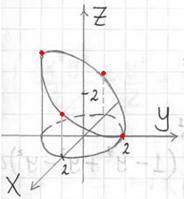
Проекция тела на плоскость ![]() представляет собой круг, и это весомый аргумент в пользу перехода к цилиндрической системе координат:
представляет собой круг, и это весомый аргумент в пользу перехода к цилиндрической системе координат:
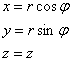
Найдём уравнения поверхностей в цилиндрических координатах:
![]()
Теперь следует выяснить порядок обхода тела.
Сначала разберёмся с проекцией. Как определить её порядок обхода? ТОЧНО ТАК ЖЕ, как и при вычислении двойных интегралов в полярных координатах. Здесь он элементарен:
![]()
«Вертикальные» пределы интегрирования тоже очевидны – входим в тело через плоскость ![]() и выходим из него через плоскость
и выходим из него через плоскость ![]() :
:
![]()
Перейдём к повторным интегралам:
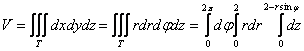
При этом множитель «эр» сразу ставим в «свой» интеграл.
Веник как обычно легче сломать по прутикам:
1) 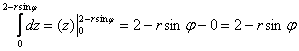
Сносим результат в следующий интеграл:
2) 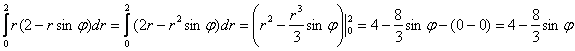
А тут не забываем, что «фи» считается константой. Но это до поры до времени:
3) 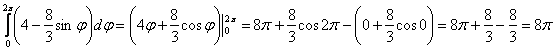
Ответ: ![]()
Похожее задание для самостоятельного решения:
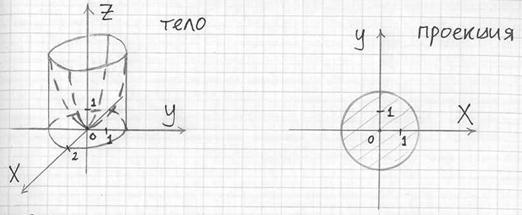
Пример 8
Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями ![]() . Выполнить чертежи данного тела и его проекции на плоскость
. Выполнить чертежи данного тела и его проекции на плоскость ![]() .
.
Примерный образец чистового оформления в конце урока.
Обратите внимание, что в условиях задач ни слова не сказано о переходе к цилиндрической системе координат, и несведущий человек будет бодаться с трудными интегралами в декартовых координатах. …А может и не будет – ведь есть третий, исконно русский способ решения проблем =)
Всё только начинается! …в хорошем смысле: =)
Пример 9
С помощью тройного интеграла найти объем тела, ограниченного поверхностями ![]()
Скромно и со вкусом.
Решение: данное тело ограничено конической поверхностью ![]() и эллиптическим параболоидом
и эллиптическим параболоидом ![]() . Читатели, которые внимательно ознакомились с материалами статьи Основные поверхности пространства, уже представили, как выглядит тело, но на практике часто встречаются более сложные случаи, поэтому я проведу подробное аналитическое рассуждение.
. Читатели, которые внимательно ознакомились с материалами статьи Основные поверхности пространства, уже представили, как выглядит тело, но на практике часто встречаются более сложные случаи, поэтому я проведу подробное аналитическое рассуждение.
Сначала найдём линии, по которым пересекаются поверхности. Составим и решим следующую систему:
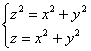
Из 1-го уравнения почленно вычтем второе:
![]()
В результате получено два корня: ![]()
Подставим найденное значение ![]() в любое уравнение системы:
в любое уравнение системы:
![]() , откуда следует, что
, откуда следует, что ![]()
Таким образом, корню ![]() соответствует единственная точка – начало координат. Естественно – ведь вершины рассматриваемых поверхностей совпадают.
соответствует единственная точка – начало координат. Естественно – ведь вершины рассматриваемых поверхностей совпадают.
Теперь подставим второй корень ![]() – тоже в любое уравнение системы:
– тоже в любое уравнение системы:
![]()
Каков геометрический смысл полученного результата? «На высоте» ![]() (в плоскости
(в плоскости ![]() ) параболоид и конус пересекаются по окружности
) параболоид и конус пересекаются по окружности ![]() – единичного радиуса с центром в точке
– единичного радиуса с центром в точке ![]() .
.
При этом «чаша» параболоида вмещает в себя «воронку» конуса, поэтому образующие конической поверхности следует прочертить пунктиром (за исключением отрезка дальней от нас образующей, который виден с данного ракурса):
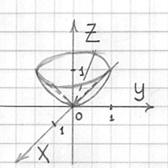
Проекцией тела на плоскость ![]() является круг
является круг ![]() с центром в начале координат радиуса 1, который я даже не удосужился изобразить ввиду очевидности данного факта (однако письменный комментарий делаем!). Кстати, в двух предыдущих задачах на чертёж проекции тоже можно было бы забить, если бы не условие.
с центром в начале координат радиуса 1, который я даже не удосужился изобразить ввиду очевидности данного факта (однако письменный комментарий делаем!). Кстати, в двух предыдущих задачах на чертёж проекции тоже можно было бы забить, если бы не условие.
При переходе к цилиндрическим координатам по стандартным формулам неравенство запишется в простейшем виде ![]() и с порядком обхода проекции никаких проблем:
и с порядком обхода проекции никаких проблем:
![]()
Найдём уравнения поверхностей в цилиндрической системе координат:
![]()
Так как в задаче рассматривается верхняя часть конуса, то из уравнения ![]() выражаем:
выражаем:
![]()
«Сканируем тело» снизу вверх. Лучи света входят в него через эллиптический параболоид ![]() и выходят через коническую поверхность
и выходят через коническую поверхность ![]() . Таким образом, «вертикальный» порядок обхода тела:
. Таким образом, «вертикальный» порядок обхода тела:
![]()
Остальное дело техники:

Ответ: ![]()
Не редкость, когда тело задаётся не ограничивающими его поверхностями, а множеством неравенств:
Пример 10
С помощью тройного интеграла вычислить объём заданного тела:
![]() , где
, где ![]() – произвольное положительное число.
– произвольное положительное число.
Геометрический смысл пространственных неравенств я достаточно подробно разъяснил в той же справочной статье – Основные поверхности пространства и их построение.
Данная задача хоть и содержит параметр, но допускает выполнение точного чертежа, отражающего принципиальный вид тела. Подумайте, как выполнить построение. Краткое решение и ответ – в конце урока.
…ну что, ещё парочку заданий? Думал закончить урок, но прямо так и чувствую, что вы хотите ещё =)
Пример 11
С помощью тройного интеграла вычислить объём заданного тела:
![]() , где
, где ![]() – произвольное положительное число.
– произвольное положительное число.
Решение: неравенство ![]() задаёт шар с центром в начале координат радиуса
задаёт шар с центром в начале координат радиуса ![]() , а неравенство
, а неравенство ![]() – «внутренность» кругового цилиндра с осью симметрии
– «внутренность» кругового цилиндра с осью симметрии ![]() радиуса
радиуса ![]() . Таким образом, искомое тело ограничено круговым цилиндром сбоку и симметричными относительно плоскости
. Таким образом, искомое тело ограничено круговым цилиндром сбоку и симметричными относительно плоскости ![]() сферическими сегментами сверху и снизу.
сферическими сегментами сверху и снизу.
Принимая ![]() за базовую единицу измерения, выполним чертёж:
за базовую единицу измерения, выполним чертёж:
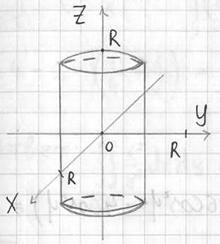
Точнее, его следует назвать рисунком, поскольку пропорции по оси ![]() я выдержал не очень-то хорошо. Однако, справедливости ради, по условию вообще не требовалось ничего чертить и такой иллюстрации оказалось вполне достаточно.
я выдержал не очень-то хорошо. Однако, справедливости ради, по условию вообще не требовалось ничего чертить и такой иллюстрации оказалось вполне достаточно.
Обратите внимание, что здесь не обязательно выяснять высоту, на которой цилиндр высекает из шара «шапки» – если взять в руки циркуль и наметить им окружность с центром в начале координат радиуса 2 см, то точки пересечения с цилиндром получатся сами собой.
Кстати, как найти эту высоту аналитически? Нужно подставить сумму квадратов ![]() в уравнение сферы
в уравнение сферы ![]() :
:
![]()
Но вернёмся к теме. Проекция данного тела на плоскость ![]() представляет собой круг с центром в начале координат радиуса
представляет собой круг с центром в начале координат радиуса ![]() (на чертеже отсутствует) и поэтому нас снова выручают цилиндрические координаты. Порядок обхода проекции тривиален:
(на чертеже отсутствует) и поэтому нас снова выручают цилиндрические координаты. Порядок обхода проекции тривиален:
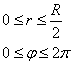
По формулам перехода ![]() найдём уравнение сферы в цилиндрических координатах:
найдём уравнение сферы в цилиндрических координатах:
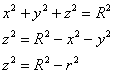
![]() – задаёт верхнюю полусферу;
– задаёт верхнюю полусферу;
![]() – задаёт нижнюю полусферу.
– задаёт нижнюю полусферу.
Лучи «лазера» входят в тело через нижнюю «шапку» и выходят через верхнюю, таким образом:
![]()
Можно сослаться на симметрию и вычислить объём половины тела, но, как ни странно, это только заморочит решение – гораздо проще провести формальные вычисления.
Расписываем и щёлкаем повторные интегралы:
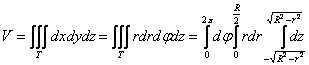
1) 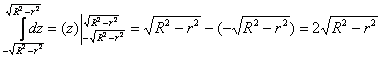
Вот так – и никаких комментов о симметрии. Сносим результат в следующий интеграл:
2)
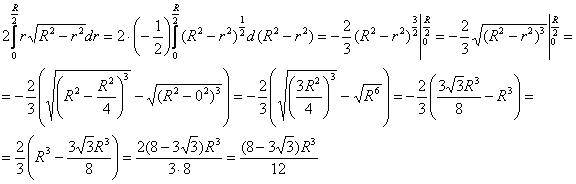
Здесь в целях сократить решение я подвёл функцию под знак дифференциала, но «чайникам» всё же рекомендую «классический» путь замены переменной.
Сносим полученную константу в последний интеграл, а точнее, сразу выносим её за его пределы:
3) 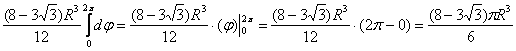
Ответ: ![]()
Косвенным признаком правильности вычислений является тот факт, что параметр вошёл в ответ в кубе. Ну и ещё на всякий пожарный, проверим, не получился ли случаем результат отрицательным: ![]() – нет, не получился. Хотя всё это, конечно, нельзя считать надёжной проверкой.
– нет, не получился. Хотя всё это, конечно, нельзя считать надёжной проверкой.
Заключительное задание для самостоятельного решения:
Пример 12
С помощью тройного интеграла вычислить объём тела, ограниченного поверхностями
![]()
Особенность этого примера состоит в том, что здесь затруднено построение трёхмерного чертежа (уже знакомый из предыдущего параграфа мотив) и в этой связи тело придётся представить мысленно. Да и проекция, к слову, тоже не сахар.
В данную статью я включил не самые сложные примеры, и желающие могут закачать дополнительные задачи с готовыми решениями, в частности, интересны и поучительны примеры, где тело приходится разделять на 2 части.
Ну а сейчас я предлагаю сделать передышку и ознакомиться с заключительной частью урока – Как вычислить произвольный тройной интеграл?
Решения и ответы:
Пример 2: Решение: изобразим данное тело на чертеже.
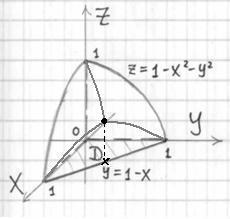
Примечание: при ![]() (чёрный крестик)
(чёрный крестик) ![]() (чёрная точка – вершина параболы).
(чёрная точка – вершина параболы).
Порядок обхода тела:
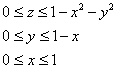
Объём тела вычислим с помощью тройного интеграла:

Ответ: ![]()
Пример 4: Решение: изобразим проекцию данного тела на плоскость ![]() :
:
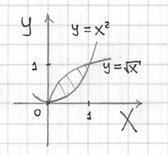
Данное тело ограничено параболическими цилиндрами сбоку, плоскостью ![]() – снизу и плоскостью
– снизу и плоскостью ![]() – сверху (последнюю лучше всего изобразить в отрезках):
– сверху (последнюю лучше всего изобразить в отрезках):
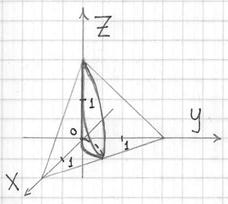
Выберем следующий порядок обхода тела:
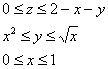
Таким образом:

Ответ: ![]()
Пример 6: Решение: изобразим проекцию данного тела на плоскость ![]() :
:
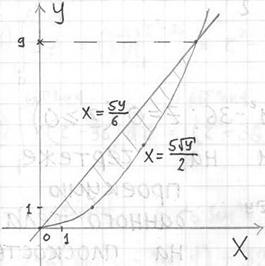
Данное тело ограничено параболическим цилиндром ![]() и плоскостью
и плоскостью ![]() сбоку, плоскостью
сбоку, плоскостью ![]() – снизу и параболическим цилиндром
– снизу и параболическим цилиндром ![]() – сверху.
– сверху.
Примечание: обратите внимание, что ![]() при любых
при любых ![]() , т.е. данная поверхность лежит выше координатной плоскости
, т.е. данная поверхность лежит выше координатной плоскости ![]() .
.
Выберем следующий порядок обхода тела:
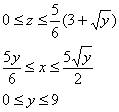
Вычислим объём тела:

Ответ: ![]()
Пример 8: Решение: данное тело ограничено плоскостью ![]() снизу, эллиптическим параболоидом
снизу, эллиптическим параболоидом ![]() – сверху и цилиндром
– сверху и цилиндром ![]() – сбоку. Выполним чертежи:
– сбоку. Выполним чертежи:
Объём тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат:
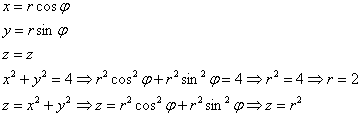
Порядок обхода тела:
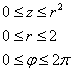
Таким образом:
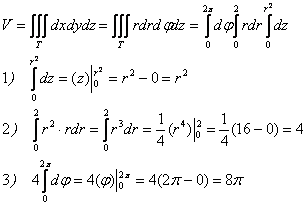
Ответ: ![]()
Пример 10: Решение: данное тело ограничено плоскостью ![]() снизу, сферой
снизу, сферой ![]() – сверху и цилиндрической поверхностью
– сверху и цилиндрической поверхностью ![]() – изнутри:
– изнутри:
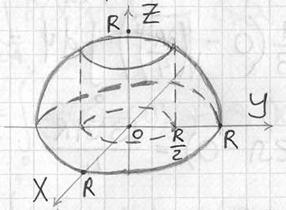
Проекция тела на плоскость ![]() представляет собой кольцо с внутренним радиусом
представляет собой кольцо с внутренним радиусом ![]() и внешним радиусом
и внешним радиусом ![]() . Объём тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат:
. Объём тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат:
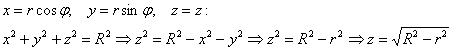 :
:
Порядок обхода тела:
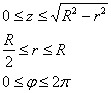
Таким образом:

Ответ: ![]()
Пример 12: Решение: изобразим проекцию данного тела на плоскость ![]() . Сначала преобразуем уравнение:
. Сначала преобразуем уравнение: ![]() .
.
Проекцией цилиндра ![]() является окружность с центром в точке
является окружность с центром в точке ![]() радиуса
радиуса ![]() .
.
Найдём линию пересечения эллиптического параболоида с плоскостью ![]() :
:
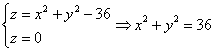 – окружность с центром в начале координат радиуса 6.
– окружность с центром в начале координат радиуса 6.
Выполним чертёж:
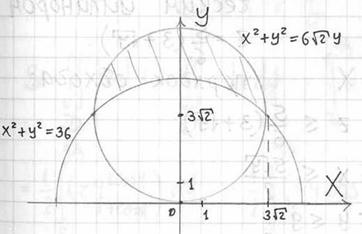
Искомое тело ограничено плоскостью ![]() снизу, эллиптическим параболоидом
снизу, эллиптическим параболоидом ![]() – сверху и цилиндрической поверхностью
– сверху и цилиндрической поверхностью ![]() – сбоку.
– сбоку.
Объём тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат:
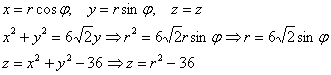
Порядок обхода тела:
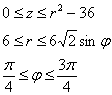
Таким образом:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright